- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Перевод чисел
Содержание
Слайд 2
ВЫВОД АЛГОРИТМА ПЕРЕВОДА
Разложим целое десятичное число Ацл в ряд
Получим запись в развернутой форме двоичного целого числа, так как в этой записи отсутствуют отрицательные степени основания, т.е. числа 2:
На первом шаге разделим число Ацл на основание двоичной системы, т.е. на 2.
Частное от деления будет равно: ,
а остаток равен .
На втором шаге целое частное опять разделим на 2, остаток от деления будет равен .
После n-го шага получим последовательность остатков: ,
которая совпадает с обратной последовательностью цифр
целого двоичного числа, записанного в свернутой форме:
Чтобы получить искомое двоичное число, достаточно
записать остатки в обратной последовательности.
Аналогичные рассуждения могут быть проведены и для перевода целых десятичных чисел в восьмеричную и шестнадцатеричную системы счисления.
Слайд 3
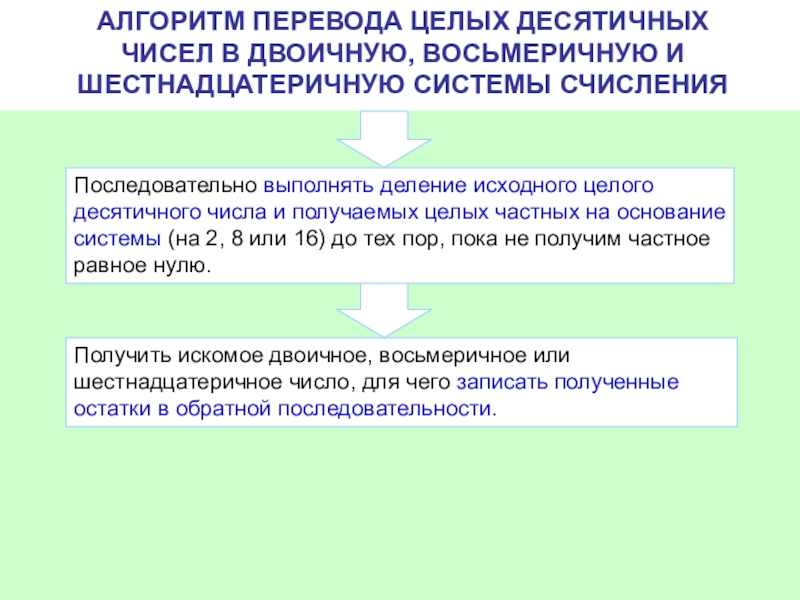
АЛГОРИТМ ПЕРЕВОДА ЦЕЛЫХ ДЕСЯТИЧНЫХ ЧИСЕЛ В ДВОИЧНУЮ, ВОСЬМЕРИЧНУЮ И ШЕСТНАДЦАТЕРИЧНУЮ СИСТЕМЫ
Получить искомое двоичное, восьмеричное или шестнадцатеричное число, для чего записать полученные остатки в обратной последовательности.
Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2, 8 или 16) до тех пор, пока не получим частное равное нулю.
Слайд 4
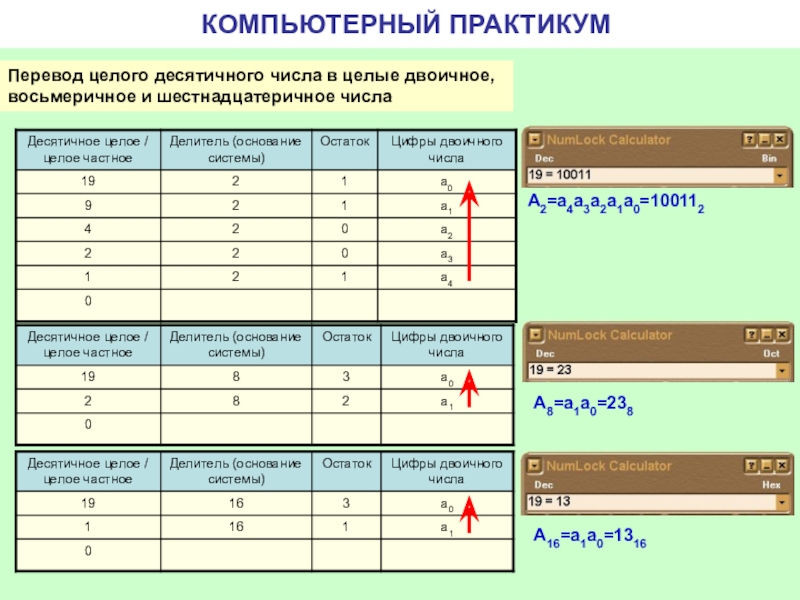
КОМПЬЮТЕРНЫЙ ПРАКТИКУМ
Перевод целого десятичного числа в целые двоичное, восьмеричное и шестнадцатеричное
А2=а4а3а2а1а0=100112
А8=а1а0=238
А16=а1а0=1316