- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Основы дискретной математики
Содержание
- 1. Основы дискретной математики
- 2. “Теперь в математике остаются
- 3. Основное отличие дискретной математики от классической заключается
- 4. Тема:Основы дискретной математики
- 5. Цель: Цель:Рассмотреть основные понятия множества, основ логики, теории графов.
- 6. Задачи Лекции:1 Дать определение множеств, отношений и
- 7. План Лекции:1. Функции, отношения и множества 2. Основы логики 3. Графы и деревья
- 8. I. Функции, отношения и множества
- 9. X и Y – некоторые числовые множества.
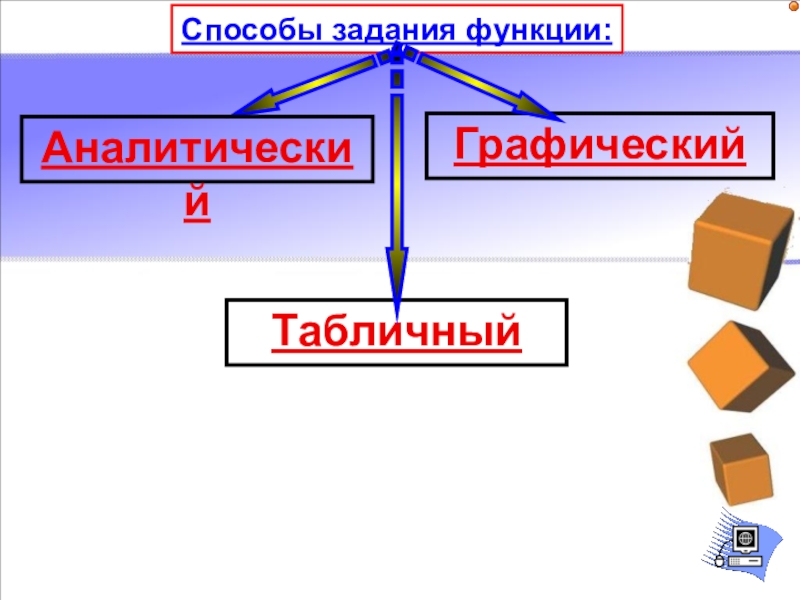
- 10. Способы задания функции:Аналитический Табличный Графический
- 11. Аналитический При аналитическом способе задания функция задается
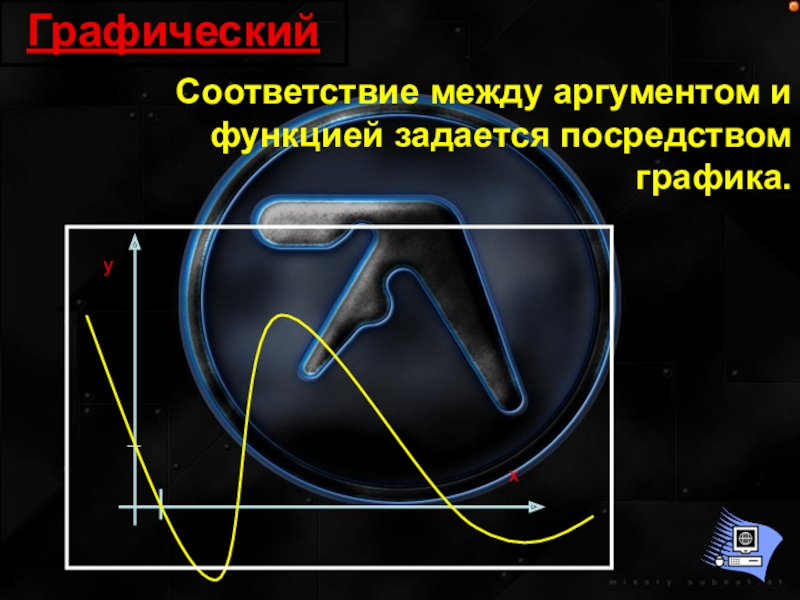
- 12. Графический Соответствие между аргументом и функцией задается посредством графика.уx
- 13. Табличный Данный способ формирует соответствие между аргументом и функцией посредством табличных значений
- 14. Классификация элементарных функций Тригонометрическая:
- 15. Совокупность каких-либо объектов, обладающих общими свойствами, называют
- 16. “∈“ “∉“ Например: x∈A Например: х∉A Принадлежность
- 17. Понятие множестваСчетное - Множество, каждый элемент которого
- 18. Если все элементы множества A являются также
- 19. Пустое и универсальное множествоМножество, не содержащее ни
- 20. Множество, элементами которого являются подмножества, называют семейством
- 21. Алгебра множеств Функции, область определения и область
- 22. Законы алгебры множеств Коммутативности: (A∪B)=(B∪A) и (A∩B)=(B∩A);Ассоциативности:
- 23. Объединение множеств А и В есть множество,
- 24. Пересечение множеств А и В есть множество,
- 25. Обозначение:Разность множествРазность множеств А и В есть
- 26. Обозначение:Симметрическая Разность множествСимметрическая разность множеств А и
- 27. Отображение, заданное между элементами одного множества Х,
- 28. Бинарным или двуместным отношением между элементами множеств
- 29. Симметричность Антисимметричность Асимметричность Транзитивность Антирефлексивность Свойства отношенийСвойства отношений Рефлексивность
- 30. Бинарное отношение рефликсивно, если для каждого хi∈Х
- 31. Антисимметричность Бинарное отношение антисимметрично, если для любой
- 32. Симметричность Бинарное отношение симметрично, если для любой
- 33. Антирефлексивность Бинарное отношение антирефлексивно, если для каждого
- 34. Транзитивность Бинарное отношение транзитивно, если для любых
- 35. Асимметричность Бинарное отношение асимметрично, если
- 36. Бинарное отношение, удовлетворяющее условиям рефлексивности, симметричности и
- 37. II. Основы логики
- 38. Первые учения о формах и способах рассуждений
- 39. Вильгельм Готфрид Лейбниц (1646 - 1716)Второй этап
- 40. Джордж Буль (1815-1864) Основоположник математической логики считается
- 41. В современное время для анализа и синтеза
- 42. Алгебра логики – это раздел математики, изучающий
- 43. Типы формальных систем Логика высказываний Логика предикатов Логика отношений Нечеткая логика
- 44. Логика предикатов Логика предикатов (predicate calculus) есть
- 45. Логика высказываний Логика высказываний (prepositional calculus) есть
- 46. Нечеткая логика Логика нечеткая (fuzzi calculus) есть
- 47. Логика отношений Логика отношений (relation calculus) есть
- 48. Любое повествовательное предложение, которое может быть признано
- 49. Алгебра высказываний Модель алгебры высказываний. Множество T={A,
- 50. Логические операцииЛогические операции бывают унарные (или одноместные)
- 51. ОтрицаниеЛогические операцииКонъюнкцияДизъюнкция ИмпликацияЭквиваленция
- 52. ОтрицаниеОтрицание (операция НЕ) есть одноместная операция, посредством
- 53. КонъюнкцияКонъюнкция есть двухместная операция, посредством которой из
- 54. Дизъюнкция есть двухместная операция, посредством которой из
- 55. ЭквиваленцияТаблица логической эквивалентности Обозначение:Эквиваленция есть двухместная операция,
- 56. Импликация есть двуместная операция, посредством которой отражающую
- 57. Законы Алгебры Логики Законы Алгебры Логики
- 58. III.Графы и деревья
- 59. Теория графов находит самое широкое применение в
- 60. Первая работа по теории графов была опубликована
- 61. Совокупность объектов произвольной природы и отношений между
- 62. Вершинами графа могут быть операторы программы или
- 63. Ориентированный граф - это пара (V, E),
- 64. Неориентированный граф G=(V, E) - это ориентированный
- 65. Деревья Деревья являются одним из интереснейших классов
- 66. Способы обхода деревьев. Часто при обработке представленной
- 67. Литература:1.Информатика Учеб. для студентов эконом. спец. вузов/под
- 68. ???Контрольные вопросы:Что такое множества?Что такое функция?Какие существуют
- 69. Спасибо За Внимание!!!
Слайд 1Костанайский Государственный Университет
им. Ахмета Байтурсынова
Автор презентации: ст. преподаватель кафедры ИиМ
Ермагамбетова Гульмира Нурлановна
Слайд 2“Теперь в математике остаются
системы целых чисел...”
Анри Пуанкаре.
Слайд 3Основное отличие дискретной математики от классической заключается в отсутствии понятия бесконечности,
В свою очередь, эти отношения изменяются в дискретные моменты времени.
Слайд 6Задачи Лекции:
1 Дать определение множеств, отношений и функций
2 Рассмотреть способы задания
3 Классифицировать функции
4 Рассмотреть основные понятия графов
5 Классифицировать основные логические операции
6 Изучить основные понятия о деревьях
Слайд 9
X и Y – некоторые числовые множества.
Если каждому элементу множества
Обозначение: f : x →y; y = f(x)
Здесь Y – зависимая переменная, X – независимая переменная (аргумент)
Понятие функции
Слайд 11Аналитический
При аналитическом способе задания функция задается с помощью формул:
Функция разрешена относительно y : y = х2
В неявном виде
Функция не разрешена относительно y: F(x,y) = 0
При аналитическом способе функцию можно задать:
Несколькими выражениями
Параметрически
В полярной системе координат
Слайд 13
Табличный
Данный способ формирует соответствие между аргументом и функцией посредством табличных
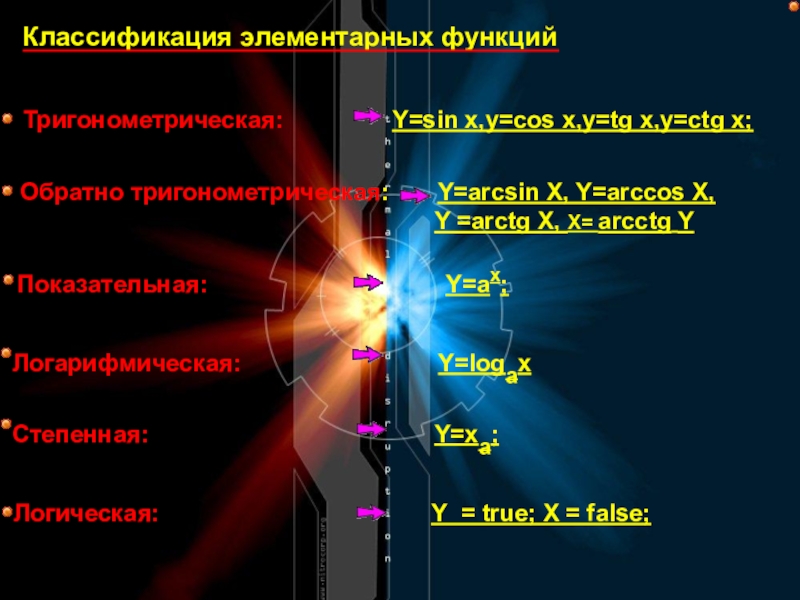
Слайд 14Классификация элементарных функций
Тригонометрическая:
Обратно тригонометрическая: Y=arcsin X, Y=arccos X,
Y =arctg X, X= arcctg Y
Степенная: Y=xa;
Показательная: Y=ax;
Логарифмическая: Y=logax
Логическая: Y = true; X = false;
Слайд 15Совокупность каких-либо объектов, обладающих общими свойствами, называют Множеством.
Понятие множества
Обозначение:
перечисляют элементы множества.
Например: {1, 3, 5, 7} или {a, b, c, d}.
Для обозначения множества в тексте используют прописные буквы латинского алфавита A, B, C, ...X, Y, Z, а для его элементов - строчные буквы a, b, c,...x, y, z.
Иногда эти буквы используют с индексами.
Слайд 16“∈“
“∉“
Например: x∈A
Например: х∉A
Принадлежность элемента X множеству A
Принадлежность множества
Элемент Х не принадлежит множеству A
Основное отношение между элементами и множеством - это отношение принадлежности элемента множеству.
Слайд 17Понятие множества
Счетное - Множество, каждый элемент которого можно индексировать целым числом
Если N конечно, то множество называют конечным.
Число элементов счетного конечного множества A называют его мощностью и обозначают так:
|A|=n.
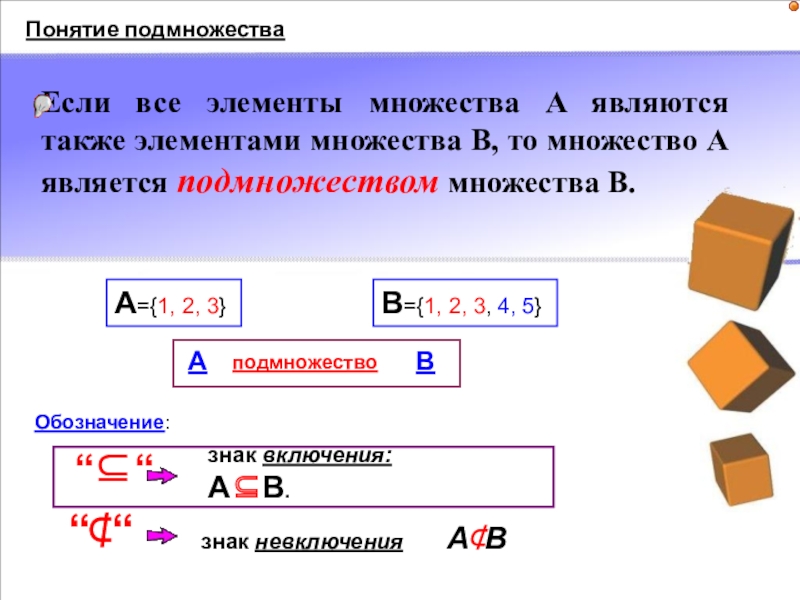
Слайд 18Если все элементы множества A являются также элементами множества B, то
Понятие подмножества
А={1, 2, 3}
B={1, 2, 3, 4, 5}
“⊆“
Обозначение:
знак включения: A⊆B.
знак невключения A⊄B
“⊄“
Слайд 19Пустое и универсальное множество
Множество, не содержащее ни одного элемента, называют пустым
Пустое множество является подмножеством любого множества.
Обозначение:
∅
Множество, содержащее все элементы всех подмножеств, принимающих участие в решении каких-либо задач, называют универсальным множеством.
∅ ={ } (нет элементов)
Обозначение:
U
U ={a, b, c, d}
Слайд 20Множество, элементами которого являются подмножества, называют семейством подмножеств.
Семейства и классы.
Множества, элементами которых являются другие множества, часто называют семействами или классами.
Например, A∈{{a, b}, {b, c, d}}, B∈{{a, b}, {b, c, d}}.
Максимально возможное число подмножеств универсального множества называют булеаном.
Булеан включает в себя пустое подмножество и множества, сформированные из одного, двух, трех и т.д. до общего числа элементов универсального множества.
Слайд 21Алгебра множеств
Функции, область определения и область значения которых принадлежит одному
fi: X→X или fi: Xn→X.
Множество X вместе c заданным множеством операций F={f1, f2, ..} называют Алгеброй.
Слайд 22Законы алгебры множеств
Коммутативности: (A∪B)=(B∪A) и (A∩B)=(B∩A);
Ассоциативности: A∪(B∪C)=(A∪B)∪C и
Идемпотентности: A∩A=A и A∪A=A;
Поглощения: A∩(A∪B)=A и A∪(A∩B)=A;
Дистрибутивности: A∪(B∩C)=(A∪B)∩(A∪C) и
A∩(B∪C)=(A∩B)∪(A∩C);
“Третьего не дано” A∪⎤A=U;
Противоречия: A∩⎤A=∅.
Двойного отрицания: ⎤ (⎤A)=A.
- символ унарной операции – дополнения,
∪ - символ бинарной операции – объединения,
∩ -символ бинарной операции - пересечения.
Слайд 23Объединение множеств А и В есть множество, состоящее из всех тех
Если В=∅, то А∪В=А∪∅=А.
Если B=U, то А∪В=А∪U=U.
Если А⊆С и В⊆С, то А∪В⊆С.
Обозначение:
Объединение множеств
Слайд 24Пересечение множеств А и В есть множество, состоящее из всех тех
Если В=∅, то А∩В=А∩∅=∅.
Если B=U, то А∩В=А∩U=А.
Если С⊆А и С⊆В, то С⊆А∩В.
Если А≠∅ и В≠∅, то при А∩В=∅ множества A и B не имеют общих элементов
Обозначение:
Пересечение множеств
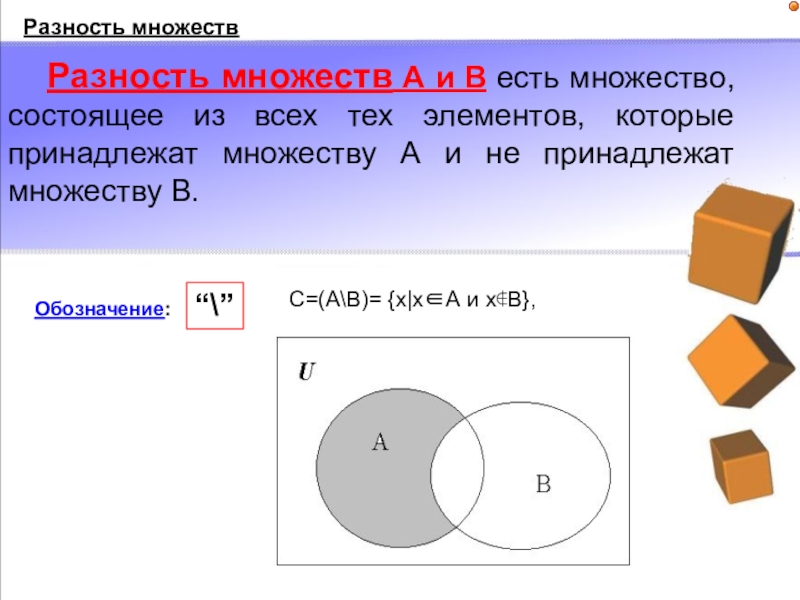
Слайд 25Обозначение:
Разность множеств
Разность множеств А и В есть множество, состоящее из всех
“\”
С=(А\В)= {x|x∈А и x∉В},
Слайд 26Обозначение:
Симметрическая Разность множеств
Симметрическая разность множеств А и В есть множество, состоящее
“Δ”
С=(АΔВ)=(А∩⎤В)∪(В∩⎤А)
(АΔВ)=(А∩⎤В)∪(В∩⎤А)=∅, то А=В.
*Это правило будет часто использоваться при доказательстве тождеств и поиске неизвестных множеств.
Слайд 27Отображение, заданное между элементами одного множества Х, называют Отношением.
Между математическими
Между “нематематическими” объектами
{“x принадлежит y”,
“x часть y”,
“x смежный y”,
“x родственник y”,
“x родитель y”, “x находится рядом с y”,..}.
Отношение
Слайд 28Бинарным или двуместным отношением между элементами множеств A и B называется
Говорят также, что R является отношением из A в B. При A = B отношение R называется бинарным отношением на A.
Вместо (x,y) R часто пишут xRy.)
R часто пишут xRy.
Бинарное отношение
Бинарные отношения между элементами множества X удобно описывать матрицами (Х⊗Х), строки и столбцы которых есть элементы множества.
На пересечении i-ой строки и j-го столбца ставят знак “1”, если задано отношение r(i, j) между i-м и j-м элементами и “0” в противном случае
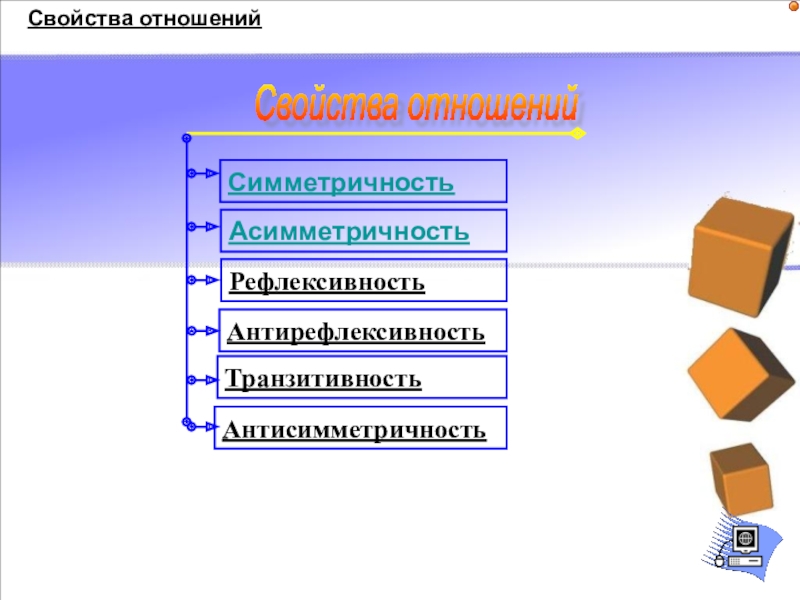
Слайд 29Симметричность
Антисимметричность
Асимметричность
Транзитивность
Антирефлексивность
Свойства отношений
Свойства отношений
Рефлексивность
Слайд 30Бинарное отношение рефликсивно, если для каждого хi∈Х имеем r(xi; xi)=1. Такими
При матричном описании такого отношения на главной диагонали матрицы будут только “1”, т.е. r(xi, xi)=1.
Рефлексивность
Слайд 31Антисимметричность
Бинарное отношение антисимметрично, если для любой пары (xi, xj) при
При матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали и наличие “1” на главной диагонали.
Слайд 32Симметричность
Бинарное отношение симметрично, если для любой пары (xi, xj)∈R имеем
При матричном задании такого отношения будет симметричное расположение “1” относительно главной диагонали, т.е. r(xi, xi)=r-1(xj, xi).
Слайд 33Антирефлексивность
Бинарное отношение антирефлексивно, если для каждого хi∈Х имеем r(xi, xi)=0.
При матричном описании такого отношения на главной диагонали матрицы будут только “0”, т.е. r(xi, xi)=0.
Слайд 34Транзитивность
Бинарное отношение транзитивно, если для любых элементов xi, xj, xk∈Х
Такими отношениями являются “..>..”, “..<..”, “быть родителем”, “быть родственником” и т.п..
Слайд 35Асимметричность
Бинарное отношение асимметрично, если для любой пары
Такими отношениями являются “.. > ..”, “..<..”, “быть родителем” и т.п.
При матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали и наличие “0” на главной диагонали.
Слайд 36Бинарное отношение, удовлетворяющее условиям рефлексивности, симметричности и транзитивности называют Отношением Эквиваленции.
Симметричность
Асимметричность
Рефлексивность
Отношения Эквиваленций
=
+
+
Отношения Эквиваленций
Отношение эквиваленции обозначают r~(xi, xi) или ~(xi, xi).
Слайд 38Первые учения о формах и способах рассуждений возникли в странах Древнего
История логики
Первым этапом на пути в развитии логики заложил Аристотель, создав основы формальной логики, где впервые отделил логические формы речи от ее содержания.
Слайд 39Вильгельм Готфрид Лейбниц (1646 - 1716)
Второй этап – математическая логика, основы
Слайд 40Джордж Буль (1815-1864)
Основоположник математической логики считается Джордж Буль (1815-1864),английский математик.
Поэтому начальный раздел математической логики часто называют булевой алгеброй или алгеброй логики.
Слайд 41В современное время для анализа и синтеза схем в ЭВМ при
Слайд 42Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны
Формальная система, носителем которой являются символы и последовательности символов формального языка, а множество операций используется для формирования и вывода новых суждений формального языка.
Математическая логика
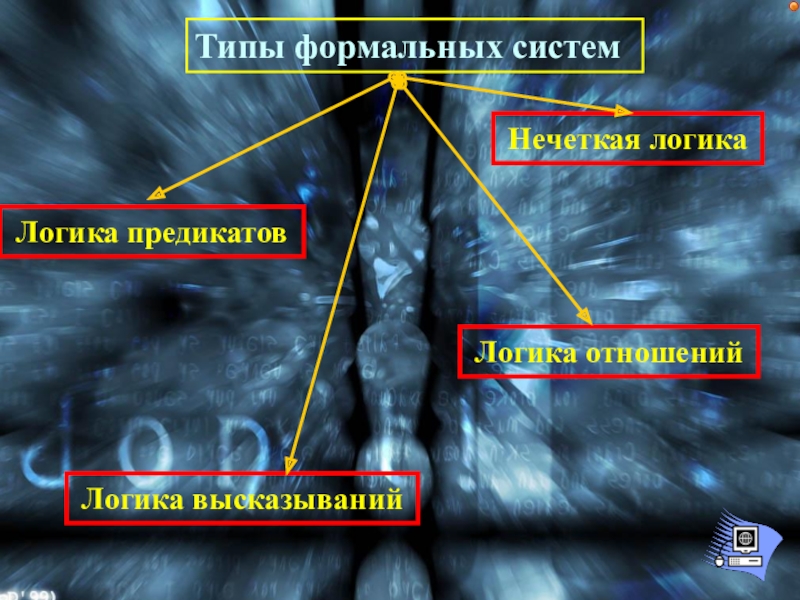
Слайд 43Типы формальных систем
Логика высказываний
Логика предикатов
Логика отношений
Нечеткая логика
Слайд 44Логика предикатов
Логика предикатов (predicate calculus) есть формальная система, предметом которой
Слайд 45Логика высказываний
Логика высказываний (prepositional calculus) есть модель формальной системы, предметом
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно сказать, истинно оно или ложно.
Например, предложение «6-четное число» следует считать высказыванием, так как оно истинное.
Предложение «Рим – столица Франции» тоже высказывание, так как оно ложное.
Слайд 46Нечеткая логика
Логика нечеткая (fuzzi calculus) есть формальная система, предметом которой
Слайд 47Логика отношений
Логика отношений (relation calculus) есть формальная система, предметом которой
Слайд 48Любое повествовательное предложение, которое может быть признано истинным или ложным, называют
Высказывания, которые получаются из простых предложений с помощью грамматических связок “не”, “и”, “или”, “если…, то…”, “… тогда и только тогда, когда…” и т.п., называют сложными.
Для обозначения грамматических связок в формальном языке вводят дополнительные символы, которые называют логическими связками.
∨:=”или”,
&:=“и”,
⎤:=”не”,
→:=“если…, то…”,
↔:=“…тогда и только тогда, когда …”.
Для построения сложных высказываний используют также вспомогательные символы “(“, “)” - скобки.
Высказывание
Слайд 49Алгебра высказываний
Модель алгебры высказываний. Множество T={A, B, C,…} с заданными
Сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических связок, называют формулой алгебры логики.
Слайд 50Логические операции
Логические операции бывают унарные (или одноместные) и бинарные (или двухместные).
Символы логических операций заданы логическими связками:
⎤ - отрицание,
& - конъюнкция,
∨ - дизъюнкция,
→ - импликация,
↔ - эквиваленция.
Различные значения логической формулы в зависимости от значений входящих в нее элементарных высказываний, могут быть полностью описаны с помощью таблицы истинности.
Слайд 52Отрицание
Отрицание (операция НЕ) есть одноместная операция, посредством которой ее значение есть
(⎤ F)
Обозначение:
Таблица логического отрицания
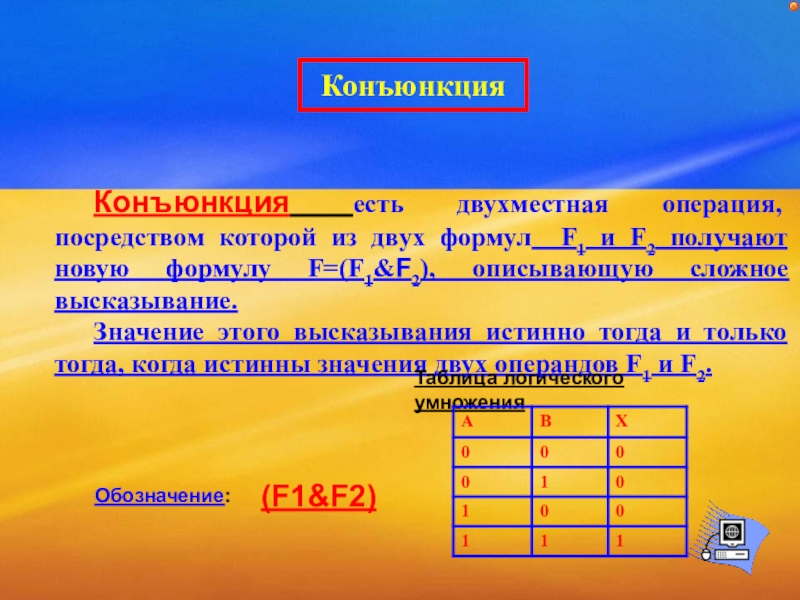
Слайд 53Конъюнкция
Конъюнкция есть двухместная операция, посредством которой из двух формул F1 и
Значение этого высказывания истинно тогда и только тогда, когда истинны значения двух операндов F1 и F2.
(F1&F2)
Обозначение:
Таблица логического умножения
Слайд 54Дизъюнкция есть двухместная операция, посредством которой из двух формул F1 и
Значение этого высказывания ложно тогда и только тогда, когда ложны значения двух операндов F1 или F2.
(F1∨F2)
Обозначение:
Дизъюнкция
Таблица логического сложения
Слайд 55Эквиваленция
Таблица логической эквивалентности
Обозначение:
Эквиваленция есть двухместная операция, посредством которой из двух
Значение этого высказывания истинно тогда и только тогда, когда оба операнда F1 и F2 имеют одинаковые значения.
(F1↔F2)
Слайд 56Импликация есть двуместная операция, посредством которой отражающую сложное высказывание. Значение этого
(F1→F2)
Обозначение:
Импликация
Таблица логического следования
Слайд 59Теория графов находит самое широкое применение в моделировании информационных процессов, в
Мы часто сталкиваемся с задачами, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи.
Если объекты изобразить точками (вершинами), а связи - линиями (ребрами), соединяющими соответствующие пары точек, то получится рисунок, называемый Графом.
Слайд 60Первая работа по теории графов была опубликована математиком Л. Эйлером в
Суть задачи сводилась к следующему: мог ли житель Кенигсберга, выйдя из дома, находящегося на части суши A, B, С или D, пройти по семи мостам через реку Прегель в точности по одному разу и вернуться домой?
Ответ на этот вопрос был отрицательным.
История графов
Для пояснения задачи представлена модель, где каждый участок суши замещен точкой на плоскости, а мосты – линиями, связывающими участки.
Слайд 61Совокупность объектов произвольной природы и отношений между каждой парой этих объектов
Множество точек, являющихся образом множества объектов, называют вершинами графа, а множество отрезков линий, являющихся образом множества отношений, - рёбрами или дугами графа.
Слайд 62Вершинами графа могут быть операторы программы или команды операционной системы, контактные
Рёбрами или дугами – связи операторов программы, команд операционной системы, контактных площадок на плате компьютера, узлов в транспортной или в электрической сети или причинно-следственные связи событий в любой сфере человеческой деятельности.
Вершина
Ребро
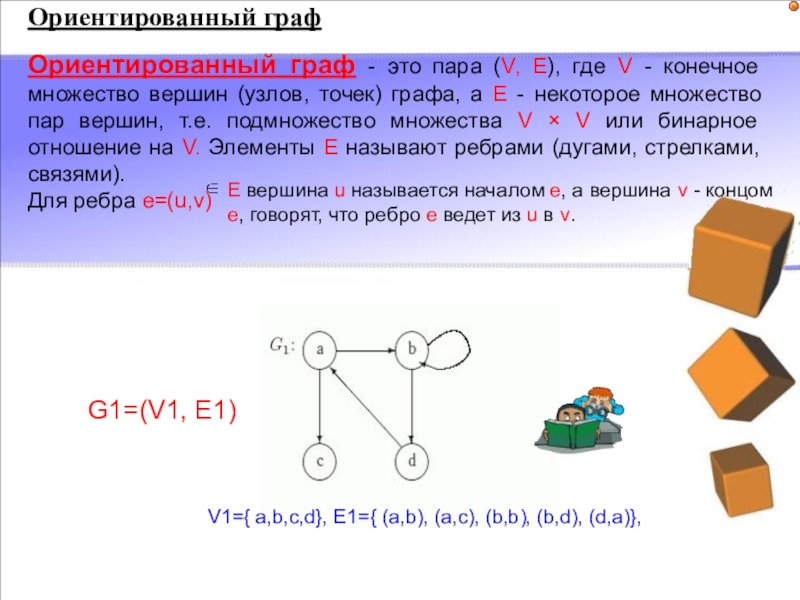
Слайд 63Ориентированный граф - это пара (V, E), где V - конечное
Для ребра e=(u,v)
E вершина u называется началом e, а вершина v - концом e, говорят, что ребро e ведет из u в v.
V1={ a,b,c,d}, E1={ (a,b), (a,c), (b,b), (b,d), (d,a)},
G1=(V1, E1)
Ориентированный граф
Слайд 64Неориентированный граф G=(V, E) - это ориентированный граф, у которого для
E имеется противоположное ребро (v,u) E,
т.е. отношение E симметрично.
Для его задания можно использовать обозначение для множества концов: {u, v}, но чаще используется указание одной из пар в круглых скобках. Если e= (u,v) E, то вершины u и v называются смежными в G, а ребро e и эти вершины называются инцидентными. Степенью вершины в неориентированном графе называется число смежных с ней вершин. Вершина степени 0 называется изолированной.
Такая пара (u,v), (v,u) называется неориентированным ребром
G2=(V2, E2 )
V2={ a,b,c,d}, E2={ (a,b), (a,c), (a,d), (b,d)}
Неориентированный граф
Слайд 65Деревья
Деревья являются одним из интереснейших классов графов, используемых для представления
Неориентированный граф называется деревом, если он связный и в нем нет циклов.
Ориентированный граф G=(V,E) называется (ориентированным) деревом, если:
в нем есть одна вершина, в которую не входят ребра; она называется корнем дерева
в каждую из остальных вершин входит ровно по одному ребру;
все вершины достижимы из корня.
Слайд 66Способы обхода деревьев.
Часто при обработке представленной в дереве информации требуется
Способы позволяют линейно упорядочить вершины дерева и тем самым представить его "двумерную структуру" в виде линейной последовательности вершин.
Способы обхода деревьев
Прямой
Обратный
основан на принципе: "сначала родитель, затем дети"
основан на противоположном принципе: "сначала дети, затем родитель".
Слайд 67Литература:
1.Информатика Учеб. для студентов эконом. спец. вузов/под ред.Макаровой.-3-е изд., - М.:
2.Угринович Н.Д. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений. Изд.2-е, испр.-М.: БИНОМ. Лаборатория знаний, 2004, с.84-108
3.Дехтярь М.И. Лекции по дискретной математике. БИНОМ. Лаборатория знаний, Интернет-университет информационных технологий - ИНТУИТ.ру, 2007
4.Алексеев В.Е., Таланов В.А. Графы и алгоритмы. Структуры данных. Модели вычислений. БИНОМ. Лаборатория знаний, Интернет-университет информационных технологий - ИНТУИТ.ру, 2006
5.Костюкова Н.И. Графы и их применение. Комбинаторные алгоритмы для программистов. БИНОМ. Лаборатория знаний, Интернет-университет информационных технологий - ИНТУИТ.ру, 2007
Слайд 68???
Контрольные вопросы:
Что такое множества?
Что такое функция?
Какие существуют функции?
Способы заданий функций?
Какие существуют
Что такое отношение?
Что такое математическая логика?
Перечислите логические операции?
Что такое графы?
Как представлены деревья?
Как классифицируются графы?