- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему : Алгоритмизация и программирование2
Содержание
- 1. : Алгоритмизация и программирование2
- 2. СодержаниеАлгоритм с итерационным циклом.Запоминание результатов.Типовые алгоритмы обработки одномерных массивов.Типовые алгоритмы обработки двумерных массивов.
- 3. Задача вычисления значений членов бесконечного рядас заданной точностью,...2! n!õ, ,...,x2 xnВычислить значения членов бесконечного ряда n!с точностью до члена рядаxn
- 4. Решение осуществляется в итерационном цикле, так как
- 5. Для вычисления текущего члена ряда в цикле
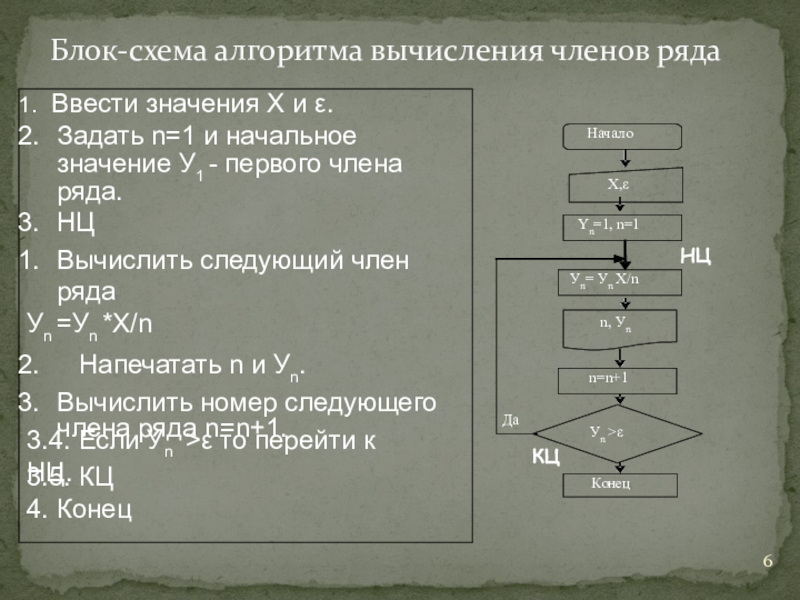
- 6. Блок-схема алгоритма вычисления членов рядаВвести значения Х
- 7. Запоминание результатовВ приведённых выше примерах результаты вычислений рассматривались
- 8. Запоминание результатовЕсли требуется сохранить в памяти (запомнить) все
- 9. Массив – это упорядоченная последовательность величин, обозначаемая
- 10. Номер элемента называется Индексом. Индексы в массиве
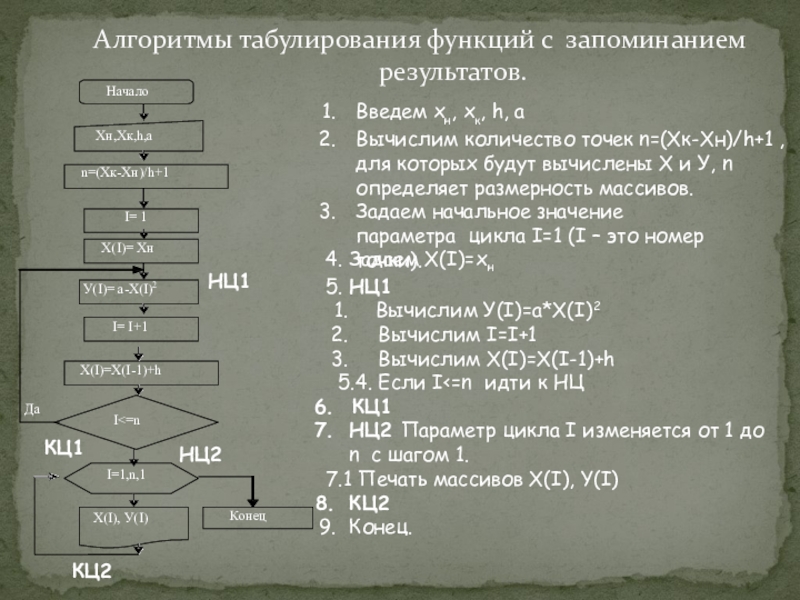
- 11. Алгоритмы табулирования функций с запоминанием результатов.У(I)= а-Х(I)2Х(I)=Х(I-1)+hНачалоХн,Хк,h,aДаI= 1I
- 12. сть 212Алгоритмы табулирования функций с использованием блока
- 13. 13Типовые алгоритмы обработки одномерных массивов
- 14. Обычно в программировании используются одномерные и двумерные
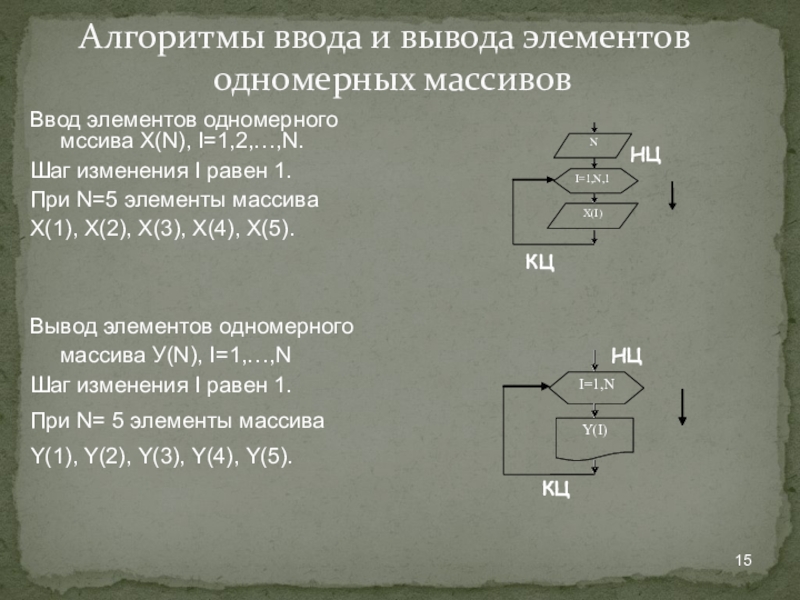
- 15. 15Алгоритмы ввода и вывода элементов одномерных массивовВвод
- 16. Алгоритм вычисления суммы элементов массива и среднего значенияВычислить
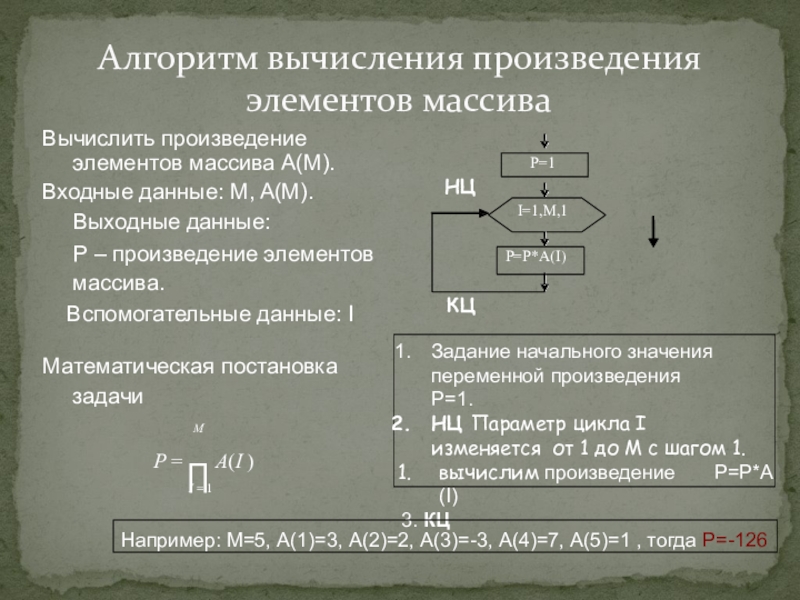
- 17. Алгоритм вычисления произведения элементов массиваВычислить произведениеэлементов массива
- 18. 18Алгоритм объединения двух массивов c суммированием их
- 19. Алгоритм подсчета количества элементов массива, удовлетворяющих заданному условиюПодсчитать количество
- 20. 0Алгоритм суммирования элементов массива, удовлетворяющих заданному условиюПросуммировать элементы
- 21. Алгоритм объединения двух массивов с чередованием элементовОбъединить
- 22. Алгоритм нахождения максимального элемента массиваНайти максимальный (минимальный)
- 23. Алгоритм формирования массива из элементов другого массива, удовлетворяющих условиюI=1,N J=J+1J= 0A(I)
- 24. Алгоритм удаления элемента из массиваУдаление К элемента
- 25. Лекция 6 Инфо25Алгоритм включения нового элемента в массив в
- 26. Алгоритм перестановки двух элементов массива местамиПерестановка К и
- 27. Алгоритм инвертирования (перестановки) элементов массива•Инвертирование массива А размерностью
- 28. Алгоритмы со структурой вложенных циклов••••В цикл, называемый
- 29. Алгоритм сортировки элементов массива•••••Упорядочить (отсортировать) элементы массива (В(1),
- 30. Алгоритм сортировки элементов массива (вложенные циклы)•Упорядочение (сортировка)
- 31. Типовые алгоритмы обработки двумерных массивов
- 32. Двумерные массивы•••••Двумерный массив – это таблица, содержащая
- 33. Ввод и вывод элементов двумерных массивовВвод элементов
- 34. Алгоритм вычисления среднего значения элементов массива по
- 35. Алгоритм вычисления среднего значения элементов массива по
- 36. Алгоритм транспонирования матрицыТранспонирование матрицы . Замена строк
- 37. Алгоритм произведения матрицы А(N,M) на вектор B(M)Входные
- 38. 38Алгоритм преобразования матрицы в одномерный массивПреобразовать массив А(N,М)
- 39. Алгоритм нахождения максимального элемента в строках двумерного
- 40. Алгоритм удаления строки из матрицыA(I , J
- 41. 41Алгоритм включения строки в матрицуВключить строку Х(M)
- 42. 42В Р записывается J-й элемент L строки,в
- 43. Алгоритм умножения двух матриц(количество столбцов первой матрицы
Слайд 2Содержание
Алгоритм с итерационным циклом.
Запоминание результатов.
Типовые алгоритмы обработки одномерных массивов.
Типовые алгоритмы обработки
Слайд 3Задача вычисления значений членов бесконечного ряда
с заданной точностью
,...
2! n!
õ, ,...,
x2 xn
Вычислить значения членов бесконечного
n!
с точностью до члена ряда
xn
Слайд 4Решение осуществляется в итерационном цикле, так как заранее не известно, при
Для итерационных циклов число повторений зависит не от параметров цикла, а от некоторого промежуточного или окончательного результата.
Сравнивая два соседних члена ряда, можно заметить, что уn / yn-1=x/n.
Слайд 5Для вычисления текущего члена ряда в цикле используется рекуррентная формула Уn
*x/n.
Для первого члена ряда У1 = У0 *x/1 задается У0
=1.
Параметр, изменяющийся в этом цикле – номер члена ряда n.
Формула для вычисления текущего члена ряда У=У* х/n.
2! 3! n!
õ, , ,...,
x2 x3 xn
n!
xn
Члены ряда У
n
Условие
завершения Ón
цикла
Слайд 6Блок-схема алгоритма вычисления членов ряда
Ввести значения Х и ε.
Задать n=1 и
НЦ
Вычислить следующий член ряда
Уn =Уn *Х/n
Напечатать n и Уn.
Вычислить номер следующего члена ряда n=n+1.
n
3.4. Если У >ε то перейти к НЦ.
3.5. КЦ
4. Конец
Уn= Уn Х/n
n=n+1
Начало
Х,
Да
Yn=1, n=1
Уn >
n, Уn
Конец
КЦ
НЦ
Слайд 7Запоминание результатов
В приведённых выше примерах результаты вычислений рассматривались как простые переменные. Поэтому
Новые значения сохраняясь в переменной затирали её старые значения.
Слайд 8Запоминание результатов
Если требуется сохранить в памяти (запомнить) все значения результатов, то необходимо:
Выделить
Вычислять результат как переменную с индексом.
Слайд 9Массив – это упорядоченная последовательность величин, обозначаемая одним именем.
Упорядоченность заключается в
При описании массива в программе указываются его имя и размер, то есть количество элементов в массиве.
Например, Х(N), массив с именем Х, содержит N элементов. Отдельные элементы этого массива запишутся так: Х(0), Х(1), Х(2),…, Х(N), то есть элементы имеют такое же имя как массив и отличаются друг от друга индексом.
Слайд 10Номер элемента называется Индексом. Индексы в массиве записываются в скобках.
Индексом может
Действия над элементами массивов обычно производятся в циклах, при этом параметром цикла являются переменные, обозначающие индексы элементов массивов.
Слайд 11Алгоритмы табулирования функций с запоминанием результатов.
У(I)= а-Х(I)2
Х(I)=Х(I-1)+h
Начало
Хн,Хк,h,a
Да
I= 1
I
Вычислим количество точек n=(Хк-Хн)/h+1 , для которых будут вычислены Х и У, n определяет размерность массивов.
Задаем начальное значение параметра цикла I=1 (I – это номер точки).
4. Задаем X(I)=x
н
5. НЦ1
Вычислим У(I)=a*X(I)2
Вычислим I=I+1
Вычислим X(I)=X(I-1)+h
5.4. Если I<=n идти к НЦ
КЦ1
НЦ2 Параметр цикла I изменяется от 1 до n с шагом 1.
7.1 Печать массивов Х(I), Y(I)
КЦ2
Конец.
НЦ1
НЦ2
КЦ1
КЦ2
Слайд 12сть 2
12
Алгоритмы табулирования функций с использованием блока модификации
Х(I)=Х(I-1)+h
Хн,Хк,h,a
n=(Хк-Хн)/h+1
Х(I), У(I)
I=1,n,1
Конец
I=1,n,1
У(I)= а-Х(I)2
Введем хн,
Вычислим количество точек n=(Хк-Хн)/h+1, для которых будут вычислены Х и У, n - определяет размерность массивов.
Задаем начальное значение X(1)=xn
Задаем начальное значение параметра цикла I=1 (I – это номер точки).
Задаем X(I)=xн
НЦ1 Параметр цикла I изменяется от 1 до n с шагом 1.
Вычислим У(I)=a*X(I)2
Вычислим X(I)=X(I-1)+h
КЦ1
НЦ2 Параметр цикла I изменяется от 1 до n с шагом 1.
8.1 Печать массивов Х(I), Y(I)
КЦ2
Конец.
НЦ1
НЦ2
КЦ2
КЦ1
Начало
X(1)= Хн
Слайд 14Обычно в программировании используются одномерные и двумерные массивы.
Одномерные массивы – это
В математике аналогом одномерного массива является вектор-строка или вектор –столбец.
Слайд 1515
Алгоритмы ввода и вывода элементов одномерных массивов
Ввод элементов одномерного
мссива X(N), I=1,2,…,N.
При N=5 элементы массива Х(1), Х(2), Х(3), X(4), X(5).
Вывод элементов одномерного массива У(N), I=1,…,N
Шаг изменения I равен 1. При N= 5 элементы массива Y(1), Y(2), Y(3), Y(4), Y(5).
Х(I)
N
Y(I)
КЦ
НЦ
I=1,N
КЦ
НЦ
I=1,N,1
Слайд 16Алгоритм вычисления суммы элементов массива и среднего значения
Вычислить среднее значение элементов массива
Входные данные: M, A(M).
Выходные данные: S – сумма элементов массива, SR – среднее значение.
Вспомогательные данные: I
Математическая постановка задачи
M
S
M
S A(I ) SR
I 1
I=1,M,1
S=S+A(I)
S=0
SR=S/M
Задание начального значения переменной суммы S=0.
НЦ Параметр цикла I изменяется
2.1.
от 1 до М с шагом 1.
Вычисление суммы S=S+А(I).
КЦ
Вычисление среднего SR=S/M.
Например: M=5, А(1)=3, А(2)=2, А(3)=-3, А(4)=7, А(5)=1 , тогда S=10, SR=2 16
НЦ
КЦ
Слайд 17Алгоритм вычисления произведения элементов массива
Вычислить произведение
элементов массива А(М).
Входные данные: M, A(M).
Выходные
Р – произведение элементов массива.
Вспомогательные данные: I
Математическая постановка задачи
M
P A(I )
I 1
I=1,M,1
P=P*A(I)
P=1
Задание начального значения переменной произведения Р=1.
НЦ Параметр цикла I изменяется от 1 до М с шагом 1.
вычислим произведение Р=Р*А(I)
3. КЦ
Например: M=5, А(1)=3, А(2)=2, А(3)=-3, А(4)=7, А(5)=1 , тогда P=-126
НЦ
КЦ
Слайд 1818
Алгоритм объединения двух массивов c суммированием их элементов
Объединить два массива А
С(I)=A(I) +B(I)
Входные данные: M, A(M), B(M).
Выходные данные: C(M) – массив результатов.
Вспомогательные данные: I текущее значение индекса элементов массива.
I=1,M,1
C(I)=A(I)+B(I)
Например: M=5, Массив А: 3, 2, -3, 7, 1
Массив B: 4, 3, 1,-5, 5
Тогда
Массив С: 7, 5,-2, 2,6
НЦ
КЦ
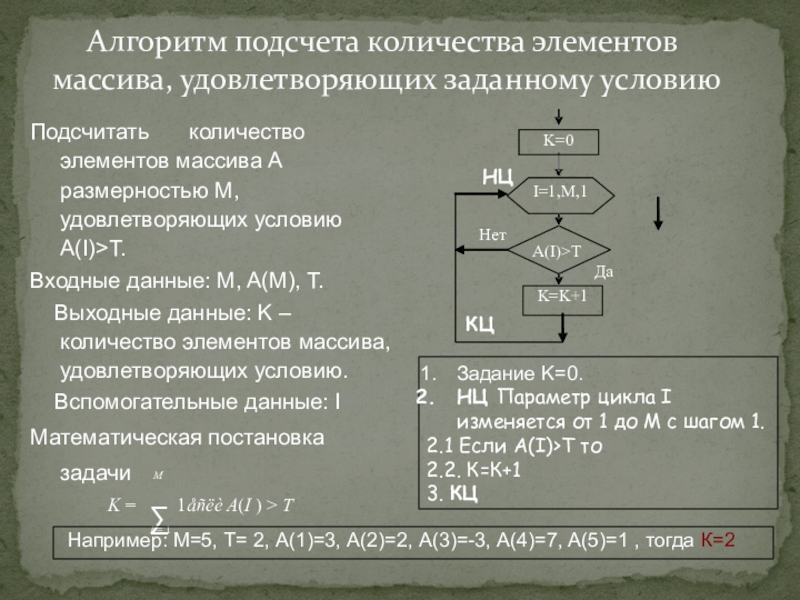
Слайд 19Алгоритм подсчета количества элементов массива, удовлетворяющих заданному условию
Подсчитать количество элементов массива А размерностью
Входные данные: M, A(M), T.
Выходные данные: K – количество элементов массива, удовлетворяющих условию.
Вспомогательные данные: I Математическая постановка
задачи
M
K 1 åñëè A(I ) T
I 1
I=1,M,1
K=K+1
K=0
A(I)>T
Да
Нет
Задание K=0.
НЦ Параметр цикла I изменяется от 1 до М с шагом 1.
2.1 Если А(I)>T то
2.2. К=К+1
3. КЦ
Например: M=5, Т= 2, А(1)=3, А(2)=2, А(3)=-3, А(4)=7, А(5)=1 , тогда К=2
НЦ
КЦ
Слайд 200
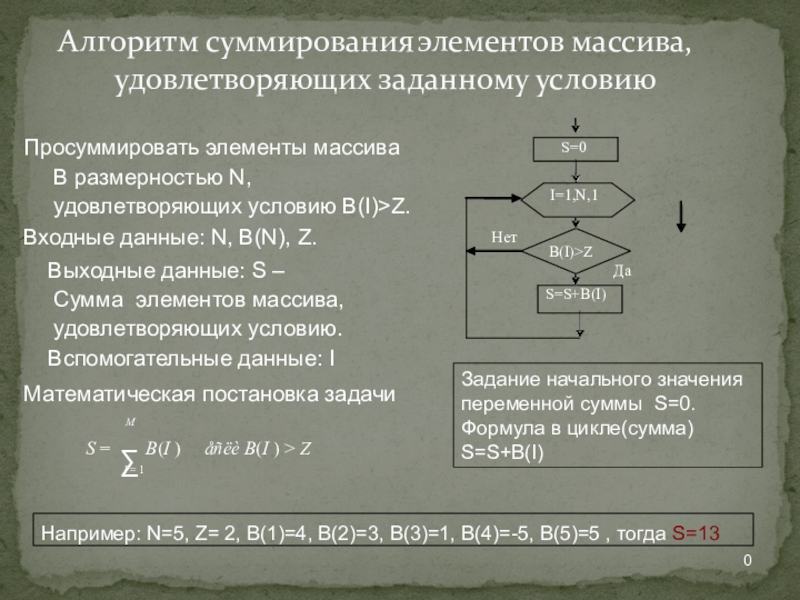
Алгоритм суммирования элементов массива, удовлетворяющих заданному условию
Просуммировать элементы массива В размерностью N,
Входные данные: N, B(N), Z.
Выходные данные: S – Сумма элементов массива, удовлетворяющих условию.
Вспомогательные данные: I Математическая постановка задачи
M
S B(I ) åñëè B(I ) Z
I 1
I=1,N,1
S=S+B(I)
S=0
B(I)>Z
Да
Нет
Задание начального значения переменной суммы S=0.
Формула в цикле(сумма) S=S+B(I)
Например: N=5, Z= 2, В(1)=4, В(2)=3, В(3)=1, В(4)=-5, В(5)=5 , тогда S=13
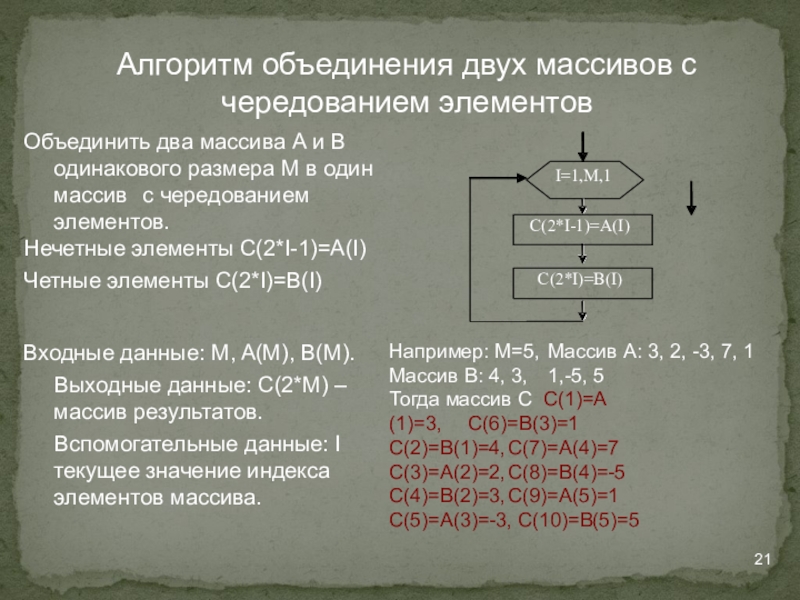
Слайд 21Алгоритм объединения двух массивов с чередованием элементов
Объединить два массива А и
Нечетные элементы С(2*I-1)=A(I) Четные элементы С(2*I)=B(I)
Входные данные: M, A(M), B(M).
Выходные данные: C(2*M) – массив результатов.
Вспомогательные данные: I текущее значение индекса элементов массива.
I=1,M,1
C(2*I-1)=A(I)
C(2*I)=B(I)
Например: M=5, Массив А: 3, 2, -3, 7, 1
Массив B: 4, 3, 1,-5, 5
Тогда массив С С(1)=А(1)=3, С(6)=В(3)=1
С(2)=В(1)=4, С(7)=А(4)=7
С(3)=А(2)=2, С(8)=В(4)=-5
С(4)=В(2)=3, С(9)=А(5)=1
С(5)=А(3)=-3, С(10)=В(5)=5
Слайд 22Алгоритм нахождения максимального элемента массива
Найти максимальный (минимальный) элемент массива В размерностью
Входные данные: N, B(N).
Выходные данные: BMAX – максимальный элемент массива, К
–номер индекса максимального элемента.
Вспомогательные данные: I
АНАЛОГИЧНО осуществляется поиск минимального элемента в массиве.
I=1,N
BMAX=B(I)
K= 1
BMAX>B(I
Да
Нет
BMA=B(1)
K= I
Задание начального значения переменной суммы BMAX=B(1), K=1.
Формула в цикле ВМАХ=B(I), K=I, если ВМАХ>B(I)
Например: N=5, B(1)=3, B(2)=2, B(3)=-3, B(4)=7, B(5)=1 , тогда BMAX=7, K=4
Слайд 23Алгоритм формирования массива из элементов другого массива, удовлетворяющих условию
I=1,N
J=J+1
J= 0
A(I)
Формулы в цикле: J=J+1 и В(J)=A(I), если А(I)
Сформировать новый массив В из элементов массива А размерностью N, удовлетворяющих условию A(I) åñëè A(I ) T J J 1, B(J ) A(I ) Например: N=5, Т= 2, Массив А:3, 2, -3, 7,1, тогда массив В(1)=-3, В(2)=1
Выходные данные: B(J), J – массив В и количество элементов массива.
Вспомогательные данные: I Математическая постановка задачи
N
I 1
Слайд 24Алгоритм удаления элемента из массива
Удаление К элемента из массива А размерностью
Удалить К элемент из массива можно сдвинув весь «Хвост» массива, начиная с К+1 элемента на одну позицию влево, выполняя операцию: А(I)=A(I+1), I=K, K+1,…,M
Входные данные: M, A(M), К.
Выходные данные: А(M-1) – массив результата (на один элемент меньше исходного).
Вспомогательные данные: I текущее значение индекса элементов массива.
A(I)=A(I+1)
Например: M=5, К=2 Массив А: 3, 6, -3, 7, 1
Тогда результат Массив А: 3, -3, 7, 1
Параметр цикла I изменяется от К до М-1.
Формула в цикле: A(I)=A(I +1).
I=K, M-1
Слайд 25Лекция 6 Инфо
25
Алгоритм включения нового элемента в массив в указанную позицию
Включение элемента D
Перед включением элемента нужно раздвинуть массив, начиная с К позиции, т.е. сдвинуть весь «хвост» массива, начиная с К+1 элемента на одну позицию вправо, выполняя операцию: А(I+1)=A(I), I=M, M -1,…,K,
( шаг изменения I= -1)
Перемещение элементов нужно начинать с конца.
Входные данные: M, A(M), К,D.
Выходные данные: А(M+1) – массив результата (на один элемент больше исходного).
Вспомогательные данные: I текущее значение индекса элементов массива.
A(I+1)=A(I)
A(K)=D
M=M+1
Например: M=5, К=2, D=8 Массив А: 3, 2, -3, 7, 1
Тогда результат
Параметр цикла I изменяется от М до К с шагом -1.
Формула в цикле: A(I+1)=A(I). Включение в К позицию массива значения переменной D
A(K)=D, увеличение размера массива М=М+1
I=M, K,-1
Слайд 26Алгоритм перестановки двух элементов массива местами
Перестановка К и L элементов массива А
Перезапись осуществляется с использованием вспомогательной переменной Р, в которую временно помещается один из элементов массива.
Например, в Р записывается К-й элемент массива, затем в К-й элемент записывается L-й, в L-й из переменной Р переписывается K-й.
Входные данные: M, A(M), K, L.
Выходные данные: А(M) –массив c переставленными элементами.
Вспомогательные данные: I , Р
P=A(K)
A(K)=A(L)
A(L)=P
Например: M=5, К=2, L=4 Массив А: 3, 2, -3, 7, 1
Тогда результат Массив А: 3, 7, -3, 2, 1
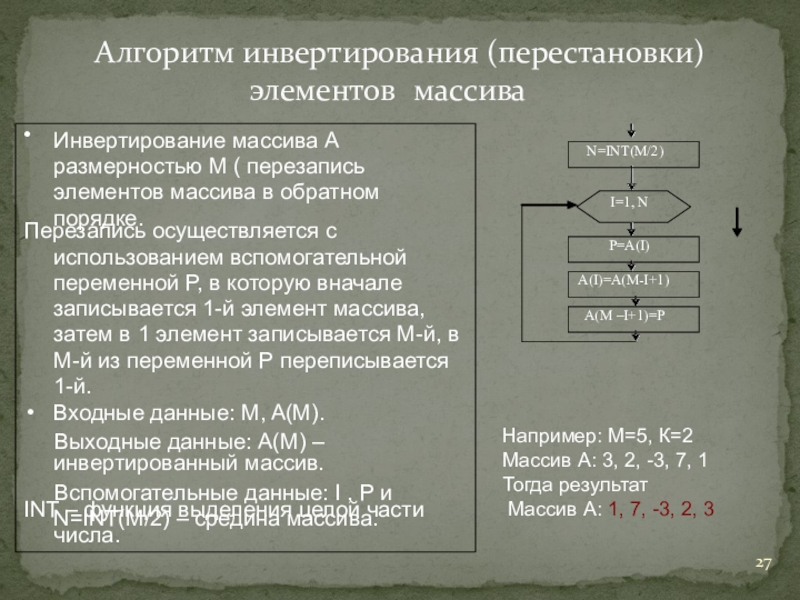
Слайд 27Алгоритм инвертирования (перестановки) элементов массива
•
Инвертирование массива А размерностью М ( перезапись элементов
Перезапись осуществляется с использованием вспомогательной переменной Р, в которую вначале записывается 1-й элемент массива, затем в 1 элемент записывается М-й, в M-й из переменной Р переписывается 1-й.
Входные данные: M, A(M).
Выходные данные: А(M) – инвертированный массив.
Вспомогательные данные: I , Р и N=INT(M/2) – средина массива.
INT – функция выделения целой части числа.
I=1, N
P=A(I)
N=INT(M/2)
A(I)=A(M-I+1)
A(M –I+1)=P
Например: M=5, К=2 Массив А: 3, 2, -3, 7, 1
Тогда результат Массив А: 1, 7, -3, 2, 3
Слайд 28Алгоритмы со структурой вложенных циклов
•
•
•
•
В цикл, называемый внешним, могут входить один
Организация внешнего и внутренних циклов осуществляется по тем же правилам, что и простого цикла.
Параметры внешнего и внутреннего циклов разные и изменяются не одновременно, то есть при одном значении параметра внешнего цикла параметр внутреннего цикла принимает поочередно все значения.
Приемы программирования, изложенные ранее, можно использовать и при организации вложенных циклов.
Слайд 29Алгоритм сортировки элементов массива
•
•
•
•
•
Упорядочить (отсортировать) элементы массива (В(1), В(2), В(3), В(4), …,
Для решения используется алгоритм, состоящий из двух циклов:
Внешний цикл – это номер просмотра массива или его части и перестановки найденного во внутреннем цикле минимального элемента массива с первым .
Во внутреннем цикле первый элемент массива или его части сравнивается со всеми последующими элементами. И находится минимальный элемент.
Для упорядочения всех элементов массива внешний цикл повторяется К=1,…, N-1 раз. Количество повторений внутреннего цикла на каждом шаге внешнего цикла равно N – К раз. Когда остается в массиве последний элемент сортировка завершена.
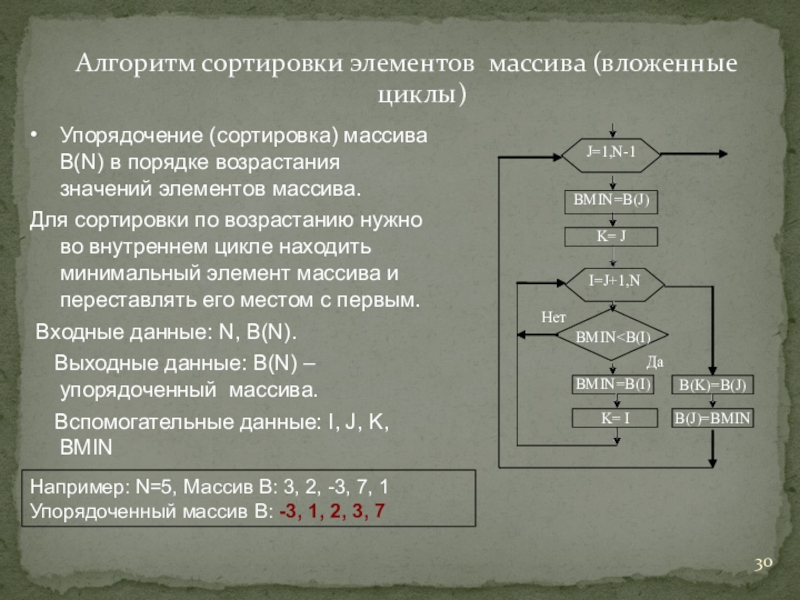
Слайд 30Алгоритм сортировки элементов массива (вложенные циклы)
•
Упорядочение (сортировка) массива В(N) в порядке
Для сортировки по возрастанию нужно во внутреннем цикле находить минимальный элемент массива и переставлять его местом с первым.
Входные данные: N, B(N).
Выходные данные: В(N) – упорядоченный массива.
Вспомогательные данные: I, J, K, BMIN
I=J+1,N
BMIN=B(I)
K= J
Да
Нет BMIN=B(J) K= I J=1,N-1 B(J)=BMIN B(K)=B(J) Например: N=5, Массив B: 3, 2, -3, 7, 1
BMIN
Упорядоченный массив В: -3, 1, 2, 3, 7
Слайд 32Двумерные массивы
•
•
•
•
•
Двумерный массив – это таблица, содержащая информацию и состоящая из
Каждый элемент двумерного массива имеет тоже имя, что и весь массив и отличается от другого элемента номером строки и номером столбца, на пересечении которых он находится.
Номер строки и номер столбца называются индексами.
Индексы в двумерном массиве записываются в скобках через запятую. На первом месте стоит индекс строки, на втором месте – индекс столбца.
Например, В(I,J) –элемент двумерного массива с именем В, стоящий на пересечении I строки и J столбца.
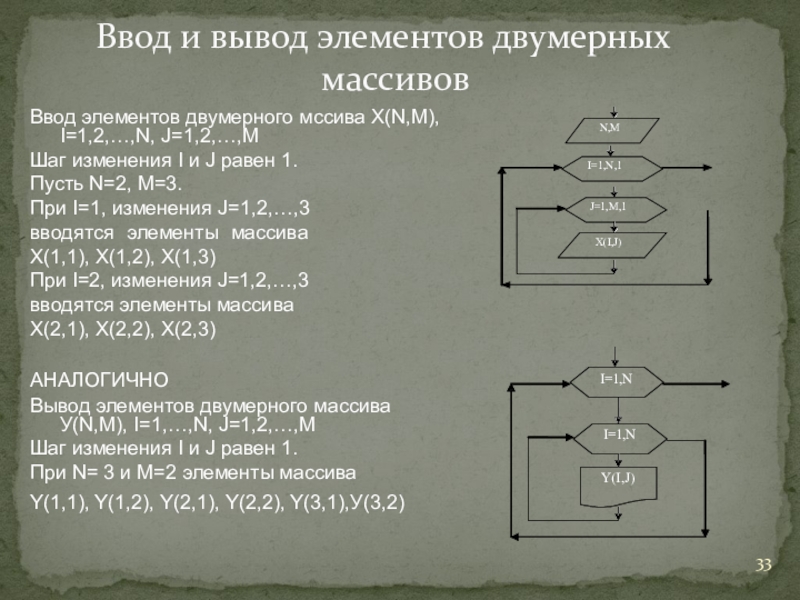
Слайд 33Ввод и вывод элементов двумерных массивов
Ввод элементов двумерного мссива X(N,M),
I=1,2,…,N, J=1,2,…,M
Шаг
При I=1, изменения J=1,2,…,3 вводятся элементы массива Х(1,1), Х(1,2), Х(1,3)
При I=2, изменения J=1,2,…,3 вводятся элементы массива X(2,1), X(2,2), X(2,3)
АНАЛОГИЧНО
Вывод элементов двумерного массива У(N,M), I=1,…,N, J=1,2,…,M
Шаг изменения I и J равен 1.
При N= 3 и M=2 элементы массива Y(1,1), Y(1,2), Y(2,1), Y(2,2), Y(3,1),У(3,2)
J=1,M,1
Х(I,J)
N,M
I=1,N,1
Y(I,J)
I=1,N
I=1,N
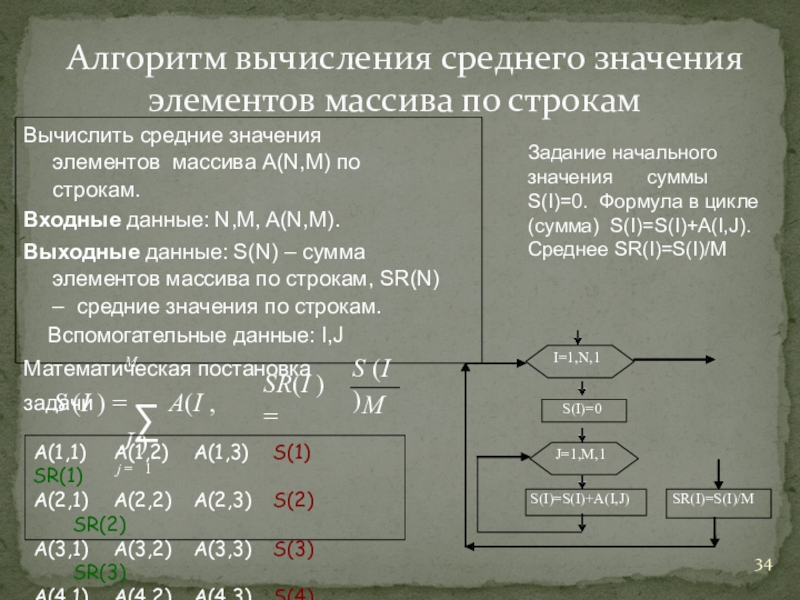
Слайд 34Алгоритм вычисления среднего значения элементов массива по строкам
Вычислить средние значения элементов
Входные данные: N,M, A(N,M).
Выходные данные: S(N) – сумма элементов массива по строкам, SR(N) – средние значения по строкам.
Вспомогательные данные: I,J Математическая постановка задачи
M
M
S (I )
SR(I )
S (I ) A(I , J )
j 1
J=1,M,1
S(I)=S(I)+A(I,J)
S(I)=0
SR(I)=S(I)/M
I=1,N,1
Задание начального значения суммы S(I)=0. Формула в цикле(сумма) S(I)=S(I)+А(I,J).
Среднее SR(I)=S(I)/M
А(1,1) А(1,2) А(1,3) S(1) SR(1)
А(2,1) А(2,2) A(2,3) S(2) SR(2)
А(3,1) А(3,2) А(3,3) S(3) SR(3)
А(4,1) А(4,2) A(4,3) S(4) SR(4)
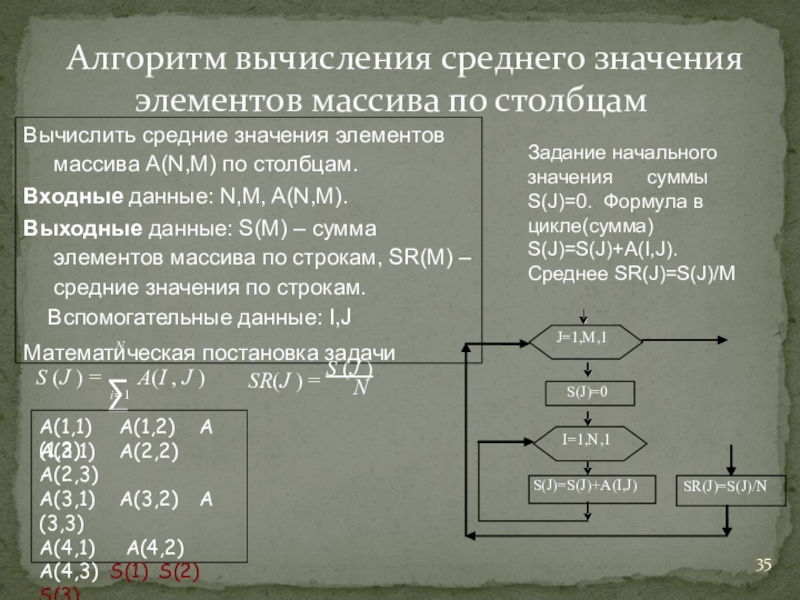
Слайд 35Алгоритм вычисления среднего значения элементов массива по столбцам
Вычислить средние значения элементов
Входные данные: N,M, A(N,M).
Выходные данные: S(M) – сумма элементов массива по строкам, SR(M) – средние значения по строкам.
Вспомогательные данные: I,J Математическая постановка задачи
N
SR(J ) S (J )
N
S (J ) A(I , J )
I=1,N,1
S(J)=S(J)+A(I,J)
S(J)=0
SR(J)=S(J)/N
J=1,M,1
Задание начального значения суммы S(J)=0. Формула в цикле(сумма) S(J)=S(J)+А(I,J).
Среднее SR(J)=S(J)/M
i 1
А(1,1) А(1,2) А(1,3)
А(2,1) А(2,2) A(2,3)
А(3,1) А(3,2) А(3,3)
А(4,1) А(4,2) A(4,3) S(1) S(2) S(3)
SR(1) SR(2) SR(3)
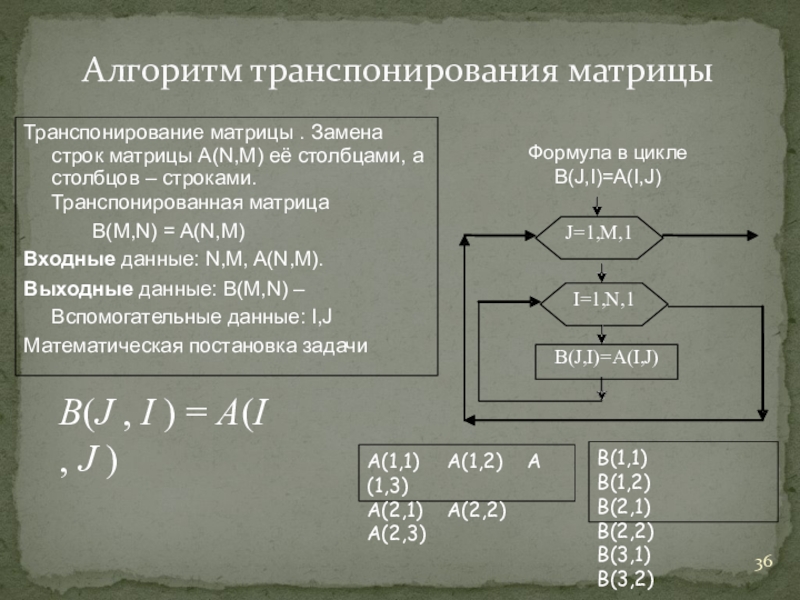
Слайд 36Алгоритм транспонирования матрицы
Транспонирование матрицы . Замена строк матрицы А(N,М) её столбцами,
Транспонированная матрица
В(M,N) = A(N,M)
Входные данные: N,M, A(N,M).
Выходные данные: B(M,N) – Вспомогательные данные: I,J
Математическая постановка задачи
B(J , I ) A(I , J )
I=1,N,1
B(J,I)=A(I,J)
J=1,M,1
Формула в цикле B(J,I)=А(I,J)
А(1,1) А(1,2) А(1,3)
А(2,1) А(2,2) A(2,3)
B(1,1) B(1,2)
B(2,1) B(2,2)
B(3,1) B(3,2)
Слайд 37Алгоритм произведения матрицы А(N,M) на вектор B(M)
Входные данные: N,M, A(N,M), B(M)
Выходные
Вспомогательные данные: I,J Математическая постановка
задачи
M
j 1
C(I ) A(I , J ) * B(J )
J=1,M,1
C(I)=C(I)+A(I,J)*B(J)
C(I)=0
I=1,N,1
Задание начального значения переменной C(I)=0.
Формула во внутреннем цикле С(I)=C(I)+А(I,J)*B(J).
С(1)
C(2)
C(3)
А(1,1) А(1,2) А(1,3)
А(2,1) А(2,2) A(2,3)
А(3,1) А(3,2) А(3,3)
B(1) B(2) B(3)
Слайд 3838
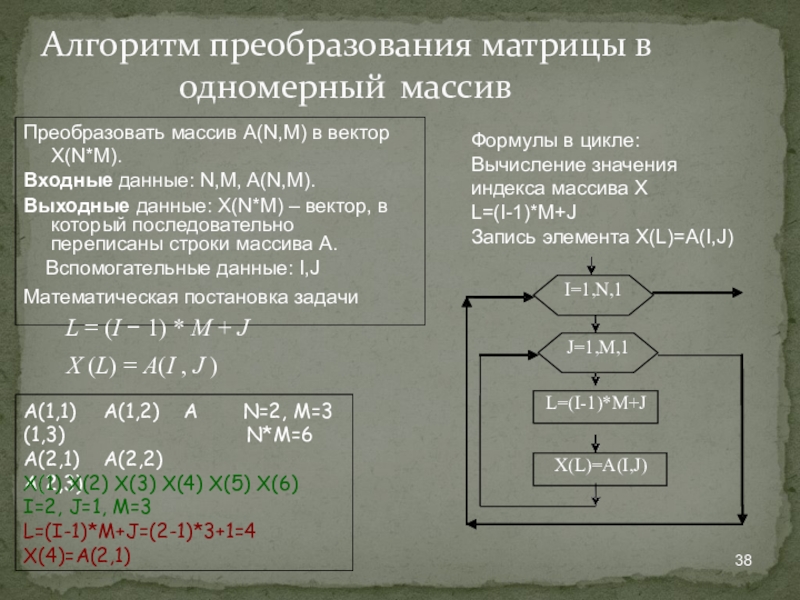
Алгоритм преобразования матрицы в одномерный массив
Преобразовать массив А(N,М) в вектор Х(N*M).
Входные данные:
Выходные данные: X(N*M) – вектор, в который последовательно переписаны строки массива А.
Вспомогательные данные: I,J Математическая постановка задачи
L (I 1) * M J X (L) A(I , J )
J=1,M,1
X(L)=A(I,J)
I=1,N,1
L=(I-1)*M+J
Формулы в цикле: Вычисление значения индекса массива Х L=(I-1)*M+J
Запись элемента X(L)=A(I,J)
А(1,1) А(1,2) А(1,3)
А(2,1) А(2,2) A(2,3)
N=2, M=3 N*M=6
X(1) X(2) X(3) X(4) X(5) X(6) I=2, J=1, M=3
L=(I-1)*M+J=(2-1)*3+1=4 X(4)=A(2,1)
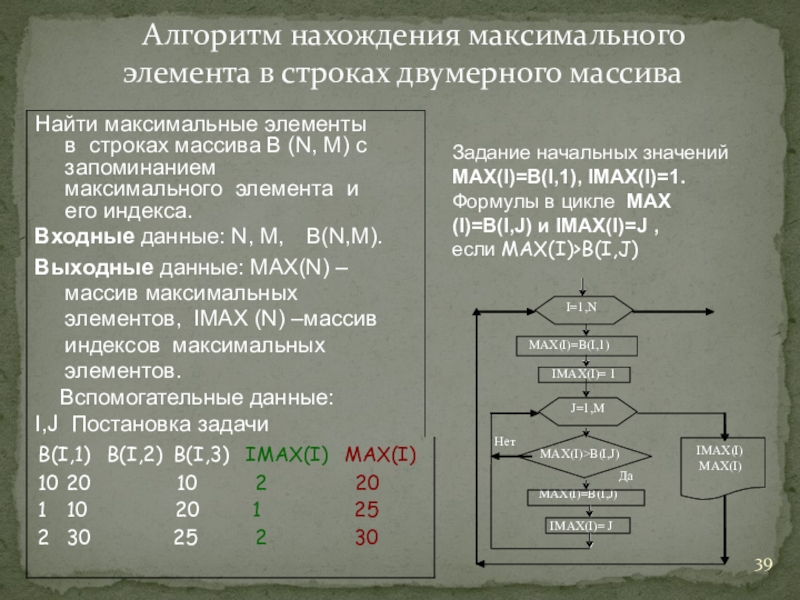
Слайд 39Алгоритм нахождения максимального элемента в строках двумерного массива
I=1,N
MAX(I)>B(I,J)
Да MAX(I)=B(I,J)
Нет
MAX(I)=B(I,1)
IMAX(I)= J
IMAX(I)= 1
J=1,M
IMAX(I)
Задание начальных значений
MAX(I)=B(I,1), IMAX(I)=1.
Формулы в цикле МАХ(I)=B(I,J) и IMAX(I)=J , если МАХ(I)>B(I,J)
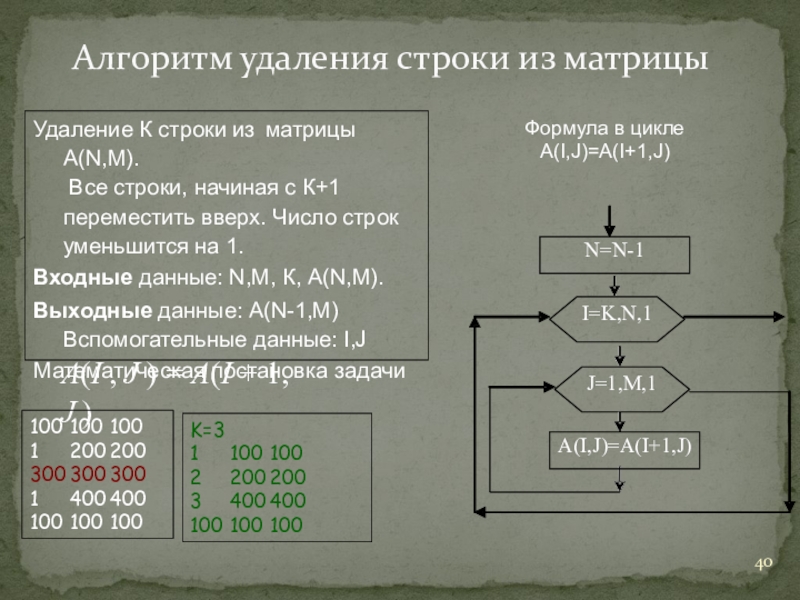
Слайд 40Алгоритм удаления строки из матрицы
A(I , J ) A(I
Удаление К строки из матрицы А(N,М).
Все строки, начиная с К+1 переместить вверх. Число строк уменьшится на 1.
Входные данные: N,M, К, A(N,M).
Выходные данные: А(N-1,M) Вспомогательные данные: I,J
Математическая постановка задачи
J=1,M,1
A(I,J)=A(I+1,J)
I=K,N,1
N=N-1
Формула в цикле A(I,J)=А(I+1,J)
100 100 100
1 200 200
300 300 300
1 400 400
100 100 100
K=3
1 100 100
2 200 200
3 400 400
100 100 100
Слайд 4141
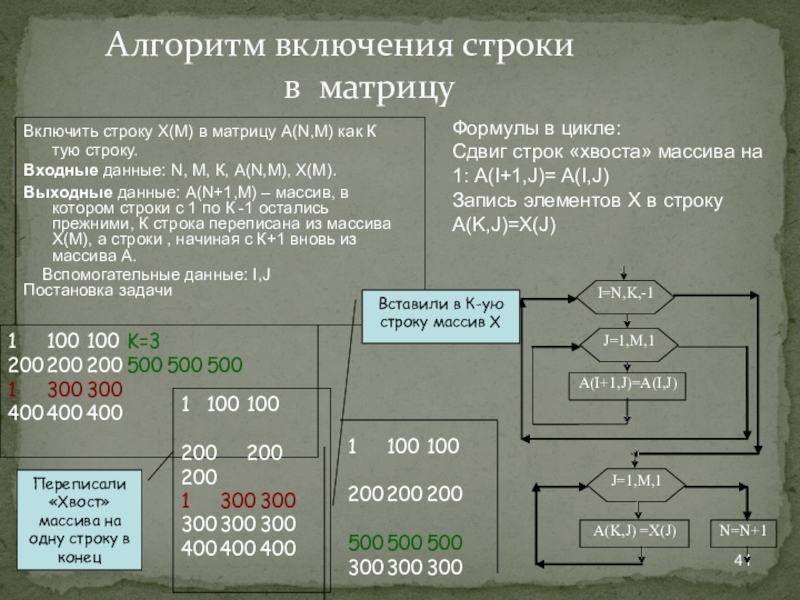
Алгоритм включения строки в матрицу
Включить строку Х(M) в матрицу А(N,М) как
Входные данные: N, M, К, A(N,M), X(M).
Выходные данные: A(N+1,M) – массив, в котором строки с 1 по К -1 остались прежними, К строка переписана из массива Х(М), а строки , начиная с К+1 вновь из массива А.
Вспомогательные данные: I,J
Постановка задачи
J=1,M,1
I=N,K,-1
A(I+1,J)=A(I,J)
J=1,M,1
A(K,J) =X(J)
N=N+1
Формулы в цикле:
Сдвиг строк «хвоста» массива на 1: А(I+1,J)= A(I,J)
Запись элементов X в строку A(K,J)=X(J)
1 300 300
400 400 400
1 100 100 K=3
200 200 200 500 500 500
1 100 100
200 200 200
1 300 300
300 300 300
400 400 400
1 100 100
200 200 200
500 500 500
300 300 300
Переписали
«Хвост» массива на одну строку в конец
Вставили в К-ую строку массив X
Слайд 4242
В Р записывается J-й элемент L строки,
в J элемент L строки
в J-й элемент K строки записывается элемент из переменной Р .
Алгоритм перестановки строк в матрице
Перестановка L и K строк в матрице А(N,M) осуществляется с использованием вспомогательной переменной Р:
Входные данные: N, M, A(N,M).
Выходные данные: А(N,M) – c переставленными строками.
Вспомогательные данные: I , J, Р, К.
J=1, M
P=A(L,J)
A(L,J)=A(K,J)
A(K,J)=P
L=2, K=4
4 40 40 40
50 50 50 50
L=2,K=4
1 10 10 10
2 20 20 20
3 30 30 30
P
1 10 10 10
40 40 40 40
1 30 30 30
20 20 20 20
50 50 50 50
РЕЗУЛЬТАТ
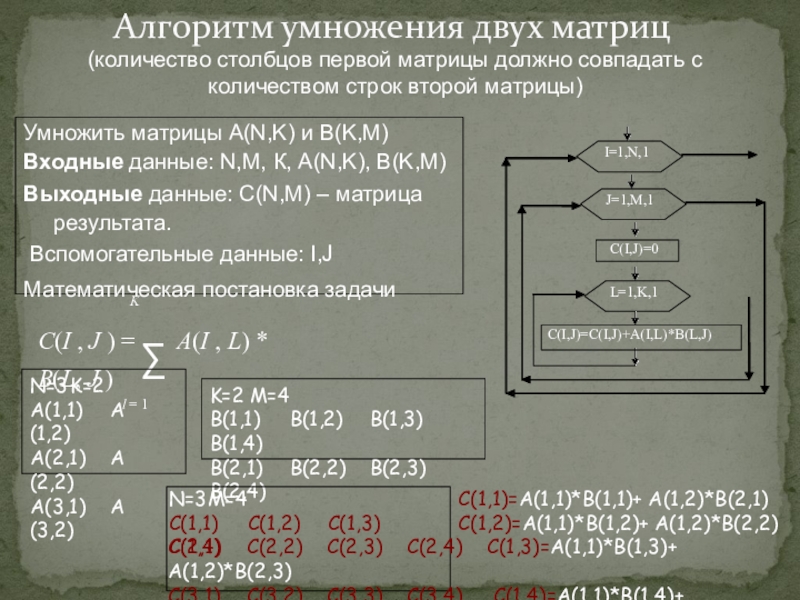
Слайд 43Алгоритм умножения двух матриц
(количество столбцов первой матрицы должно совпадать с количеством
Умножить матрицы А(N,K) и B(K,M)
Входные данные: N,M, К, A(N,K), B(K,M)
Выходные данные: C(N,M) – матрица результата.
Вспомогательные данные: I,J Математическая постановка задачи
K
C(I , J ) A(I , L) * B(L, J )
l 1
L=1,K,1
C(I,J)=C(I,J)+A(I,L)*B(L,J)
C(I,J)=0
J=1,M,1
I=1,N,1
N=3 K=2
А(1,1) А(1,2)
А(2,1) А(2,2)
А(3,1) А(3,2)
K=2 M=4
B(1,1) B(1,2) B(1,3) B(1,4)
B(2,1) B(2,2) B(2,3) B(2,4)
N=3 M=4
C(1,1) C(1,2) C(1,3) C(1,4)
C(1,1)=A(1,1)*B(1,1)+ A(1,2)*B(2,1)
C(1,2)=A(1,1)*B(1,2)+ A(1,2)*B(2,2)
C(2,1) C(2,2) C(2,3) C(2,4) C(1,3)=A(1,1)*B(1,3)+ A(1,2)*B(2,3)
C(3,1) C(3,2) C(3,3) C(3,4) C(1,4)=A(1,1)*B(1,4)+ A(1,2)*B(2,4)