- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок, Презентация Касательная к окружности
Содержание
- 1. Урок, Презентация Касательная к окружности
- 2. ПовторениеРасстояние между двумя точками-длина отрезка, соединяющего эти
- 3. ОкружностьАВСDОК
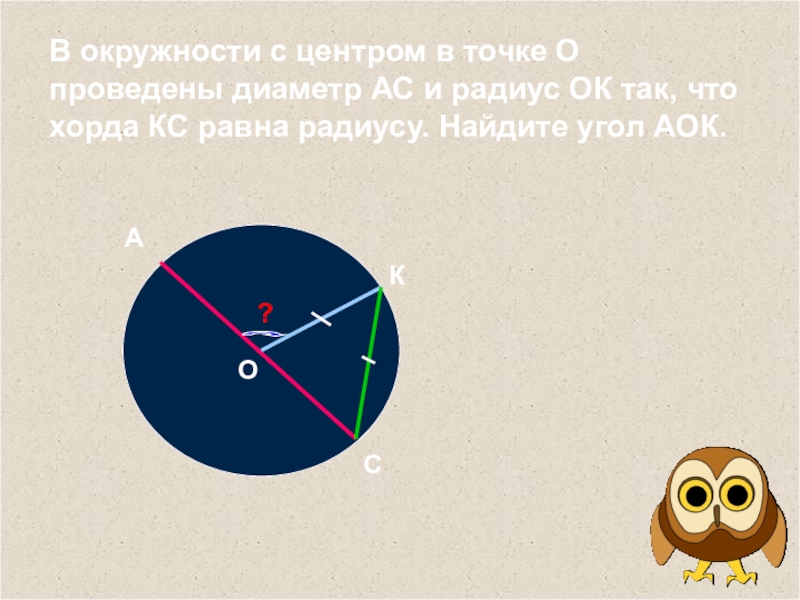
- 4. В окружности с центром в точке О
- 5. В окружности с центром в точке О
- 6. Взаимное расположение прямой и окружностиВозможны три случаяИмеют
- 7. Прямая и окружность имеют две общие точкиАВОН
- 8. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ Определение. Прямая,
- 9. (О свойстве касательной)Касательная к окружности перпендикулярна
- 10. Решите задачу.ВМО5смДано: Окр(О; r),
- 11. Каким может быть взаимное расположение прямой и
- 12. АСВ.
- 13. Теорема об отрезках касательных, проведённых из одной
- 14. № 631, 633 (устно)№ 634, 635, 638-644, 647 (письменно)Д/з п68,69 №632, 636Решим задачи из учебника:
Слайд 2Повторение
Расстояние между двумя точками-
длина отрезка, соединяющего эти точки
Расстояние от данной точки
длина перпендикуляра, проведённого из точки к прямой
Слайд 4
В окружности с центром в точке О проведены диаметр АС и
А
С
О
К
?
Слайд 5
В окружности с центром в точке О проведена хорда ВС, равная
В
С
О
r
r
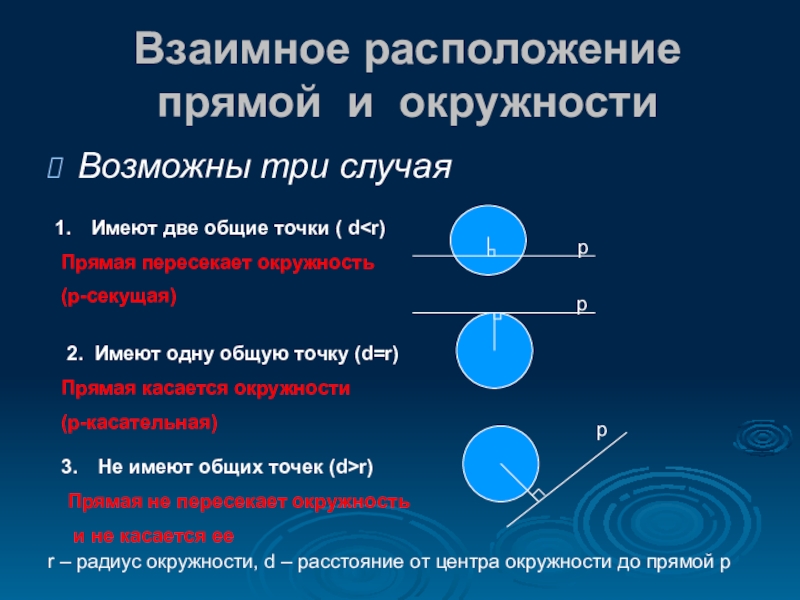
Слайд 6Взаимное расположение
прямой и окружности
Возможны три случая
Имеют две общие точки ( d
(р-секущая)
2. Имеют одну общую точку (d=r)
Прямая касается окружности
(р-касательная)
Не имеют общих точек (d>r)
Прямая не пересекает окружность
и не касается ее
r – радиус окружности, d – расстояние от центра окружности до прямой р
р
р
р
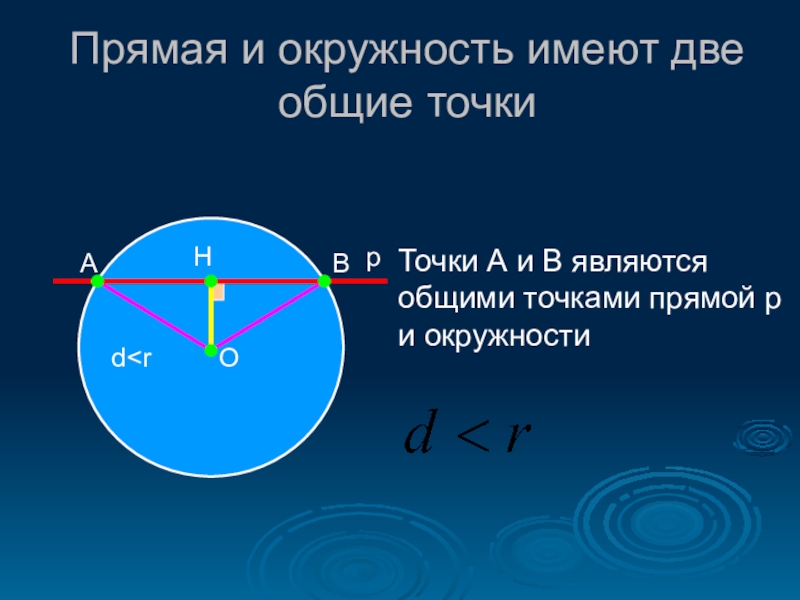
Слайд 7Прямая и окружность имеют две общие точки
А
В
О
Н
p
Точки А и В
d
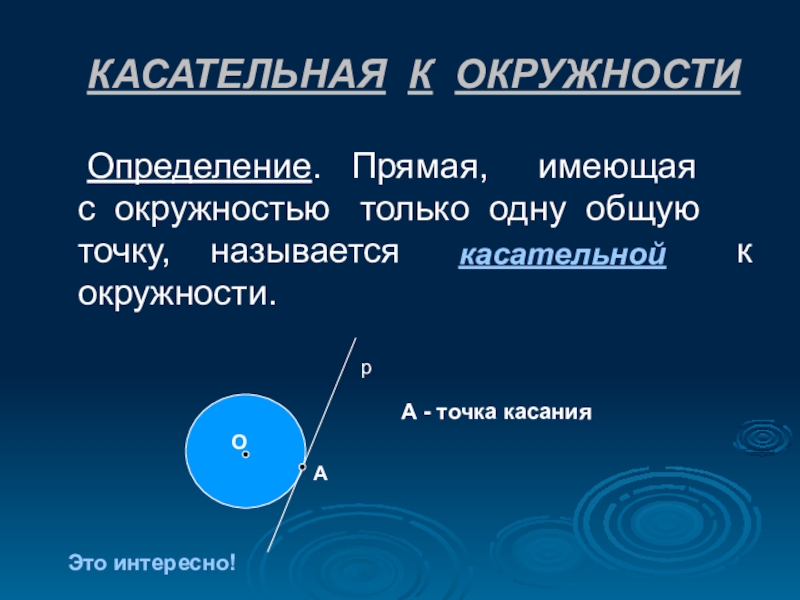
Слайд 8КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Определение. Прямая, имеющая
А
А - точка касания
О
р
Это интересно!
касательной
Слайд 9
(О свойстве касательной)
Касательная к окружности перпендикулярна к радиусу, проведенному
.
1.Пусть р ОА, тогда ОА – наклонная к прямой р.
2. Так как перпендикуляр , проведенный из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса.
3. Из пп. 1 и 2 следует прямая и окружность имеют две общие точки, что противоречит условию ( прямая р – касательная ).
Поэтому р ОА. Теорема доказана.
ТЕОРЕМА
Дано: окр(О,ОА), р – касательная к окружности, А – точка касания.
Доказать: р ОА
Доказательство:
Слайд 10
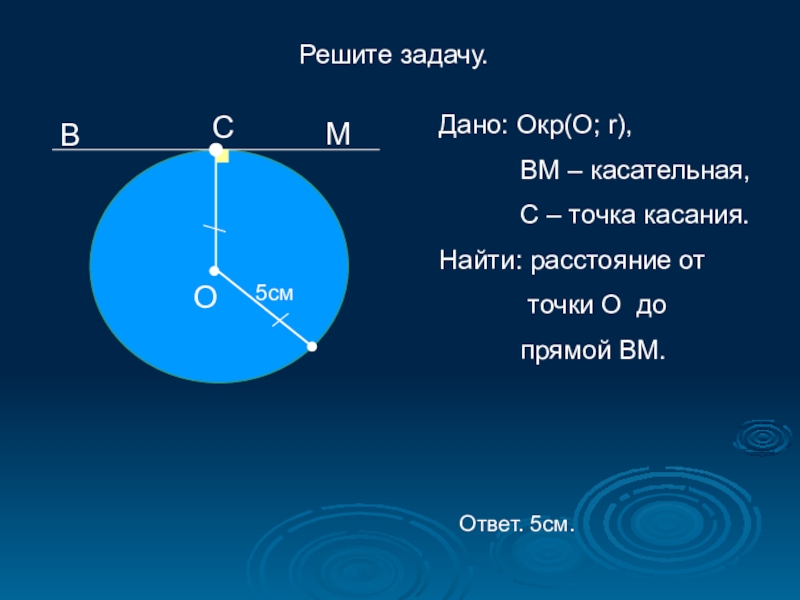
Решите задачу.
В
М
О
5см
Дано: Окр(О; r),
ВМ –
С – точка касания.
Найти: расстояние от
точки О до
прямой ВМ.
Ответ. 5см.
С
Слайд 11Каким может быть взаимное расположение прямой и окружности?
Как называется прямая, которая
Какая прямая называется касательной к окружности?
Какая точка называется точкой касания прямой и окружности?
Сформулируйте теорему о свойстве касательной ( к следующему уроку попробуй выучить доказательство).
Предлагаем ответить на вопросы теста по изученной теме
1) На рисунке прямая по отношению к окружности
А А секущая Б А секущая Б касательная С нет правильного ответа
2) Прямая – касательная по отношению к окружности.
Она образует с радиусом, проведенным в точку касания угол
А А острый Б А острый Б прямой С тупой
Проверь себя!
Слайд 13
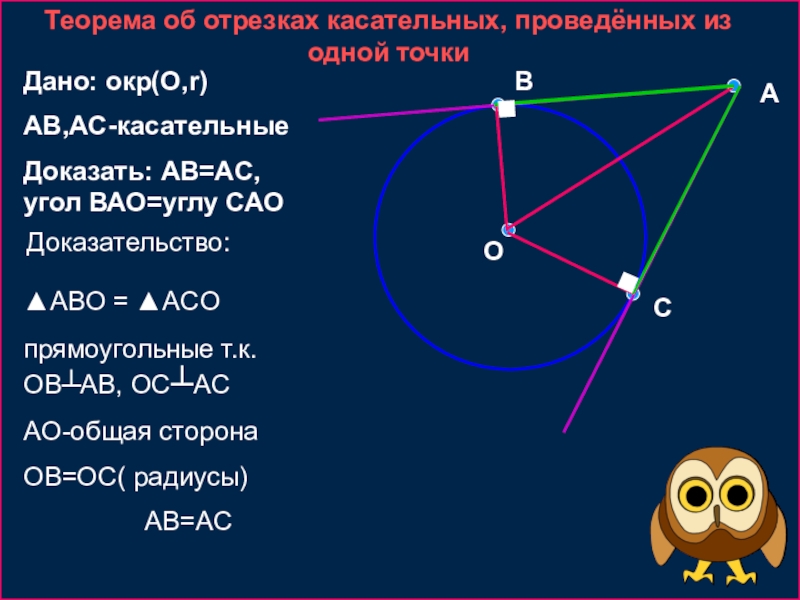
Теорема об отрезках касательных, проведённых из одной точки
А
С
О
B
Дано: окр(О,r)
AB,AC-касательные
Доказать: AB=AC, угол
▲ABO = ▲ACO
прямоугольные т.к. OB┴AB, OC┴AC
AO-общая сторона
OB=OC( радиусы)
AB=AC
Доказательство:
■
■
Слайд 14№ 631, 633 (устно)
№ 634, 635, 638-644, 647 (письменно)
Д/з п68,69 №632,
Решим задачи из учебника: