- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Пример кейса по математике:Задача о трапеции
Содержание
- 1. Пример кейса по математике:Задача о трапеции
- 2. Задача:На пол была пролита краска. Определить площадь поверхности пятна.
- 3. Вопросы для самостоятельного изучения и обсуждения В ходе
- 4. Для того чтобы решить поставленную задачу, необходимо
- 5. Какие задачи решают с помощью интеграла?Кто ввел
- 6. Оно представляет собой криволинейную трапецию, площадь которой
- 7. Криволинейной трапецией называется фигура, которая ограничена графиком
- 8. Чтобы перейти к решению нашей задачи необходимо
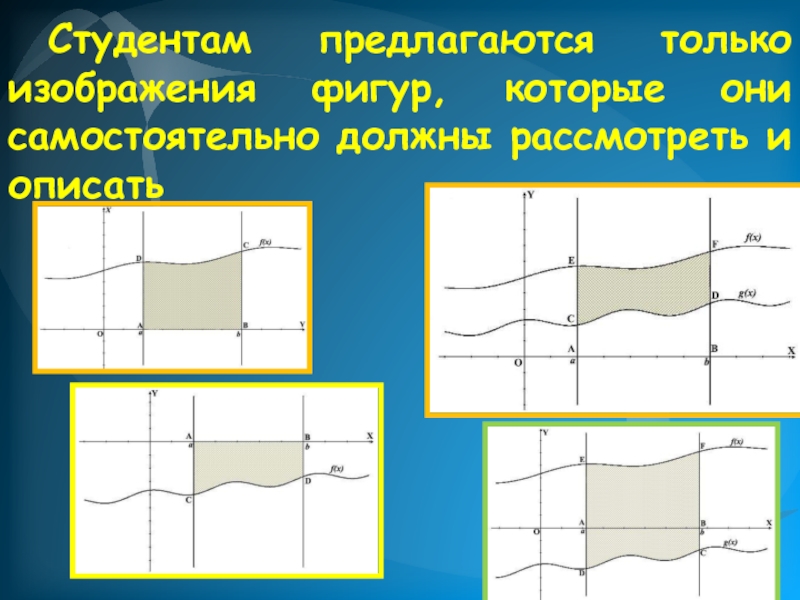
- 9. Студентам предлагаются только изображения фигур, которые они самостоятельно должны рассмотреть и описать
- 10. Ответы для обсуждения и проверки работы студентов
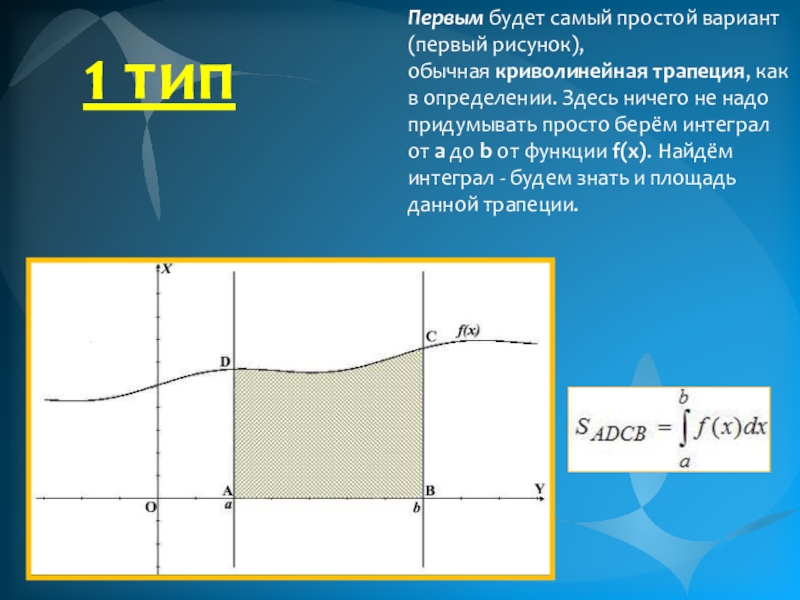
- 11. Первым будет самый простой вариант (первый рисунок), обычная криволинейная
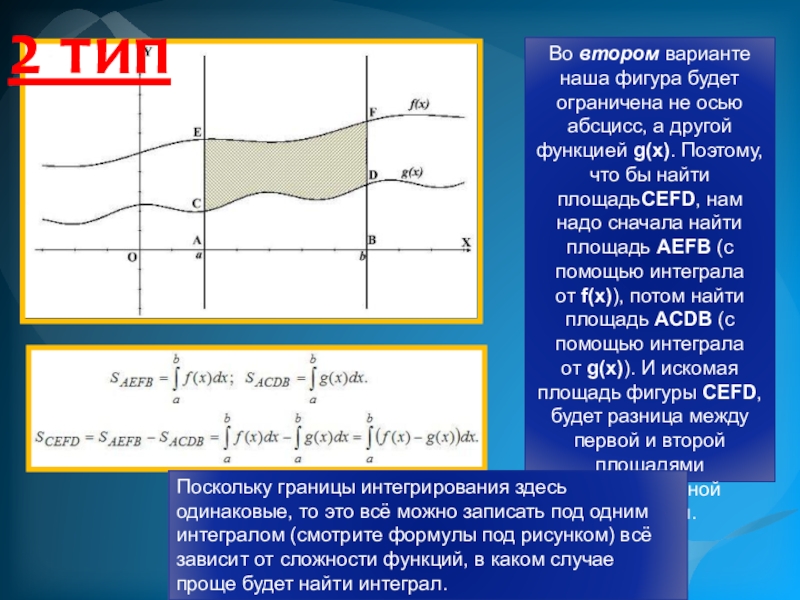
- 12. Во втором варианте наша фигура будет ограничена не осью
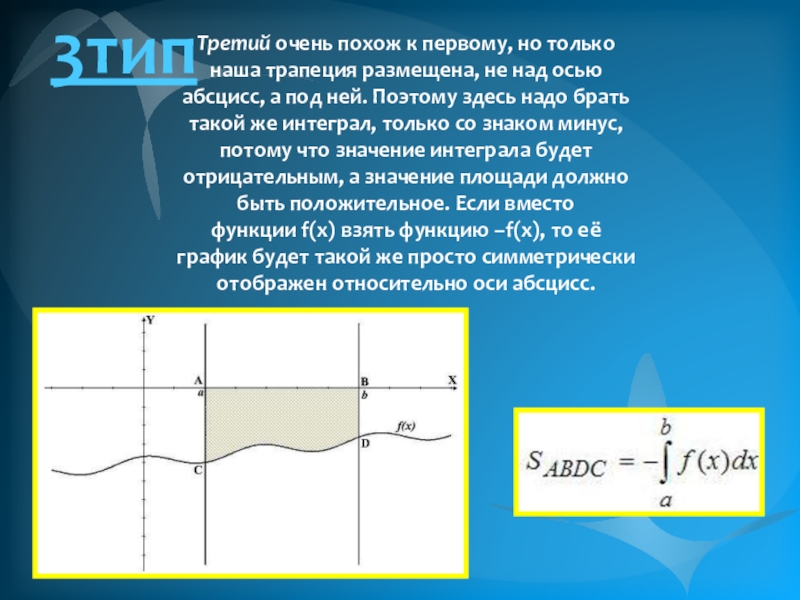
- 13. Третий очень похож к первому, но только наша
- 14. И четвёртый вариант, когда часть нашей фигуры находится над
- 15. Мы рассмотрели наиболее простые варианты, но теперь вернемся
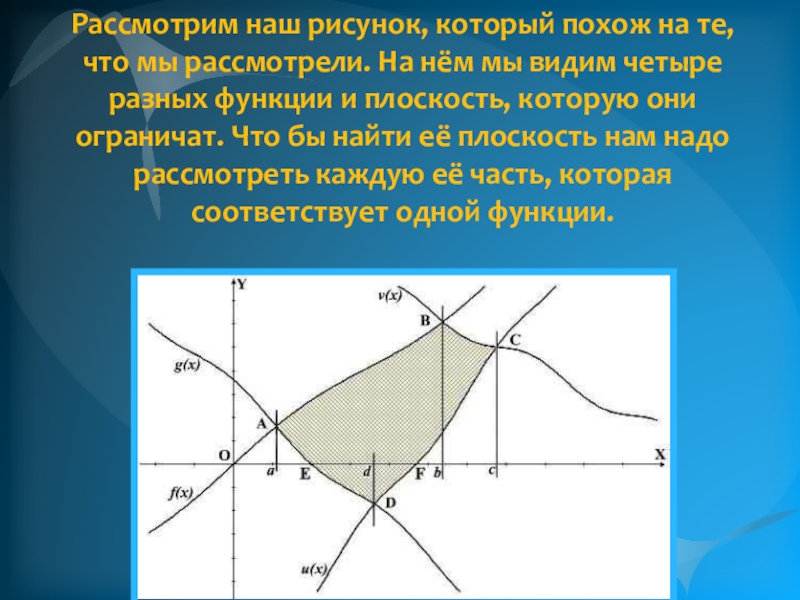
- 16. Рассмотрим наш рисунок, который похож на те,
- 17. Начнём с функции f(x) здесь нам надо искать интеграл
- 18. Наш ответ:
- 19. Вспомогательные вопросы для преподавателя к обсуждению и
- 20. Попробуйте понять, для чего лично Вам может
- 21. Творческо-самостоятельное задание на обобщение знаний. Особая задача
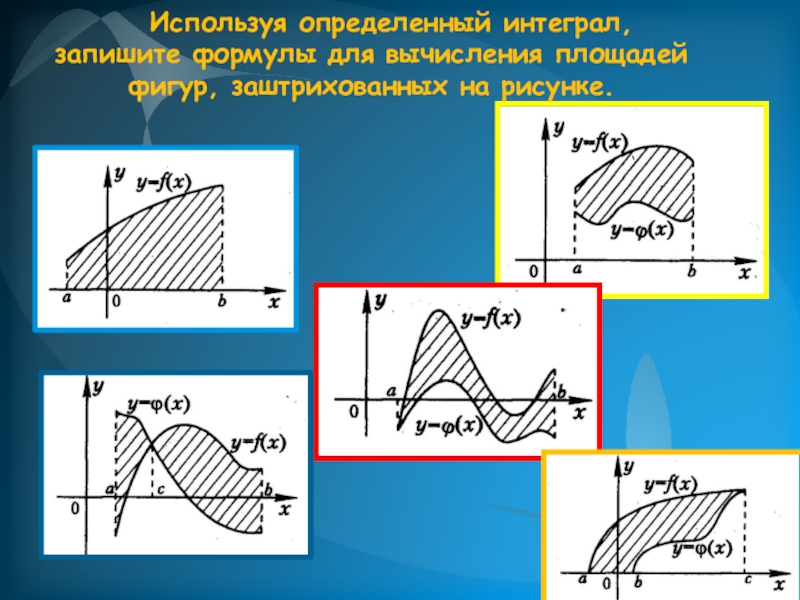
- 22. Используя определенный интеграл, запишите формулы для вычисления площадей фигур, заштрихованных на рисунке.
Слайд 3Вопросы для самостоятельного изучения и обсуждения
В ходе занятия формируется несколько групп
Слайд 4Для того чтобы решить поставленную задачу, необходимо выяснить, что из себя
Каким образом можно вычислить его площадь?
Почему именно применяя понятия определенного интеграла?
Слайд 5Какие задачи решают с помощью интеграла?
Кто ввел знаки производной и интеграла?
Что
Изобразить фигуру, для вычисления площади которой надо сложить значения соответствующего интеграла.
Рассказать о способе отыскания площади фигуры, составленной из двух не перекрывающих друг друга криволинейных трапеций.
Как вычислить площадь фигуры, если она ограничена графиком функции р(х), где р(х)<0?
Какое свойство площадей надо использовать при вычислении площадей фигур, имеющих сложную конфигурацию
Как называют формулу для нахождения площади криволинейной трапеции?
Вывести формулу для вычисления площади фигуры, составленной из неперекрывающихся криволинейных трапеций.
Вывести формулу для вычисления площади фигуры, полученной как разность криволинейных трапеций, которые образованы графиками функций, принимающих только положительные значения.
Вывести формулу для вычисления площади криволинейной трапеции, расположенной на отрицательной полуплоскости.
Слайд 6 Оно представляет собой криволинейную трапецию, площадь которой вам и придется искать.
В
Слайд 7Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной, неотрицательной функции f(x)
Слайд 8Чтобы перейти к решению нашей задачи необходимо рассмотреть возможные варианты расположения
Слайд 9 Студентам предлагаются только изображения фигур, которые они самостоятельно должны рассмотреть и
Слайд 11Первым будет самый простой вариант (первый рисунок), обычная криволинейная трапеция, как в определении.
1 тип
Слайд 12Во втором варианте наша фигура будет ограничена не осью абсцисс, а другой функцией g(x).
Поскольку границы интегрирования здесь одинаковые, то это всё можно записать под одним интегралом (смотрите формулы под рисунком) всё зависит от сложности функций, в каком случае проще будет найти интеграл.
2 тип
Слайд 13Третий очень похож к первому, но только наша трапеция размещена, не над осью
3тип
Слайд 14И четвёртый вариант, когда часть нашей фигуры находится над осью абсцисс, а часть
4 тип
Слайд 15Мы рассмотрели наиболее простые варианты, но теперь вернемся к нашей задаче.
Площадь криволинейной
У любого определенного интеграла (который существует) есть очень хороший геометрический смысл.
Слайд 16Рассмотрим наш рисунок, который похож на те, что мы рассмотрели. На
Слайд 17Начнём с функции f(x) здесь нам надо искать интеграл от a до b, но при этом
Если взять функцию g(x), то видим, что она нам поможет найти площадь части фигуры, которая расположена под осью абсцисс, не забываем про знак минус для этой части интеграла. Также помним, что мы должны были вычесть один из уголков, который расположен под графиком этой функции. Поэтому в нас выходит интеграл со знаком минус от функции g(x)с границами от a до d.
Следующей возьмём функцию v(x), видим, что здесь надо брать интеграл от b до c. Но видим, что наша фигура ограничивается не осью OX, а функцией u(x) поэтому надо ещё вычесть ту часть плоскости, которая попадает в этот интервал [b; c] и расположена между осью OX и графиком функции u(x).
И последней рассмотрим функцию u(x), видим, что она нам поможет найти вторую часть фигуры, что расположена нижеоси абсцисс, а также помним, что мы должны вычесть ту часть площади, которая находится между осью OX и графиком функции u(x) до с. Поэтому, как и со второй функцией будем иметь интеграл со знаком минус, но теперь от функции u(x) и с границами от d до c.
Слайд 19Вспомогательные вопросы для преподавателя к обсуждению и оцениванию студентов
Задавая вопросы, преподаватель
Слайд 20
Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие?
Какие у
Вы сами сталкивались когда-либо с подобной проблемой?
Воспользовались бы Вы сами подсказками и советами со стороны?
Что хотят проверить составители подобных заданий?
Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?
Какая литература была использована?
Кто принимал решение в вашей группе?
Какие варианты решения имел тот, кто принимал решение?
Была ли на него возложена основная работа?
Справились ли вы с поставленной целью в решении конкретной задачи?






![Пример кейса по математике:Задача о трапеции Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной, неотрицательной функции f(x) Криволинейной трапецией называется фигура, которая ограничена графиком непрерывной, неотрицательной функции f(x) на промежутке [a;b], отрезками прямых x=a](/img/thumbs/09f3b91652c85ea8bad755a2b6196096-800x.jpg)