- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по решению задач Объём призмы
Содержание
- 1. Презентация урока по решению задач Объём призмы
- 2. Цель урока:обучить решению задач на вычисление объема
- 3. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
- 4. Слайд 4
- 5. ОСНОВНЫЕ ТЕРМИНЫБоковые ребра призмы Боковую поверхность
- 6. ОБЪЕМ ПРИЗМЫТеорема. Объем призмы равен произведению площади
- 7. Основанием прямой треугольной призмы служит прямоугольный треугольник
- 8. Задача №2Гранью параллелепипеда является ромб со стороной
- 9. Задача №3В сосуд, имеющий форму правильной треугольной
- 10. Задача №4Через среднюю линию основания треугольной призмы
- 11. Задача №5 Объём куба равен 12. Найдите
- 12. Задача№6. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной
- 13. Задача №7 Найдите объем призмы, в основаниях
- 14. Основание прямой призмы –квадрат, а ее боковые
- 15. Решение задачи№8
- 16. Самостоятельная работа 1.В сосуд, имеющий форму правильной
- 17. ДОМАШНЕЕ ЗАДАНИЕГлава 2,§3№ 11,№ 14,
- 18. МБОУ «Сатинская СОШ»Урок подготовила учитель математикиГорбунова Ольга Егоровна2017 уч. год
Цель урока:обучить решению задач на вычисление объема призм, обобщить и систематизировать имеющиеся у учащихся сведения о призме и ее элементах, формировать умения решать задачи повышенной сложности;развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение
Слайд 2Цель урока:
обучить решению задач на вычисление объема призм, обобщить и систематизировать
имеющиеся у учащихся сведения о призме и ее элементах, формировать умения решать задачи повышенной сложности;
развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;
выработать привычку к постоянной занятости каким- либо полезным делом, воспитание отзывчивости, трудолюбия, аккуратности.
развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;
выработать привычку к постоянной занятости каким- либо полезным делом, воспитание отзывчивости, трудолюбия, аккуратности.
Слайд 5 ОСНОВНЫЕ ТЕРМИНЫ
Боковые ребра призмы
Боковую поверхность призмы.
Высоту призмы.
Прямую призму.
Наклонную
призму.
Правильную призму.
Диагональное сечение призмы.
Диагональ призмы.
Перпендикулярное сечение призмы.
Площадь боковой поверхности призмы.
Площадь полной поверхности призмы.
Объем призмы.
Правильную призму.
Диагональное сечение призмы.
Диагональ призмы.
Перпендикулярное сечение призмы.
Площадь боковой поверхности призмы.
Площадь полной поверхности призмы.
Объем призмы.
Слайд 6ОБЪЕМ ПРИЗМЫ
Теорема.
Объем призмы равен произведению площади основания на высоту.
Следствие.
Объем
прямой призмы равен произведению площади основания на длину бокового ребра:V=Sосн∙b (Sосн -площадь основания, b- длина бокового ребра)
Слайд 7Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и
8, боковое ребро равно 5. Найдите объем призмы.
Задание 8 № 27082
Задача №1
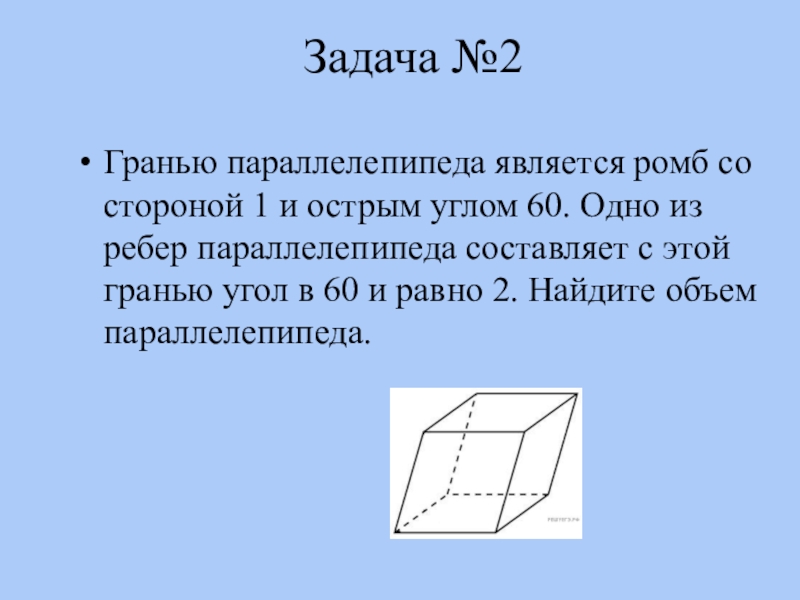
Слайд 8Задача №2
Гранью параллелепипеда является ромб со стороной 1 и острым углом
60. Одно из ребер параллелепипеда составляет с этой гранью угол в 60 и равно 2. Найдите объем параллелепипеда.
Слайд 9Задача №3
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень
воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
Слайд 10Задача №4
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому
ребру. Найдите объём этой призмы, если объём отсеченной треугольной призмы равен 5.
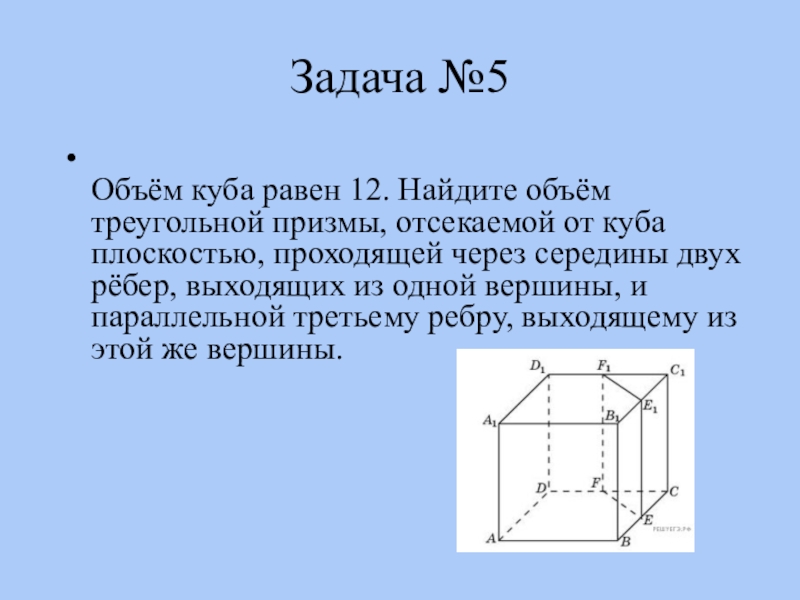
Слайд 11Задача №5
Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от
куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
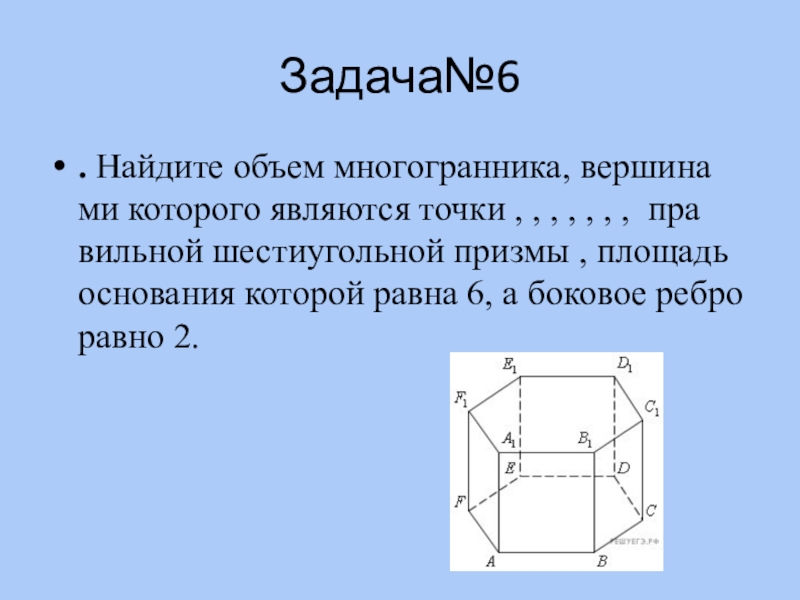
Слайд 12Задача№6
. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания
которой равна 6, а боковое ребро равно 2.
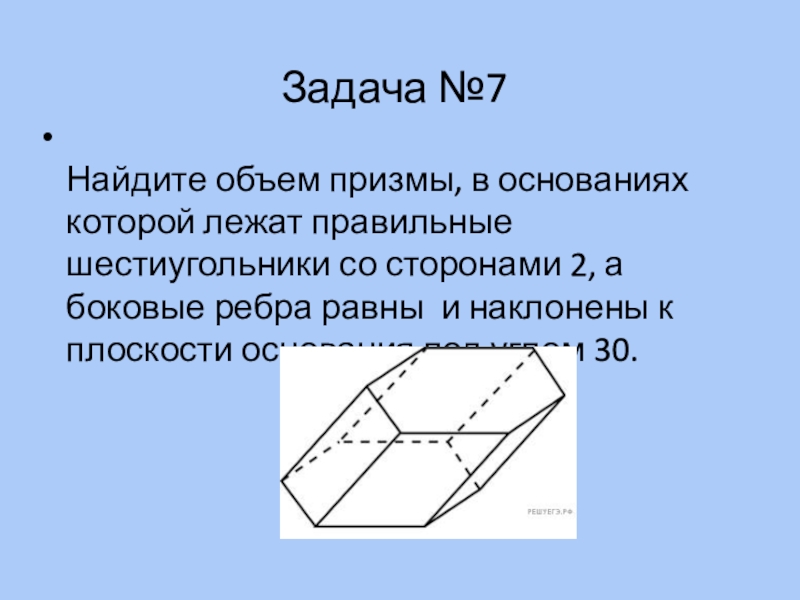
Слайд 13Задача №7
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со
сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом 30.
Слайд 14Основание прямой призмы –квадрат, а ее боковые ребра в два раза
больше стороны основания. Вычислите объем призмы, если радиус окружности, описанной около сечения призмы плоскостью, проходящей через сторону основания и середину противолежащего бокового ребра, равен 2√3 см.
Задача №8.
Слайд 16Самостоятельная работа
1.В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень
воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
2. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10
2. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10