Елена Михайловна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Треугольники
Содержание
- 1. Презентация по теме Треугольники
- 2. Урок 1 «Первый признак равенства треугольников»Урок 2
- 3. Урок 1 «Первый признак равенства треугольников»
- 4. Жили-были три подружки В разных домиках своих.
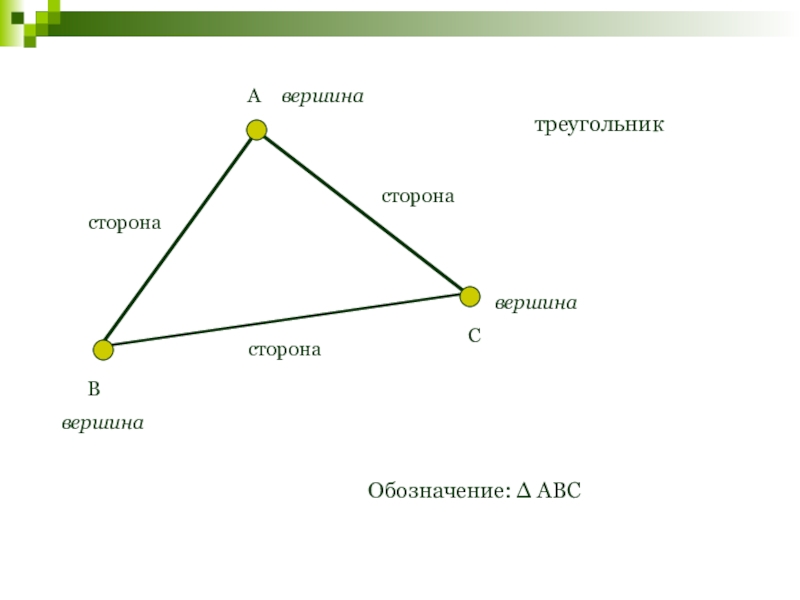
- 5. треугольникАВСвершинавершинавершинасторонасторонасторонаОбозначение: ∆ АВС
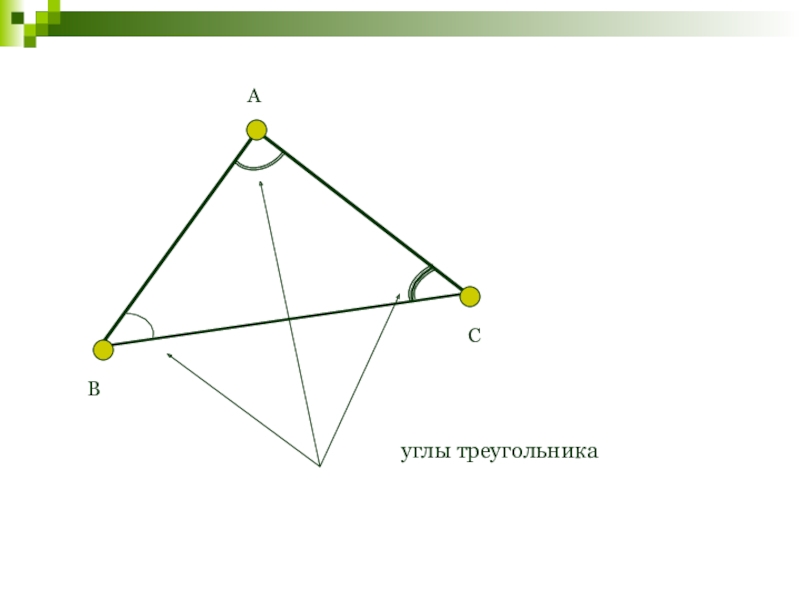
- 6. АВСуглы треугольника
- 7. Исправьте ошибки, которые допустил Незнайка.Любой треугольник составлен
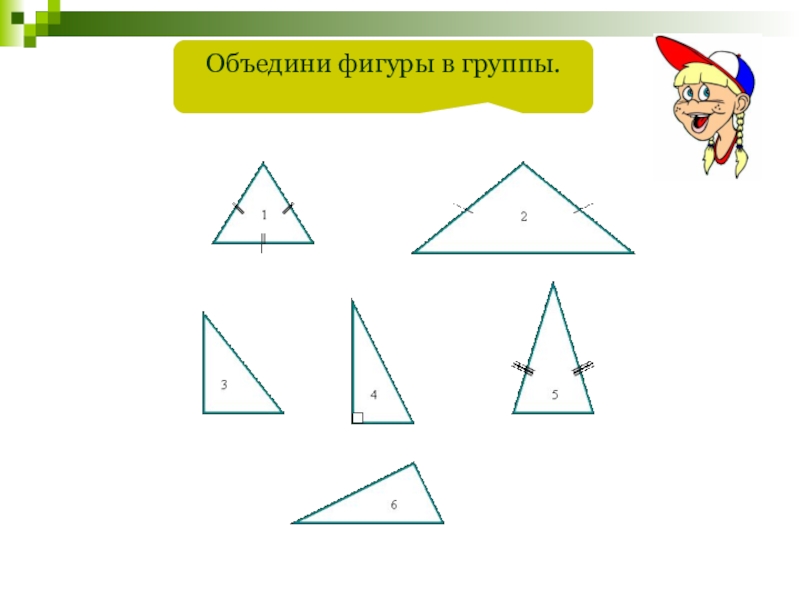
- 8. Найдите среди данных фигур треугольники.123456
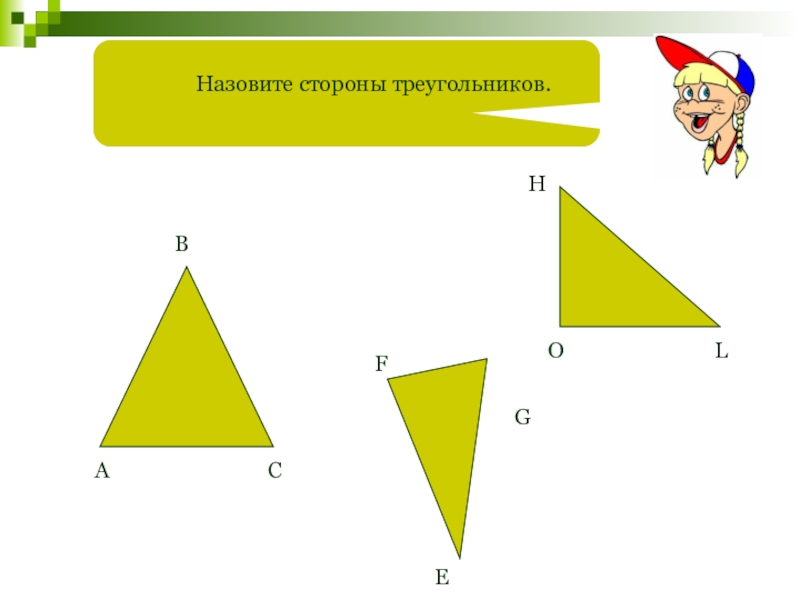
- 9. Назовите стороны треугольников.АВCFEGHOL
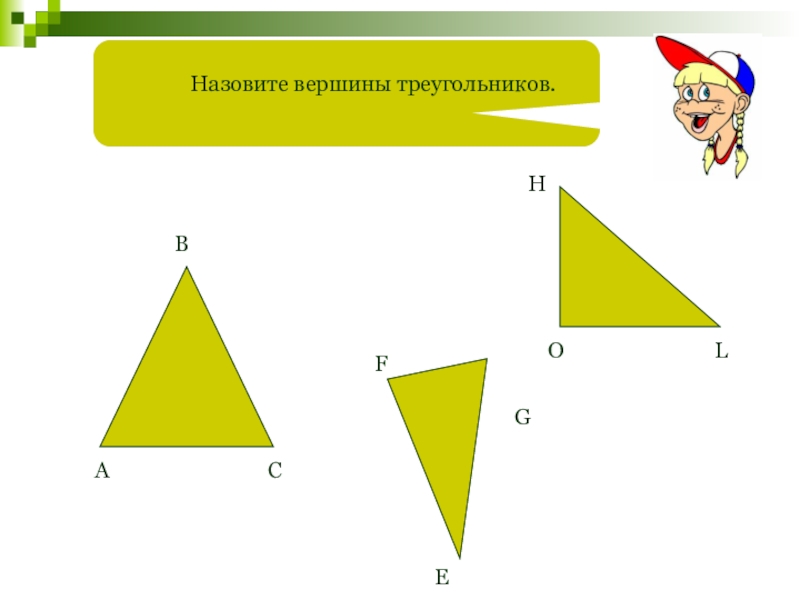
- 10. Назовите вершины треугольников.АВCFEGHOL
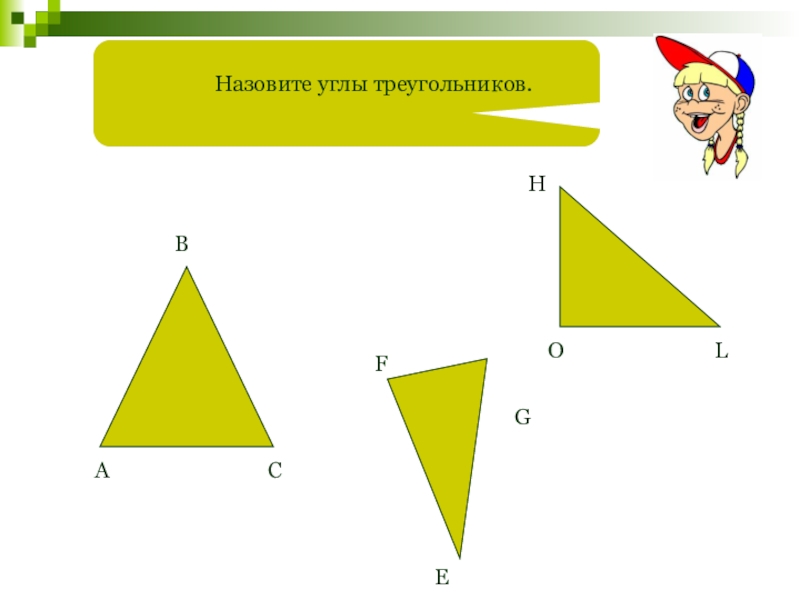
- 11. Назовите углы треугольников.АВCFEGHOL
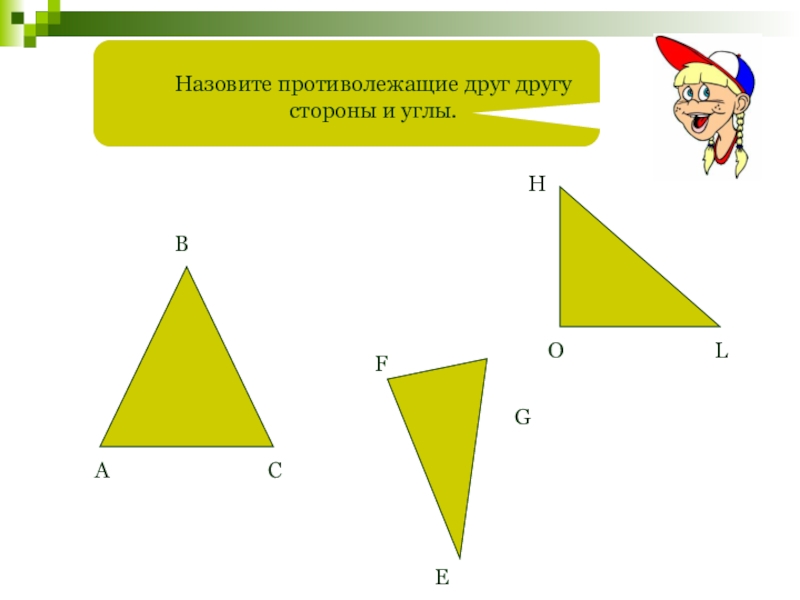
- 12. Назовите противолежащие друг другу стороны и углы.АВCFEGHOL
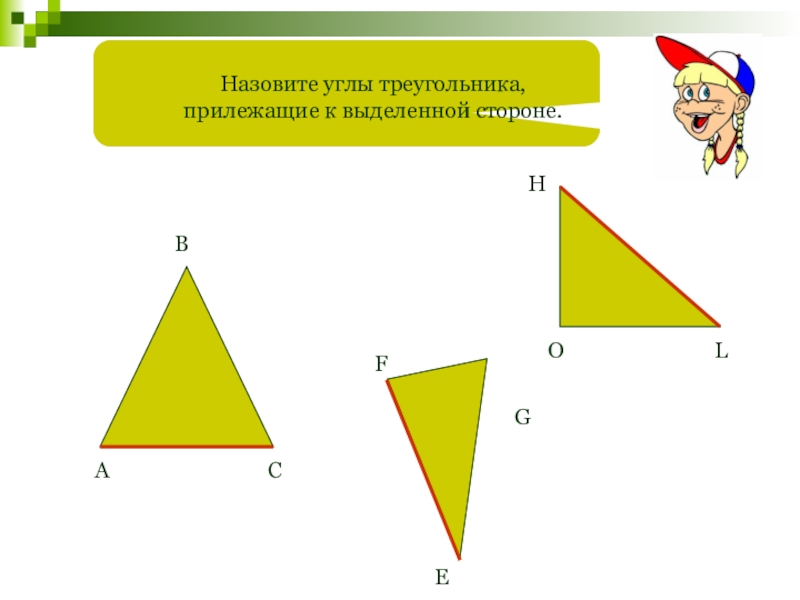
- 13. Назовите углы треугольника, прилежащие к выделенной стороне.АВCFEGHOL
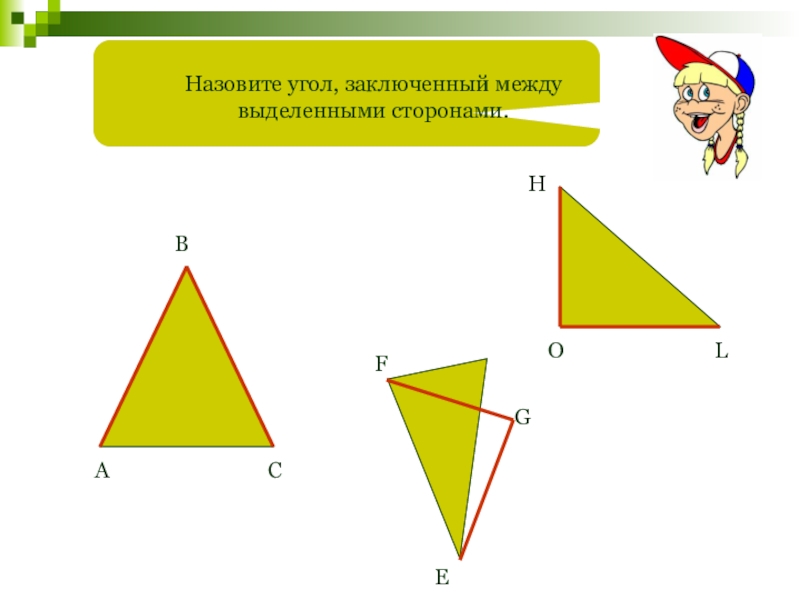
- 14. Назовите угол, заключенный между выделенными сторонами.АВCFEGHOL
- 15. Выполните в тетради следующие задания:Начертите треугольник АВС
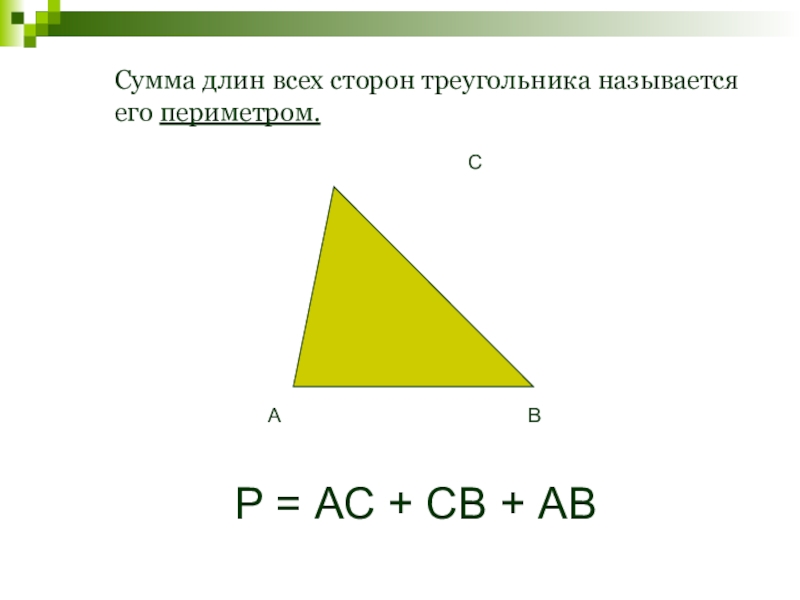
- 16. Сумма длин всех сторон треугольника называется его периметром.АВСР = АС + СВ + АВ
- 17. Периметр одного треугольника больше периметра другого треугольника. Могут быть равными эти треугольники?
- 18. Два треугольника называются равными, если их можно совместить наложением.
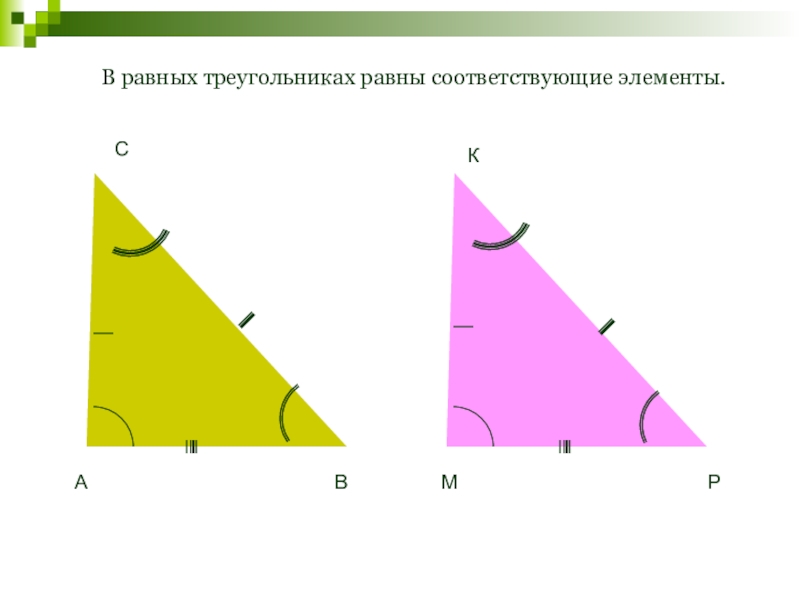
- 19. В равных треугольниках равны соответствующие элементы.АВСМКР
- 20. Назовите равные элементы в треугольниках.АВСМКРGHVXYZ
- 21. Выполните в тетради следующие задания:№ 92∆АВС =
- 22. Домашнее задание:§ 1, пункт 14, стр. 28№ 89 а№ 90
- 23. Урок 2 «Первый признак равенства треугольников»
- 24. Подготовьте ответы на следующие вопросы:Какая фигура называется
- 25. Утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой.Рассуждения называются доказательством теоремы.
- 26. Первый признак равенства треугольников.Если две стороны и
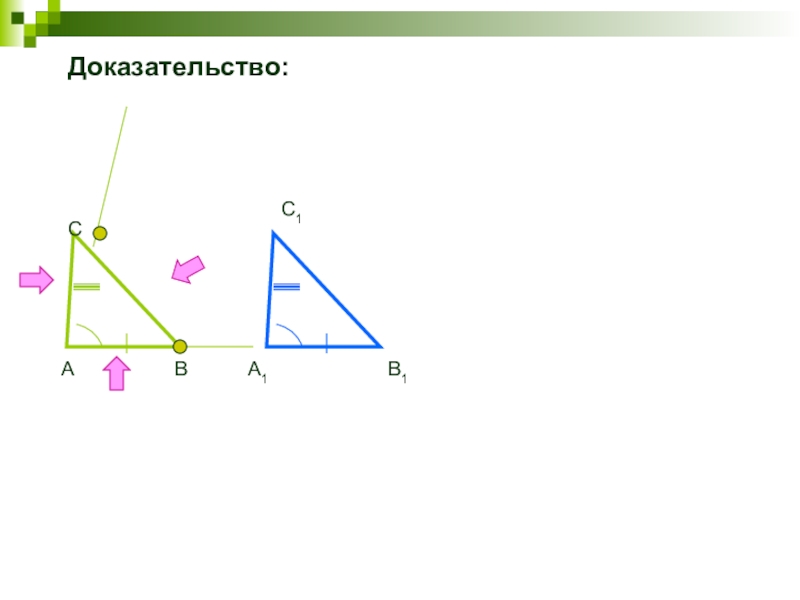
- 27. Доказательство:АВСА1С1В1
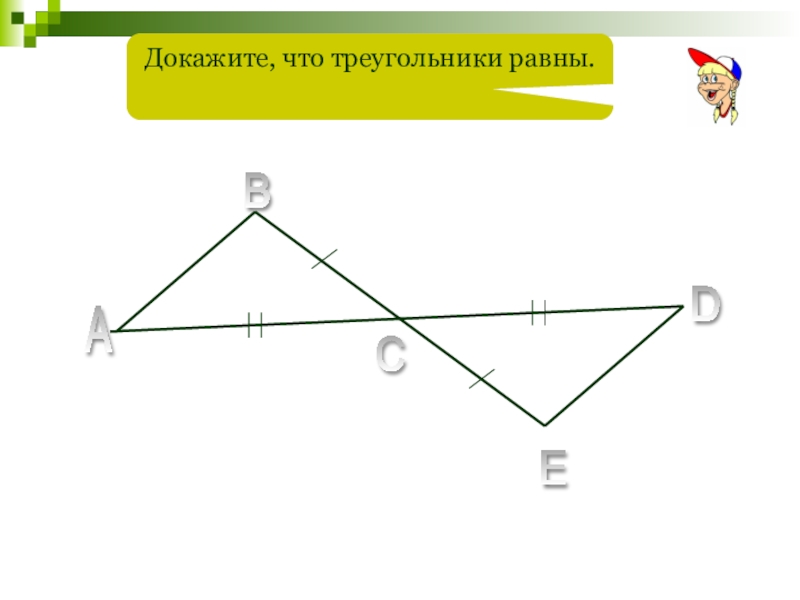
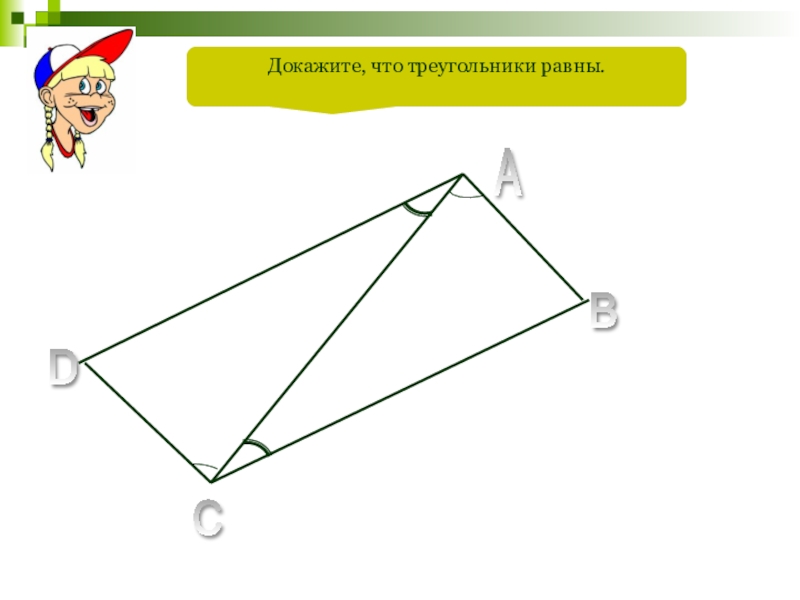
- 28. A B C D E Докажите, что треугольники равны.
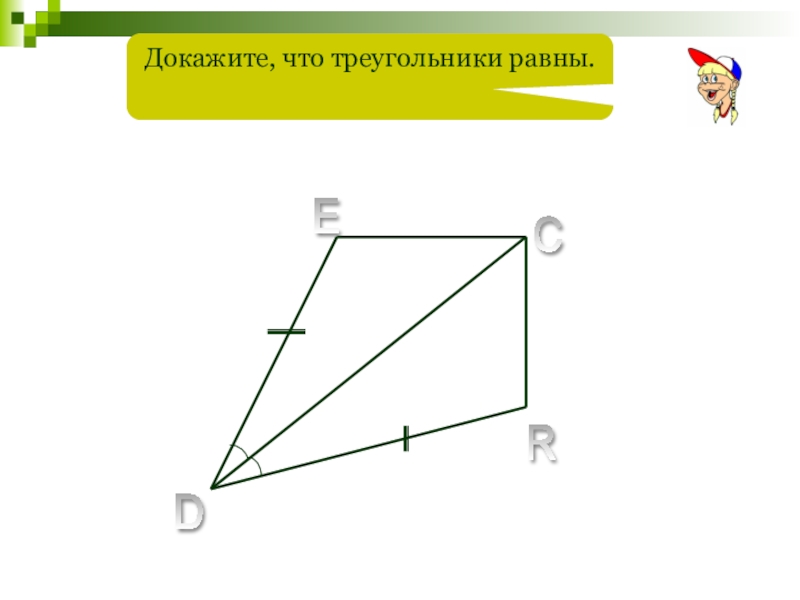
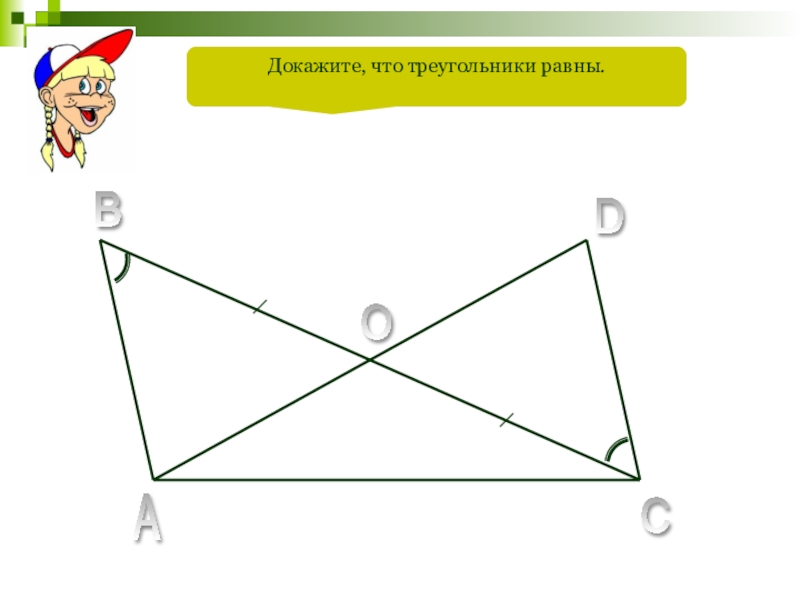
- 29. D E C R Докажите, что треугольники равны.
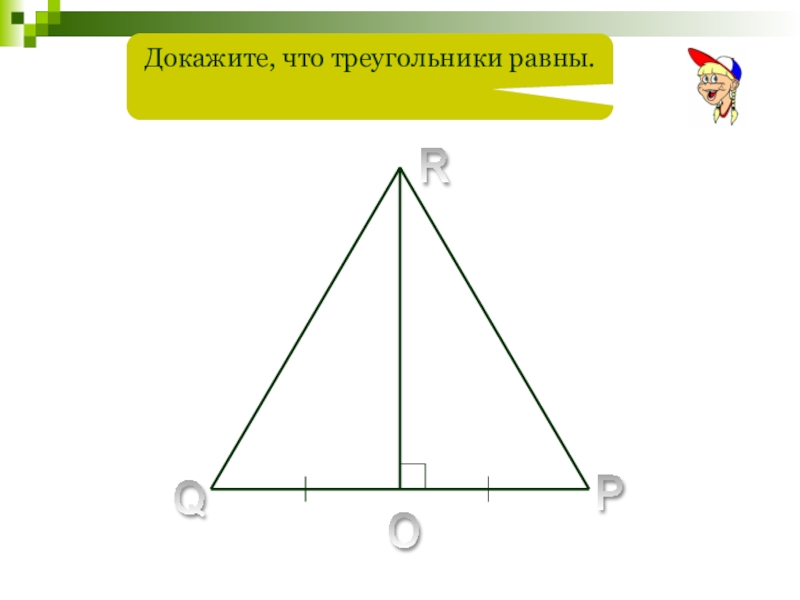
- 30. R P O Q Докажите, что треугольники равны.
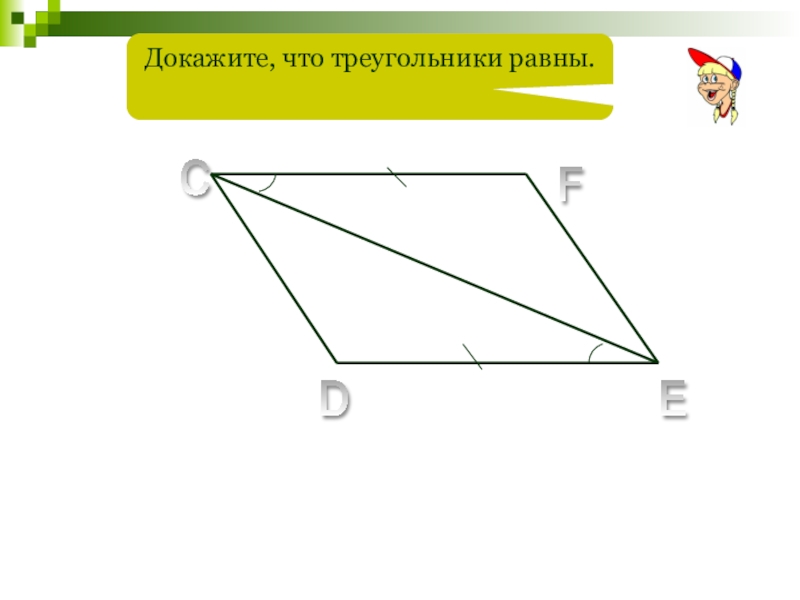
- 31. D C F E Докажите, что треугольники равны.
- 32. Решите в тетради следующие задачи:№ 93 а№ 94
- 33. Домашнее задание:§ 1, пункт 15, стр. 28№ 96№ 97
- 34. Урок 3 «Первый признак равенства треугольников»
- 35. Подготовьте ответы на следующие вопросы:Что называют теоремой?Что называют доказательством теоремы?Сформулируйте и докажите первый признак равенства треугольников.
- 36. Прочти ребус:
- 37. Объедини фигуры в группы.
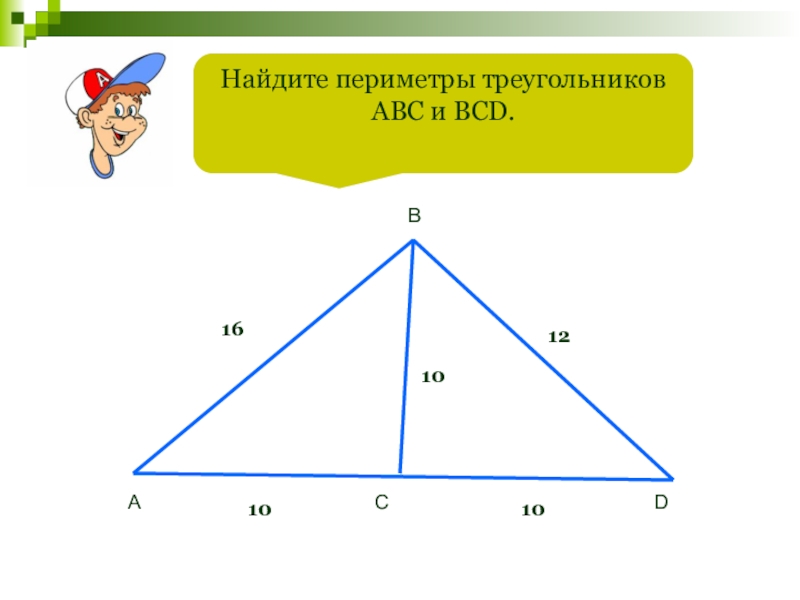
- 38. Найдите периметры треугольников АВС и ВСD.АСDB1610101012
- 39. Решите следующие задачи:Периметр треугольника равен 40 м.
- 40. Самостоятельная работа.Докажите равенство треугольников и найдите углы ADC, ACD.12ADCB38°102°ADBC108°32°
- 41. Домашнее задание:№ 98№ 99
- 42. Урок 4 «Медианы, биссектрисы и высоты треугольника»
- 43. АаНперпендикуляр, проведенный из точки А к прямой аоснование перпендикуляра
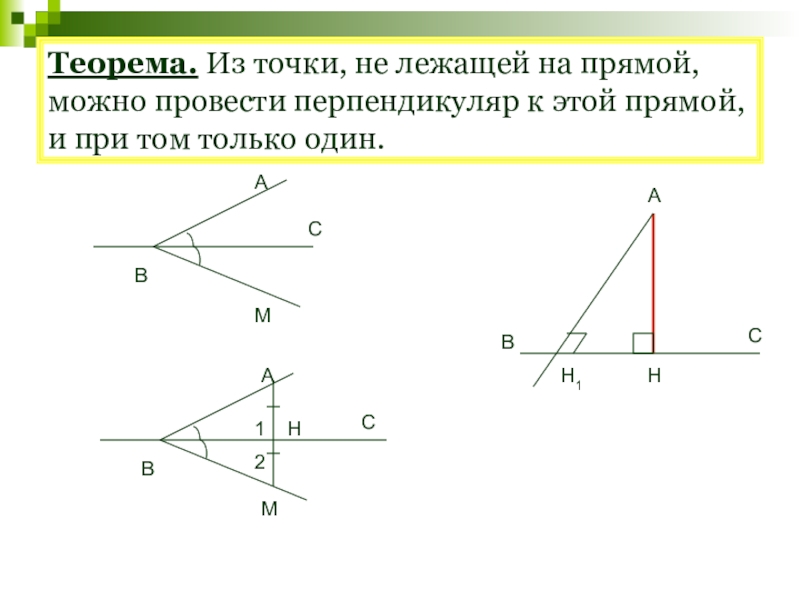
- 44. Теорема. Из точки, не лежащей на прямой,
- 45. Выполните в тетради:№100№105
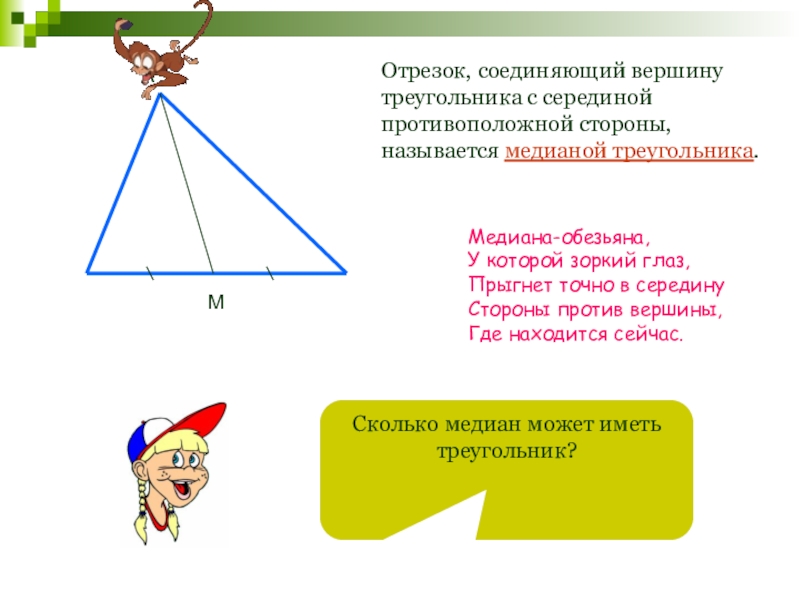
- 46. АМОтрезок, соединяющий вершину треугольника с серединой противоположной
- 47. АМОтрезок биссектрисы угла треугольника, соединяющий вершину треугольника
- 48. АНПерпендикуляр, проведенный из вершины треугольника к прямой,
- 49. Убедитесь на практике в том, что в
- 50. Выполните в тетради:№101№102№103
- 51. Домашнее задание:№ 104№ 106Пункт 16 – 17 учить.
- 52. Урок 5 «Медианы, биссектрисы и высоты треугольника»
- 53. Подготовьте ответы на следующие вопросы:Что называют перпендикуляром,
- 54. Треугольник называется равнобедренным, если две его стороны равны.боковая сторонабоковая сторонаоснование
- 55. Треугольник называется равносторонним, если все его стороны равны.
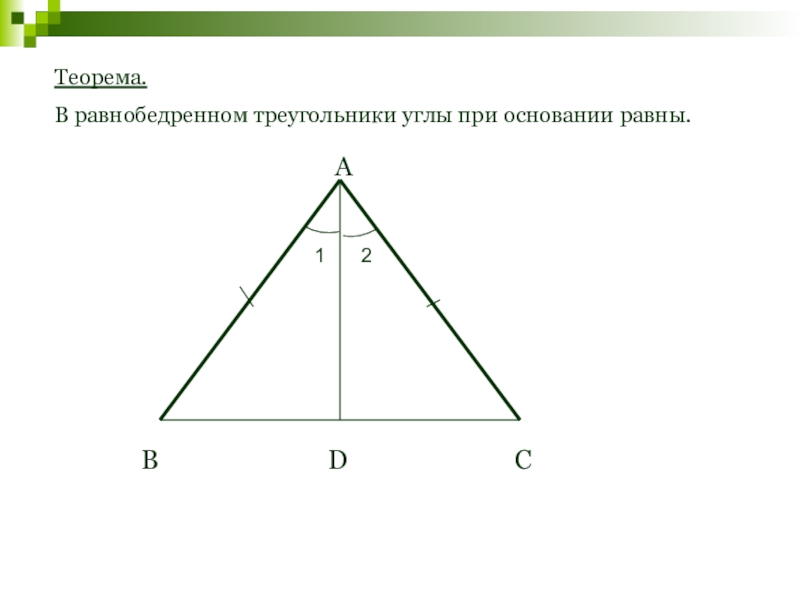
- 56. Теорема.В равнобедренном треугольники углы при основании равны.12ВСDА
- 57. Теорема.В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.12ВСDА34
- 58. Медиана равнобедренного треугольника, проведенная к основанию, является
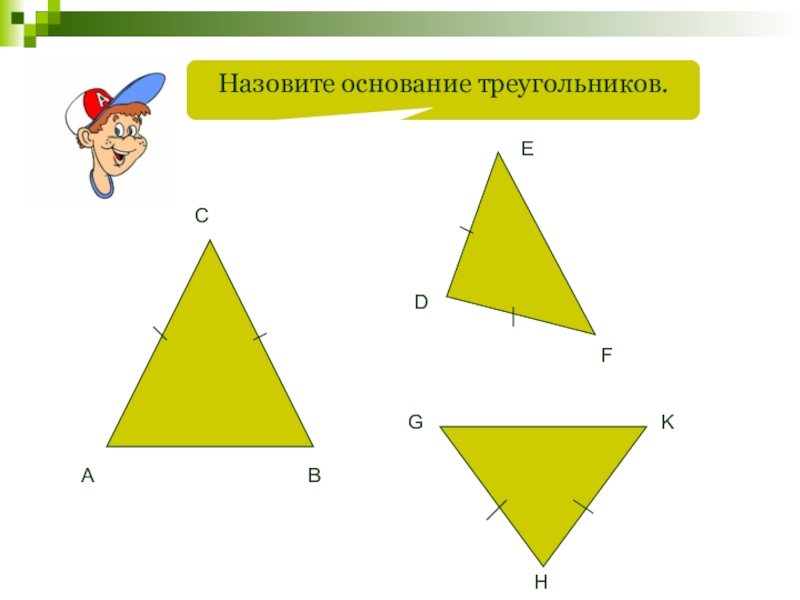
- 59. Назовите основание треугольников.ABCDEFGHK
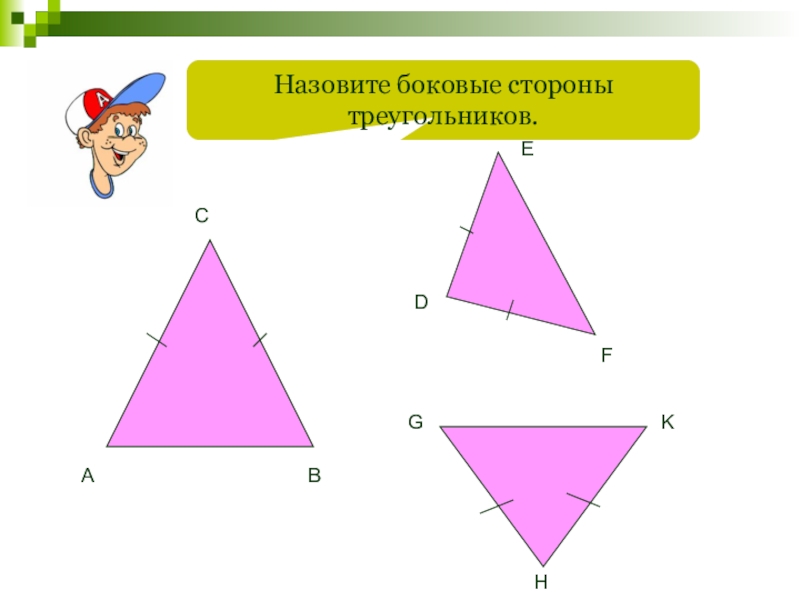
- 60. Назовите боковые стороны треугольников.ABCDEFGHK
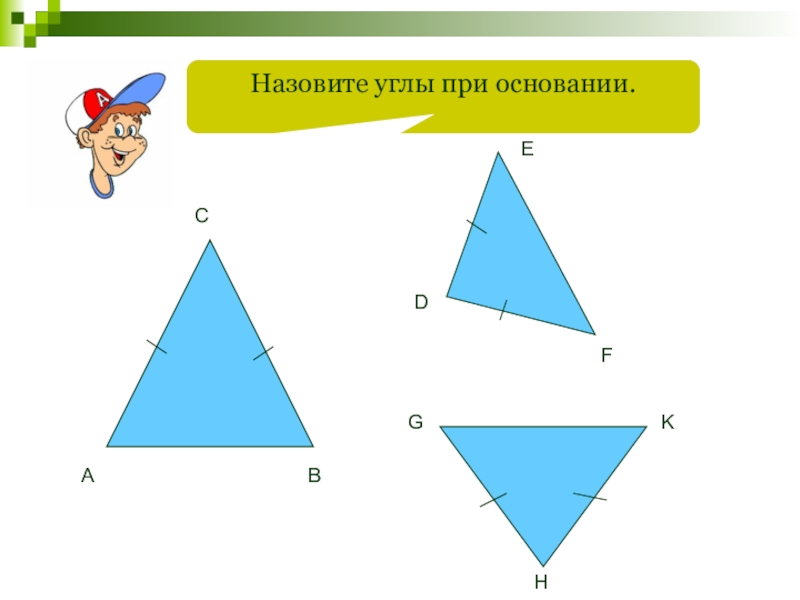
- 61. Назовите углы при основании.ABCDEFGHK
- 62. Назовите угол, противолежащий основанию.ABCDEFGHK
- 63. 6719 20 21 8519 20 21 2аа5а
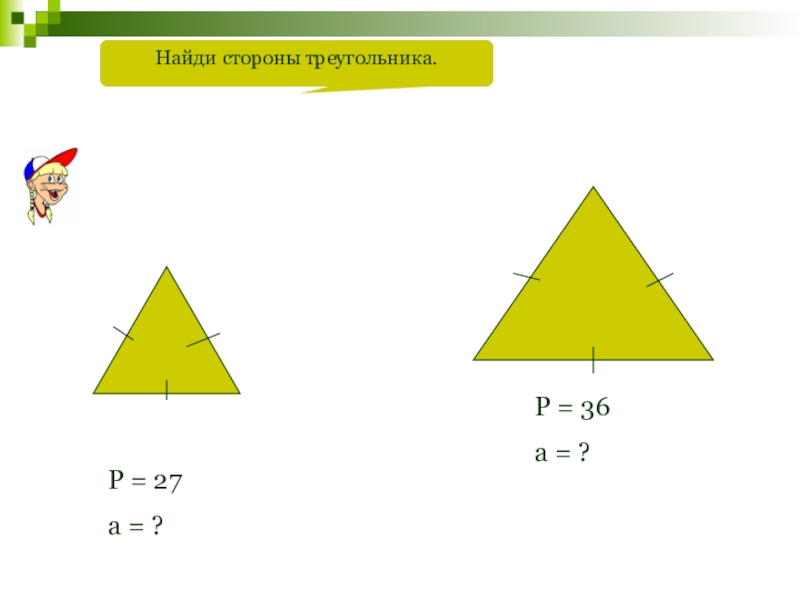
- 64. Найди стороны треугольника.Р = 27а = ?Р = 36а = ?
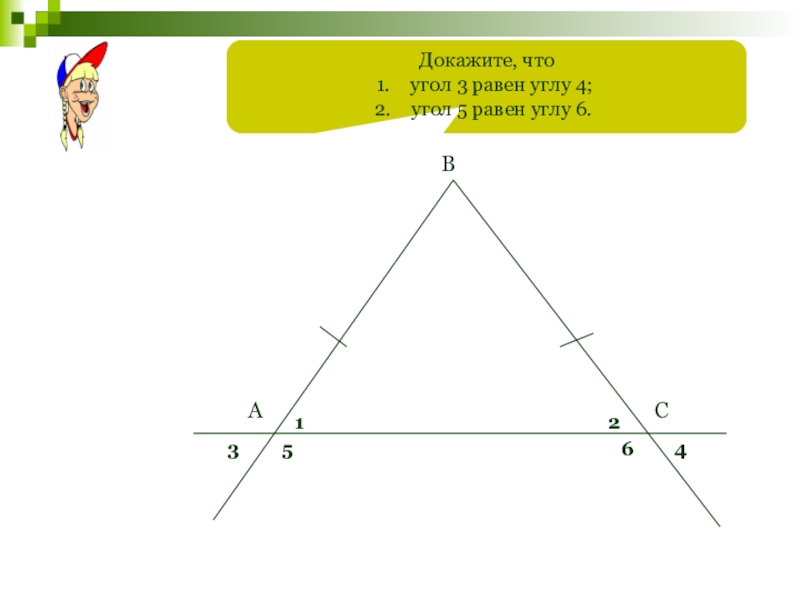
- 65. Докажите, чтоугол 3 равен углу 4;угол 5 равен углу 6.АВС123564
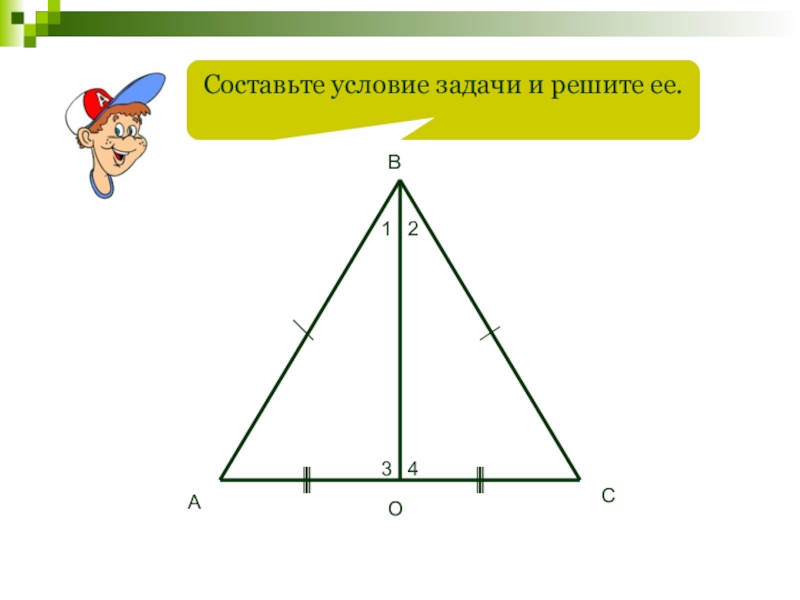
- 66. Составьте условие задачи и решите ее.АВСО1234
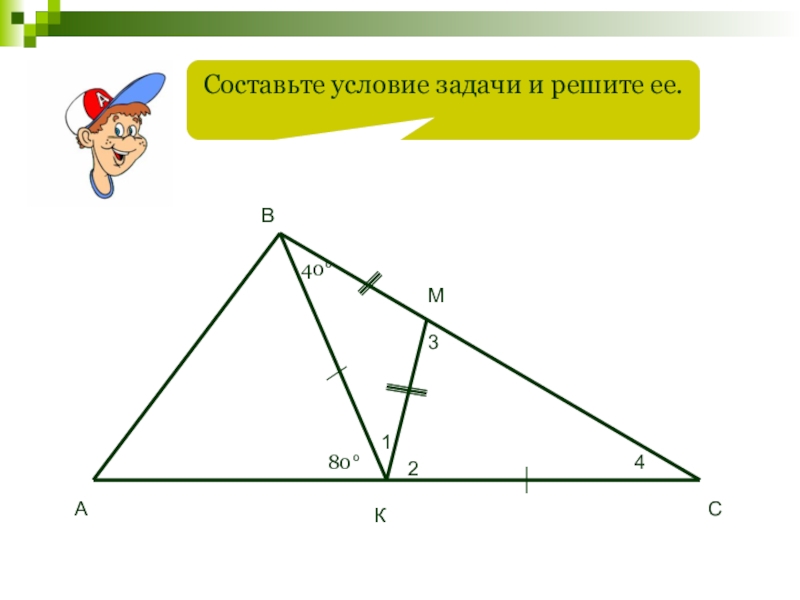
- 67. Составьте условие задачи и решите ее.40°80°1234АВСКМ
- 68. Домашнее задание:№ 107№ 111№ 112
- 69. Урок 6 «Медианы, биссектрисы и высоты треугольника»
- 70. Подготовьте ответы на следующие вопросы:Какой треугольник называется равнобедренным?Как называются стороны равнобедренного треугольника?Какой треугольник называется равносторонним?
- 71. Незнайка доказал теорему о свойстве углов при
- 72. А теорему о биссектрисе равнобедренного треугольника доказал
- 73. Сыграем?Щелкни по мячу, находящемуся в равнобедренном треугольнике.5574а4а5а3а4а5а88,27,97а4а+3а9с
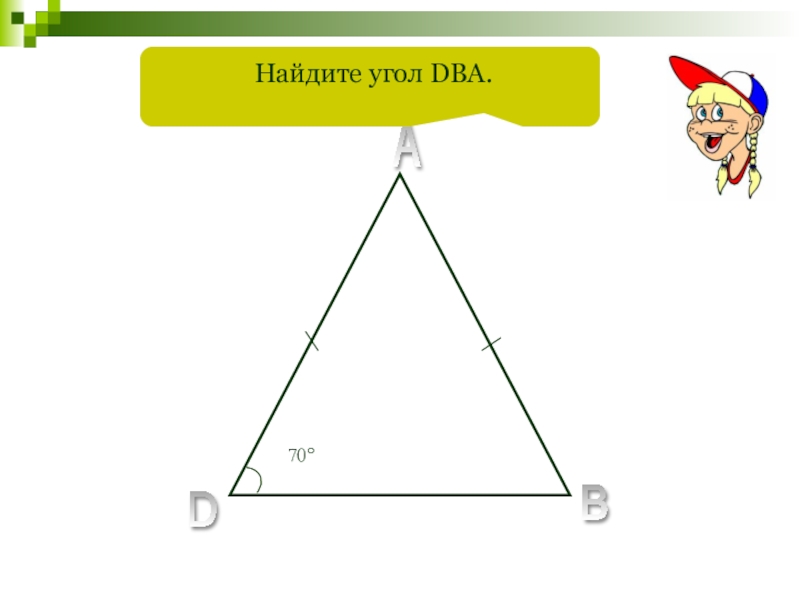
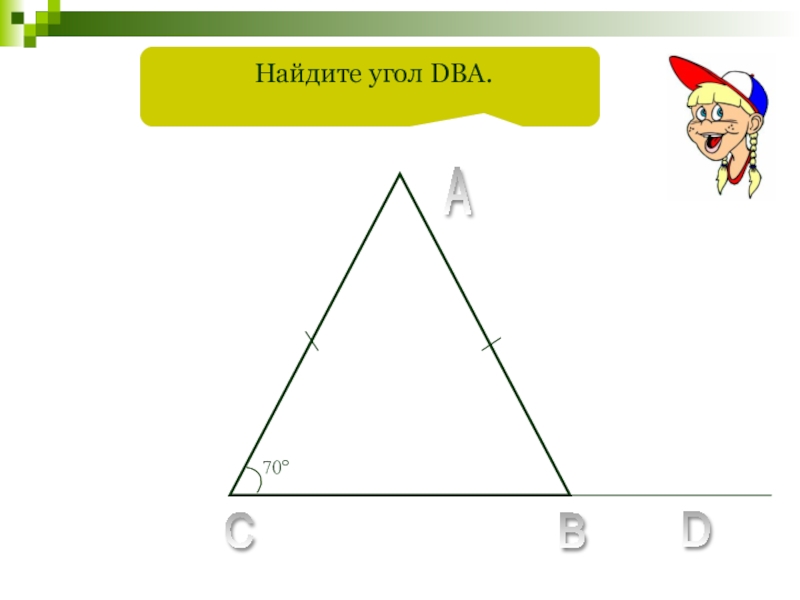
- 74. 70°A B D Найдите угол DBA.
- 75. 70°A B C D Найдите угол DBA.
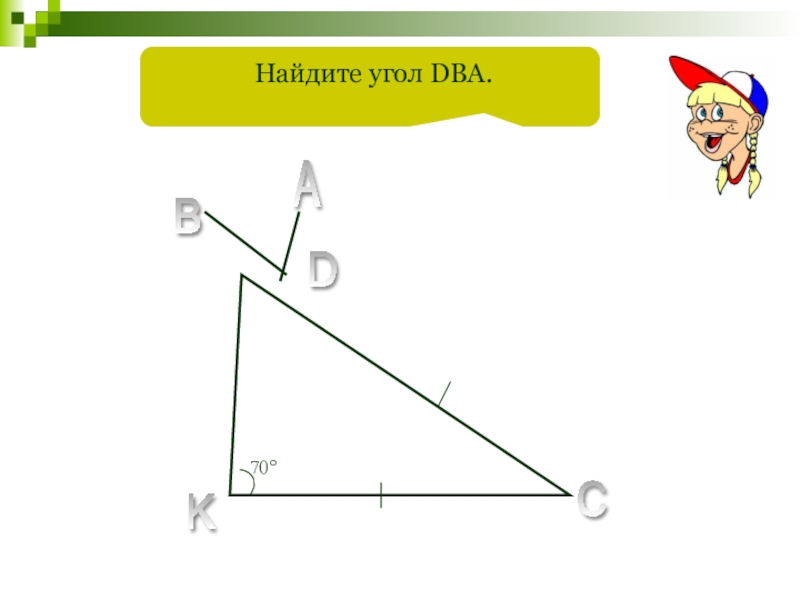
- 76. 70°A B C K D Найдите угол DBA.
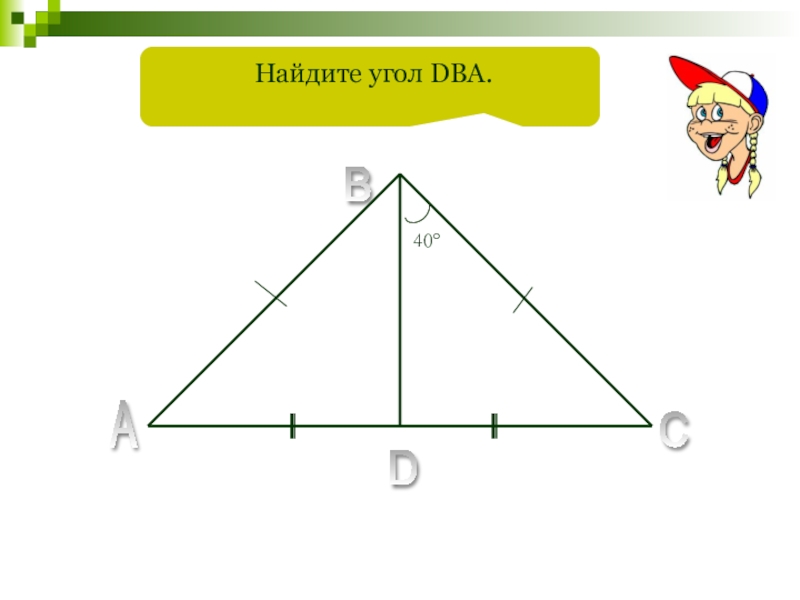
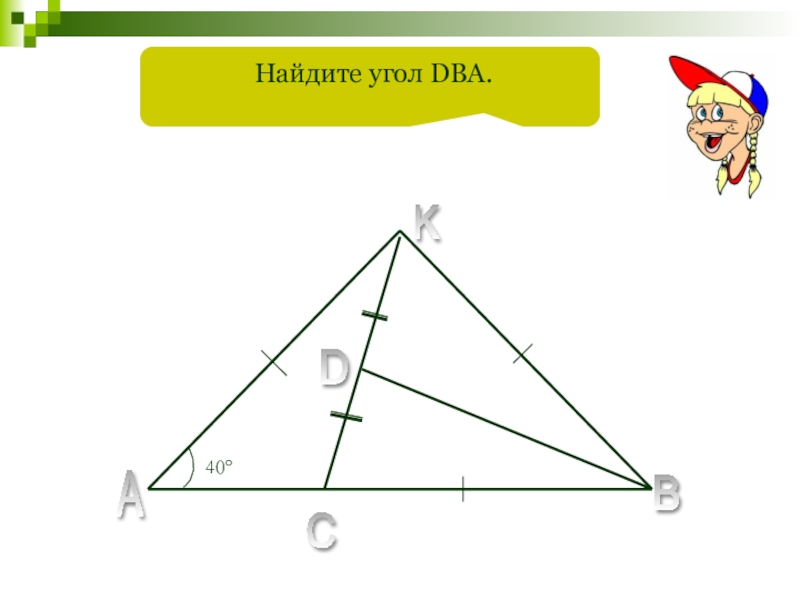
- 77. 40°A B C D Найдите угол DBA.
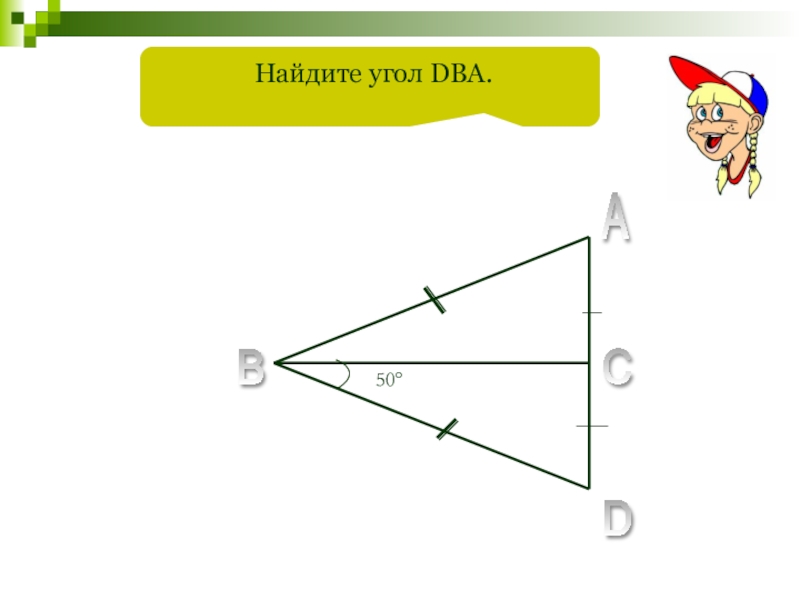
- 78. A B C D 50°Найдите угол DBA.
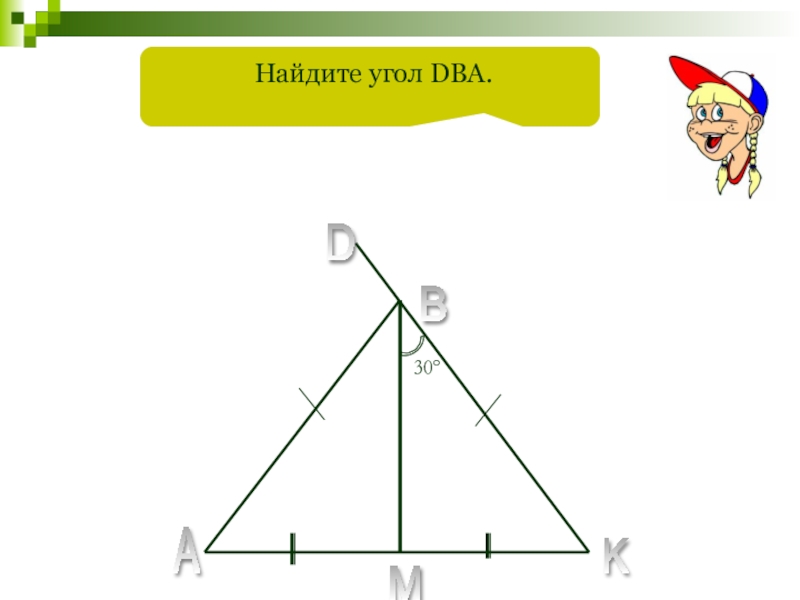
- 79. 30°A B D C M K Найдите угол DBA.
- 80. 30°A B D M K Найдите угол DBA.
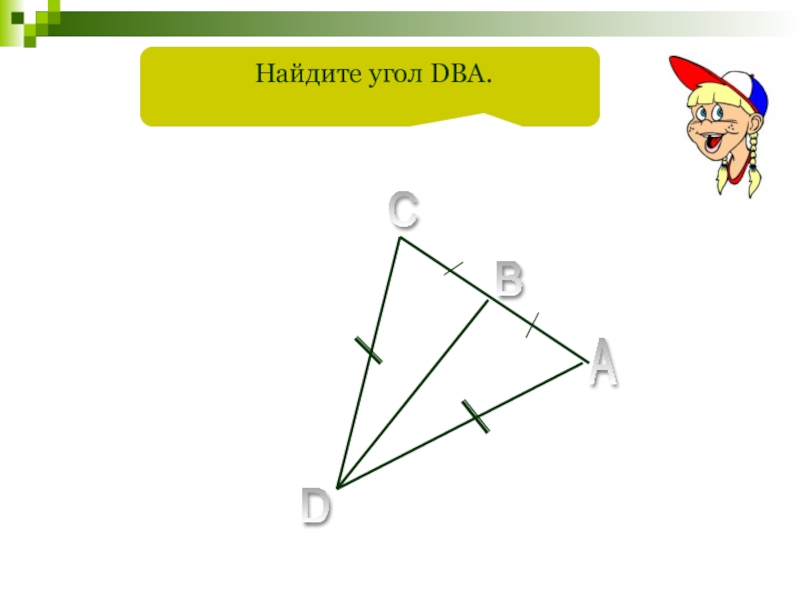
- 81. D C B A Найдите угол DBA.
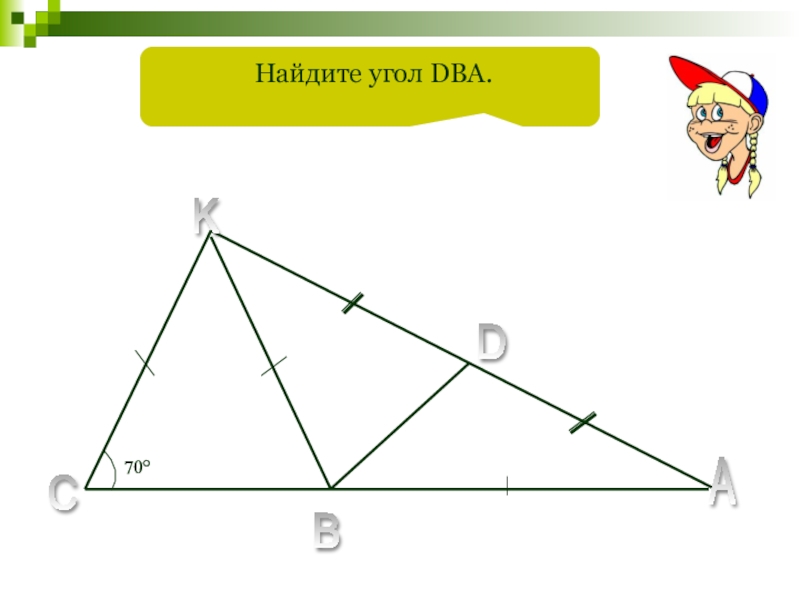
- 82. 70°C K D A B Найдите угол DBA.
- 83. 40°A C B D K Найдите угол DBA.
- 84. Самостоятельная работа.В равнобедренном треугольнике сумма всех углов
- 85. Домашнее задание:№ 115№ 117№ 120 б
- 86. Урок 7 «Второй и третий признаки равенства треугольников»
- 87. Математический диктант.Перпендикуляр к прямой – это …Сколько
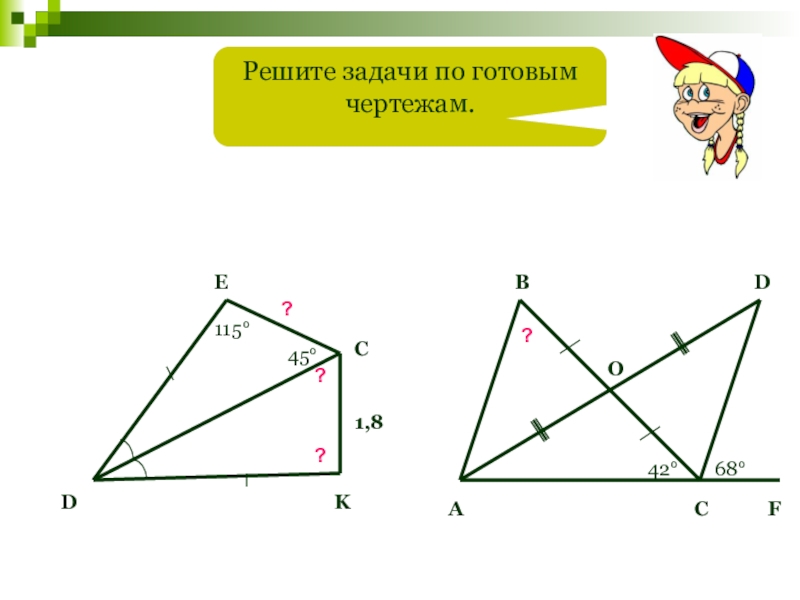
- 88. Решите задачи по готовым чертежам.DECK??1,8?45°115°АBODCF42°68°?
- 89. С помощью транспортира и масштабной линейки начертите
- 90. Теорема.Если сторона и два прилежащих к ней
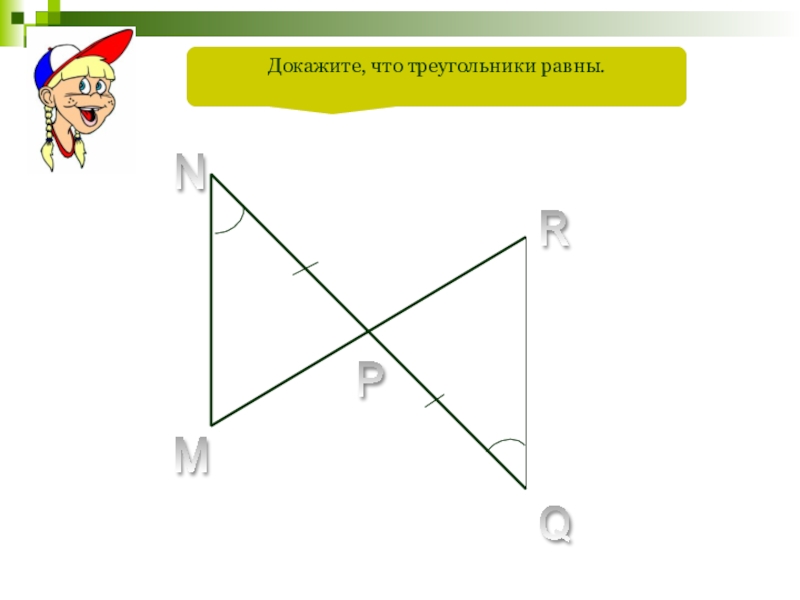
- 91. N M R Q P Докажите, что треугольники равны.
- 92. A B C D Докажите, что треугольники равны.
- 93. Докажите, что треугольники равны.A B C D O
- 94. Решите в тетради № 121№ 123
- 95. Среди пяти слов одно «лишнее»,найдите его.
- 96. Домашнее задание:№ 122№ 124 выучить доказательство 2 признака равенства треугольников
- 97. Урок 8 «Второй и третий признаки равенства треугольников»
- 98. Сформулируйте и докажите 2 признак равенства треугольников.
- 99. A B C D O Укажите равные треугольники на этом рисунке.
- 100. Решите задачи:№ 126№ 132
- 101. Самостоятельная работа.Отрезки МК и ВО пересекаются в
- 102. Домашнее задание:№ 129№ 132
- 103. Урок 11 «Задачи на построение».
- 104. Ребята, что в вашем понимании значит слово
- 105. У каждого понятия есть содержание:Содержание понятия –
- 106. Для каждого понятия можно указать его объем:Объем
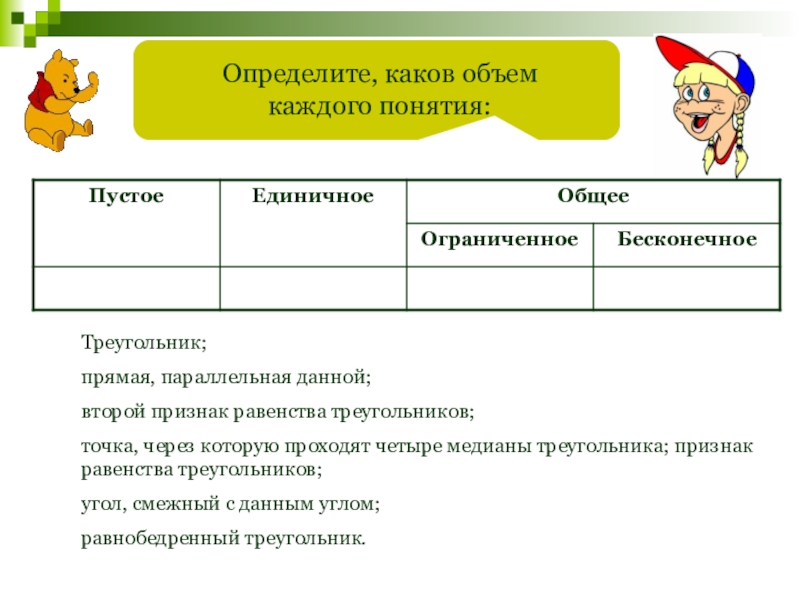
- 107. Определите, каков объем каждого понятия:Треугольник; прямая, параллельная
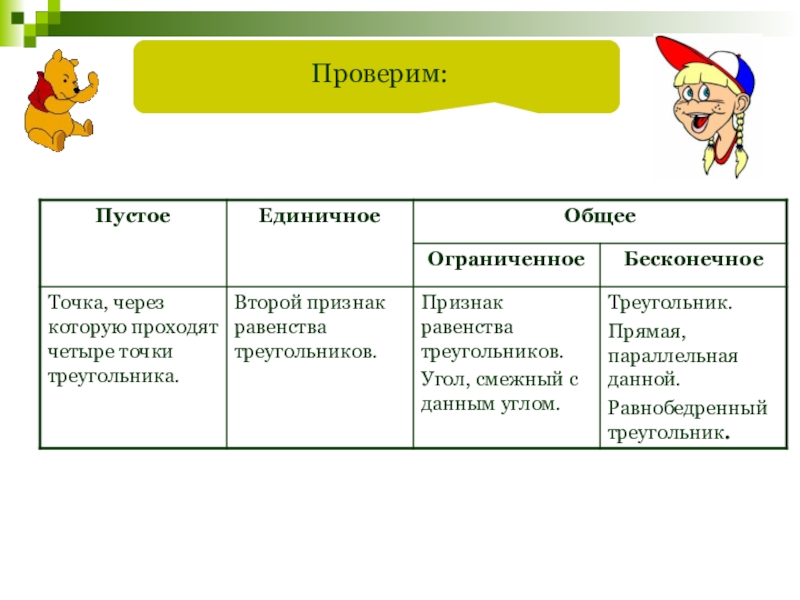
- 108. Проверим:
- 109. Когда вы решаете задачу, отвечаете на вопросы
- 110. А теперь мы узнаем, что такое определение:Определение
- 111. Познакомимся с рядом определений:Окружностью называется геометрическая фигура,
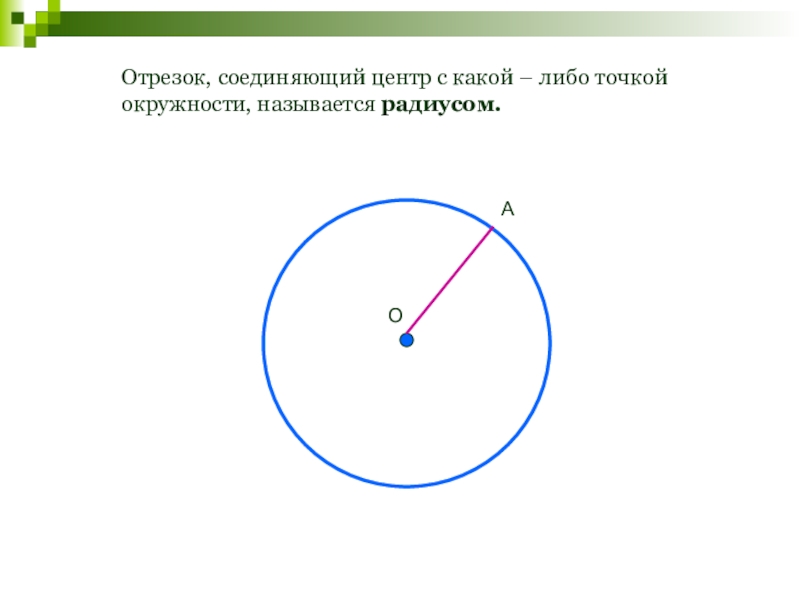
- 112. Отрезок, соединяющий центр с какой – либо точкой окружности, называется радиусом.ОА
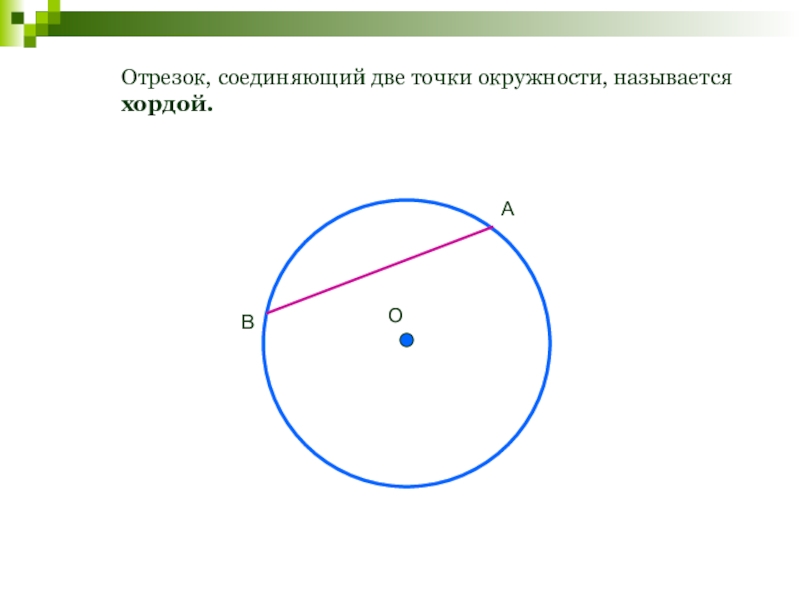
- 113. Отрезок, соединяющий две точки окружности, называется хордой.ОАВ
- 114. Хорда, проходящая через центр окружности, называется диаметром.ОАВ
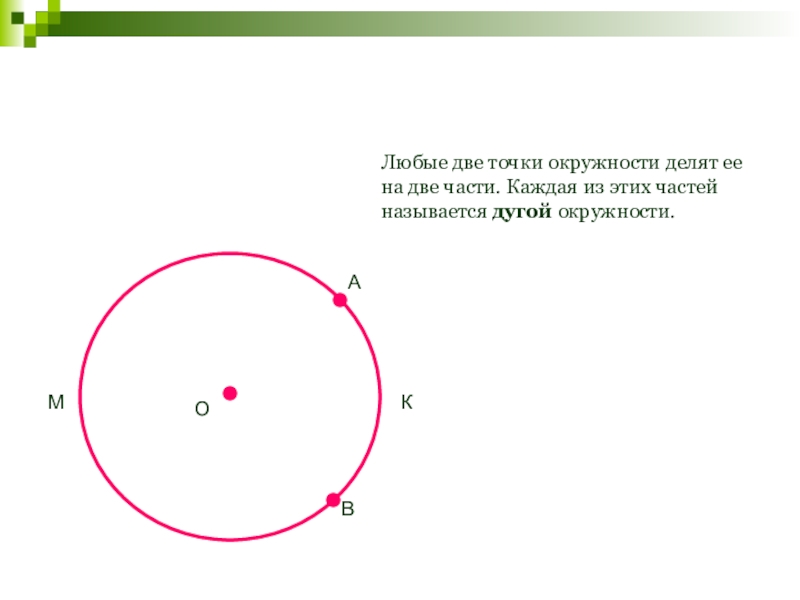
- 115. ОАВ Любые две точки окружности делят ее
- 116. Часть плоскости, ограниченная окружностью, называется кругом.
- 117. Назовите радиусы, хорды, диаметры окружности.OADCVNMLS
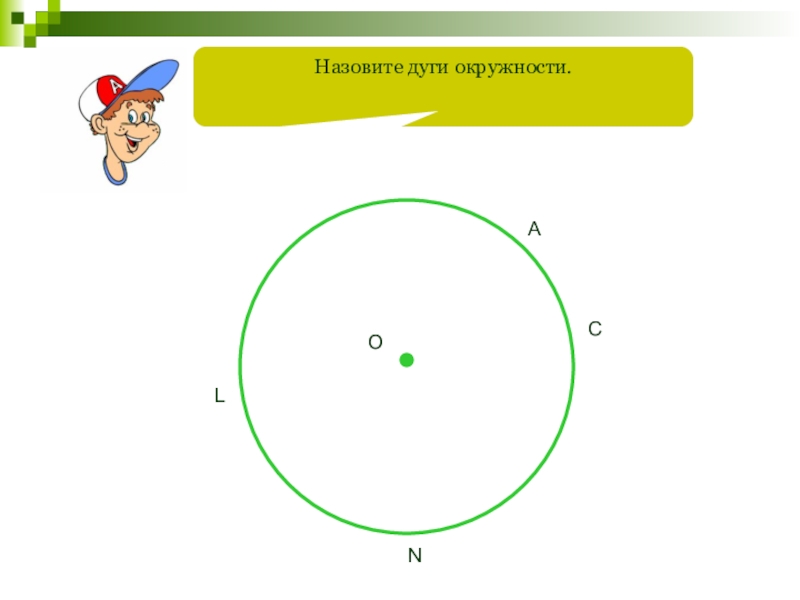
- 118. Назовите дуги окружности.OACNL
- 119. Прочитайте чертеж.Докажите, что BD = AC.OABCD
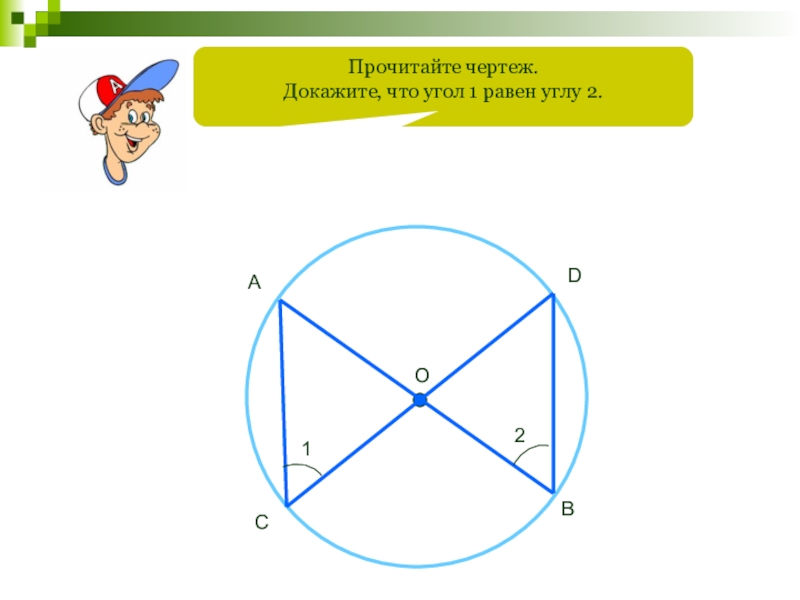
- 120. Прочитайте чертеж.Докажите, что угол 1 равен углу 2.OABCD12
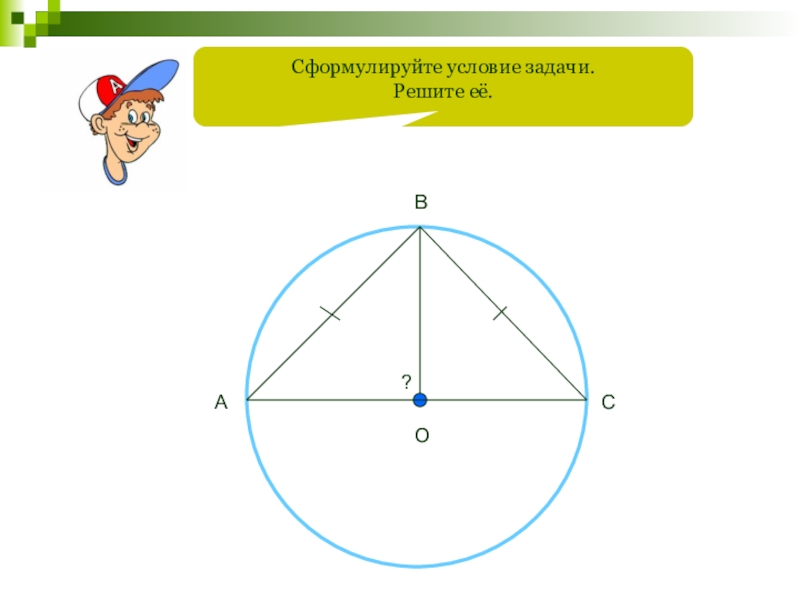
- 121. Сформулируйте условие задачи.Решите её.OABC?
- 122. Решите в тетради № 146.
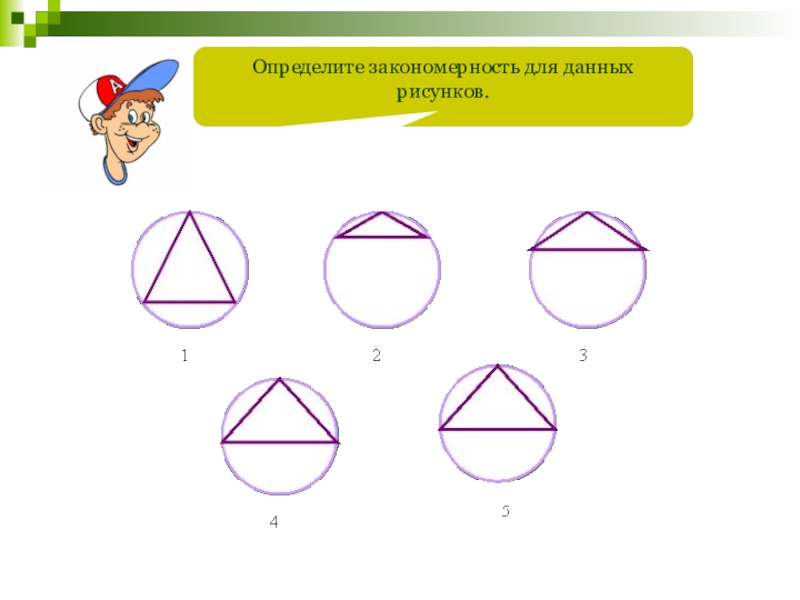
- 123. Определите закономерность для данных рисунков.
- 124. Разгадайте ребус.
- 125. Домашнее задание:§ 4 пункт 21№ 147№ 156№ 157
- 126. Урок 12 «Задачи на построение»
- 127. Ответьте на следующие вопросы:Что такое определение понятия?Дайте
- 128. Самостоятельная работа.1 вариантОтрезки КМ и EF являются
- 129. Сегодня мы научимся решать задачи на построение:
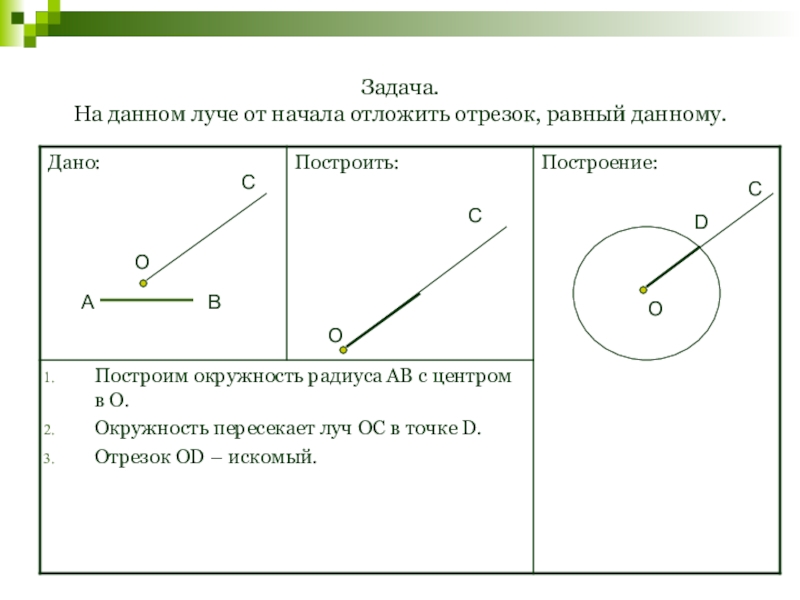
- 130. Задача. На данном луче от начала отложить отрезок, равный данному.ОСDОСАВОС
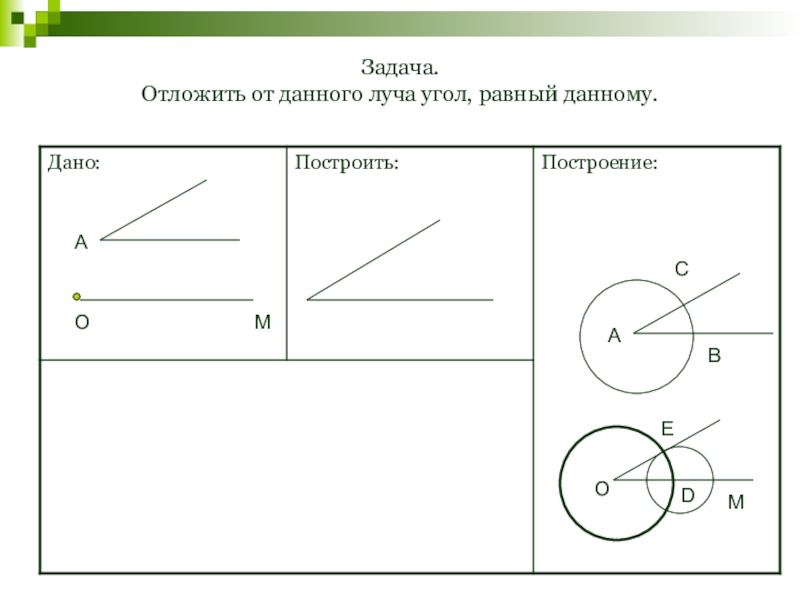
- 131. Задача. Отложить от данного луча угол, равный данному.АОМАСВОЕMD
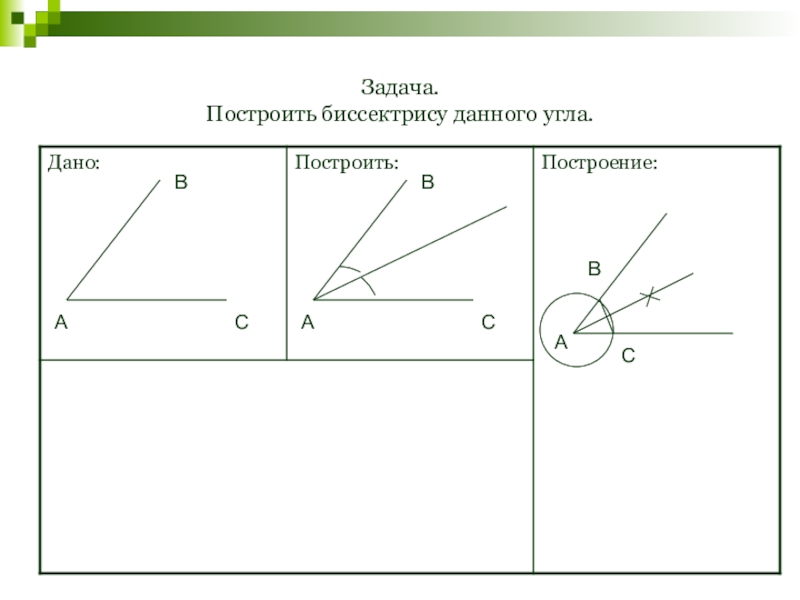
- 132. Задача. Построить биссектрису данного угла.АВСАВСАВС
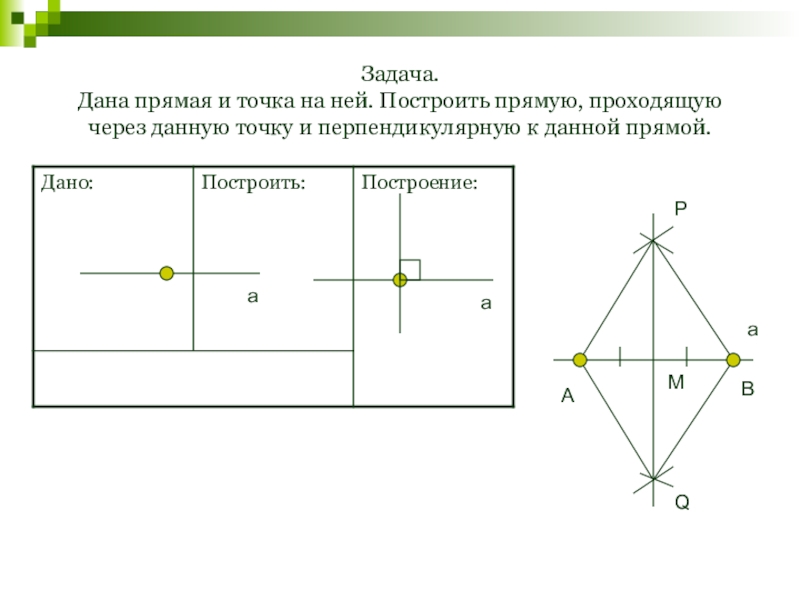
- 133. Задача. Дана прямая и точка на ней.
- 134. Задача. Построить середину данного отрезка.АВАВОАВРQО12
- 135. Домашнее задание:§ 4 пункты 22-23 выучить
- 136. Урок 15 «Решение задач»
- 137. Сегодня на уроке мы побываем в царстве Треугольников.
- 138. Царство треугольников Царство треугольников состоит из четырех
- 139. Первой областью правит царь Наитупейшее Величество.Как вы
- 140. Второй областью правит царица Высота.Дайте определение высоты треугольника.Начертите в тетради тупоугольный треугольник и постройте его высоты.
- 141. Третьей областью правит царица Медиана. Дайте определение
- 142. Четвертой областью правит царица Биссектриса. Дайте определение
- 143. В царстве Треугольников был издан Свод законов,
- 144. Урок 16 «Подготовка к контрольной работе»
- 145. Продолжите фразы:Треугольником называется …Треугольник обозначается …Высотой треугольника
- 146. Установите соответствие:Определение равных треугольников.Первый признак равенства треугольников.Второй
- 147. В следующем задании щелкните по правильным ответам, и вы увидите картинку.Решение задач оформите в тетради.
- 148. АВСТреугольники равны:по 1 признакупо 2 признакупо 3
Урок 1 «Первый признак равенства треугольников»Урок 2 «Первый признак равенства треугольников»Урок 3 «Первый признак равенства треугольников»Урок 4 «Медианы, биссектрисы и высоты треугольника»Урок 5 «Медианы, биссектрисы и высоты треугольника»Урок 6 «Медианы, биссектрисы и высоты треугольника»Урок 7 «Второй
Слайд 1Треугольники
Геометрия, 7 класс
Подготовила: учитель математики МОУ СОШ №4 с.Новомихайловског о
Иова
Слайд 2Урок 1 «Первый признак равенства треугольников»
Урок 2 «Первый признак равенства треугольников»
Урок
3 «Первый признак равенства треугольников»
Урок 4 «Медианы, биссектрисы и высоты треугольника»
Урок 5 «Медианы, биссектрисы и высоты треугольника»
Урок 6 «Медианы, биссектрисы и высоты треугольника»
Урок 7 «Второй и третий признаки равенства треугольников»
Урок 8 «Второй и третий признаки равенства треугольников»
Урок 11 «Задачи на построение»
Урок 12 «Задачи на построение»
Урок 15 «Решение задач»
Урок 16 «Подготовка к контрольной работе»
Урок 4 «Медианы, биссектрисы и высоты треугольника»
Урок 5 «Медианы, биссектрисы и высоты треугольника»
Урок 6 «Медианы, биссектрисы и высоты треугольника»
Урок 7 «Второй и третий признаки равенства треугольников»
Урок 8 «Второй и третий признаки равенства треугольников»
Урок 11 «Задачи на построение»
Урок 12 «Задачи на построение»
Урок 15 «Решение задач»
Урок 16 «Подготовка к контрольной работе»
Слайд 4
Жили-были три подружки
В разных домиках своих.
Три веселых хохотушки –
Точками все
звали их.
Между этими домами
Реки длинные текли.
Точки очень не хотели
Ножки промочить свои.
И тогда они решили
Между домиками взять
Сделать мостики большие,
Чтобы в гости прибегать.
Мост с мостом соединился,
Что же, в общем, получился?
Слайд 7
Исправьте ошибки, которые допустил Незнайка.
Любой треугольник составлен из трех прямых.
Ни
в одном из треугольников нет ни одной прямой.
.
Любой треугольник состоит из трех отрезков.
Любой треугольник состоит из трех отрезков, соединяющих три не лежащих на одной прямой точки.
Любой треугольник имеет три угла.
Любой треугольник имеет три вершины.
.
Любой треугольник состоит из трех отрезков.
Любой треугольник состоит из трех отрезков, соединяющих три не лежащих на одной прямой точки.
Любой треугольник имеет три угла.
Любой треугольник имеет три вершины.
Слайд 15Выполните в тетради следующие задания:
Начертите треугольник АВС и проведите отрезок, соединяющий
вершину А с серединой противоположной стороны.
Начертите ∆ MNP. На стороне МР отметьте произвольную точку К и соедините ее с вершиной, противолежащей стороне МР.
№ 87
№ 88
Начертите ∆ MNP. На стороне МР отметьте произвольную точку К и соедините ее с вершиной, противолежащей стороне МР.
№ 87
№ 88
Слайд 17
Периметр одного треугольника больше периметра другого треугольника. Могут быть равными эти
треугольники?
Слайд 21Выполните в тетради следующие задания:
№ 92
∆АВС = ∆MNP, причем угол А
равен углу М, угол В равен углу N, угол С равен углу Р. Найдите стороны ∆MNP, если АВ=7 см, ВС=5см, СА = 3 см.
Слайд 24
Подготовьте ответы на следующие вопросы:
Какая фигура называется треугольником?
Что называют вершинами и
сторонами треугольника?
Что называют периметром треугольника?
Какие треугольники называют равными?
Что можно сказать об соответствующих элементах равных треугольников?
Что называют периметром треугольника?
Какие треугольники называют равными?
Что можно сказать об соответствующих элементах равных треугольников?
Слайд 25
Утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой.
Рассуждения называются доказательством теоремы.
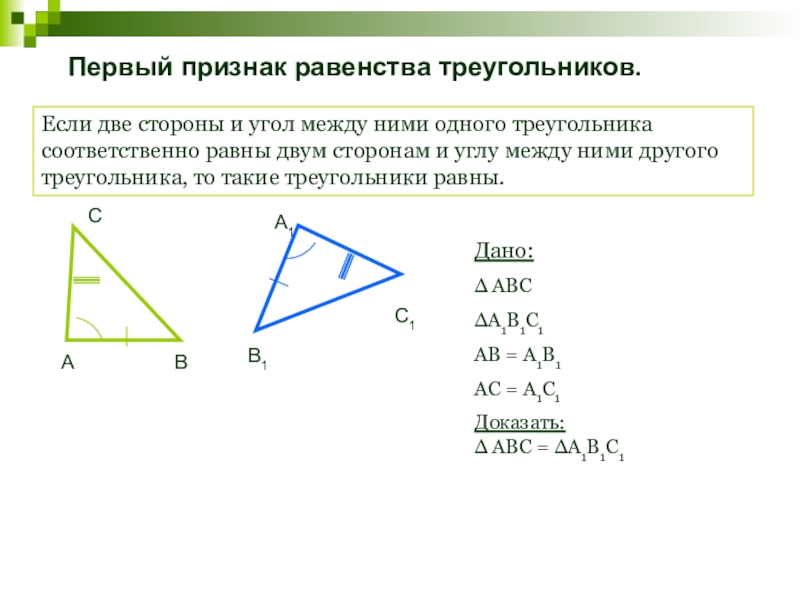
Слайд 26Первый признак равенства треугольников.
Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
А
В
С
А1
С1
В1
Дано:
∆ АВС
∆А1В1С1
АВ = А1В1
АС = А1С1
Доказать:
∆ АВС = ∆А1В1С1
Слайд 35
Подготовьте ответы на следующие вопросы:
Что называют теоремой?
Что называют доказательством теоремы?
Сформулируйте и
докажите первый признак равенства треугольников.
Слайд 39Решите следующие задачи:
Периметр треугольника равен 40 м. Найдите его стороны, если
одна сторона на 4 м меньше второй стороны и на 6 м меньше третьей стороны.
Отрезки ВС и DE пересекаются в точке А. Докажите, что, если А – общая середина отрезков ВС и DE, то ∆АВD=∆АСЕ.
Отрезки ВС и DE пересекаются в точке А. Докажите, что, если А – общая середина отрезков ВС и DE, то ∆АВD=∆АСЕ.
Слайд 40Самостоятельная работа.
Докажите равенство треугольников и найдите углы ADC, ACD.
1
2
A
D
C
B
38°
102°
A
D
B
C
108°
32°
Слайд 44Теорема. Из точки, не лежащей на прямой, можно провести перпендикуляр к
этой прямой, и при том только один.
В
А
С
М
В
А
С
М
Н
1
2
Н
Н1
А
В
С
Слайд 46А
М
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Сколько
медиан может иметь треугольник?
Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.
Слайд 47А
М
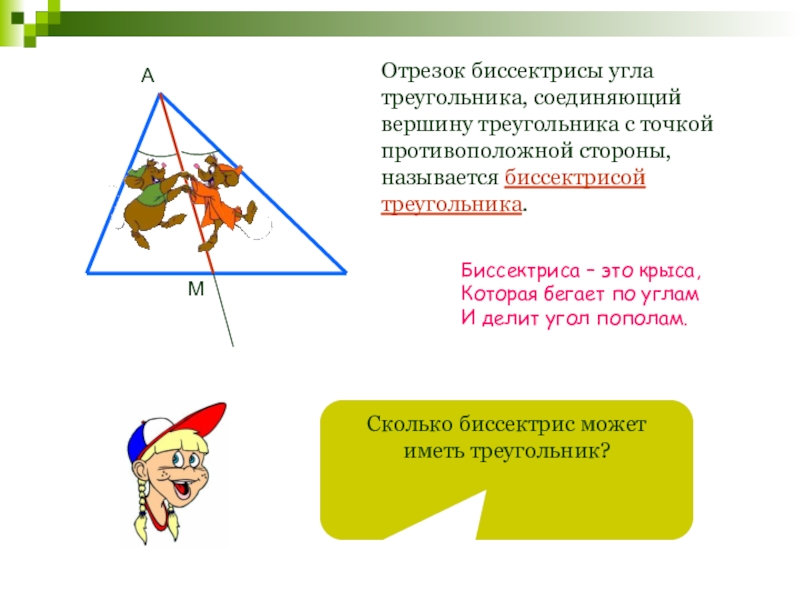
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой треугольника.
Сколько биссектрис может иметь треугольник?
Биссектриса – это крыса,
Которая бегает по углам
И делит угол пополам.
Слайд 48А
Н
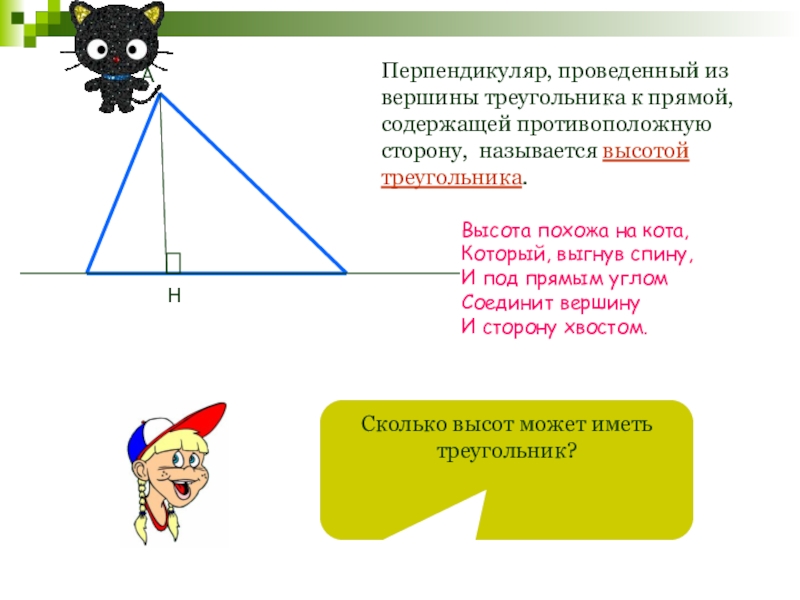
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется
высотой треугольника.
Сколько высот может иметь треугольник?
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.
Слайд 49Убедитесь на практике в том, что
в любом треугольнике медианы пересекаются
в одной точке;
в любом треугольнике биссектрисы; пересекаются в одной точке;
в любом треугольнике высоты пересекаются в одной точке.
в любом треугольнике биссектрисы; пересекаются в одной точке;
в любом треугольнике высоты пересекаются в одной точке.
Слайд 53
Подготовьте ответы на следующие вопросы:
Что называют перпендикуляром, проведенным из точки к
прямой?
Что называют основанием перпендикуляра?
Сформулируйте теорему о перпендикуляре, проведенном из точки к прямой.
Что такое медиана треугольника?
Что такое биссектриса треугольника?
Что такое высота треугольника?
Каким свойством обладают медианы, биссектрисы и высоты треугольника?
Что называют основанием перпендикуляра?
Сформулируйте теорему о перпендикуляре, проведенном из точки к прямой.
Что такое медиана треугольника?
Что такое биссектриса треугольника?
Что такое высота треугольника?
Каким свойством обладают медианы, биссектрисы и высоты треугольника?
Слайд 54
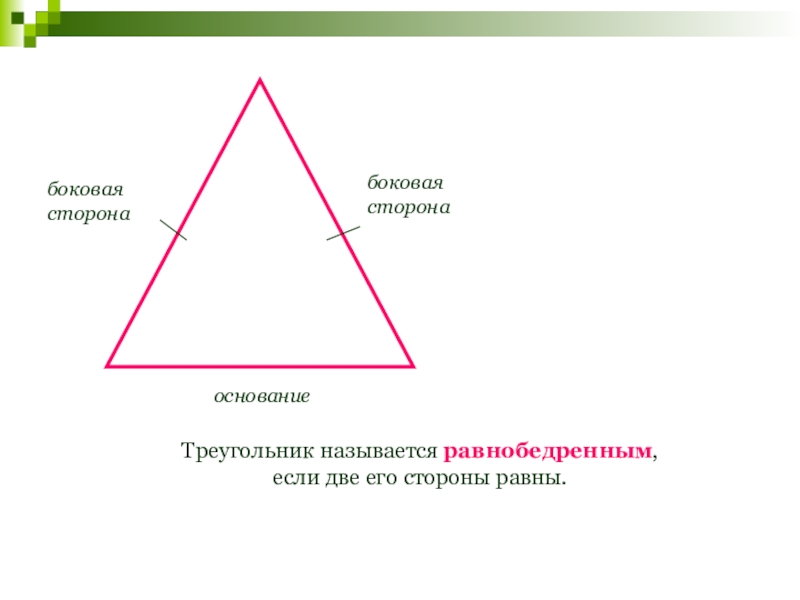
Треугольник называется равнобедренным, если две его стороны равны.
боковая сторона
боковая сторона
основание
Слайд 57Теорема.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
1
2
В
С
D
А
3
4
Слайд 58
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Высота равнобедренного
треугольника, проведенная к основанию, является медианой и биссектрисой.
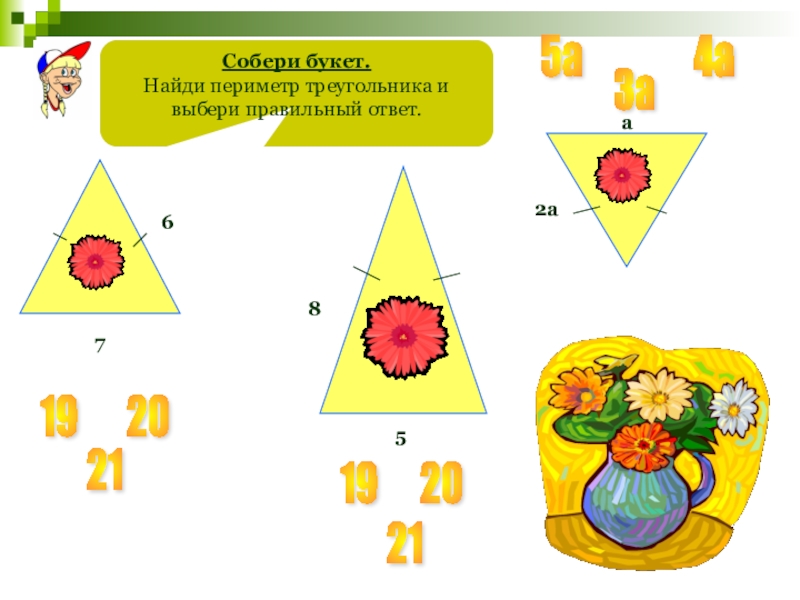
Слайд 63
6
7
19
20
21
8
5
19
20
21
2а
а
5а
4а
3а
Собери букет.
Найди
периметр треугольника и выбери правильный ответ.
Слайд 70
Подготовьте ответы на следующие вопросы:
Какой треугольник называется равнобедренным?
Как называются стороны равнобедренного
треугольника?
Какой треугольник называется равносторонним?
Какой треугольник называется равносторонним?
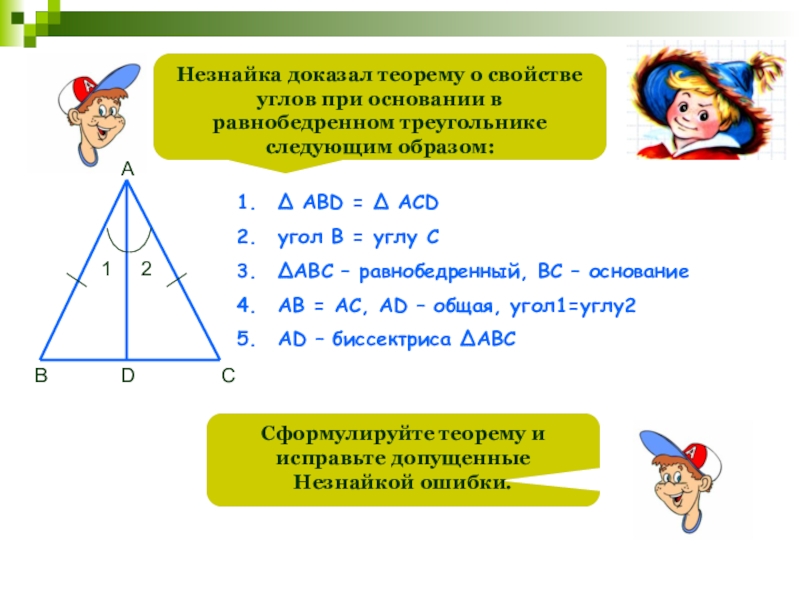
Слайд 71Незнайка доказал теорему о свойстве углов при основании в равнобедренном треугольнике
следующим образом:
∆ АВD = ∆ ACD
угол В = углу С
∆АВС – равнобедренный, ВС – основание
АВ = АС, AD – общая, угол1=углу2
AD – биссектриса ∆АВС
1
2
В
С
D
A
Сформулируйте теорему и исправьте допущенные Незнайкой ошибки.
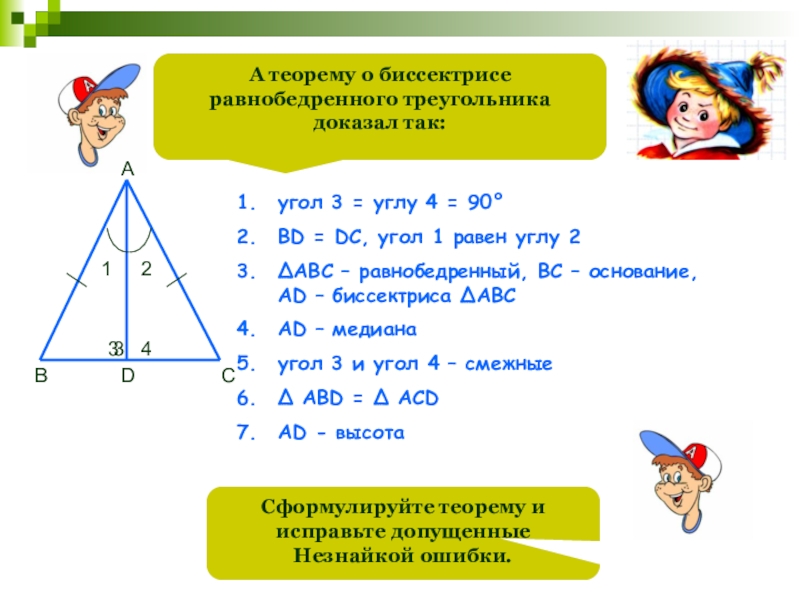
Слайд 72А теорему о биссектрисе равнобедренного треугольника доказал так:
угол 3 = углу
4 = 90°
BD = DC, угол 1 равен углу 2
∆АВС – равнобедренный, ВС – основание, AD – биссектриса ∆АВС
AD – медиана
угол 3 и угол 4 – смежные
∆ АВD = ∆ ACD
AD - высота
BD = DC, угол 1 равен углу 2
∆АВС – равнобедренный, ВС – основание, AD – биссектриса ∆АВС
AD – медиана
угол 3 и угол 4 – смежные
∆ АВD = ∆ ACD
AD - высота
1
2
В
С
D
A
Сформулируйте теорему и исправьте допущенные Незнайкой ошибки.
3
3
4
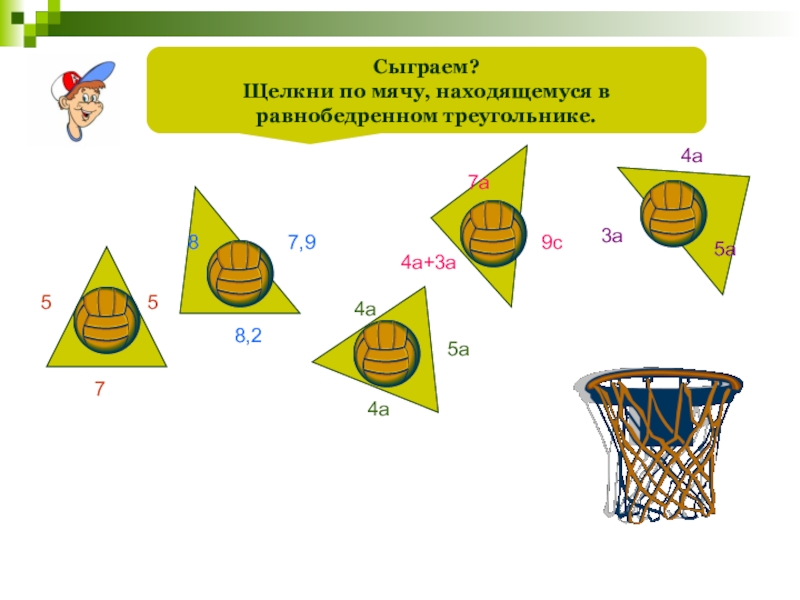
Слайд 73
Сыграем?
Щелкни по мячу, находящемуся в равнобедренном треугольнике.
5
5
7
4а
4а
5а
3а
4а
5а
8
8,2
7,9
7а
4а+3а
9с
Слайд 84Самостоятельная работа.
В равнобедренном треугольнике сумма всех углов равна 180°. Найдите углы
этого треугольника, если известно, что один них равен 38°.
В треугольнике АВС стороны АВ и ВС равны, ВМ – медиана, угол АВM равен 44°. Найдите неизвестные углы треугольника АВС.
В треугольнике АВС стороны АВ и ВС равны, ВМ – медиана, угол АВM равен 44°. Найдите неизвестные углы треугольника АВС.
В равнобедренном треугольнике сумма всех углов равна 180°. Найдите углы этого треугольника, если известно, что один них равен 62°.
В треугольнике АОС стороны АО и ОС равны, ОН – высота, угол АОН равен 32°. Найдите неизвестные углы треугольника АОС.
1 вариант
2 вариант
Слайд 87Математический диктант.
Перпендикуляр к прямой – это …
Сколько перпендикуляров можно провести из
точки не лежащей на прямой, к этой прямой?
Биссектриса треугольника – это …
Какой треугольник называют равнобедренным?
Назовите стороны равнобедренного треугольника.
Сформулируйте теорему об углах при основании в равнобедренном треугольнике.
Биссектриса треугольника – это …
Какой треугольник называют равнобедренным?
Назовите стороны равнобедренного треугольника.
Сформулируйте теорему об углах при основании в равнобедренном треугольнике.
Основание перпендикуляра – это …
Медиана треугольника- это …
Высота треугольника это - …
В любом треугольнике медианы, высоты и биссектрисы пересекаются …
Какой треугольник называют равносторонним?
Сформулируйте теорему о биссектрисе равнобедренного треугольника, проведенной к основанию.
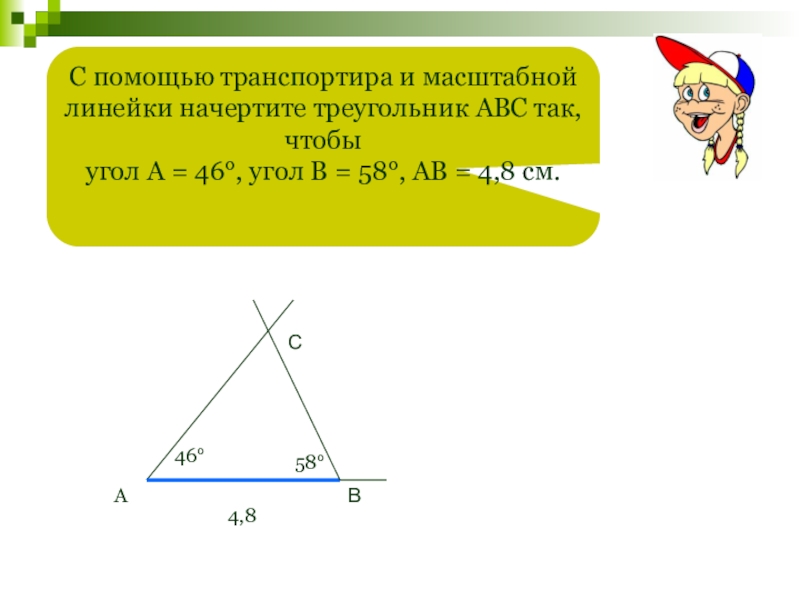
Слайд 89С помощью транспортира и масштабной линейки начертите треугольник АВС так, чтобы
угол А = 46°, угол В = 58°, АВ = 4,8 см.
А
46°
4,8
58°
В
С
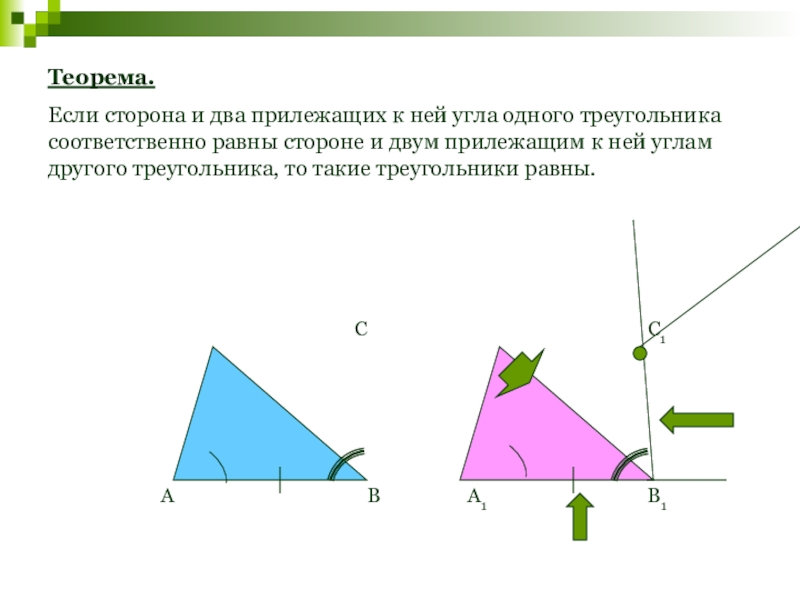
Слайд 90Теорема.
Если сторона и два прилежащих к ней угла одного треугольника соответственно
равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
А
С
В
А1
С1
В1
Слайд 101Самостоятельная работа.
Отрезки МК и ВО пересекаются в точке О. Точка О
является серединой отрезка МК, угол М = углу К. Докажите, что ∆МОВ = ∆КОА.
Докажите, что медиана, проведенная к основанию равнобедренного треугольника, разбивает его на два равных треугольника.
Докажите, что медиана, проведенная к основанию равнобедренного треугольника, разбивает его на два равных треугольника.
Отрезки AD и ВС пересекаются в точке О, АО = ОD, угол А равен углу D. Докажите, что ∆АОВ = ∆DOC.
В равнобедренном треугольнике АВС на основании АС лежат две точки О и К, причем угол АВО = углу СВК. Докажите, что треугольники АВО и СВК равны.
Слайд 104
Ребята, что в вашем понимании значит слово «понятие»?
Понятие – это слово
или словосочетание, обозначающее предмет, явление или свойства предметов, отношения между ними и т.д.
Например,
лес,
смелость,
неравенство,
треугольник.
Слайд 105
У каждого понятия есть содержание:
Содержание понятия – это свойства, ВСЕГДА присущие
тому предмету или явлению, которые обозначает понятие.
Например,
Треугольник:
геометрическая фигура;
состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Слайд 106
Для каждого понятия можно указать его объем:
Объем понятия – круг предметов,
которые обладают существенными свойствами содержания понятия.
Например,
Единичные понятия: Москва, сказка «Репка», первый признак равенства треугольников.
Общие понятия: школьный предмет, треугольники.
Пустые понятия: треугольник с двумя тупыми углами.
Слайд 107
Определите, каков объем каждого понятия:
Треугольник;
прямая, параллельная данной;
второй признак равенства
треугольников;
точка, через которую проходят четыре медианы треугольника; признак равенства треугольников;
угол, смежный с данным углом;
равнобедренный треугольник.
точка, через которую проходят четыре медианы треугольника; признак равенства треугольников;
угол, смежный с данным углом;
равнобедренный треугольник.
Слайд 109
Когда вы решаете задачу, отвечаете на вопросы учителя, вы думаете –
осуществляете умственное действие.
Умственное действие
Обобщение – обобщить понятие – значит показать к какой группе понятий принадлежит данное понятие.
Волга – река.
Равнобедренный треугольник – треугольник.
Медиана – отрезок.
Конкретизация – приведение конкретных примеров понятия.
Газета – «Аргументы и факты»
Треугольник – прямоугольный треугольник.
Угол – острый угол.
Слайд 110
А теперь мы узнаем, что такое определение:
Определение понятия – раскрытие его
содержания, то есть перечисление всех существенных признаков понятия, необходимых для его распознавания.
Определение понятия соединяет обобщение и конкретизацию.
Определение понятия соединяет обобщение и конкретизацию.
Обобщение, которое приводится в определении понятий, называется родовым признаком.
Например,
Медиана, высота, биссектриса треугольника – отрезки.
Слайд 111
Познакомимся с рядом определений:
Окружностью называется геометрическая фигура, состоящая из всех точек,
расположенных на заданном расстоянии от данной точки.
Данная точка называется центром окружности.
О
Слайд 115
О
А
В
Любые две точки окружности делят ее на две части. Каждая
из этих частей называется дугой окружности.
М
К
Слайд 127
Ответьте на следующие вопросы:
Что такое определение понятия?
Дайте определение окружности.
Что такое центр
окружности?
Что такое радиус?
Что такое хорда?
Что называется диаметром?
Что называется дугой окружности?
С помощью какого инструмента можно построить окружность?
Что называется кругом?
Что такое радиус?
Что такое хорда?
Что называется диаметром?
Что называется дугой окружности?
С помощью какого инструмента можно построить окружность?
Что называется кругом?
Слайд 128Самостоятельная работа.
1 вариант
Отрезки КМ и EF являются диаметрами окружности с центром
в точке О.
Докажите, что:
угол FEM равен углу КМЕ;
отрезки КЕ и MF равны.
Докажите, что:
угол FEM равен углу КМЕ;
отрезки КЕ и MF равны.
2 вариант
Отрезки МЕ и РК являются диаметрами окружности с центром О.
Докажите, что:
угол ЕМР равен углу МРК;
отрезки МК и РЕ равны.
Слайд 133Задача. Дана прямая и точка на ней. Построить прямую, проходящую через данную
точку и перпендикулярную к данной прямой.
а
а
А
В
Р
Q
M
а
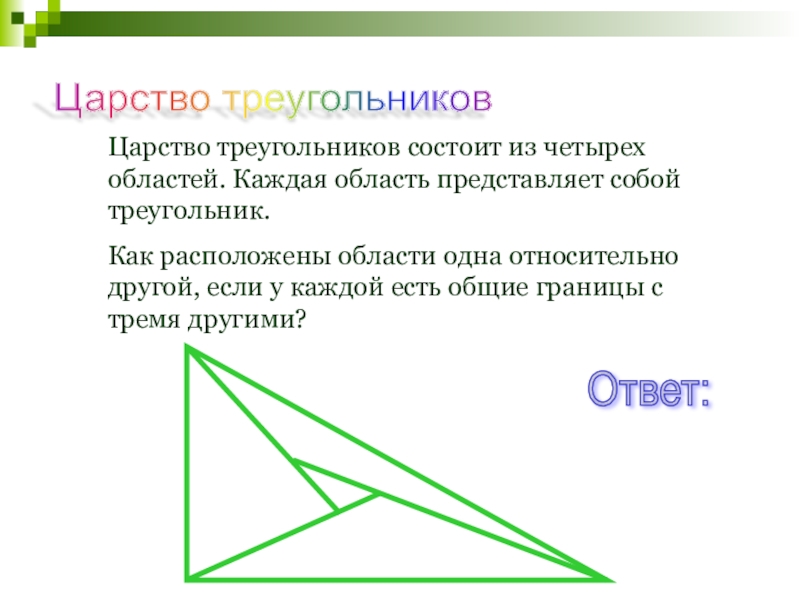
Слайд 138Царство треугольников
Царство треугольников состоит из четырех областей. Каждая область представляет
собой треугольник.
Как расположены области одна относительно другой, если у каждой есть общие границы с тремя другими?
Как расположены области одна относительно другой, если у каждой есть общие границы с тремя другими?
Ответ:
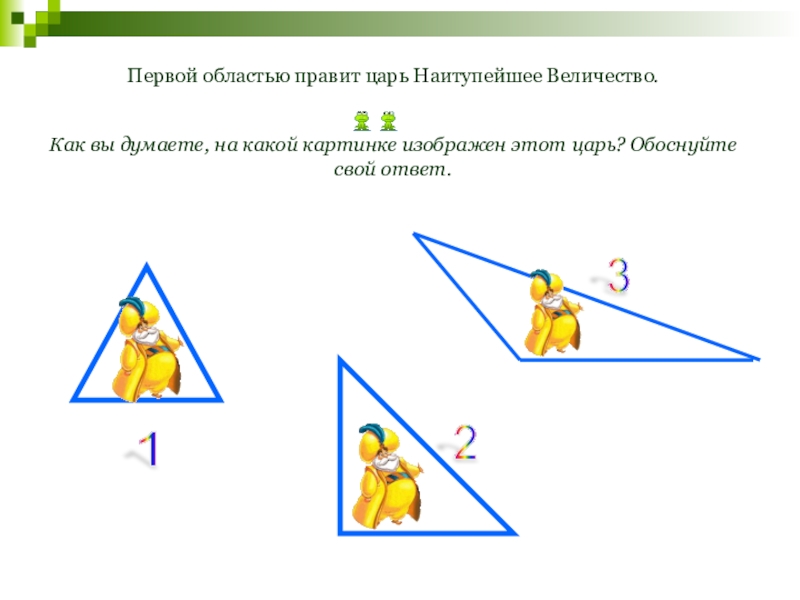
Слайд 139Первой областью правит царь Наитупейшее Величество.
Как вы думаете, на какой картинке
изображен этот царь? Обоснуйте свой ответ.
1
2
3
Слайд 140Второй областью правит царица Высота.
Дайте определение высоты треугольника.
Начертите в тетради тупоугольный
треугольник и постройте его высоты.
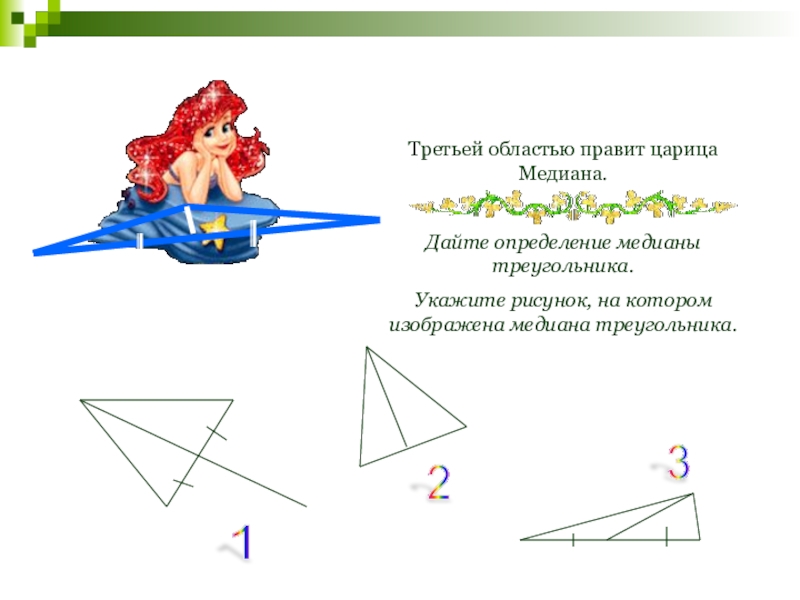
Слайд 141Третьей областью правит царица Медиана.
Дайте определение медианы треугольника.
Укажите рисунок, на
котором изображена медиана треугольника.
1
2
3
Слайд 142Четвертой областью правит царица Биссектриса.
Дайте определение биссектрисы треугольника.
Постройте треугольник АВС
такой, чтобы угол А был равен 120°. Постройте биссектрису угла А, с помощью циркуля и линейки.
Слайд 143В царстве Треугольников был издан Свод законов, в котором были записаны
основные определения и теоремы, и которым все жители царства неукоснительно следовали.
Какие, на ваш взгляд, утверждения не должны быть записаны в Своде законов (щелкните по ним, и они исчезнут)?
Какие, на ваш взгляд, утверждения не должны быть записаны в Своде законов (щелкните по ним, и они исчезнут)?
В равнобедренном треугольнике медианы равны.
Если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны.
В равнобедренном треугольнике любая медиана делит треугольник на два равных треугольника.
Высота любого треугольника проходит во внутренней его области.
В равностороннем треугольнике все медианы, высоты и биссектрисы пересекаются в одной точке.
Слайд 145
Продолжите фразы:
Треугольником называется …
Треугольник обозначается …
Высотой треугольника называется …
Медианой треугольника называется
…
Биссектрисой треугольника называется …
Перпендикулярность прямых а и b обозначается …
Треугольник называется равносторонним …
Основанием равнобедренного треугольника …
Треугольник называется равносторонним …
В равнобедренном треугольнике биссектриса, проведенная к основанию, …
Биссектрисой треугольника называется …
Перпендикулярность прямых а и b обозначается …
Треугольник называется равносторонним …
Основанием равнобедренного треугольника …
Треугольник называется равносторонним …
В равнобедренном треугольнике биссектриса, проведенная к основанию, …
Слайд 146
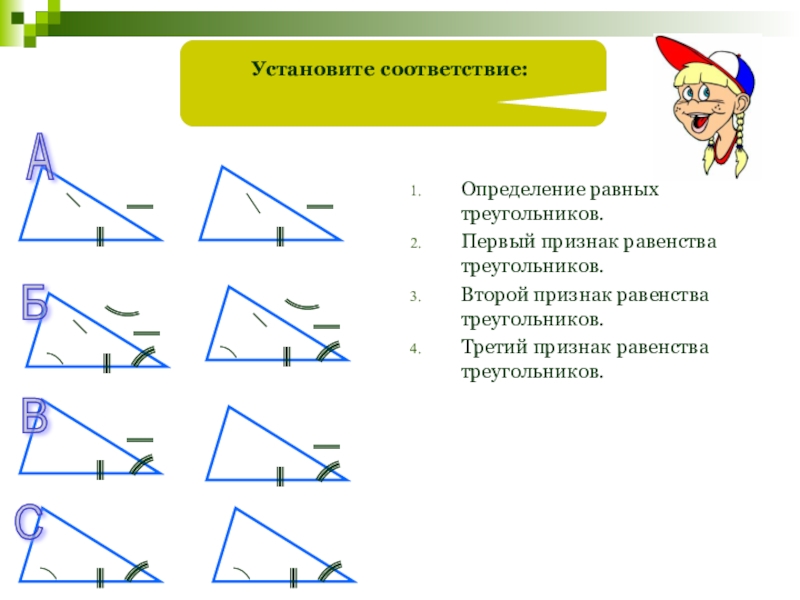
Установите соответствие:
Определение равных треугольников.
Первый признак равенства треугольников.
Второй признак равенства треугольников.
Третий признак
равенства треугольников.
А
Б
В
С
Слайд 147
В следующем задании щелкните по правильным ответам, и вы увидите картинку.
Решение
задач оформите в тетради.
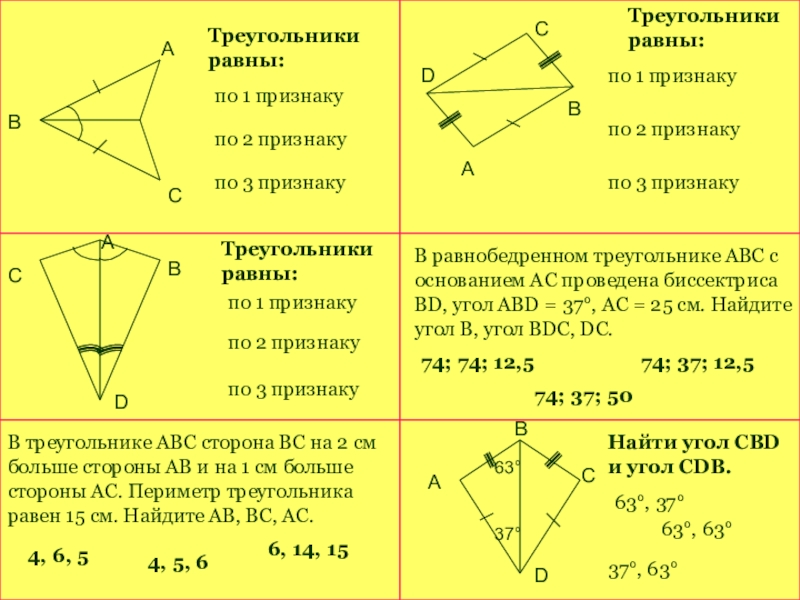
Слайд 148
А
В
С
Треугольники равны:
по 1 признаку
по 2 признаку
по 3 признаку
Треугольники равны:
по 1 признаку
по
2 признаку
по 3 признаку
А
В
С
D
Треугольники равны:
по 1 признаку
по 2 признаку
по 3 признаку
A
D
B
C
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса BD, угол АВD = 37°, АС = 25 см. Найдите угол В, угол ВDС, DC.
74; 74; 12,5
74; 37; 12,5
74; 37; 50
В треугольнике АВС сторона ВС на 2 см больше стороны АВ и на 1 см больше стороны АС. Периметр треугольника равен 15 см. Найдите АВ, ВС, АС.
4, 6, 5
4, 5, 6
6, 14, 15
63°
37°
А
В
С
D
Найти угол CBD и угол CDB.
63°, 37°
37°, 63°
63°, 63°
