- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Решение задач Центральные и вписанные углы
Содержание
- 1. Презентация по теме Решение задач Центральные и вписанные углы
- 2. Задание№1Центральный угол AOB опирается на хорду AB
- 3. В окружности с центром в точке O
- 4. Найдите угол DEF, если градусная мера дуг
- 5. Прямоугольный треугольник с катетами 5см и 12см
- 6. Точки A и B делят окружность на две дуги, длины которых
- 7. решение: угол ACB — вписанный, он равен половине дуги AB.
- 8. Точка O – центр окружности, на которой лежат точки A,
- 9. Литература. Открытый банк заданий ОГЭ. Математика2016http://85.142.162.126/os/xmodules/qprint/index.php?proj=DE0E276E497AB3784C3FC4CC20248DC0
Слайд 1 Решение задач на тему: центральные и вписанные углы Выполнила учитель математики Гридасова
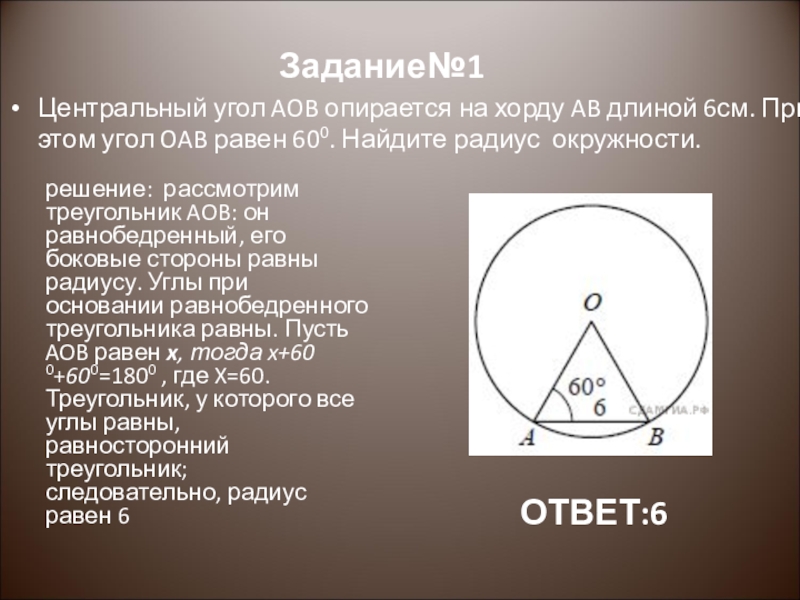
Слайд 2Задание№1
Центральный угол AOB опирается на хорду AB длиной 6см. При этом
решение: рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу. Углы при основании равнобедренного треугольника равны. Пусть AOB равен x, тогда x+60 0+600=1800 , где X=60. Треугольник, у которого все углы равны, равносторонний треугольник; следовательно, радиус равен 6
ОТВЕТ:6
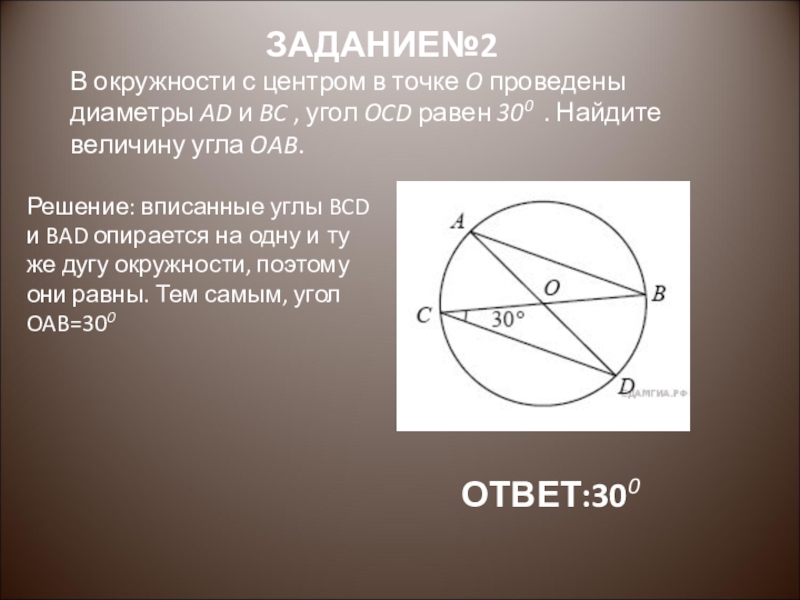
Слайд 3В окружности с центром в точке O проведены диаметры AD и
ЗАДАНИЕ№2
ОТВЕТ:300
Решение: вписанные углы BCD и BAD опирается на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол OAB=300
Слайд 4Найдите угол DEF, если градусная мера дуг DE и EF равны
Решение: дуга FD, не содержащая точку E, равна 3600-1500-680=1420, поэтому угол DEF=1420
ЗАДАНИЕ№3
ОТВЕТ: 710
Решение: дуга FD, не содержащая точку E, равна 3600-1500-680=1420, угол DEF вписанный, поэтому угол DEF=142:2=710
Слайд 5Прямоугольный треугольник с катетами 5см и 12см вписан в окружность. Чему
ЗАДАНИЕ№4
ОТВЕТ:6,5
РЕШЕНИЕ: ПУСТЬ R- РАДИУС ОПИСАННОЙ ОКРУЖНОСТИ. ТАК КАК ОКРУЖНОСТЬ ОПИСАНА ВОКРУГ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА, ТО ЕЕ ЦЕНТР ЛЕЖИТ НА СЕРЕДИНЕ ГИПОТЕНУЗЫ . ТАКИМ ОБРАЗОМ, ГИПОТЕНУЗА РАВНА 2R.
ПО ТЕОРЕМЕ ПИФАГОРА ИМЕЕМ:
Слайд 6Точки A и B делят окружность на две дуги, длины которых относятся как 9:11. Найдите
ЗАДАНИЕ№5
Дуги окружности относятся как 9:11, что в сумме дает 20 частей. Поэтому длина меньшей дуги составляет  от всей окружности, тем самым, она равна . Угол AOB=162:2=81
ОТВЕТ:162
Так как угол AOB-центральный, то он равен той дуге на которую он опирается. Таким образом, 
Слайд 7решение: угол ACB — вписанный, он равен половине дуги AB. Угол АОВ — центральный, опирающийся на
В угол величиной 70° вписана окружность, которая касается его сторон в точках A и B. На одной из дуг этой окружности выбрали точку C так, как показано на рисунке. Найдите величину угла ACB.
ОТВЕТ:55
ЗАДАНИЕ№6
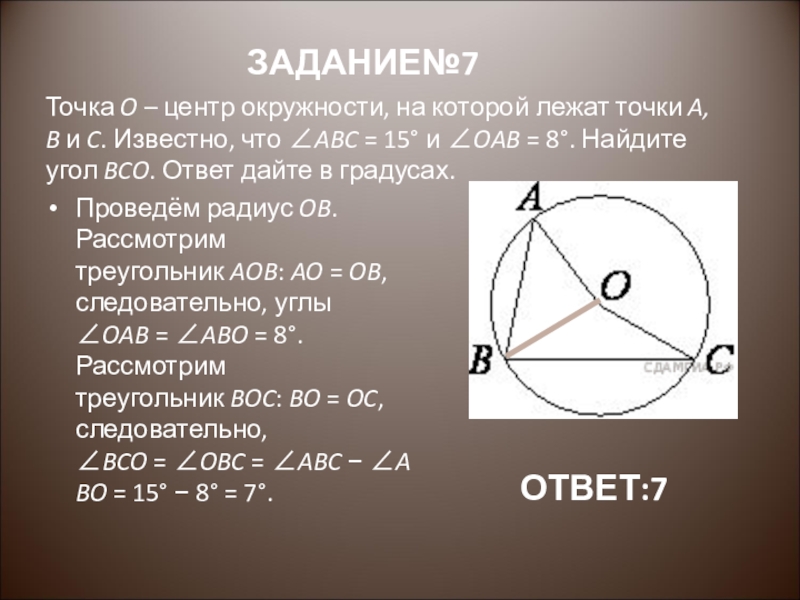
Слайд 8Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 15°
Проведём радиус OB. Рассмотрим треугольник AOB: AO = OB, следовательно, углы ∠OAB = ∠ABO = 8°. Рассмотрим треугольник BOC: BO = OC, следовательно, ∠BCO = ∠OBC = ∠ABC − ∠ABO = 15° − 8° = 7°.
ОТВЕТ:7
ЗАДАНИЕ№7