- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: простейшие задачи в координатах
Содержание
- 1. Презентация по теме: простейшие задачи в координатах
- 2. СодержаниеРадиус-вектор Связь между координатами вектора и координатами
- 3. Связь между координатами вектора и координатами его начала и конца.
- 4. Согласны ли вы с утверждениемКоординаты вектора – это коэффициенты разложения вектора по коллинеарным векторам.координатным
- 5. ????????
- 6. Согласны ли вы с утверждениемверноКаждая координата суммы двух векторов равна сумме соответствующих координат этих векторов.
- 7. Найти координаты векторов.
- 8. М(х0; у0)х0у0ухРадиус вектор
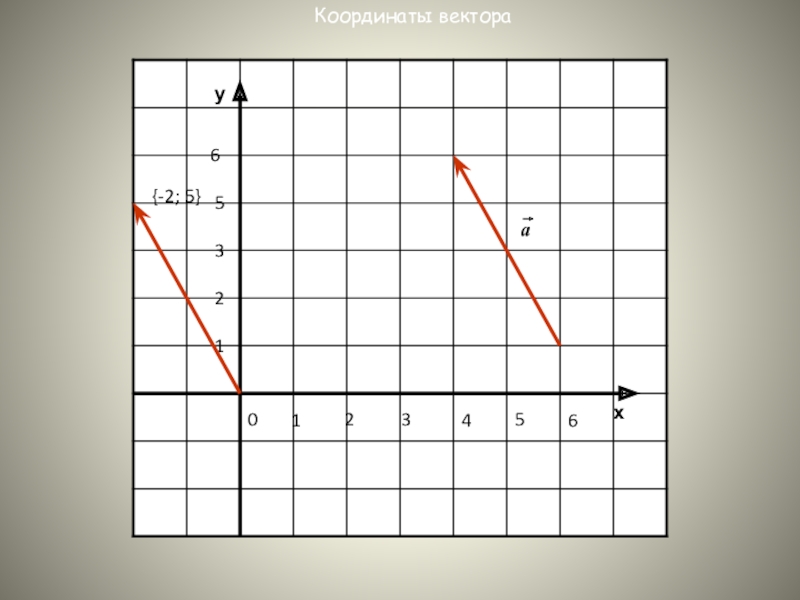
- 9. ху153201543266Координаты вектора{-2; 5}a
- 10. ху153201543266Координаты вектораВ(х2; у2)А(х1; у1)АВ=ОВ-ОА
- 11. Каждая координата вектора равна разности соответствующих координат
- 12. { } {-4;
- 13. Слайд 13
- 14. Координаты середины отрезка
- 15. C (x0;y0)A(x1;y1)B(x2;y2)xyОКоординаты середины отрезка
- 16. Найдите координаты cередин отрезковR(2;7); M(-2;7);
- 17. Длина вектора
- 18. ==xyОВычисление длины вектора по его координатамOA2=OA12 + AA12xyOA2= x2 + y2
- 19. Расстояние между точками
- 20. Расстояние между двумя точками M2(x2;y2)M1(x1;y1)d
- 21. Слайд 21
- 22. 1 вариант2 вариантПроверка теста
- 23. Критерии оценок«5» - нет ошибок«4» - одна ошибка«3» - две ошибки
- 24. Домашнее задание1. п. 88, 89, выучить формулы2. № 935 , № 936 , 938
- 25. Оцени свою работу на урокеУрок 1. интересно2. скучно 3.безразлично
- 26. Спасибо за работу
- 27. xyOACB533 ABCО – прямоугольная трапеция. Найдите
- 28. xyOACB824 ABCО – прямоугольная трапеция. Найдите
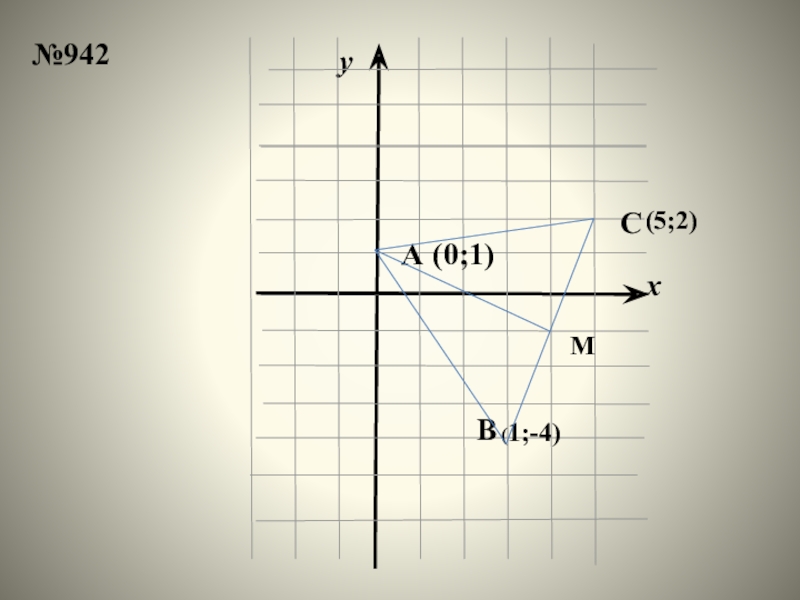
- 29. xyA(0;1)(1;-4)ВС(5;2)М№942
- 30. xyO108 На рисунке ОВ=10, ОА=
СодержаниеРадиус-вектор Связь между координатами вектора и координатами его начала и конца Координаты середины отрезкаВычисление длины вектора по его координатамРасстояние между двумя точками
Слайд 2Содержание
Радиус-вектор
Связь между координатами вектора и координатами его начала и конца
Координаты середины отрезка
Вычисление длины вектора по его координатам
Расстояние между двумя точками
Слайд 4Согласны ли вы с утверждением
Координаты вектора – это коэффициенты разложения вектора
по коллинеарным векторам.
координатным
Слайд 6Согласны ли вы с утверждением
верно
Каждая координата суммы двух векторов равна сумме
соответствующих координат этих векторов.
Слайд 11Каждая координата вектора равна разности соответствующих координат его конца и начала
Даны
точки А(х1; у1) и В(х2; у2), тогда
Координаты вектора АВ{х2 – х1; у2 – у1}
Координаты вектора АВ{х2 – х1; у2 – у1}
Слайд 12{ } {-4; 0}
Найти координаты векторов.
{ } {0; 6}
{ } { 3; 5}
{ } {-4; -3}
{ } {5; -14}
{ } {0; -7}
Слайд 16Найдите координаты
cередин отрезков
R(2;7); M(-2;7); C
P(-5;1); D(-5;7);
C
R(-3;0); N(0;5); C
A(0;-6); B(-4;2); C
R(-7;4); T(-2;-7); C
A(7;7); B(-2;0); C
( ; );
2
2+(-2)
2
7 + 7
C(0; 7)
C(-5; 4)
C(-1,5; 2,5)
C(-2;-2)
C(2,5; 3,5)
C(-4,5;-1,5)
Слайд 25Оцени свою работу на уроке
Урок
1. интересно
2. скучно
3.безразлично
Итог
1. понял материал
2.
узнал больше, чем знал
3. не понял
3. не понял
Я на уроке
1. работал
2. отдыхал
3.помогал другим
Слайд 27x
y
O
A
C
B
5
3
3
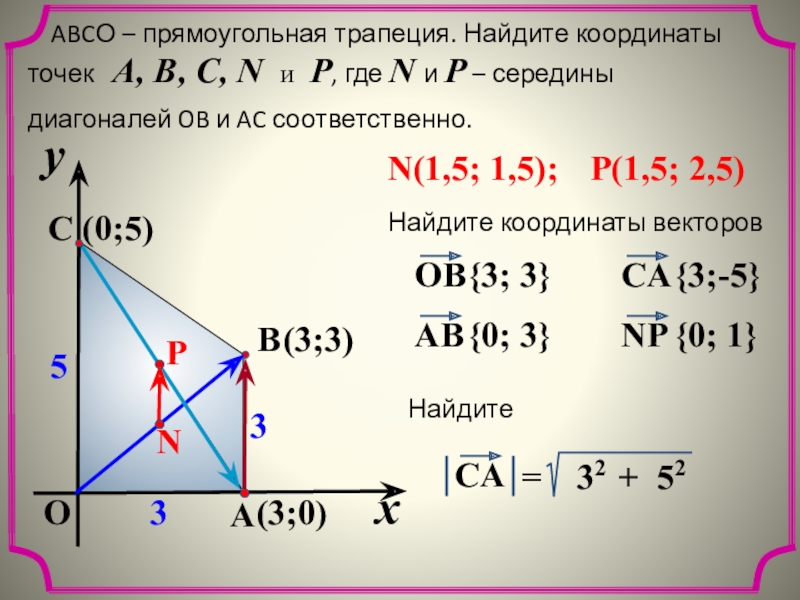
ABCО – прямоугольная трапеция. Найдите координаты точек A,
B, C, N и P, где N и P – середины
диагоналей OB и AC соответственно.
диагоналей OB и AC соответственно.
(3;3)
(0;5)
N(1,5; 1,5);
P(1,5; 2,5)
(3;0)
{3; 3}
{0; 3}
{3;-5}
{0; 1}
Слайд 28x
y
O
A
C
B
8
2
4
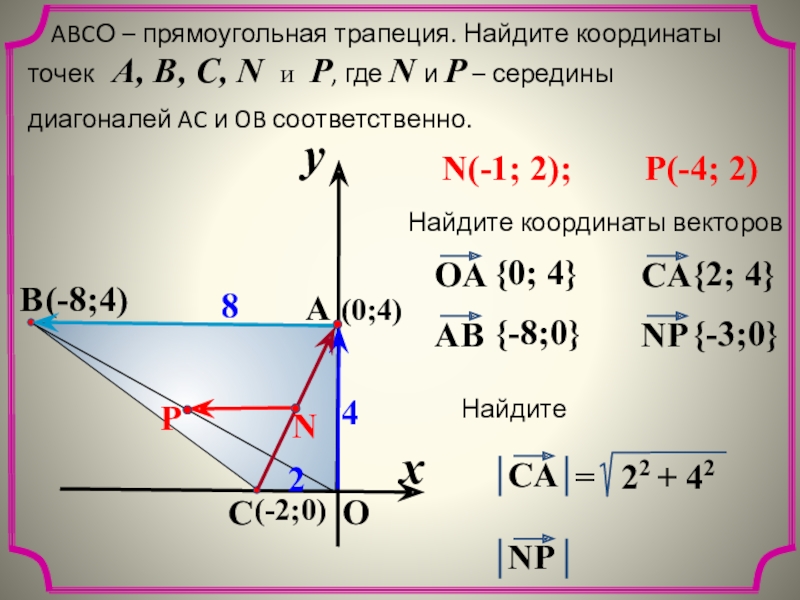
ABCО – прямоугольная трапеция. Найдите координаты точек A,
B, C, N и P, где N и P – середины
диагоналей AC и OB соответственно.
диагоналей AC и OB соответственно.
(-8;4)
(-2;0)
N(-1; 2);
P(-4; 2)
(0;4)
{0; 4}
{-8;0}
{2; 4}
{-3;0}
Слайд 30x
y
O
10
8
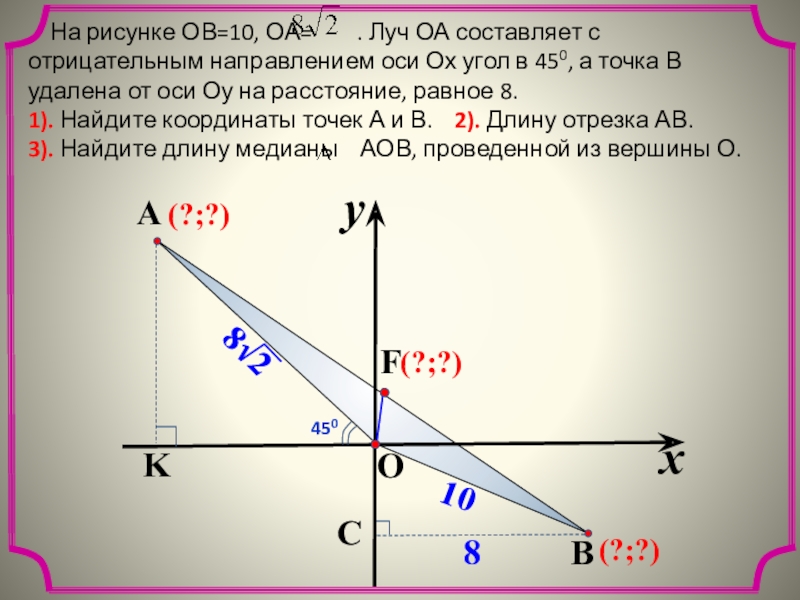
На рисунке ОВ=10, ОА= . Луч
ОА составляет с отрицательным направлением оси Ох угол в 450, а точка В удалена от оси Оу на расстояние, равное 8.
1). Найдите координаты точек А и В. 2). Длину отрезка АВ.
3). Найдите длину медианы АОВ, проведенной из вершины О.
1). Найдите координаты точек А и В. 2). Длину отрезка АВ.
3). Найдите длину медианы АОВ, проведенной из вершины О.
450
A
B
(?;?)
(?;?)
(?;?)
