- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Объем шара
Содержание
Теорема
Слайд 3
Теорема
Дано:
R — радиус шара
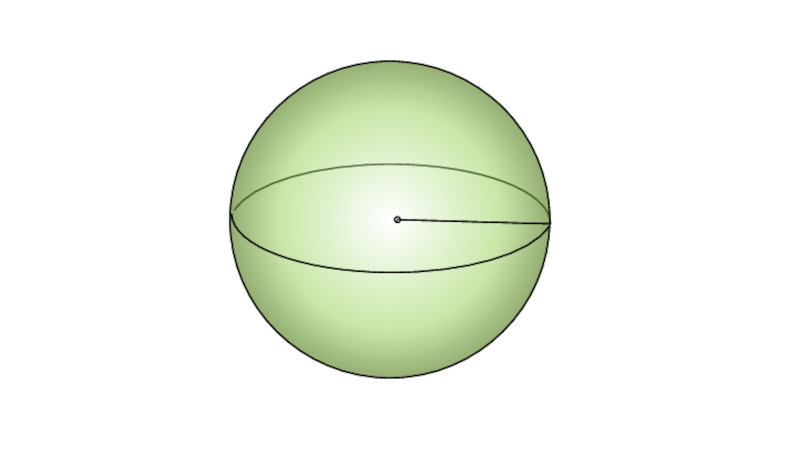
шар
1) Проведём ось OX через центр шара
Доказательство:
OP =
x, PQ = r, OQ = R
S = πR2 ⇒ S(x) = π(R2 — x2)
Теорема доказана
2) Проведём сечение через P ∈ OX и ⏊ к оси OX
3) Найдём зависимость площади сечения S от значения x
X
P
r
Q
R
x
O
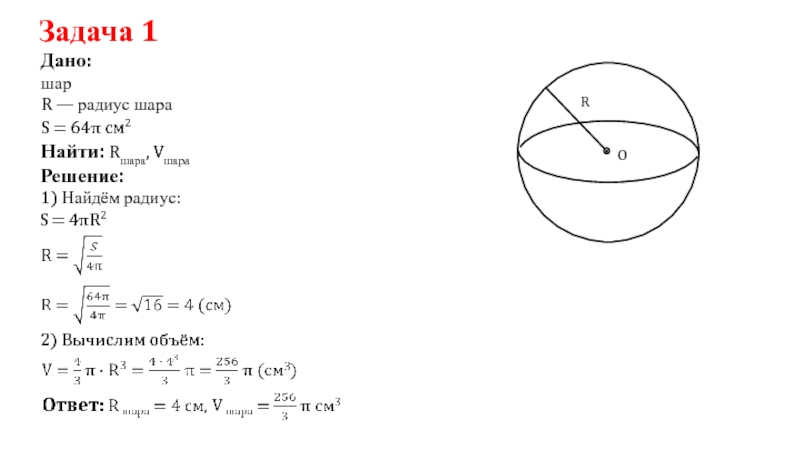
Слайд 4Задача 1
Дано:
Решение:
Найти: Rшара, Vшара
шар
1) Найдём радиус:
2) Вычислим объём:
S = 4πR2
R —
радиус шара
S = 64π см2
R
O
Слайд 5
X
O1
r1
M
r2
O2
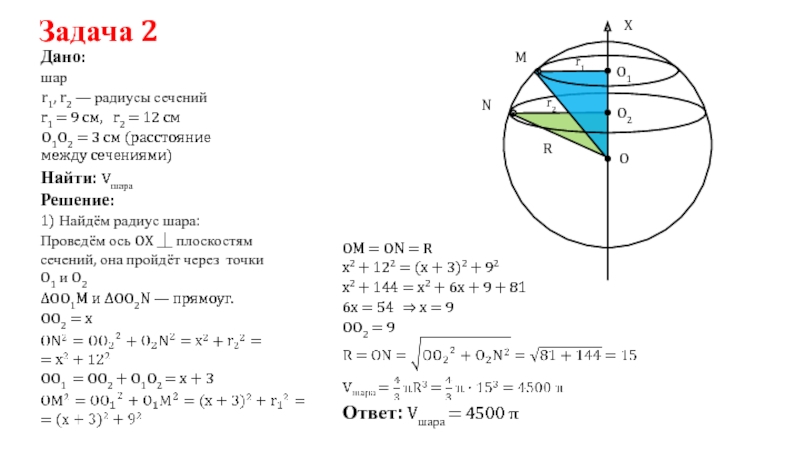
Задача 2
Дано:
Решение:
Найти: Vшара
шар
∆OO1M и ∆OO2N — прямоуг.
Ответ: Vшара = 4500
π
1) Найдём радиус шара:
OO2 = x
Проведём ось OX ⏊ плоскостям сечений, она пройдёт через точки O1 и O2
r1, r2 — радиусы сечений
r1 = 9 см,
OM = ON = R
x2 + 122 = (x + 3)2 + 92
x2 + 144 = x2 + 6x + 9 + 81
6x = 54
OO2 = 9
r2 = 12 см
O1O2 = 3 см (расстояние между сечениями)
OO1 = OO2 + O1O2 = x + 3
⇒ x = 9
N
O
R
