- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Мир правильных многогранников
Содержание
- 1. Презентация по теме: Мир правильных многогранников
- 2. Мир правильных многогранников.
- 3. Математика владеет не только истиной, но и
- 4. Мир многогранниковМногогранники окружают нас в повседневной жизни
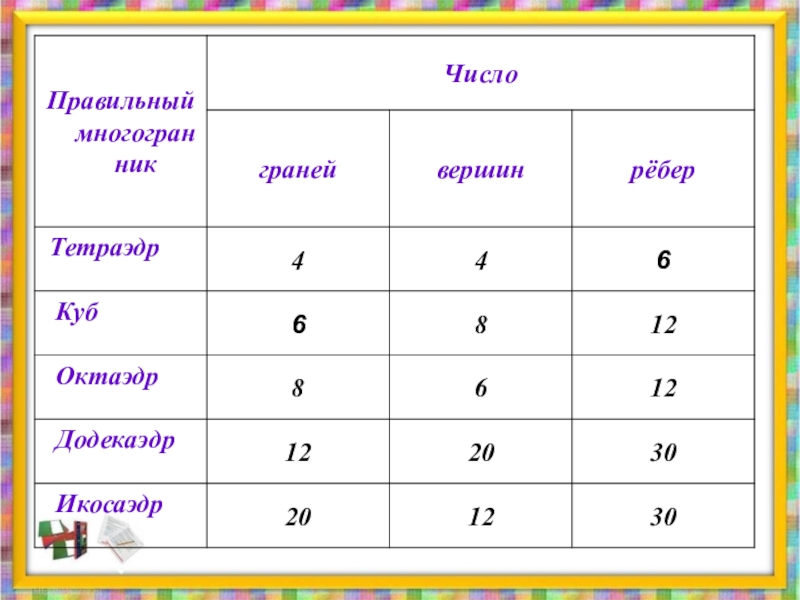
- 5. многогранникправильныйграни- равные правильные многоугольники,в каждой вершине сходится одно и то же число ребер.
- 6. «эдра» - грань «тетра» - 4 «гекса»
- 7. Тетраэдр – представитель правильных выпуклых многогранников.Поверхность тетраэдра
- 8. Куб или гексаэдр – представитель правильных выпуклых
- 9. Октаэдр – представитель семейства правильных выпуклых многогранников.Октаэдр
- 10. Додекаэдр – представительсемейства правильных выпуклых многогранников.Додекаэдр имеет
- 11. Икосаэдр – представитель семейства правильных выпуклых многогранников.Поверхность
- 12. Выпуклые правильные многогранники принято называть Платоновы
- 13. Вывод:Существует лишь пять выпуклых правильных многогранников
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
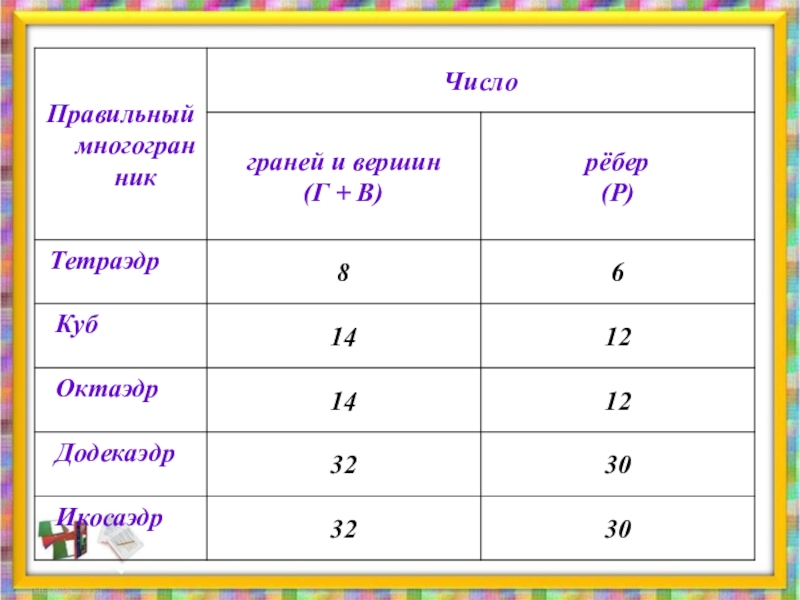
- 18. Теорема Эйлера Число вершин плюс
- 19. Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик
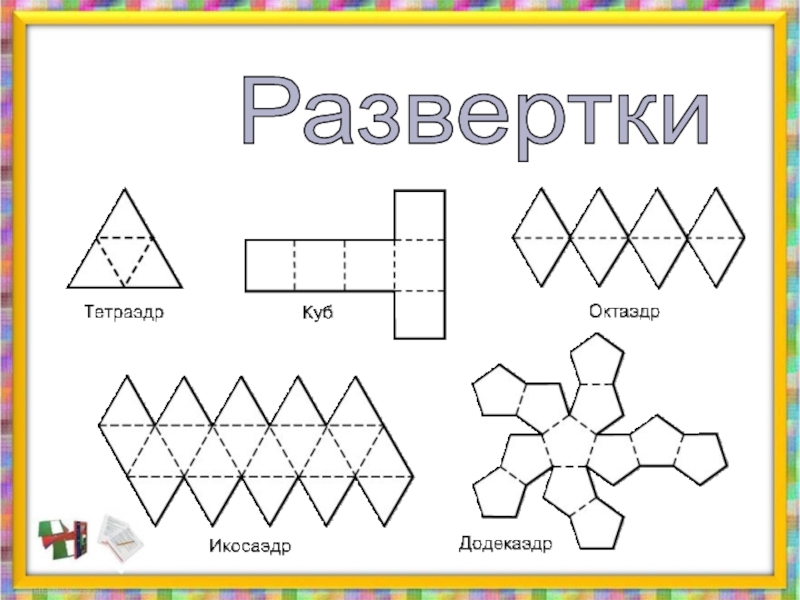
- 20. Развертки
- 21. Развертки
- 22. огоньводавоздухземлявселеннаятетраэдрикосаэдроктаэдр гексаэдрдодекаэдр
- 23. Модель Солнечной системы Кеплера.
- 24. "Космический кубок" И.Кеплера
- 25. Икосаидро-додекаидровая структура Земли.
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Симметрия многогранников в биологии.Пчёлы - удивительные создания.
- 36. Феодария Скелет одноклеточного организма феодарии (Circogonia icosahedra)
- 37. Слайд 37
- 38. Правильных многогранников вызывающе мало, но этот весьма
Мир правильных многогранников.
Слайд 3Математика владеет не только истиной, но и высшей красотой - красотой
отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.
Бертран Рассел
Бертран Рассел
Слайд 4Мир многогранников
Многогранники окружают нас в
повседневной жизни ежедневно:
спичечный коробок,
книга,
комната, гайки, башни Кремля, знаменитые Египетские пирамиды, кристаллы минералов,
различные архитектурные сооружения.
различные архитектурные сооружения.
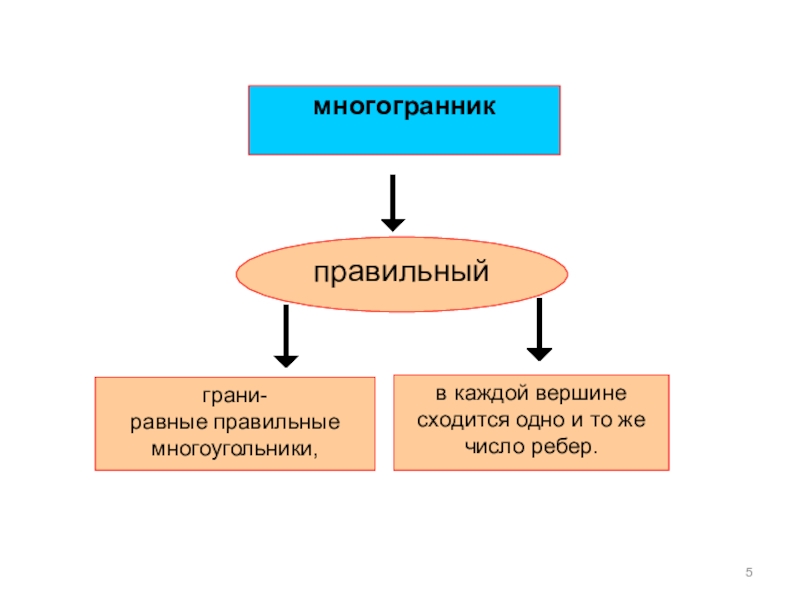
Слайд 5многогранник
правильный
грани-
равные правильные
многоугольники,
в каждой вершине сходится одно и то же
число ребер.
Слайд 7Тетраэдр – представитель правильных выпуклых многогранников.
Поверхность тетраэдра состоит из четырех равносторонних
треугольников, сходящихся в каждой вершине по три.
ТЕТРАЭДР
Слайд 8Куб или гексаэдр – представитель правильных выпуклых многогранников.
Куб имеет шесть квадратных
граней, сходящихся в каждой вершине по три.
КУБ (ГЕКСАЭДР)
Слайд 9Октаэдр – представитель семейства правильных выпуклых многогранников.
Октаэдр имеет восемь треугольных граней,
сходящихся в каждой вершине по четыре.
ОКТАЭДР
Слайд 10Додекаэдр – представитель
семейства правильных выпуклых многогранников.
Додекаэдр имеет двенадцать пятиугольных граней, сходящихся
в вершинах по три.
ДОДЕКАЭДР
Слайд 11Икосаэдр – представитель семейства правильных выпуклых многогранников.
Поверхность икосаэдра состоит из двадцати
равносторонних треугольников, сходящихся в каждой вершине по пять.
ИКОСАЭДР
Слайд 12
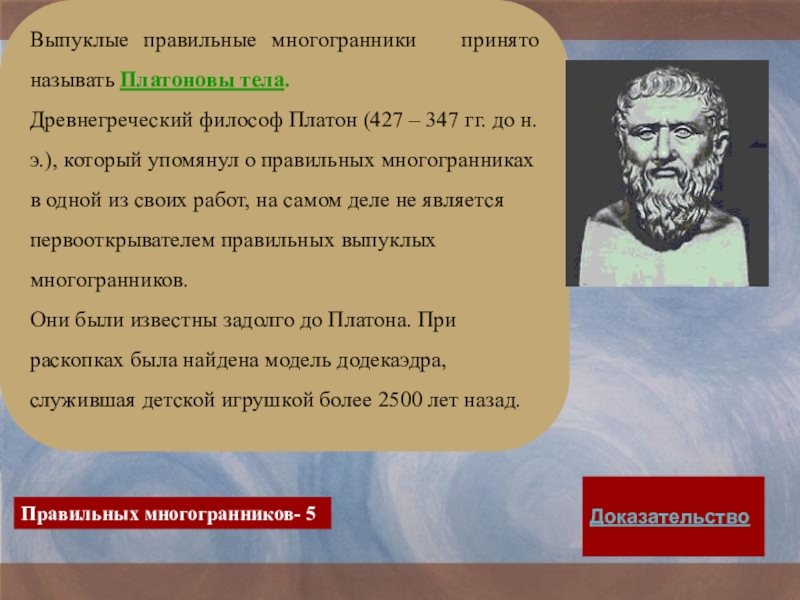
Выпуклые правильные многогранники принято называть Платоновы тела.
Древнегреческий философ Платон
(427 – 347 гг. до н.э.), который упомянул о правильных многогранниках в одной из своих работ, на самом деле не является первооткрывателем правильных выпуклых многогранников.
Они были известны задолго до Платона. При раскопках была найдена модель додекаэдра, служившая детской игрушкой более 2500 лет назад.
Они были известны задолго до Платона. При раскопках была найдена модель додекаэдра, служившая детской игрушкой более 2500 лет назад.
Доказательство
Правильных многогранников- 5
Слайд 13 Вывод:
Существует лишь пять выпуклых правильных многогранников –
тетраэдр, октаэдр
и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями
Слайд 35Симметрия многогранников в биологии.
Пчёлы - удивительные создания.
Пчелиные соты представляют собой
пространственный паркет и заполняют пространство так, что не остается просветов.
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».
Слайд 36Феодария Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство
феодарии живут на морской глубине и служат добычей коралловых рыбок. Чем же вызвана такая природная геометризация феодарии ?! Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наименьший объем при наибольшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Слайд 38Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных наук.
Л. Кэррол
Л. Кэррол