МБОУ СОШ №1 с. Кизляр, Магометова Х. Н.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора Решение заданий №9 и №11 по материалам открытого банка задач ОГЭ по математике 2016 года
Содержание
- 1. Презентация по математике на тему Теорема Пифагора Решение заданий №9 и №11 по материалам открытого банка задач ОГЭ по математике 2016 года
- 2. Теорема Пифагораc 2 = a 2 +
- 3. Задача №1Дано: ∆АВС – п/уАВ = 40,
- 4. Дано: ∆АВС – р/бАВ = 192, АС
- 5. Дано: ∆АВС – п/уАВ = 92, А
- 6. Дано: ∆АВС – р/бР∆АВС = 338, АС
- 7. Дано: ∆АВС – р/бР∆АВС = 288, АВ
- 8. Найти: Р∆ABCРешение:Задача №6
- 9. Найти: Р∆ABCРешение: (продолжение)Ответ: 78.Задача №6
- 10. Найти: ВМ.Решение: Ответ: 24.Задача №7В треугольнике АВС
- 11. Задача №8Дано: АВСD – квадратАС = 46.Найти: SABCDНайдите площадь квадрата, если его диагональ равна 46.Решение:Ответ: 1058.
- 12. Задача №9Дано: АВСD – р/б трапеция АВ
- 13. Задача №10Дано: АВСD – прямоугольник ВС =
- 14. Задача №11Дано: АВСD – ромб АВ =
- 15. Задача №12Дано: АВСD – ромб, ВН –
- 16. Задача №13Дано: АВСD – ромб, ВН –
Теорема Пифагораc 2 = a 2 + b 2cb В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. a
Слайд 1 Теорема Пифагора Решение заданий №9 и №11 по материалам открытого банка задач ОГЭ
по математике 2016 года
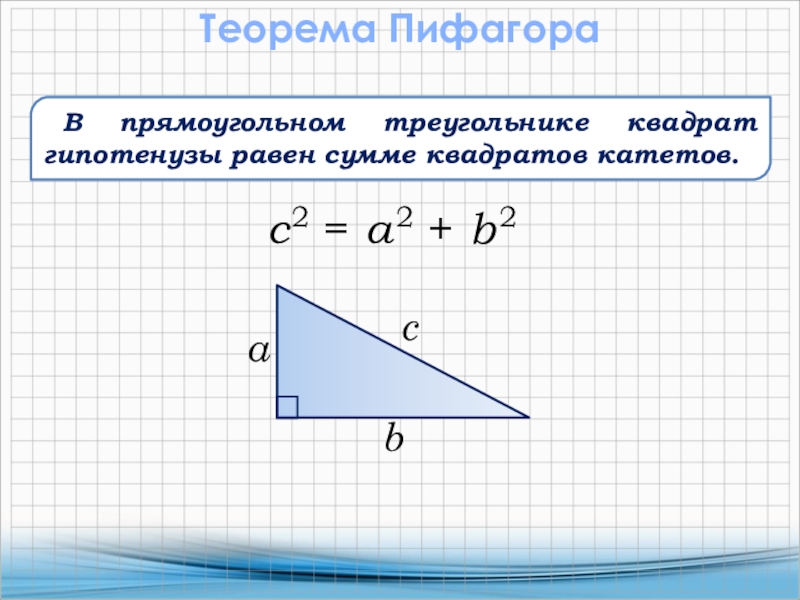
Слайд 2Теорема Пифагора
c 2 = a 2 + b 2
c
b
В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a
Слайд 3Задача №1
Дано: ∆АВС – п/у
АВ = 40, ВС = 32.
Найти: S∆ABC
Найдите
площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 32 и 40.
Решение:
Ответ: 384.
Слайд 4Дано: ∆АВС – р/б
АВ = 192, АС = ВС = 104.
Найти:
S∆ABC
Боковая сторона равнобедренного треугольника равна 104, а основание равно 192. Найдите площадь этого треугольника.
Решение:
Ответ: 3840.
Задача №2
Слайд 5Дано: ∆АВС – п/у
АВ = 92, А = 45°.
Найти: S∆ABC
В прямоугольном
треугольнике гипотенуза равна 92, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение:
Ответ: 2116.
Задача №3
Слайд 6Дано: ∆АВС – р/б
Р∆АВС = 338, АС = ВС = 97.
Найти:
S∆ABC
Периметр равнобедренного треугольника равен 338, а боковая сторона – 97. Найдите площадь треугольника.
Решение:
Ответ: 4680.
Задача №4
Слайд 7Дано: ∆АВС – р/б
Р∆АВС = 288, АВ = 140.
Найти: S∆ABC
Периметр равнобедренного
треугольника равен 288, а основание – 140. Найдите площадь треугольника.
Решение:
Ответ: 1680.
Задача №5
Слайд 10Найти: ВМ.
Решение:
Ответ: 24.
Задача №7
В треугольнике АВС АВ = ВС =
25, АС = 14. Найдите длину медианы ВМ.
Дано: ∆АВС – р/б
АВ = ВС = 25, АС = 14, АМ = МС.
Слайд 11Задача №8
Дано: АВСD – квадрат
АС = 46.
Найти: SABCD
Найдите площадь квадрата, если
его диагональ равна 46.
Решение:
Ответ: 1058.
Слайд 12Задача №9
Дано: АВСD – р/б трапеция
АВ = 29, DС =
19, AD = ВС = 13.
Найти: SABCD
Решение:
Ответ: 288.
Основания равнобедренной трапеции равны 19 и 29, а ее боковые стороны равны 13. Найдите площадь трапеции.
Слайд 13Задача №10
Дано: АВСD – прямоугольник
ВС = 48, АС = 50.
Найти:
SABCD
В прямоугольнике одна сторона равна 48, а диагональ равна 50. Найдите площадь прямоугольника.
Решение:
Ответ: 672.
Слайд 14Задача №11
Дано: АВСD – ромб
АВ = 87, АС = 126.
Найти:
SABCD
Сторона ромба равна 87, а диагональ равна 126. Найдите площадь ромба.
Решение:
Ответ: 7560.
Слайд 15Задача №12
Дано: АВСD – ромб, ВН – высота,
АН = 5, HD
= 8.
Найти: SABCD
Высота ВН ромба АВСD делит его сторону AD на отрезки HD = 8, АН = 5. Найдите площадь ромба.
Решение:
Ответ: 156.
Слайд 16Задача №13
Дано: АВСD – ромб, ВН – высота,
АН = 1, HD
= 28, BD = 53.
Найти: SABCD
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Ответ: 1305.
