- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Построение сечений многогранников
Содержание
- 1. Презентация по математике на тему Построение сечений многогранников
- 2. Аксиомы стереометрии
- 3. аАВАВС
- 4. Следствия из аксиом стереометрии
- 5. СеченияПлоскость, по обе стороны от которой имеются
- 6. Сечения пирамидыАВСDSСечение плоскостью, проходящей
- 7. 3. Сечение пирамиды плоскостью, параллельной основанию – многоугольник.ABCDSMNKPMNKP - сечение
- 8. Основные методы построения сечений многогранниковСуществует два основных метода построения сечений многогранников
- 9. Аксиоматические методы
- 10. Дано: трехгранная призма АВСА1В1С1. D Є A1C1,E
- 11. ABCA1B1C1DEFGLПостроение:1.D и E Є пл-ти грани АА1С1С
- 12. Алгоритм построения сечения методом следов1.Выяснить имеются ли
- 13. Метод внутреннего проектирования Метод внутреннего проектирования является
- 14. Пример 2ABC . .RMF .PDEДано:РАВСDE - пирамида.
- 15. Построение :1.Соединим R и M, т.к. они
- 16. Алгоритм построения сечения методом внутреннего проектирования1.Построить вспомогательные
- 17. Комбинированный методСущность этого метода состоит в том,
- 18. Правила для самоконтроля:Если многогранник выпуклый, то сечение
- 19. Практическое применениеГеометрические сечения широко применяются в строительстве,
- 20. 1.Какой из многоугольников не может получиться в сечении куба плоскостью?а) пятиугольникб) семиугольникв) шестиугольникг) трапеция
- 21. 2.Какая из закрашенных фигур является сечением многогранника?а)б)в)Т
- 22. 3.Дан тетраэдр DАВС. Плоскость МNL совпадает с плоскостью…а) АВСб) АВб) АВDв) ВСв) ВСDг) Аг) АDг) АDСАВСDLMN
- 23. 4.Дан тетраэдр DАВС . В плоскостях каких
- 24. 5.Дан тетраэдр DAВС . Точка М лежит
- 25. 6.Точка пересечения прямой МL и плоскости АВD
- 26. 7.Дан тетраэдр DABC. Точка N лежит на
- 27. 8.Дан тетраэдр АВС . Точка М лежит
- 28. ЗАДАЧИ
- 29. ЗАДАЧА 1Построение:1). Соединим т.P и т.Q (т.к.
- 30. Задача 2АВСDA1B1D1RPQДано :АВСDA1B1C1D1 – кубR Є A1B1,
- 31. АВСDA1B1C1D1RPQEFGHПостроение:1.Соединим точки P и Q, т.к. они
- 32. MQPЗадача 3Дано:SABCD – пирамидаМ Є SAQ Є SDP Є SCПостроить сечение, проходящее через три заданные точки
- 33. MPQЕFGHПостроение:1.Точки M и Q Є пл-ти ASD
- 34. ЕРСАВLKDЗадача 4Дано:РАВСDЕ- пирамидаК Є РЕL – след
- 35. Построение:1.ЕА ∩ L = T1.2.Построим КТ1. КТ1
- 36. ЗАДАЧА5ABCDEA1B1C1D1E1.MLДано:АВСDEA1B1C1D1E1 – призма М Є DD1L –
- 37. ABCDEA1B1C1D1E1.MLX.N.Y.P.Z..QT.RПостроение:1.DC ∩ L = X. MX ∩
- 38. A1(Q’)QRPC1C2CDD1BB1R’P’S1S2S3VB2Задача 6Дано: четырёхугольная призма ABCDA1B1C1D1 и точки
- 39. AA1BB1CC1DD1FF1NPMU1UVV1KQЗАДАЧА7Дано: призма ABCDFA1B1C1D1F1, точки Р – на
- 40. DAA1BB1CC1D1XNPYFUTZMN1QRSP1ЗАДАЧА8Дано: параллелепипед ABCDA1B1C1D1 и точки : М
- 41. Верный ответ!
- 42. Неверный ответ!
Слайд 1Тема урока: «Построение сечений многогранников»
Учитель математики высшей квалификационной категории Сидоренко Н.А.
Слайд 2Аксиомы стереометрии
А 1. Через
А 2. Через любые три точки пространства, не лежащие на одной прямой, проходит единственная плоскость.
А 3. Если две плоскости имеют общую точку, то они пересекаются по прямой.
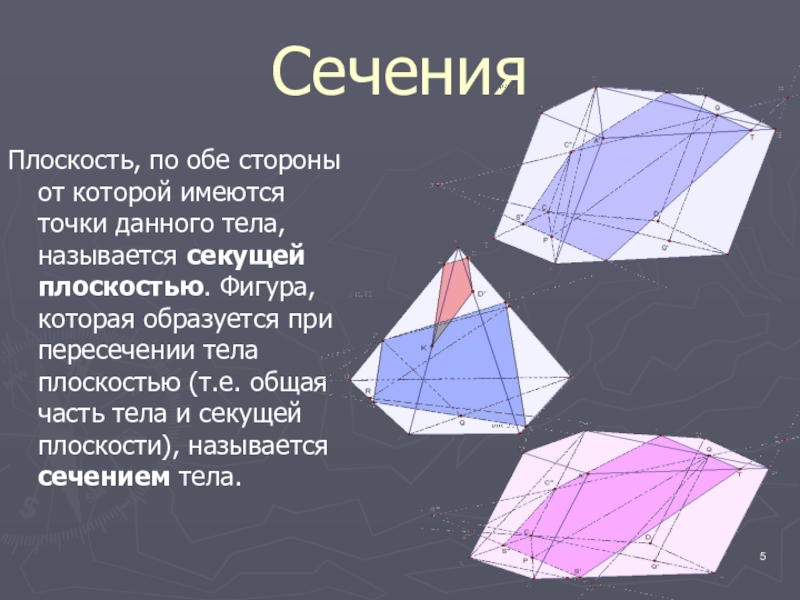
Слайд 5Сечения
Плоскость, по обе стороны от которой имеются точки данного тела, называется
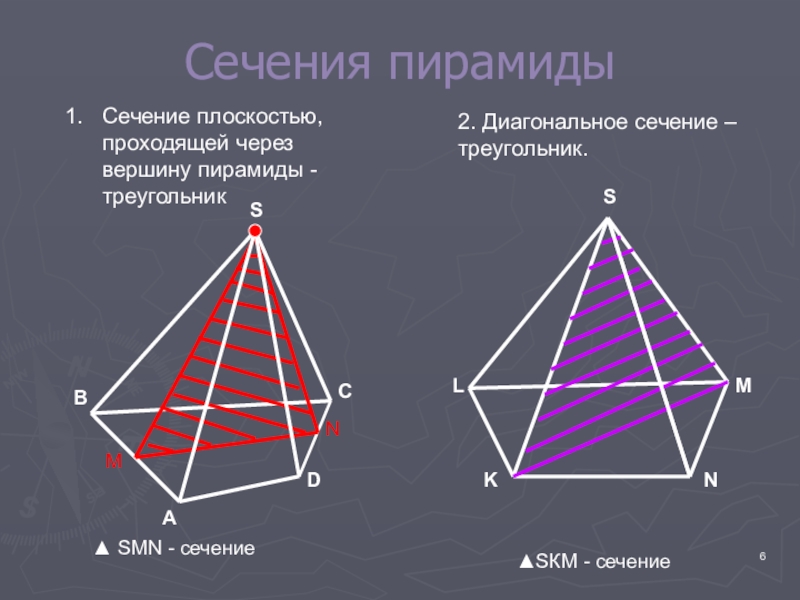
Слайд 6Сечения пирамиды
А
В
С
D
S
Сечение плоскостью,
проходящей через вершину пирамиды -
2. Диагональное сечение – треугольник.
K
L
M
N
S
M
N
▲SКM - сечение
▲ SMN - сечение
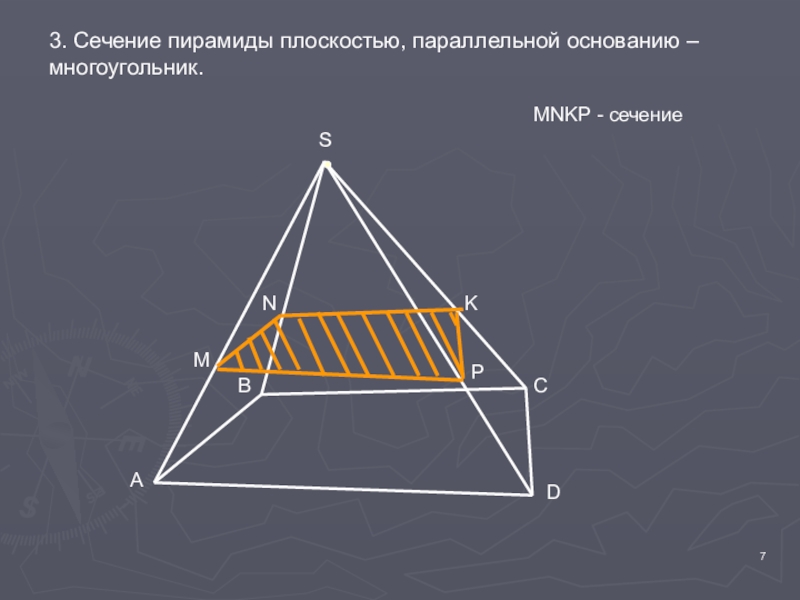
Слайд 73. Сечение пирамиды плоскостью, параллельной основанию – многоугольник.
A
B
C
D
S
M
N
K
P
MNKP - сечение
Слайд 8Основные методы построения сечений многогранников
Существует два основных метода построения сечений многогранников
Слайд 9Аксиоматические методы
Способ следов заключается в следующем. Вначале строят на основной плоскости след секущей плоскости (причем за основную плоскость принимают большей частью плоскость основания геометрического тела).Затем, используя след секущей плоскости, находят точки встречи ребер многогранника с секущей плоскостью. Используя полученные ( и данные ) точки, получают следы секущей плоскости на гранях многогранника.
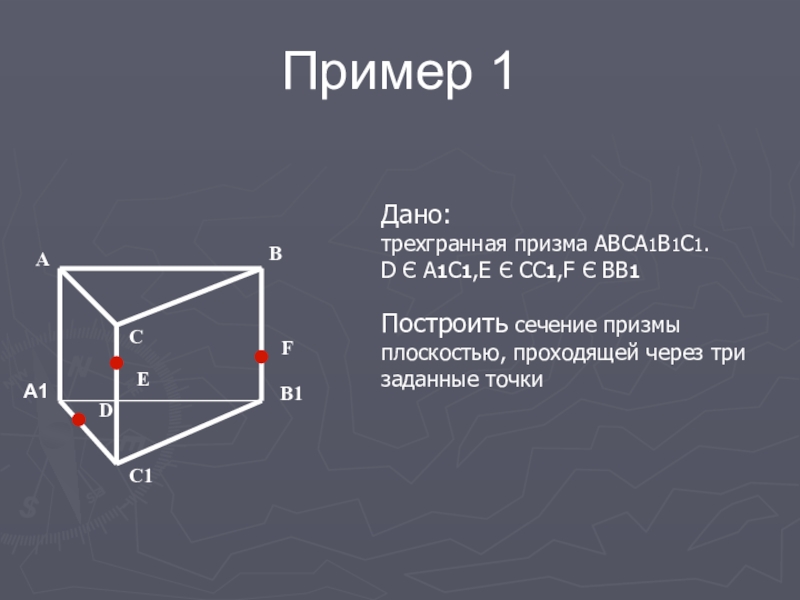
Слайд 10Дано: трехгранная призма АВСА1В1С1. D Є A1C1,E Є CC1,F Є BB1 Построить сечение призмы
A
B
C
B1
C1
D
E
F
Пример 1
A1
Слайд 11
A
B
C
A1
B1
C1
D
E
F
G
L
Построение:
1.D и E Є пл-ти грани АА1С1С и пл-ти
сечения =›
пл-тей.
2.Е и F Є пл-ти грани ВСС1В1 и пл-ти
сечения =› ЕF – линия пересечения этих пл-тей
3.DE и AA1 лежат в пл-ти АА1С1С.найдем их точку пересечения. АА1∩ DE = G
4. G Є пл-ти сечения, т.к. G Є DE. G и F Є пл-ти АА1В1В и пл-ти сечения =› GF – линия пересечения этих пл-тей.
5. GF ∩ А1В1 = L. F и L Є пл-ти АА1В1В и пл-ти сечения =› FL – линия пересечения этих пл-тей.
6. D и L Є А1В1С1 и пл-ти сечения =›
DL – линия пересечения этих пл-тей.
7. DEFL – искомое сечение.
Слайд 12Алгоритм построения сечения методом следов
1.Выяснить имеются ли в одной грани 2
2.Построить след сечения на плоскости основания многогранника.
3.Найти дополнительную точку сечения на ребре многогранника ( продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
4.Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения ее с ребрами грани.
5.Выполнить п.1
Слайд 13Метод внутреннего проектирования
Метод внутреннего проектирования является в достаточной мере универсальным.
Слайд 14Пример 2
A
B
C
.
.
R
M
F
.
P
D
E
Дано:
РАВСDE - пирамида. R Є PE, M
F Є PC.
Построить сечение пирамиды плоскостью, проходящей через точки R, M, F.
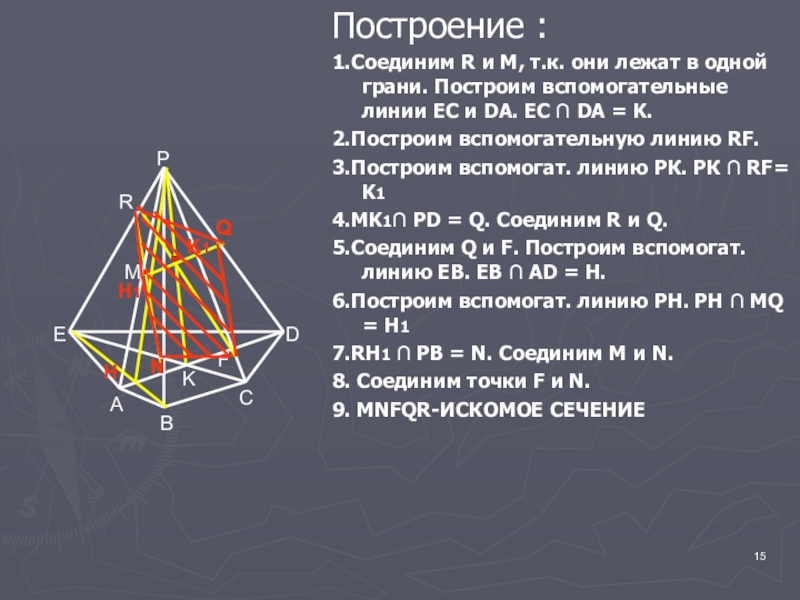
Слайд 15Построение :
1.Соединим R и M, т.к. они лежат в одной грани.
2.Построим вспомогательную линию RF.
3.Построим вспомогат. линию РК. РК ∩ RF= K1
4.MK1∩ PD = Q. Соединим R и Q.
5.Соединим Q и F. Построим вспомогат. линию ЕВ. ЕВ ∩ АD = H.
6.Построим вспомогат. линию РН. РН ∩ МQ = H1
7.RH1 ∩ PB = N. Соединим М и N.
8. Соединим точки F и N.
9. MNFQR-ИСКОМОЕ СЕЧЕНИЕ
P
A
B
C
D
E
.
.
.
R
M
F
K
.
K1
Q
H
H1
N
Слайд 16Алгоритм построения сечения методом внутреннего проектирования
1.Построить вспомогательные сечения и найти линию
2.Построить след сечения на ребре многогранника.
3.Если точек сечения не хватает для построения сечения, повторить пп.1-2.
Слайд 17Комбинированный метод
Сущность этого метода состоит в том, что на некоторых этапах
Слайд 18Правила для самоконтроля:
Если многогранник выпуклый, то сечение выпуклый многоугольник.
Вершины многоугольника всегда
Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.
Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении.
Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника.
Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.
Слайд 19Практическое применение
Геометрические сечения широко применяются в строительстве, архитектуре, мостостроении, технике, а
Слайд 201.Какой из многоугольников не может получиться в сечении куба плоскостью?
а) пятиугольник
б)
в) шестиугольник
г) трапеция
Слайд 223.Дан тетраэдр DАВС. Плоскость МNL совпадает с плоскостью…
а) АВС
б) АВб) АВD
в)
г) Аг) АDг) АDС
А
В
С
D
L
M
N
Слайд 234.Дан тетраэдр DАВС . В плоскостях каких граней лежит точка М?
а)
б) АВС и ВСб) АВС и ВСD
в) АВС и Ав) АВС и АDв) АВС и АDС
г) АВг) АВDг) АВD и АСг) АВD и АСD
А
В
С
D
M
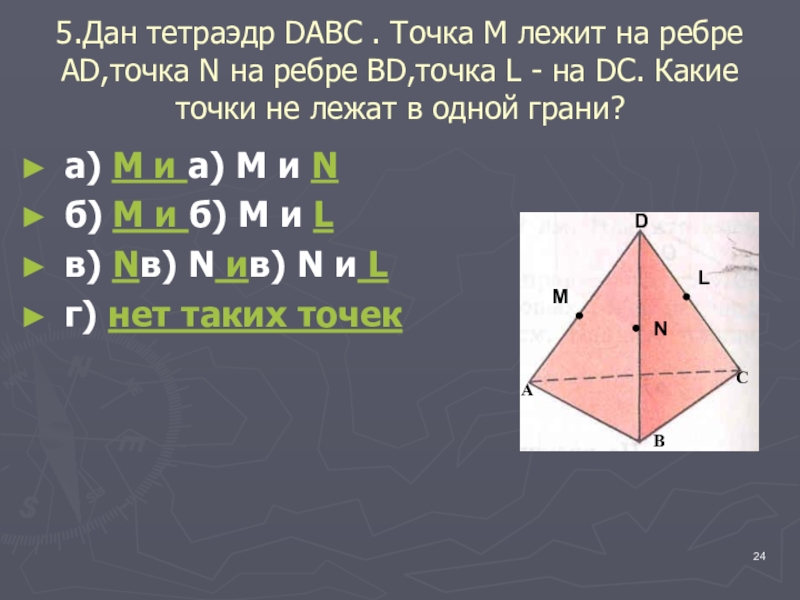
Слайд 245.Дан тетраэдр DAВС . Точка М лежит на ребре АD,точка N
а) М и а) М и N
б) М и б) М и L
в) Nв) N ив) N и L
г) нет таких точек
А
В
С
M
N
L
D
Слайд 256.Точка пересечения прямой МL и плоскости АВD лежит на пересечении прямых…
а)
б) Мб) МLб) МL и Сб) МL и СD
в) Мв) МL в) МL и Вв) МL и ВD
г) АВ и ВС
А
В
С
D
M
L
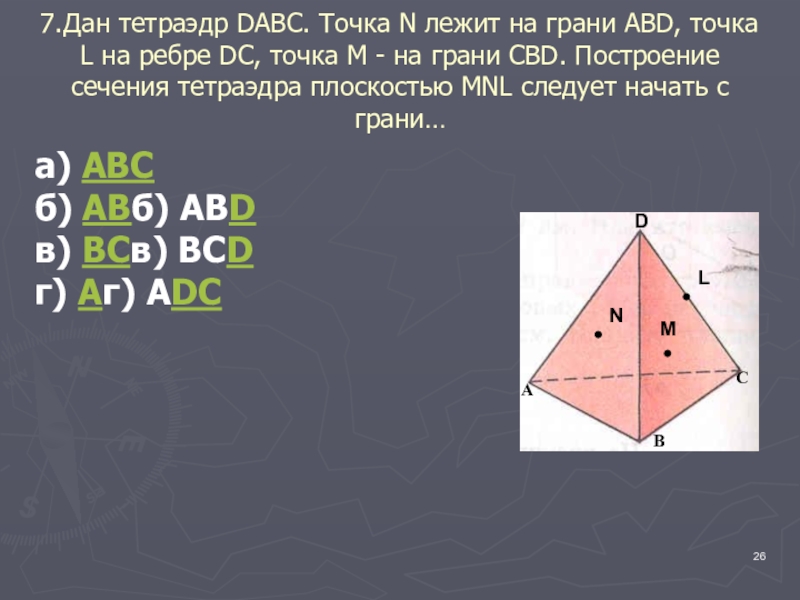
Слайд 267.Дан тетраэдр DABC. Точка N лежит на грани АВD, точка L
А
а) АВС
б) АВб) АВD
в) ВСв) ВСD
г) Аг) АDC
В
С
D
L
M
N
Слайд 278.Дан тетраэдр АВС . Точка М лежит на ребре АD, точка
а) ММN МN лежит в плоскости ВМN лежит в плоскости ВDМN лежит в плоскости ВDС
б) ММN МN пересекает плоскость ВМN пересекает плоскость ВDМN пересекает плоскость ВDС
в) Мв) МN в) МN параллельна плоскости Вв) МN параллельна плоскости ВDв) МN параллельна плоскости ВDС
г) Мг) МN г) МN скрещивается с Вг) МN скрещивается с ВDг) МN скрещивается с ВDС
А
В
С
D
M
N
Слайд 29ЗАДАЧА 1
Построение:
1). Соединим т.P и т.Q (т.к. они лежат в одной
2). Соединим т.Q и т.R (т.к. они лежат в одной плоскости EE1D1D). Получился отрезок QR.
3). Соединим т.R и т.P.
Треугольник PQR – искомое сечение данной призмы.
A1
B1
C1
D1
E1
F1
А
B
C
D
E
F
Дано: точки P, Q, R, лежащие на ребрах призмы. Построить сечение, проходящее через данные точки.
P
Q
R
Слайд 30Задача 2
А
В
С
D
A1
B1
D1
R
P
Q
Дано :
АВСDA1B1C1D1 – куб
R Є A1B1, Q Є DD1,
P
Построить
сечение куба плоскостью, походящей через три заданные точки
C1
Слайд 31
А
В
С
D
A1
B1
C1
D1
R
P
Q
E
F
G
H
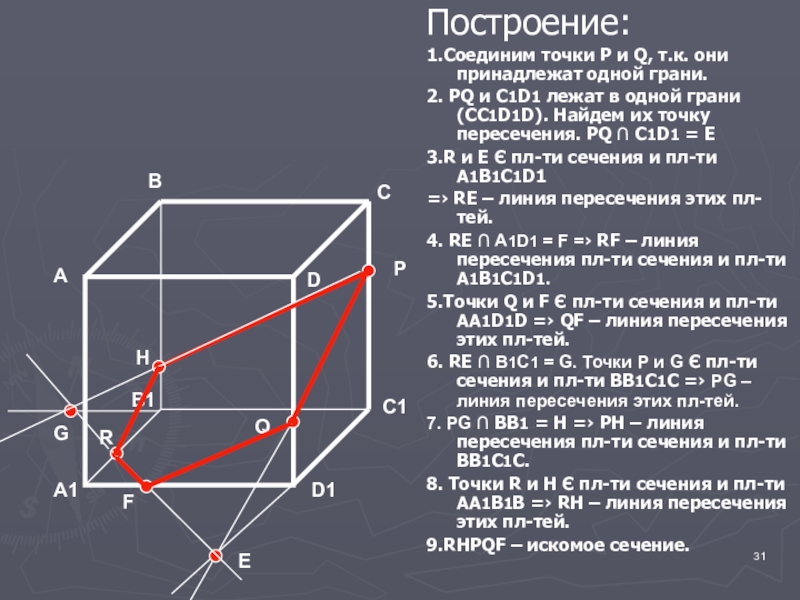
Построение:
1.Соединим точки P и Q, т.к. они принадлежат одной грани.
2. PQ
3.R и E Є пл-ти сечения и пл-ти A1B1C1D1
=› RE – линия пересечения этих пл-тей.
4. RE ∩ A1D1 = F =› RF – линия пересечения пл-ти сечения и пл-ти А1В1С1D1.
5.Точки Q и F Є пл-ти сечения и пл-ти АА1D1D =› QF – линия пересечения этих пл-тей.
6. RE ∩ В1С1 = G. Точки P и G Є пл-ти сечения и пл-ти ВВ1С1С =› PG – линия пересечения этих пл-тей.
7. PG ∩ ВВ1 = Н =› РН – линия пересечения пл-ти сечения и пл-ти ВВ1С1С.
8. Точки R и Н Є пл-ти сечения и пл-ти АА1В1В =› RН – линия пересечения этих пл-тей.
9.RHPQF – искомое сечение.
Слайд 32M
Q
P
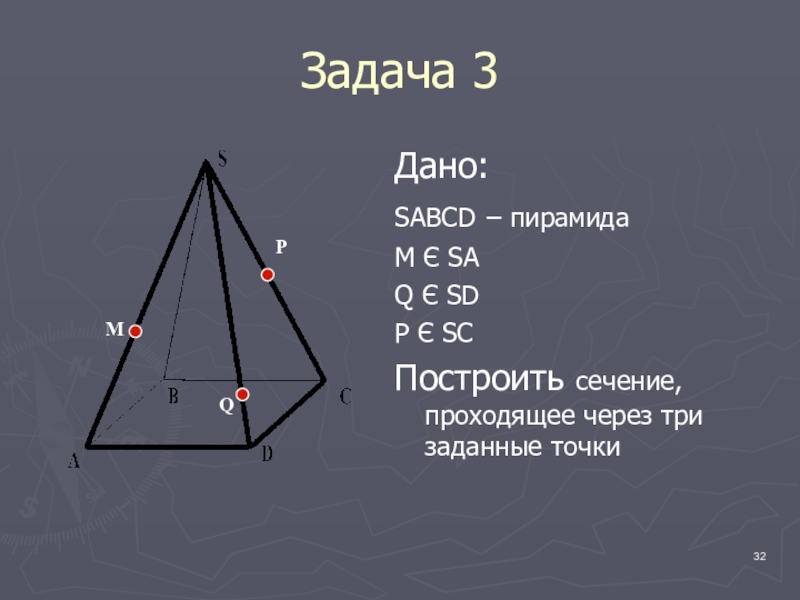
Задача 3
Дано:
SABCD – пирамида
М Є SA
Q Є SD
P Є SC
Построить сечение,
Слайд 33
M
P
Q
Е
F
G
H
Построение:
1.Точки M и Q Є пл-ти ASD =› MQ – линия
2. MQ ∩ AD = Е. РQ ∩ AD = F. Точки Е и F Є пл-ти сечения пл-ти АВС =› ЕF – линия пересечения этих пл-тей.
3. ЕF ∩ ВС = G. Точки Р и G Є пл-ти сечения и пл-ти ВSС =› РG – линия пересечения этих пл-тей.
4. РG ∩ ВS = Н. РН – линия пересечения пл-ти сечения и пл-ти ВSС
5. Точки М и Н Є пл-ти сечения и пл-ти ASВ =›
=› МН – линия пересечения этих пл-тей.
6. МНРQ – искомое сечение.
Слайд 34
Е
Р
С
А
В
L
K
D
Задача 4
Дано:
РАВСDЕ- пирамида
К Є РЕ
L – след пл-ти сечения.
Построить сечение пирамиды,
Слайд 35
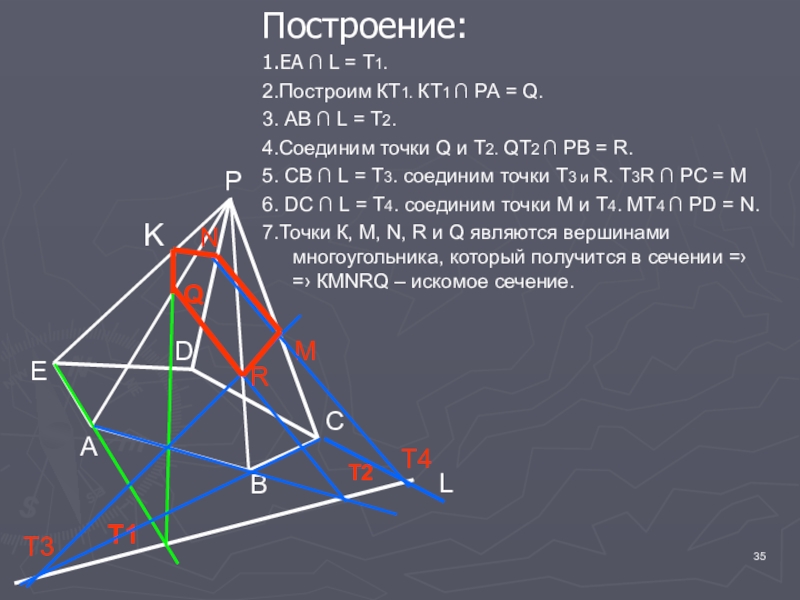
Построение:
1.ЕА ∩ L = T1.
2.Построим КТ1. КТ1 ∩ РА = Q.
3.
4.Соединим точки Q и Т2. QТ2 ∩ РВ = R.
5. СВ ∩ L = Т3. соединим точки Т3 и R. Т3R ∩ РС = М
6. DC ∩ L = Т4. соединим точки М и Т4. МТ4 ∩ РD = N.
7.Точки К, М, N, R и Q являются вершинами многоугольника, который получится в сечении =› =› КМNRQ – искомое сечение.
Е
Р
С
А
В
L
K
D
T1
Q
T2
R
T3
M
T4
N
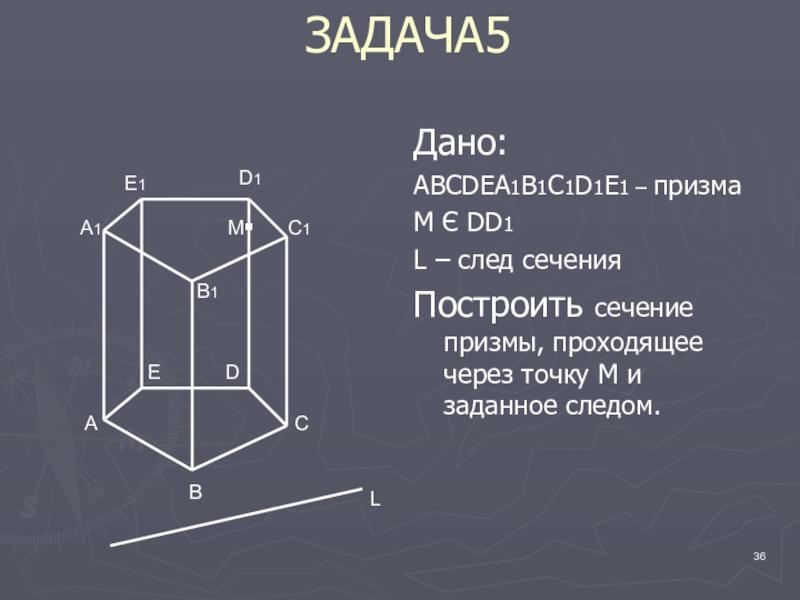
Слайд 36ЗАДАЧА5
A
B
C
D
E
A1
B1
C1
D1
E1
.
M
L
Дано:
АВСDEA1B1C1D1E1 – призма
М Є DD1
L – след сечения
Построить сечение призмы,
Слайд 37A
B
C
D
E
A1
B1
C1
D1
E1
.
M
L
X
.
N
.
Y
.
P
.
Z
.
.
Q
T
.
R
Построение:
1.DC ∩ L = X. MX ∩ CC1 = N.
2. CB
3. AB ∩ L = Z. Соединим Z и P. ZP ∩ АА1 = Q.
4. АЕ ∩ L = Т
5. TQ ∩ EE1 = R
6.Точки Q, R, M, N и P являются вершинами многоугольника, который получится в сечении.
7. QRMNP – искомое сечение.
.
Слайд 38
A1
(Q’)
Q
R
P
C1
C2
C
D
D1
B
B1
R’
P’
S1
S2
S3
V
B2
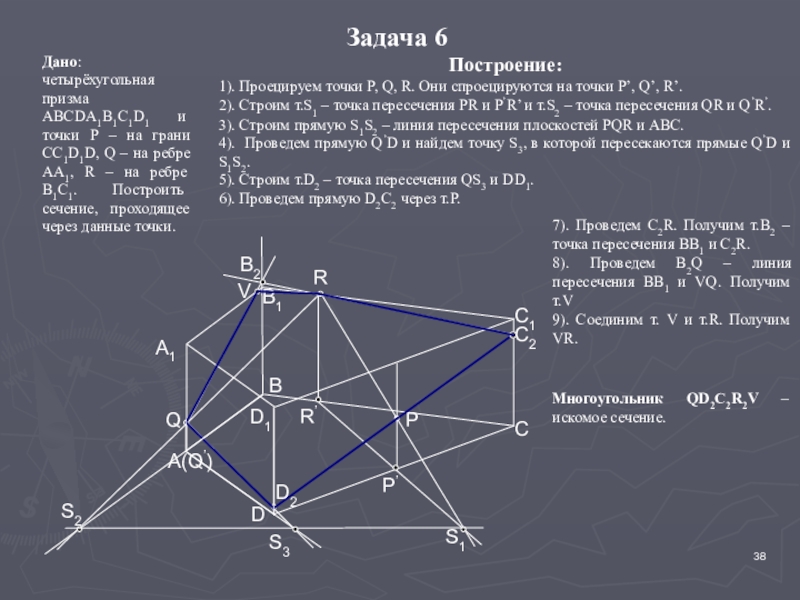
Задача 6
Дано: четырёхугольная призма ABCDA1B1C1D1 и точки Р – на грани
Построение:
1). Проецируем точки P, Q, R. Они спроецируются на точки P’, Q’, R’.
2). Строим т.S1 – точка пересечения PR и P’R’ и т.S2 – точка пересечения QR и Q’R’.
3). Строим прямую S1S2 – линия пересечения плоскостей PQR и ABC.
4). Проведем прямую Q’D и найдем точку S3, в которой пересекаются прямые Q’D и S1S2.
5). Строим т.D2 – точка пересечения QS3 и DD1.
6). Проведем прямую D2C2 через т.Р.
7). Проведем С2R. Получим т.В2 – точка пересечения ВВ1 и С2R.
8). Проведем В2Q – линия пересечения ВВ1 и VQ. Получим т.V
9). Соединим т. V и т.R. Получим VR.
Многоугольник QD2C2R2V – искомое сечение.
D2
A
Слайд 39A
A1
B
B1
C
C1
D
D1
F
F1
N
P
M
U1
U
V
V1
K
Q
ЗАДАЧА7
Дано: призма ABCDFA1B1C1D1F1, точки Р – на ребре СС1; N –
Построение:
1). Соединим т.P и т.N. Получим PN.
2). Соединим т.N и т.M. Получим NM.
3). Cсоединим т.P и т.М.
4). Спроецируем точки Р, N, M. Они спроектируются на точки С, D, F.
5). Соединим т.D и т.В. Получим, что DB и CF пересекаются в т.U1.
6). Спроецируем т.U1 на плоскость PNM. Получим т.U.
7). Спроецируем BD на плоскость PNM. Получим NQ.
8). Соединим т.D и т.A. Получим, что DA и CF пересекаются в т.V1.
9). Спроецируем т.V1 на плоскость PNM. Получим т.V.
10). Соединим т.V и т.N. Получим VN.
11). Спроецируем AD на плоскость PNM. Получим отрезок NK, который наложится на отрезок NV, т.е. NK является продолжением NV.
Пятиугольник KQPNM – искомое сечение данного куба.
Слайд 40D
A
A1
B
B1
C
C1
D1
X
N
P
Y
F
U
T
Z
M
N1
Q
R
S
P1
ЗАДАЧА8
Дано: параллелепипед ABCDA1B1C1D1 и точки : М – на грани ABCD,
Построение:
1). Спроецируем т.Р и т.N на плоскость ABCD. Получим точки P1, N1.
2). Соединим т. Р и т.N. Получим PN.
3). Соединим т.P1 и т.N1. Получим P1N1.
4). Продолжим PN и P1N1. Получим, что они пересекаются в т.X. 5).Соединим т.Х и т.М. Получим, что AD и XM пересекаются в т.Q,а ХМ пересекает CD в т.R.
6). Продолжим ВС и ХМ. Получим, что они пересекаются в т.У.
7). Соединим т.Р и т.У. Получим, что РУ пересекает ВС в т.S и в т.Т.
8). Продолжим ВВ1 и РУ. Получим, что они пересекаются в т.Z.
9). Соединим т.Z и т.Х. Получим, что XZ пересекается с А1B1 в т.U; XZ пересекается с AA1 в т.F.
Шестиугольник FUTSRQ – искомое сечение данного параллелограмма