- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Модуль геометрия
Содержание
- 1. Презентация по математике на тему Модуль геометрия
- 2. Теория к заданию №9
- 3. Теория к заданию №9 Биссектриса – отрезок,
- 4. Равнобедренный треугольник - треугольник, у которого две
- 5. Теория к заданию №9 Медиана:
- 6. Формулы нахождения площади треугольника: Средняя линия параллельна
- 7. Прямоугольный треугольник
- 8. 1. В треугольнике два угла равны
- 9. Ответ: 18.8. Сторона равностороннего треугольника равна 12√3.
- 10. Теория к заданию №10 Вписанная окружность:1. Центр
- 11. Описанная окружность 1. Центр окружности, описанной
- 12. Центральный и вписанный углы:
- 13. Четырехугольник ABCD вписан в окружность. Угол
- 14. Касательные в точках A и B
- 15. В треугольнике ABC известно, что AC
- 16. Теория к заданию №11 Правильный многоугольник:
- 17. Параллелограмм, все стороны которого равны называется ромбом.Четырёхугольник,
- 18. 11. Найдите площадь трапеции, изображённой на рисунке.Ответ: 168
- 19. Диагональ AC параллелограмма ABCD образует с его
- 20. В равнобедренной трапеции основания равны 3 и
- 21. Основания трапеции равны 10 и 11. Найдите
- 22. Разбор и решение задания №12 ОГЭ по
- 23. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линииОтвет: 6
- 24. На клетчатой бумаге с размером клетки 1×1 отмечены
- 25. Разбор типовых вариантов задания №13 ОГЭ
- 26. Ответ: 1,2Какие из следующих утверждений верны?
- 27. Ответ: 1,2Какие из следующих утверждений верны?1)
- 28. Слайд 28
Слайд 3Теория к заданию №9
Биссектриса – отрезок, выходящий из вершины треугольника и
Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
2. Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
3. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
Слайд 4Равнобедренный треугольник - треугольник, у которого две стороны равны.
Углы, при основании
Высота, проведенная из вершины, является биссектрисой и медианой.
Равносторонний треугольник - треугольник, у которого все стороны равны.
Все углы равны 60°.
2. Каждая из высот является одновременно биссектрисой и медианой.
3. Центры описанной и вписанной окружностей совпадают.
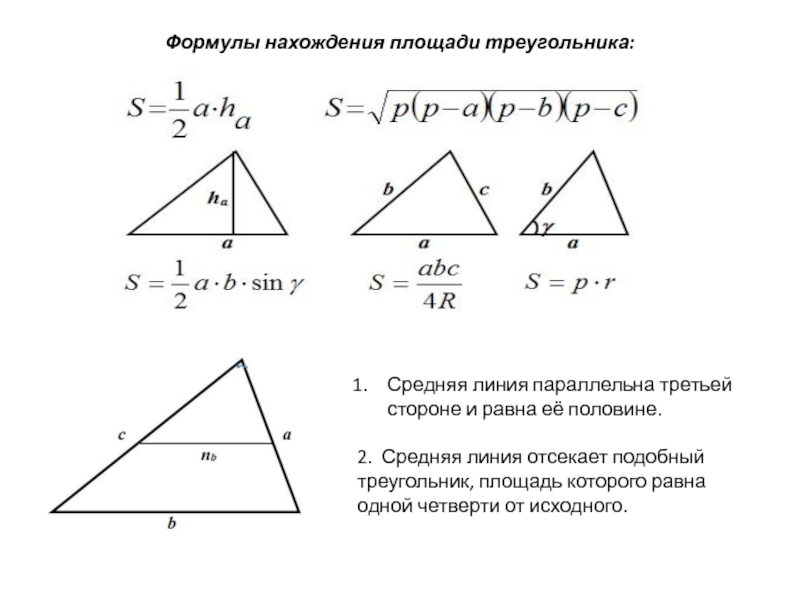
Слайд 6 Формулы нахождения площади треугольника:
Средняя линия параллельна третьей стороне и равна её
2. Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Слайд 8
1. В треугольнике два угла равны 73° и 48°. Найдите его
3. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Ответ: 32
3. В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Ответ: 29°
4. Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
подсказка: m = ( a • √3 )/ 2
5. Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
6. В треугольнике ABC известно, что AC = 56, BM - медиана, BM = 48. Найдите AM.
Ответ: 28
7. Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Ответ: 30.
Слайд 9Ответ: 18.
8. Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
9. Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Ответ: 20.
10. Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
Решение:
m = ( a • √3 )/ 2
a = ( 2 • m ) / √3
Ответ: 22
Слайд 10Теория к заданию №10
Вписанная окружность:
1. Центр окружности, вписанной в треугольник, лежит
3. Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d
Слайд 11Описанная окружность
1. Центр окружности, описанной около треугольника, лежит на пересечении
2. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
3. Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
4. Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.
Хорда – отрезок, соединяющий две точки окружности.
1. Диаметр, делящий хорду пополам, перпендикулярен хорде.
2. В окружности равные хорды равноудалены от центра окружности.
3. Отрезки пересекающихся хорд связаны равенством:
Слайд 13
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD
Ответ: 32°
Слайд 14
Касательные в точках A и B к окружности с центром O
Ответ: 1
Слайд 15
В треугольнике ABC известно, что AC = 16, BC = 12,
Ответ: 10
Слайд 17Параллелограмм, все стороны которого равны называется ромбом.
Четырёхугольник, у которого две стороны
Слайд 19Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35°
Ответ: 65
Слайд 20В равнобедренной трапеции основания равны 3 и 9, а один из
Слайд 21Основания трапеции равны 10 и 11. Найдите больший из отрезков, на
Ответ: 5,5
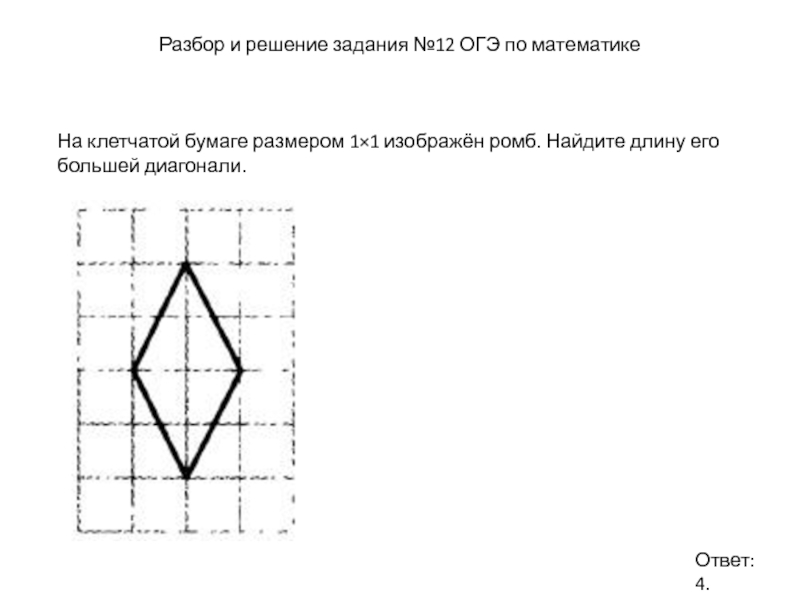
Слайд 22Разбор и решение задания №12 ОГЭ по математике
На клетчатой бумаге размером
Ответ: 4.
Слайд 23На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней
Ответ: 6
Слайд 24На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B
Ответ: 3.
Слайд 25
Разбор типовых вариантов задания №13 ОГЭ по математике
Какие из следующих утверждений
Все диаметры окружности всегда равны между собой - это даже интуитивно понятно. Что касается второго утверждения, то оно неверно - вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно - треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны. Ответ: 1,3.
Слайд 26
Ответ: 1,2
Какие из следующих утверждений верны?
1) Все высоты равностороннего треугольники равны.
2)
Слайд 27
Ответ: 1,2
Какие из следующих утверждений верны?
1) Длина гипотенузы прямоугольного треугольника меньше
2) Любой прямоугольник можно вписать в окружность.
3) Через заданную точку плоскости можно провести единственную прямую.
Первое утверждение верно из общих свойств треугольника - сумма двух сторон всегда больше третьей. Второе утверждение тоже верно - действительно, любой прямоугольник можно вписать в окружность. третье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.