- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Теорема Пифагора
Содержание
- 1. Презентация по геометрии Теорема Пифагора
- 2. Исторический экскурс Рассказ о ПифагореПифагор жил в
- 3. Из истории теоремы Пифагора Во времена самого
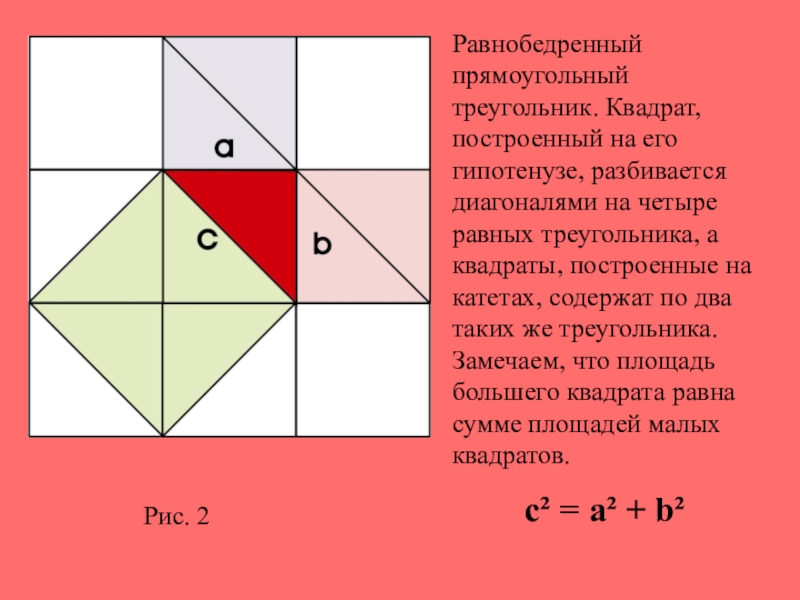
- 4. Рис. 2Равнобедренный прямоугольный треугольник. Квадрат, построенный на
- 5. Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его «ослиным мостом» или «бегством убогих»
- 6. aсbТеорема Пифагора занимает в геометрии особое место.
- 7. разминкаПо данным рисунка определите вид четырехугольникаКМNР
- 8. Теорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.bсаc² = a²+ b²
- 9. Забавное стихотворение , которое помогает запомнить формулировку
- 10. Закрепление материалаСВА21Вычислите, если возможно: а) сторону АС
- 11. СМFВ1в) вычислить диагональ ВМ квадрата ВСМF. (рис.
- 12. Решение старинных задачЗадача индийского математика XII в.
- 13. Если, обозначить глубину воды через х, то
- 14. Слайд 14
Исторический экскурс Рассказ о ПифагореПифагор жил в VI в. до н. э. в Древней Греции Основал философскую школу – пифагорейский союз.
Слайд 2Исторический экскурс
Рассказ о Пифагоре
Пифагор жил в VI в. до н. э.
в Древней Греции
Основал философскую школу – пифагорейский союз.
Основал философскую школу – пифагорейский союз.
Слайд 3Из истории теоремы Пифагора
Во времена самого ученого её формулировали так:
«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Или в виде задачи:
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах: S = S1 + S2».
Или в виде задачи:
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах: S = S1 + S2».
Слайд 4Рис. 2
Равнобедренный прямоугольный треугольник. Квадрат, построенный на его гипотенузе, разбивается диагоналями
на четыре равных треугольника, а квадраты, построенные на катетах, содержат по два таких же треугольника. Замечаем, что площадь большего квадрата равна сумме площадей малых квадратов.
с² = a² + b²
с² = a² + b²
Слайд 5Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его
«ослиным мостом» или
«бегством убогих»
«бегством убогих»
Слайд 6
a
с
b
Теорема Пифагора занимает в геометрии особое место. На основе теоремы можно
вывести или доказать большинство теорем. А еще она замечательна тем, что сама по себе вовсе не очевидна. Сколько ни смотри на прямоугольный треугольник, никак не увидишь, его стороны а, b и с связывает простое соотношение:
c² = a²+ b²
c² = a²+ b²
Слайд 8Теорема
Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
b
с
а
c² =
a²+ b²
Слайд 9Забавное стихотворение , которое помогает запомнить формулировку теоремы Пифагора.
Если дан нам
треугольник,
И при том с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
Слайд 10
Закрепление материала
С
В
А
2
1
Вычислите, если возможно:
а) сторону АС треугольника АВС. ( рис.
1)
Рис. 1
N
К
М
12
13
Рис. 2
б) сторону МN треугольника КМN. (рис. 2)
Слайд 11
С
М
F
В
1
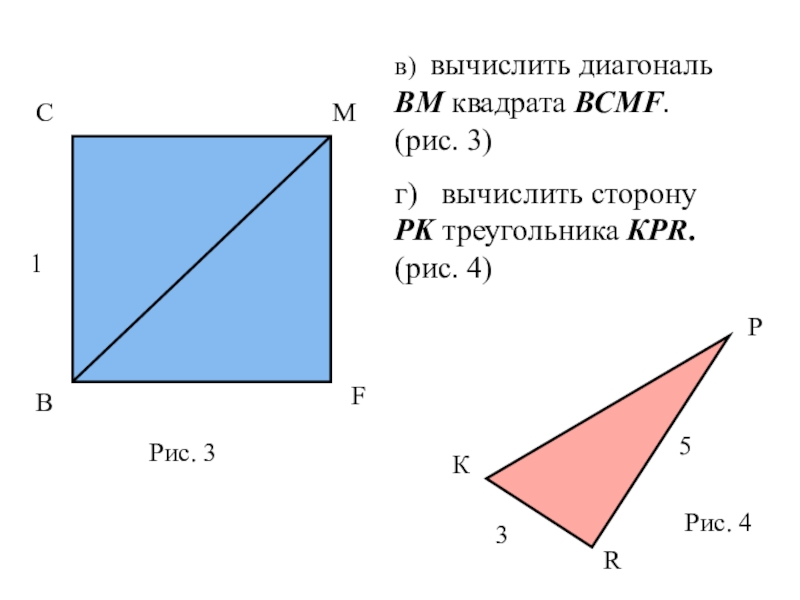
в) вычислить диагональ ВМ квадрата ВСМF. (рис. 3)
г) вычислить сторону
PK треугольника КPR. (рис. 4)
Рис. 3
К
P
R
3
5
Рис. 4
Слайд 12Решение старинных задач
Задача индийского математика XII в. Бхаскары.
На берегу реки рос
тополь одинокий.
Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута всего широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Слайд 13
Если, обозначить глубину воды через х, то получим прямоугольный треугольник,
один катет которого есть х, второй равен 5, а гипотенуза х+1.
1
х+1
х
(x+1)²=5²+x²
x²+2х+1=5²+x²
2х =25 – 1
2х = 24
х = 12.