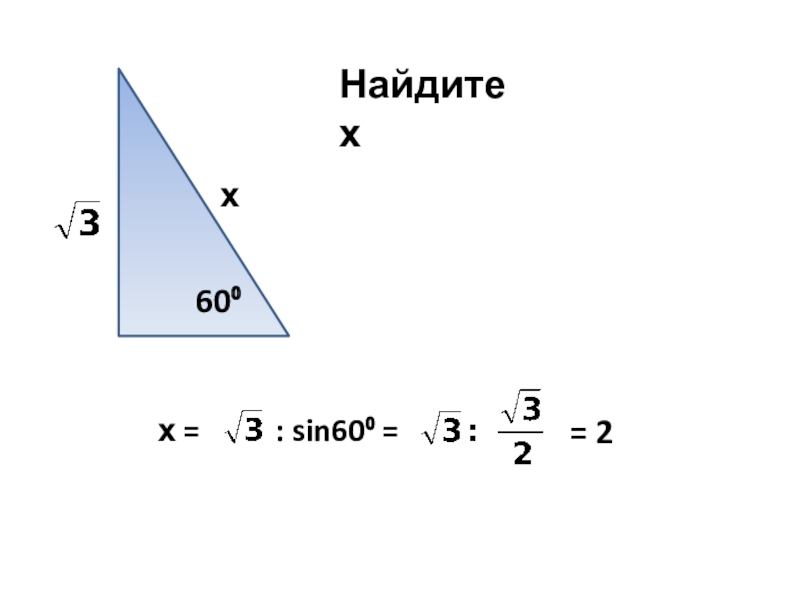- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Вычисление площади треугольника.
Содержание
- 1. Презентация по геометрии на тему Вычисление площади треугольника.
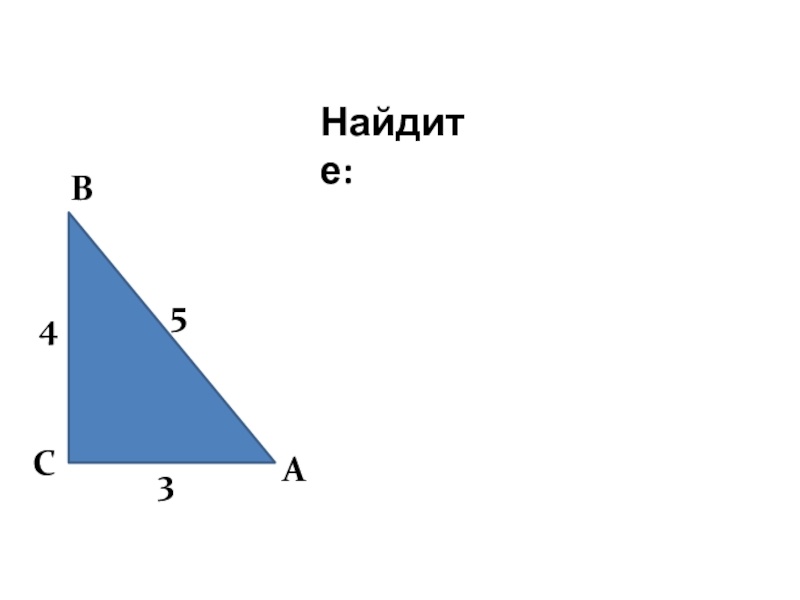
- 2. АВС453Найдите:
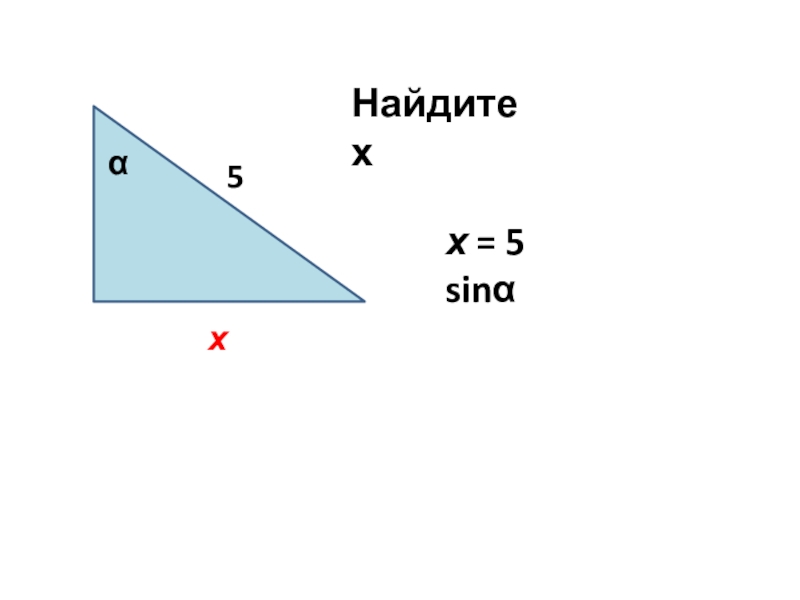
- 3. Найдите х5хαх = 5 sinα
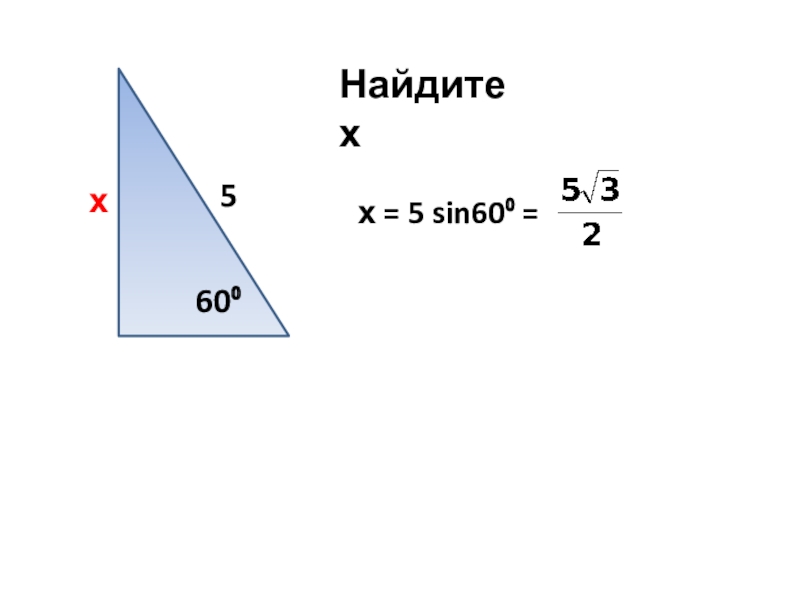
- 4. Найдите х5х60⁰х = 5 sin60⁰ =
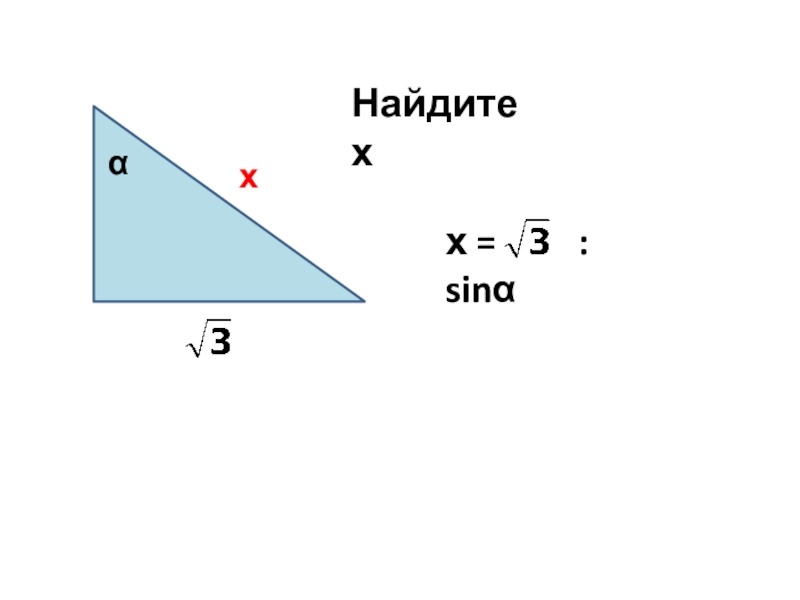
- 5. Найдите ххαх = : sinα
- 6. Найдите хх60⁰х = : sin60⁰ = = 2
- 7. А что называется треугольником? Треугольник - часть
- 8. Высоты треугольника называется перпендикуляр, опущенный из вершины
- 9. Чем равна площадь треугольника?Площадь треугольника равна
- 10. 07. 02. 2019Классная работаВычисление площади треугольника
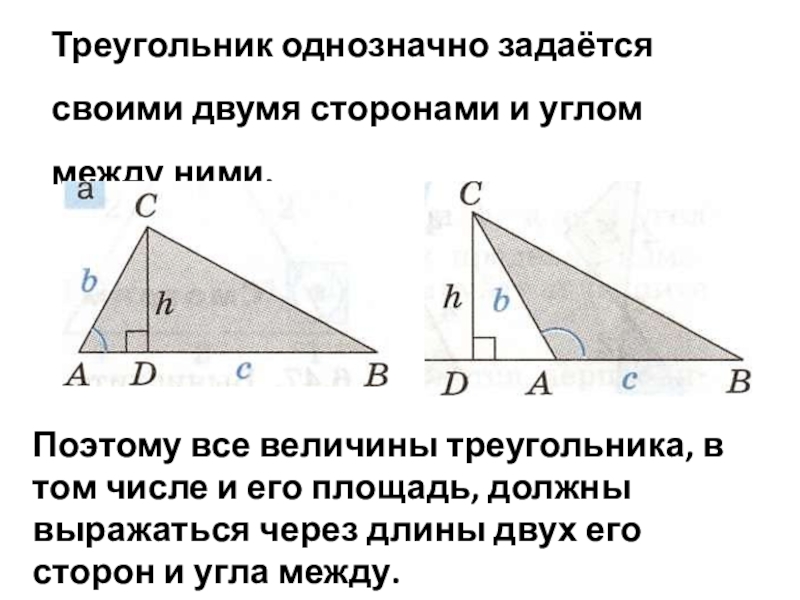
- 11. Треугольник однозначно задаётся своими двумя сторонами и
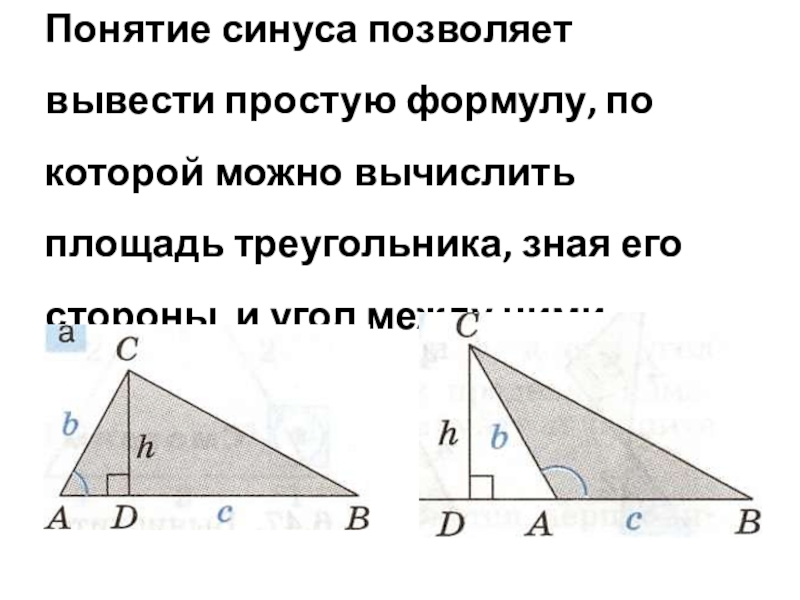
- 12. Понятие синуса позволяет вывести простую формулу, по
- 13. Рассмотрим ∆ АВС, у которого известны его
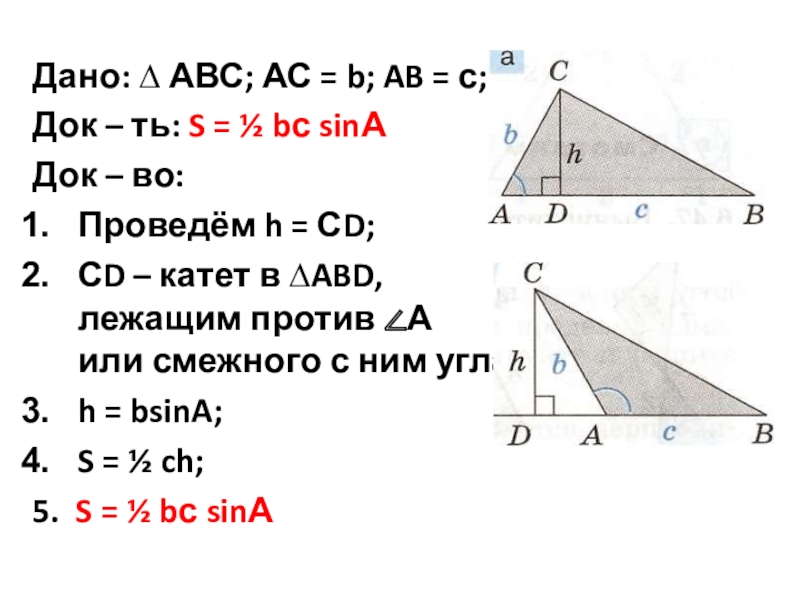
- 14. Дано: ∆ АВС; АС = b; AB
- 15. 6. 45Докажите, что площадь параллелограмма со сторонами
- 16. 6. 46Пусть ? — угол между диагоналями
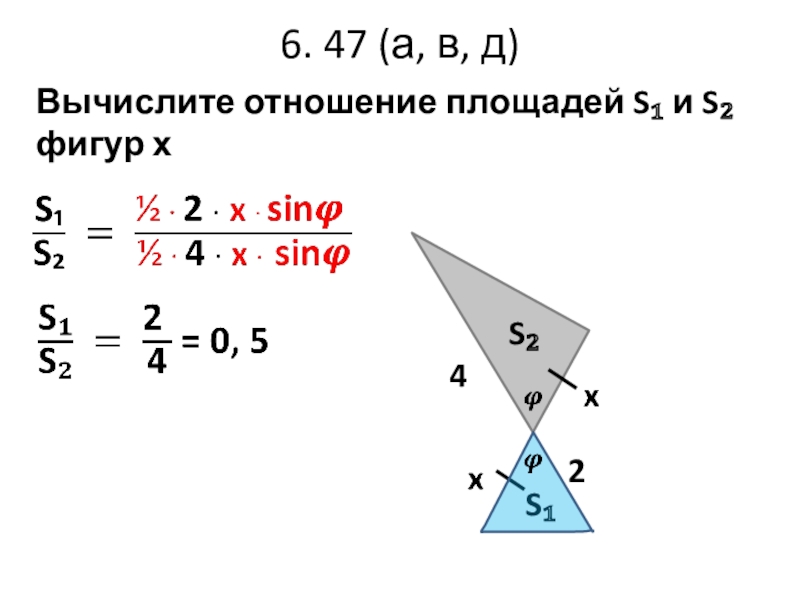
- 17. 6. 47 (а, в, д)Вычислите отношение площадей S₁ и S₂ фигур хS₂ S₁4 2
- 18. 6. 47 (а, в, д)Вычислите отношение площадей S₁ и S₂ фигурS₂ S₁5 3
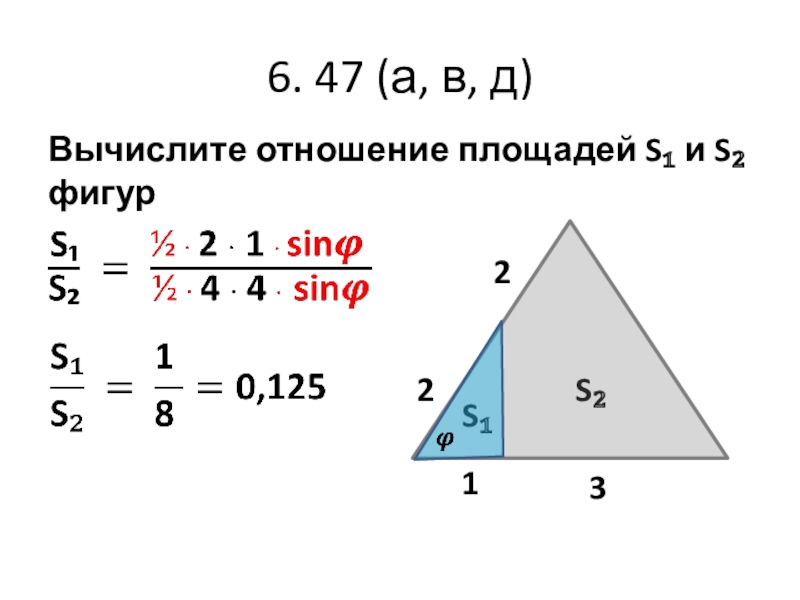
- 19. 6. 47 (а, в, д)Вычислите отношение площадей S₁ и S₂ фигурS₂ S₁ 3 221
- 20. 6.48(а, в, д, ж)Дано: ∆ АВС; АС
- 21. 6.48(а, в, д, ж)Дано: ∆ АВС; АС
- 22. 6.48(а, в, д, ж)Дано: ∆ АВС; АС
- 23. 6.48(а, в, д, ж)Дано: ∆ АВС; АС
- 24. 6.49(а, в, д)60°34
- 25. 6.49(а, в, д)Дано: АВСD; АB = 3;
- 26. 6.49(а, в, д)Дано: АВСD; АB = 3;
- 27. 6. 55 – Знать формулировку!Докажите, что биссектриса
- 28. Домашнее заданиеn. 6.5 – Выучить!№№ 6.48(б, г, е); 6.49(б, г, е)
АВС453Найдите:
Слайд 7А что называется треугольником?
Треугольник - часть плоскости ограниченной тремя отрезками,
соединяющие любые три точки не лежащие на одной прямой.
Слайд 8Высоты треугольника называется перпендикуляр, опущенный из вершины треугольника на его противоположную
сторону или её продолжение.
Перпендикуляр С Н1 проведённый к прямой АВ, - это отрезок,
один из концов которого (например точка Н1) принадлежит
прямой АВ и который образует с прямой АВ прямые углы.
А
В
С
Н1
Слайд 9 Чем равна площадь треугольника?
Площадь треугольника равна половине
произведения любой из его
сторон
и высоты, проведённой к этой стороне, т. е вычисляется по формуле .
и высоты, проведённой к этой стороне, т. е вычисляется по формуле .
Слайд 11Треугольник однозначно задаётся своими двумя сторонами и углом между ними.
Поэтому
все величины треугольника, в том числе и его площадь, должны выражаться через длины двух его сторон и угла между.
Слайд 12Понятие синуса позволяет вывести простую формулу, по которой можно вычислить площадь
треугольника, зная его стороны и угол между ними.
Слайд 13Рассмотрим ∆ АВС, у которого известны его стороны b, с и
∠ А между ними (рис. 160). Тогда его площадь S вычисляется по формуле
S = ½ bс sinА
S = ½ bс sinА
Слайд 14Дано: ∆ АВС; АС = b; AB = с;
Док – ть:
S = ½ bс sinА
Док – во:
Проведём h = СD;
СD – катет в ∆ABD, лежащим против ∠А или смежного с ним угла;
h = bsinA;
S = ½ ch;
5. S = ½ bс sinА
Док – во:
Проведём h = СD;
СD – катет в ∆ABD, лежащим против ∠А или смежного с ним угла;
h = bsinA;
S = ½ ch;
5. S = ½ bс sinА
Слайд 156. 45
Докажите, что площадь параллелограмма со сторонами
а и Ь и углом ? между ними вычисляется по формуле
S = bс sin?
S = bс sin?
Слайд 166. 46
Пусть ? — угол между диагоналями выпуклого четырёхугольника АВС D,
а S — его площадь. Докажите, что
S = ½ АС ∙ BD sin?
S = ½ АС ∙ BD sin?
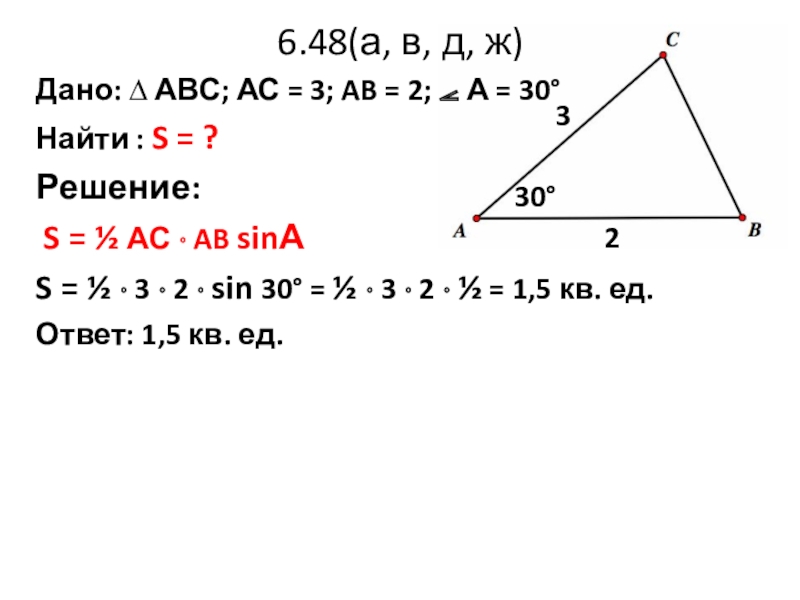
Слайд 206.48(а, в, д, ж)
Дано: ∆ АВС; АС = 3; AB =
2; ⦟ А = 30°
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 30° = ½ · 3 · 2 · ½ = 1,5 кв. ед.
Ответ: 1,5 кв. ед.
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 30° = ½ · 3 · 2 · ½ = 1,5 кв. ед.
Ответ: 1,5 кв. ед.
30°
2
3
Слайд 216.48(а, в, д, ж)
Дано: ∆ АВС; АС = 3; AB =
2; ⦟ А = 55°
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 55° = ½ · 3 · 2 · 0,819 ≈ 2,457 кв. ед.
Ответ: ≈ 2,457 кв. ед.
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 55° = ½ · 3 · 2 · 0,819 ≈ 2,457 кв. ед.
Ответ: ≈ 2,457 кв. ед.
55°
2
3
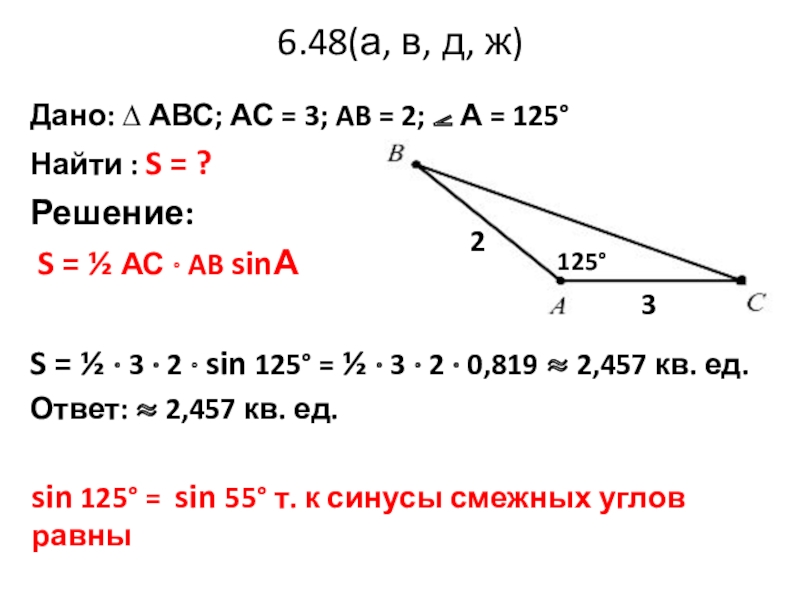
Слайд 226.48(а, в, д, ж)
Дано: ∆ АВС; АС = 3; AB =
2; ⦟ А = 125°
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 125° = ½ · 3 · 2 · 0,819 ≈ 2,457 кв. ед.
Ответ: ≈ 2,457 кв. ед.
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 125° = ½ · 3 · 2 · 0,819 ≈ 2,457 кв. ед.
Ответ: ≈ 2,457 кв. ед.
125°
2
3
sin 125° = sin 55° т. к синусы смежных углов равны
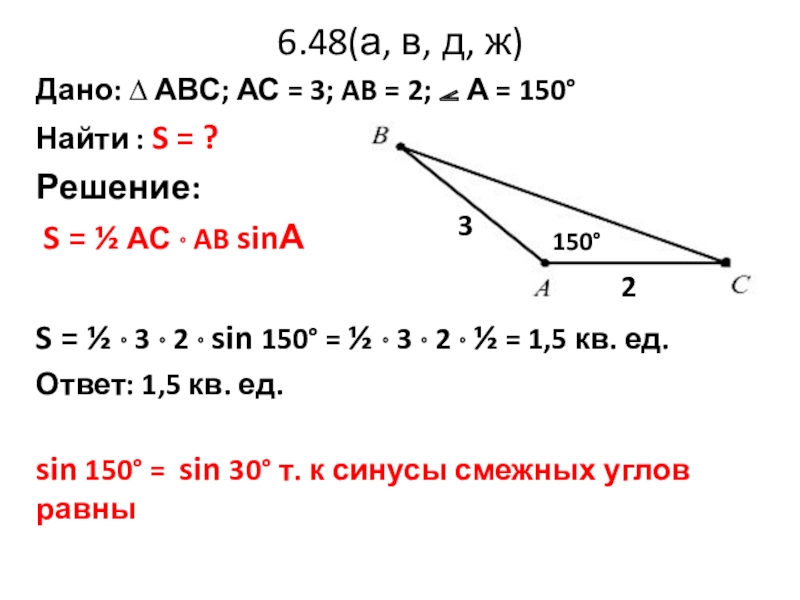
Слайд 236.48(а, в, д, ж)
Дано: ∆ АВС; АС = 3; AB =
2; ⦟ А = 150°
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 150° = ½ · 3 · 2 · ½ = 1,5 кв. ед.
Ответ: 1,5 кв. ед.
Найти : S = ?
Решение:
S = ½ АС · AB sinА
S = ½ · 3 · 2 · sin 150° = ½ · 3 · 2 · ½ = 1,5 кв. ед.
Ответ: 1,5 кв. ед.
150°
2
3
sin 150° = sin 30° т. к синусы смежных углов равны
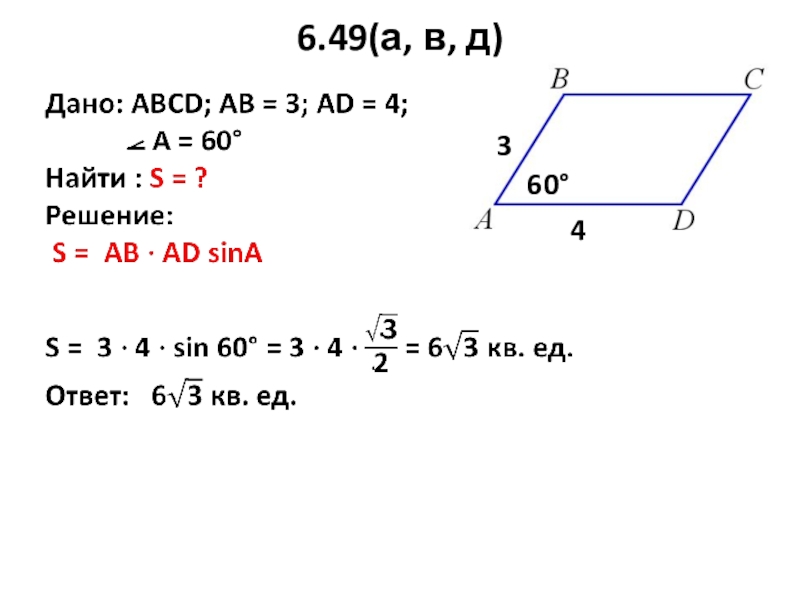
Слайд 256.49(а, в, д)
Дано: АВСD; АB = 3; AD = 4;
⦟ А = 80°
Найти : S = ?
Решение:
S = АB · AD sinА
S = 3 · 4 · sin 80° = 3 · 4 · 0,985 ≈ 11,82 кв. ед.
Ответ: ≈ 11, 82 кв. ед.
Найти : S = ?
Решение:
S = АB · AD sinА
S = 3 · 4 · sin 80° = 3 · 4 · 0,985 ≈ 11,82 кв. ед.
Ответ: ≈ 11, 82 кв. ед.
80°
3
4
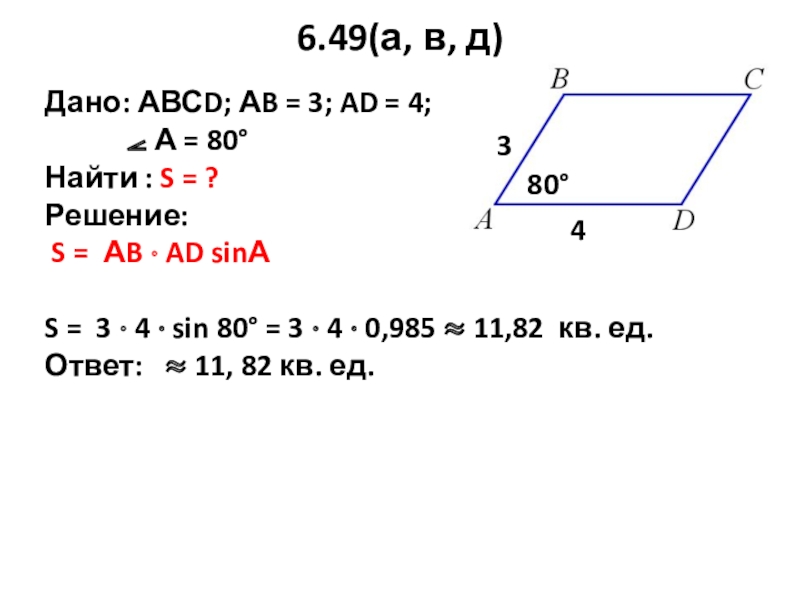
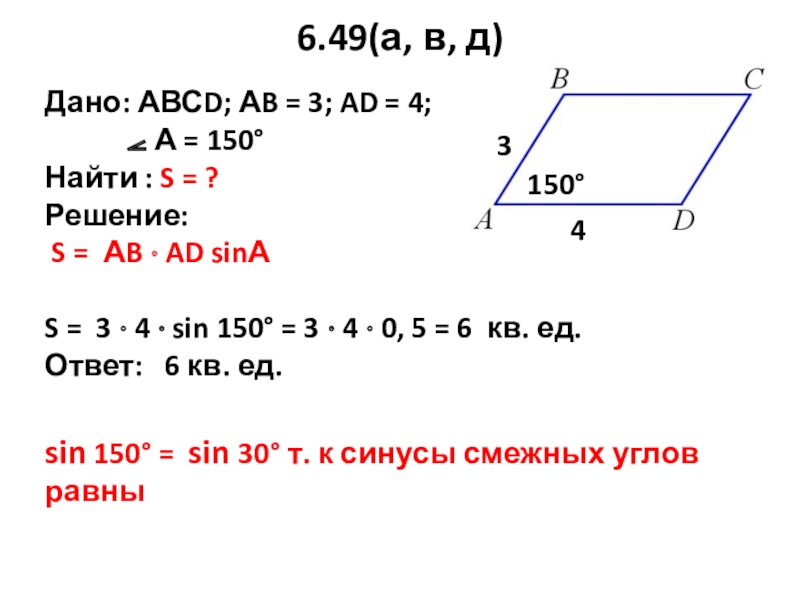
Слайд 266.49(а, в, д)
Дано: АВСD; АB = 3; AD = 4;
⦟ А = 150°
Найти : S = ?
Решение:
S = АB · AD sinА
S = 3 · 4 · sin 150° = 3 · 4 · 0, 5 = 6 кв. ед.
Ответ: 6 кв. ед.
Найти : S = ?
Решение:
S = АB · AD sinА
S = 3 · 4 · sin 150° = 3 · 4 · 0, 5 = 6 кв. ед.
Ответ: 6 кв. ед.
150°
3
4
sin 150° = sin 30° т. к синусы смежных углов равны
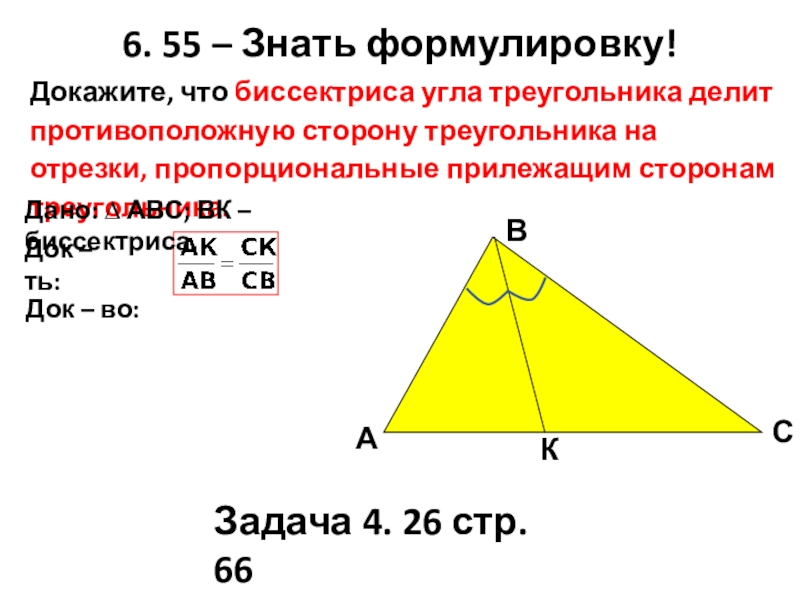
Слайд 276. 55 – Знать формулировку!
Докажите, что биссектриса угла треугольника делит противоположную
сторону треугольника на отрезки, пропорциональные прилежащим сторонам треугольника.
А
В
С
К
Дано: ∆ АВС; ВК – биссектриса.
Док – ть:
Док – во:
Задача 4. 26 стр. 66
