Презентация, доклад по геометрии на тему Построение точки пересечения прямой и плоскости и линии пересечения плоскостей

Сформулируйте А3.

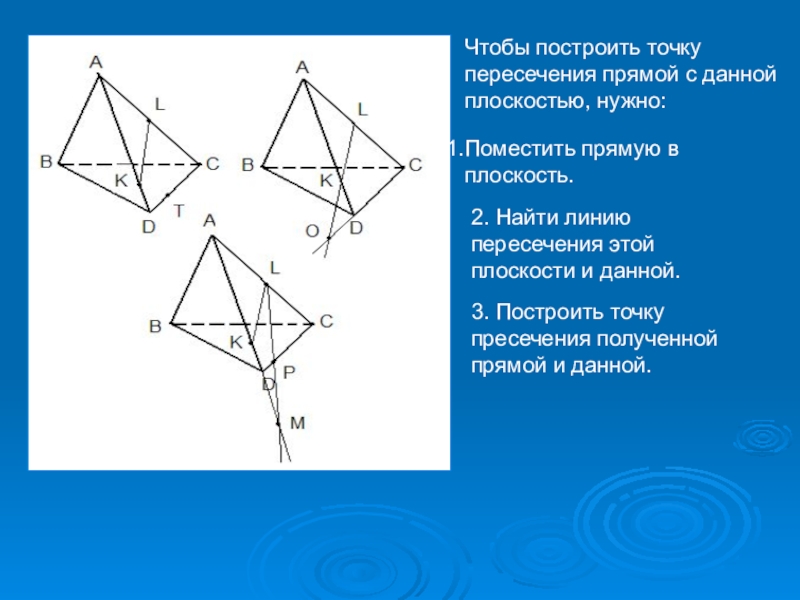
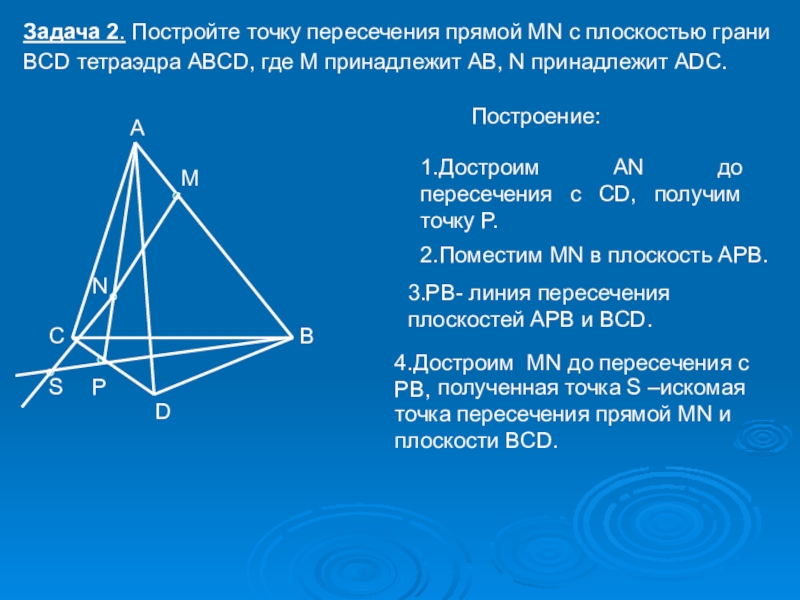
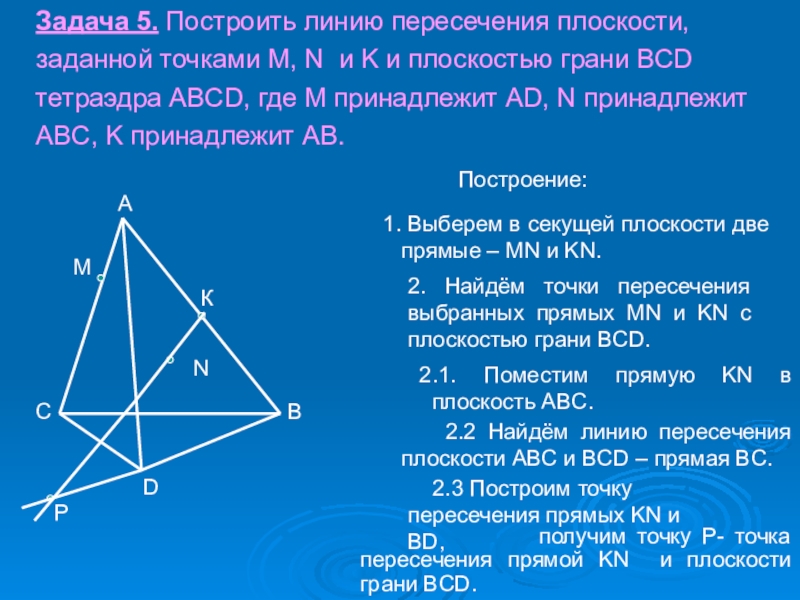
4. Могут ли прямая и плоскость иметь две общие точки?

5. Сколько плоскостей можно провести через три точки?

1. Назовите основные фигуры на плоскости.

2. Сформулируйте аксиому А1.

3. Сколько плоскостей можно провести через прямую и не лежащую на ней точку?

4. Сколько может быть общих точек у прямой и плоскости?

5. Могут ли прямая и плоскость иметь только одну общую точку?

две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

4. Могут.

5. если три точки лежат на одной прямой, то через них можно провести бесконечно много плоскостей; если три точки не лежат на одной прямой, то через них можно провести единственную плоскость

2.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

3. Одну

4. Если прямая пересекает плоскость, то одна; если лежит в плоскости, то бесконечно много; если параллельна плоскости, то ни одной;

5. Да

LK и CD.
в) KL с плоскостью ВСD.
г) LP и плоскости ABD.

а) DC и AB –не пересекаются.

б) О -точкой пересечения LK и CD.

в) KL пересекает плоскость BCD в точке О.

г) LP пересекает плоскость ABD в точке М.

в плоскость.

2. Найти линию пересечения этой плоскости и данной.

3. Построить точку пресечения полученной прямой и данной.

М и N. Постройте точки пересечения прямой MN с гранью BCD.

А

В

С

D

M

N

E

Построение:

1. Поместить прямую MN в плоскость ABD.

2. Линией пересечения плоскостей ABD и ВСD является ребро BD.

3. Достроим MN до пересечения с BD,

получим точку Е -искомая точка пересечения прямой MN и плоскости BCD.

тетраэдра ABCD, где M принадлежит AB, N принадлежит ADC.

M

N

Построение:

1.Достроим AN до пересечения с CD, получим точку P.

Р

2.Поместим MN в плоскость APB.

3.PB- линия пересечения плоскостей APB и BCD.

4.Достроим MN до пересечения с PB,

полученная точка S –искомая точка пересечения прямой MN и плоскости BCD.

S

в плоскость.

2. Построить (найти) линию пересечения этой плоскости и данной.

3. Построить точку пресечения полученной прямой и данной.

S – точка пересечения прямой MN с плоскостью грани BCD.

2. Построим линию пересечения плоскостей APQ и BCD. Так как P и Q являются общими точками этих плоскостей, то проводя прямую через эти точки, получим линию пересечения плоскостей APQ и BCD.

Задача 3. Постройте точку пересечения прямой MN с плоскостью грани BCD, где M принадлежит ABC, N принадлежит ADC.

M

N

Построение:

1. Поместим прямую MN в плоскость, для этого достроим AM и AN до пересечения с рёбрами CB и DC. Получим точки Q и P.

Р

Q

S

заданы точки M, N и K соответственно. Найти линию пересечения плоскостей BCD и MNK.

А

С

В

D

M

K

N

Построение:

1. Р -точка пересечения KN и DC

2. S-точка пересечения MN и BD.

3. PS – линия пересечения плоскостей BCD и MNK.

Р

S

2 прямые.

2. Найти точки пересечения выбранных прямых с плоскостью, которую пересекает заданная плоскость.

3.Полученные точки задают прямую, которая является следом секущей плоскости.

K и плоскостью грани BCD тетраэдра ABCD, где M принадлежит AD, N принадлежит ABC, K принадлежит AB.

М

К

N

Построение:

Выберем в секущей плоскости две прямые – MN и KN.

2. Найдём точки пересечения выбранных прямых MN и KN с плоскостью грани BCD.

.1. Поместим прямую KN в плоскость ABC.

2.2 Найдём линию пересечения плоскости ABC и BCD – прямая BC.

2.3 Построим точку пересечения прямых KN и BD,

получим точку Р- точка пересечения прямой KN и плоскости грани BCD.

Р

AN до пересечения с ВD,

получим точку Q. Плоскость АQD- есть та плоскость, которой принадлежит MN.

Q

2.5 Построим линию пересечения плоскостей АQC и BCD.

Для этого необходимо найти две общие точки этих плоскостей. Так как точка C является вершиной тетраэдра, то она принадлежит АQC и BCD, так как точка Q принадлежит АQC и BCD (так как Q принадлежит DB, а DB лежит в BCD), то CQ–линия пересечения плоскостей АQC и BCD.

2.6 Построим точку пересечения прямой MN и CQ.

S

S –точка пересечения прямой MN и плоскости BCD.

3. PS- искомая линия пересечения плоскости заданной точками M, N и K и плоскости грани BCD тетраэдра ABCD.

K и плоскостью грани BCD тетраэдра ABCD, где M принадлежит AB, N принадлежит ABC, K принадлежит ADC.

M

N

K

X

Y

P

S

в плоскость.

2. Построить (найти) линию пересечения этой плоскости и данной.

3. Построить точку пресечения полученной прямой и данной.

2 прямые.

2. Найти точки пересечения выбранных прямых с плоскостью, которую пересекает заданная плоскость.

3.Полученные точки задают прямую, которая является следом секущей плоскости.

точку пересечения прямой DР c плоскостью АВС.
в) построить линию пересечения плоскости АD1Р и АВВ1
г) вычислить длину отрезков АР и А D1, если АВ=а.



2. Задача . Построить линию пересечения плоскости, заданной точками M, N и K и плоскостью грани BCD тетраэдра ABCD, где M принадлежит ABD, N принадлежит ABC, K принадлежит ADC.