Выполнили: Свиридов Александр и Леонтьев Дмитрий
Руководитель: Лукьянова Ольга Георгиевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Формула Пика
Содержание
- 1. Презентация по геометрии на тему Формула Пика
- 2. "Геометрия - есть знание величин, фигур и
- 3. Актуальность: при решении задач по математике и
- 4. Гипотеза:мы считаем, что вычисление площадей сложных фигур
- 5. Объект исследования: формула Пика для вычисления площадей
- 6. Задачи: 1. Изучить методы вычисления площадей
- 7. Методы:3. Сравнение4. Поиск2. Обобщение1. Системный анализ
- 8. Основная часть Задача 1. 1 способ -
- 9. 2 способ – достраивание Задача 2. Решение:1)SABF
- 10. Задача 3 Решение:S1 = 4 *
- 11. Вывод: После решения этих задач мы поняли,
- 12. Георг Александр Пик -
- 13. В – внутренние узлы Г – граничные
- 14. Как пользоваться формулой Пика Задача 4.Решение:В = 1,
- 15. Вернёмся к задаче №3 и вычислим еёплощадь
- 16. Журнал «Квант» 1974 г.Задача про кузнечиков
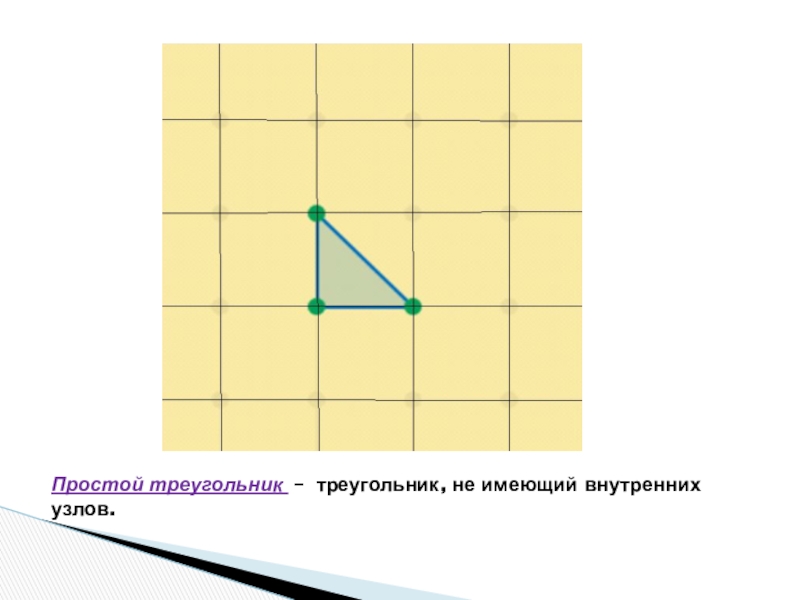
- 17. Простой треугольник – треугольник, не имеющий внутренних узлов.
- 18. Слайд 18
- 19. Слайд 19
- 20. Вывод:Площадь треугольника при прыжке одного кузнечика
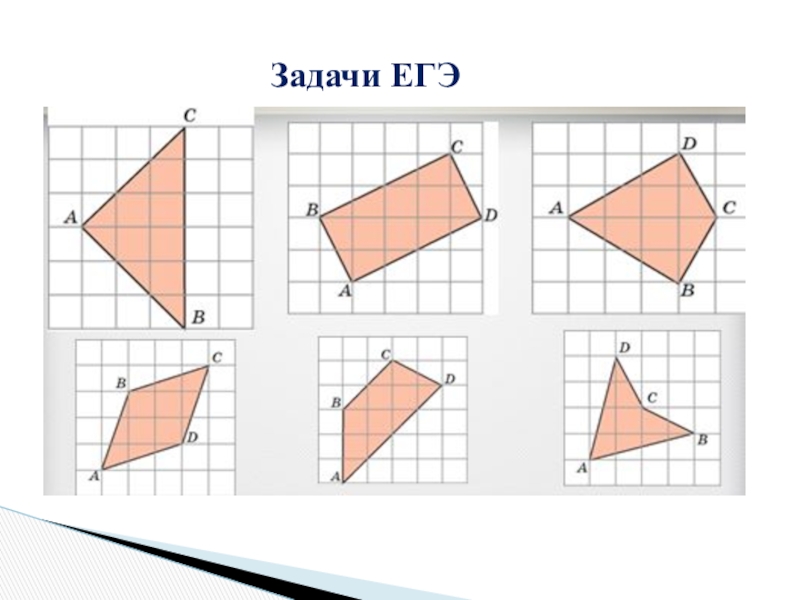
- 21. Задачи ЕГЭ
- 22. Задача 5 1 способ:Решение достраиванием:1. S1 =
- 23. 2 способ:Решение с помощью Формулы Пика: Г
- 24. Задача 6Решение с помощью Формулы Пика: Г =
- 25. Задача 7Решение с помощью Формулы Пика:Г =
- 26. Проверили вычисления с помощью компьютерной программы сайта «Математические этюды» www.etudes.ru/ru/etudes/pick-theorem/
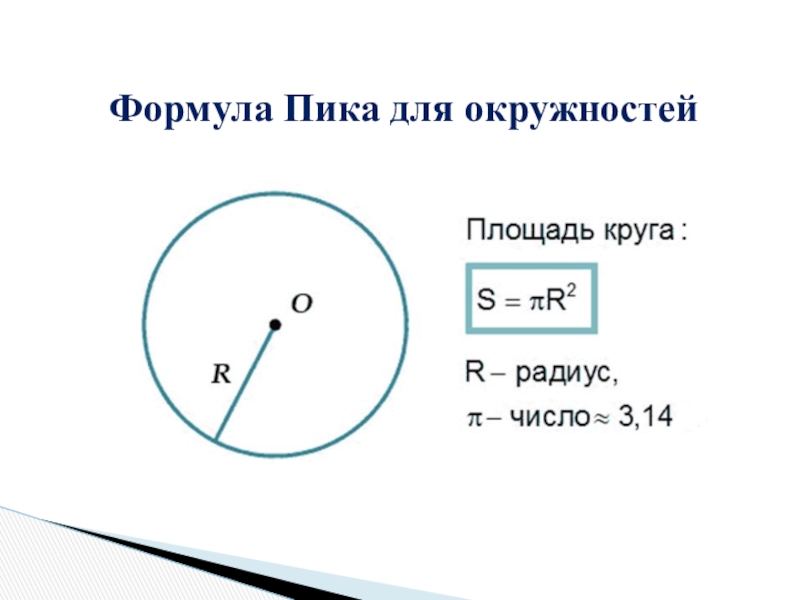
- 27. Формула Пика для окружностей
- 28. Решение по формуле: Sкол = ?R12 -
- 29. Решение по формулеПика:В1= 21
- 30. Формула Пика в пространстве
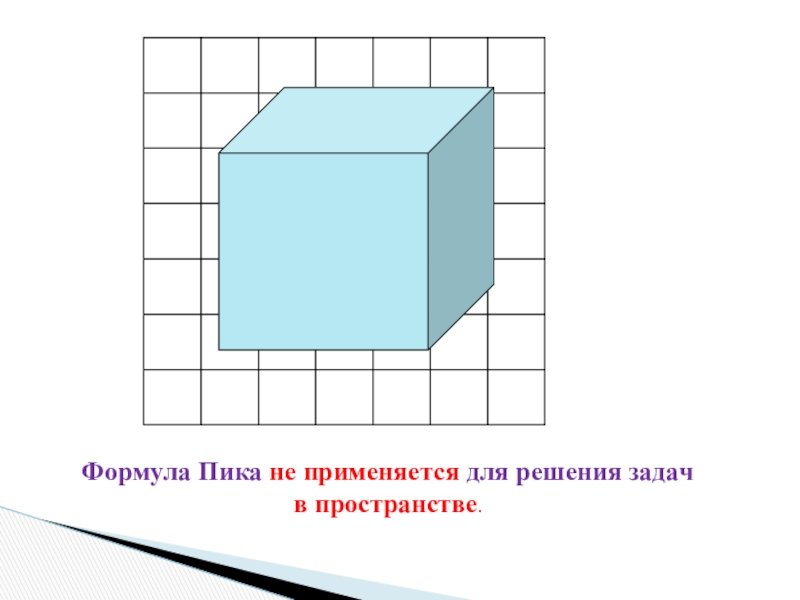
- 31. Формула Пика не применяется для решения задач в пространстве.
- 32. Задача 1: Рассчитать общую площадь школы, используя
- 33. Масштаб 1 : 4001 см2
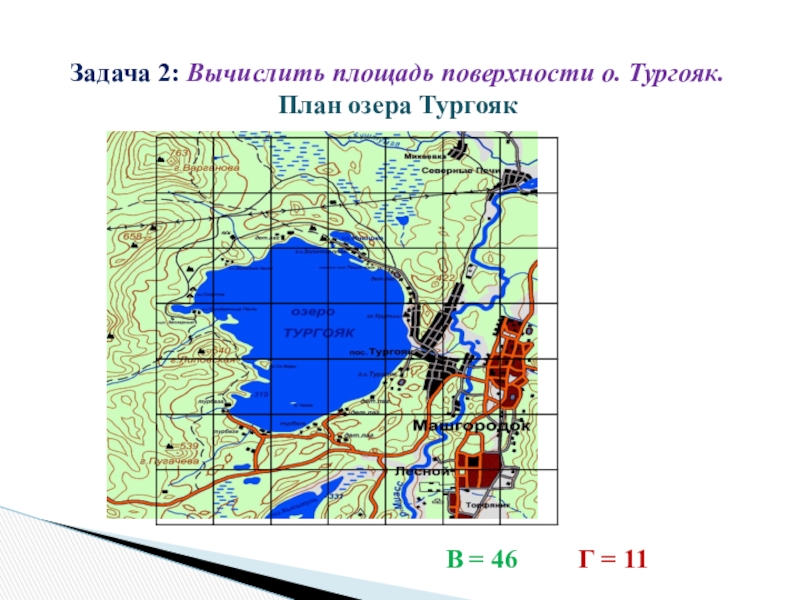
- 34. Задача 2: Вычислить площадь поверхности о. Тургояк.
- 35. Решение:Масштаб 1: 50 000В = 46
- 36. ЗаключениеФормула Пика даёт быстрое и простое
- 37. Слайд 37
"Геометрия - есть знание величин, фигур и их границ, а также отношений между ними и производимых над ними операций, разнообразных положений и движений"Диа́дох Прокл
Слайд 1Одна формула за всех … формула Пика
Слайд 2"Геометрия - есть знание величин,
фигур и их границ, а также
отношений между ними
и производимых над ними операций,
разнообразных положений и движений"
Диа́дох Прокл
и производимых над ними операций,
разнообразных положений и движений"
Диа́дох Прокл
Слайд 3
Актуальность:
при решении задач по математике и геометрии часто встречаются задачи,
где нужно вычислить площадь фигур.
Если фигура сложная, то её площадь находить довольно долго.
Тема нашего проекта актуальна, потому что формула Пика значительно облегчит нахождение площадей различных геометрических фигур.
Если фигура сложная, то её площадь находить довольно долго.
Тема нашего проекта актуальна, потому что формула Пика значительно облегчит нахождение площадей различных геометрических фигур.
Введение
Слайд 4Гипотеза:
мы считаем, что вычисление площадей сложных фигур с помощью формулы Пика
легче, чем вычисление методом достраивания и разбивания фигур на части.
Слайд 5 Объект исследования:
формула Пика для вычисления площадей многоугольников.
Предмет исследования:
применение формулы
Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге.
Цель:
обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.
Цель:
обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.
Слайд 6
Задачи:
1. Изучить методы вычисления площадей сложных фигур на
плоскости.
2. Научиться применять формулу Пика для вычисления площадей.
3. Сравнить и проанализировать результаты исследования.
4. Рекомендовать учащимся применять формулу Пика при решении задач ЕГЭ.
2. Научиться применять формулу Пика для вычисления площадей.
3. Сравнить и проанализировать результаты исследования.
4. Рекомендовать учащимся применять формулу Пика при решении задач ЕГЭ.
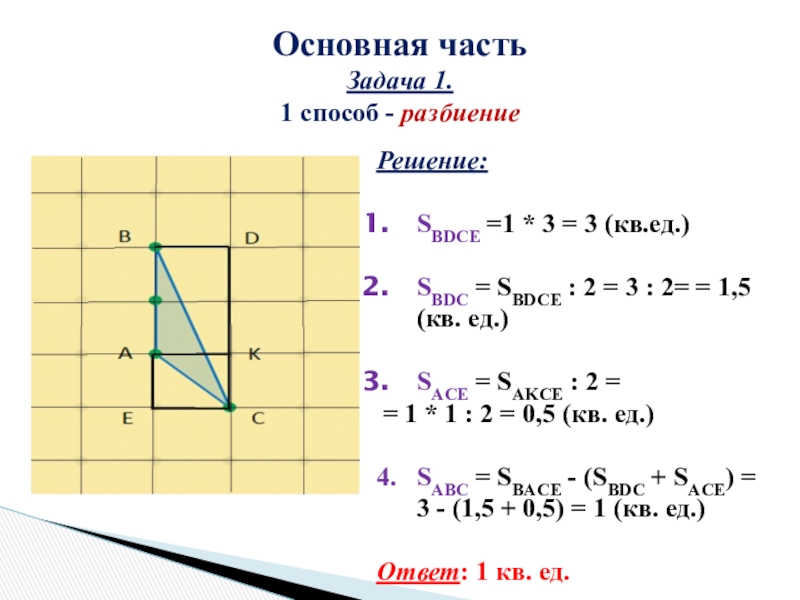
Слайд 8Основная часть
Задача 1.
1 способ - разбиение
Решение:
SBDCE =1 * 3 = 3
(кв.ед.)
SBDC = SBDCE : 2 = 3 : 2= = 1,5 (кв. ед.)
SACE = SAKCE : 2 =
= 1 * 1 : 2 = 0,5 (кв. ед.)
4. SABC = SBACE - (SBDC + SACE) = 3 - (1,5 + 0,5) = 1 (кв. ед.)
Ответ: 1 кв. ед.
SBDC = SBDCE : 2 = 3 : 2= = 1,5 (кв. ед.)
SACE = SAKCE : 2 =
= 1 * 1 : 2 = 0,5 (кв. ед.)
4. SABC = SBACE - (SBDC + SACE) = 3 - (1,5 + 0,5) = 1 (кв. ед.)
Ответ: 1 кв. ед.
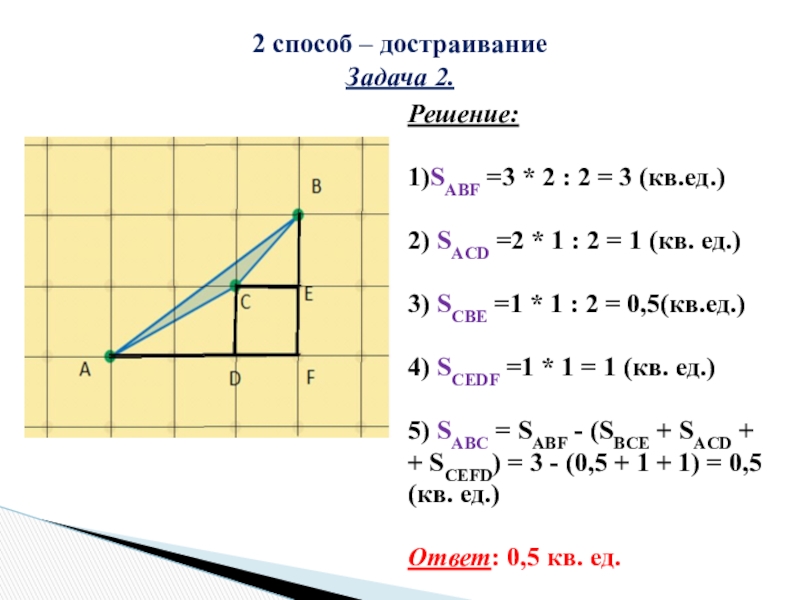
Слайд 92 способ – достраивание
Задача 2.
Решение:
1)SABF =3 * 2 : 2 =
3 (кв.ед.)
2) SACD =2 * 1 : 2 = 1 (кв. ед.)
3) SCBE =1 * 1 : 2 = 0,5(кв.ед.)
4) SCEDF =1 * 1 = 1 (кв. ед.)
5) SABC = SABF - (SBCE + SACD +
+ SCEFD) = 3 - (0,5 + 1 + 1) = 0,5 (кв. ед.)
Ответ: 0,5 кв. ед.
2) SACD =2 * 1 : 2 = 1 (кв. ед.)
3) SCBE =1 * 1 : 2 = 0,5(кв.ед.)
4) SCEDF =1 * 1 = 1 (кв. ед.)
5) SABC = SABF - (SBCE + SACD +
+ SCEFD) = 3 - (0,5 + 1 + 1) = 0,5 (кв. ед.)
Ответ: 0,5 кв. ед.
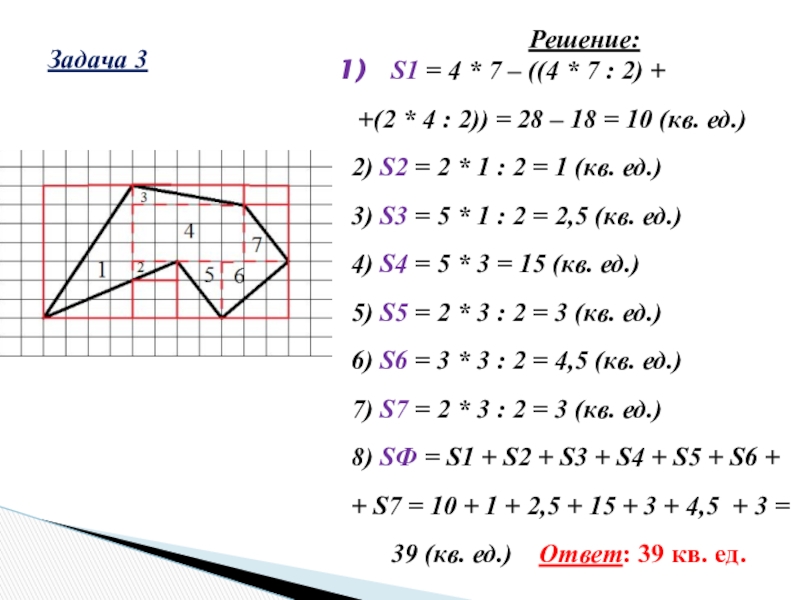
Слайд 10Задача 3
Решение:
S1 = 4 * 7 – ((4 * 7
: 2) +
+(2 * 4 : 2)) = 28 – 18 = 10 (кв. ед.)
2) S2 = 2 * 1 : 2 = 1 (кв. ед.)
3) S3 = 5 * 1 : 2 = 2,5 (кв. ед.)
4) S4 = 5 * 3 = 15 (кв. ед.)
5) S5 = 2 * 3 : 2 = 3 (кв. ед.)
6) S6 = 3 * 3 : 2 = 4,5 (кв. ед.)
7) S7 = 2 * 3 : 2 = 3 (кв. ед.)
8) SФ = S1 + S2 + S3 + S4 + S5 + S6 +
+ S7 = 10 + 1 + 2,5 + 15 + 3 + 4,5 + 3 = 39 (кв. ед.) Ответ: 39 кв. ед.
+(2 * 4 : 2)) = 28 – 18 = 10 (кв. ед.)
2) S2 = 2 * 1 : 2 = 1 (кв. ед.)
3) S3 = 5 * 1 : 2 = 2,5 (кв. ед.)
4) S4 = 5 * 3 = 15 (кв. ед.)
5) S5 = 2 * 3 : 2 = 3 (кв. ед.)
6) S6 = 3 * 3 : 2 = 4,5 (кв. ед.)
7) S7 = 2 * 3 : 2 = 3 (кв. ед.)
8) SФ = S1 + S2 + S3 + S4 + S5 + S6 +
+ S7 = 10 + 1 + 2,5 + 15 + 3 + 4,5 + 3 = 39 (кв. ед.) Ответ: 39 кв. ед.
Слайд 11 Вывод:
После решения этих задач мы поняли, что вычислять площади фигур
«достраиванием» или «разбиением» сложно и долго.
Есть другой способ для вычисления площади фигур на клетчатой бумаге, используя
Формулу Пика.
Есть другой способ для вычисления площади фигур на клетчатой бумаге, используя
Формулу Пика.
Слайд 12 Георг Александр Пик -
(10. 09.
1859 – 13. 07. 1942)
– австрийский математик.
Им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций,
теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. Широкую известность получила открытая им теорема Пика для расчёта площади многоугольника.
– австрийский математик.
Им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций,
теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. Широкую известность получила открытая им теорема Пика для расчёта площади многоугольника.
Создатель формулы
Слайд 13
В – внутренние узлы Г – граничные узлы
Алгоритм вычисления площади
многоугольника
с помощью формулы Пика:
1) Отметить внутренние и граничные узлы.
2) Считаем количество внутренних узлов, граничных узлов.
3) Находим площадь фигуры по формуле:
S = В + Г : 2 - 1.
с помощью формулы Пика:
1) Отметить внутренние и граничные узлы.
2) Считаем количество внутренних узлов, граничных узлов.
3) Находим площадь фигуры по формуле:
S = В + Г : 2 - 1.
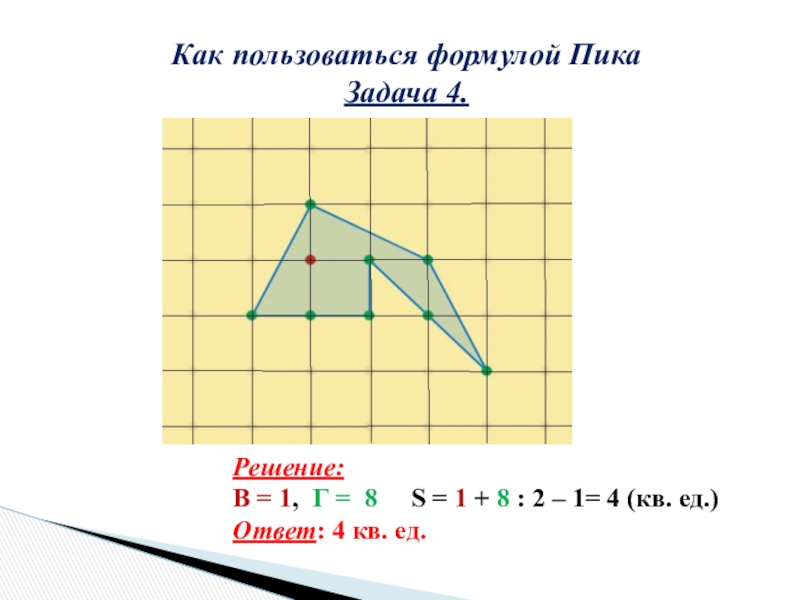
Слайд 14Как пользоваться формулой Пика
Задача 4.
Решение:
В = 1, Г = 8
S = 1 + 8 : 2 – 1= 4 (кв. ед.)
Ответ: 4 кв. ед.
Ответ: 4 кв. ед.
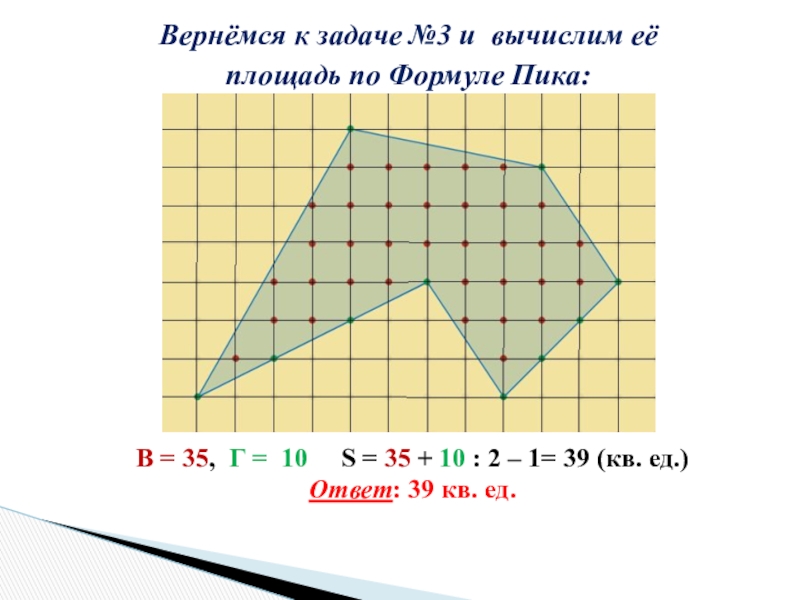
Слайд 15Вернёмся к задаче №3 и вычислим её
площадь по Формуле Пика:
В = 35,
Г = 10 S = 35 + 10 : 2 – 1= 39 (кв. ед.)
Ответ: 39 кв. ед.
Ответ: 39 кв. ед.
Слайд 20
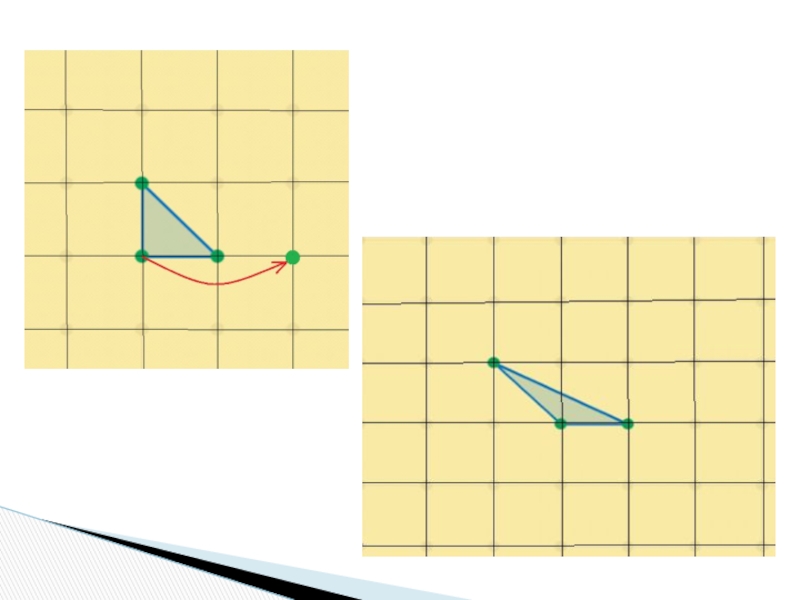
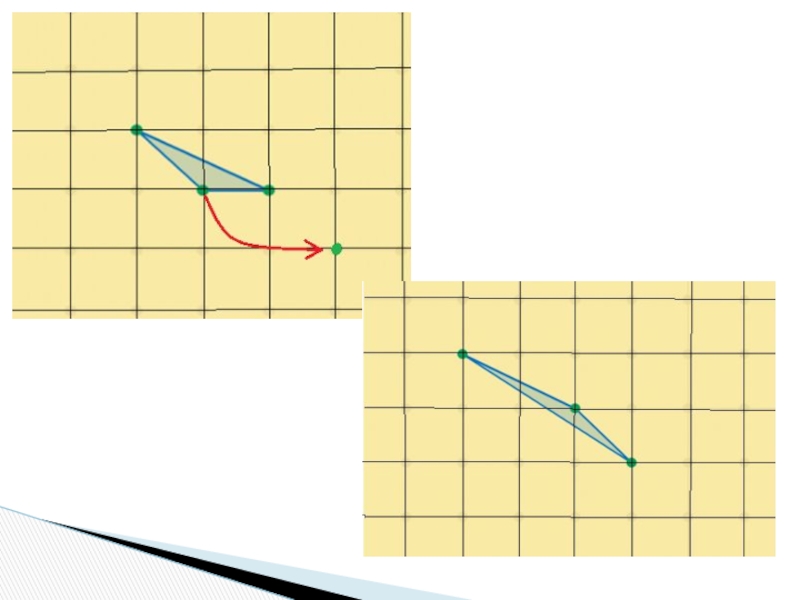
Вывод:
Площадь треугольника при прыжке одного кузнечика не меняется.
Любой простой треугольник
достижим.
Любой достижимый треугольник имеет площадь ½ кв. ед.
Из простого треугольника при прыжке получается простой.
Любой достижимый треугольник имеет площадь ½ кв. ед.
Из простого треугольника при прыжке получается простой.
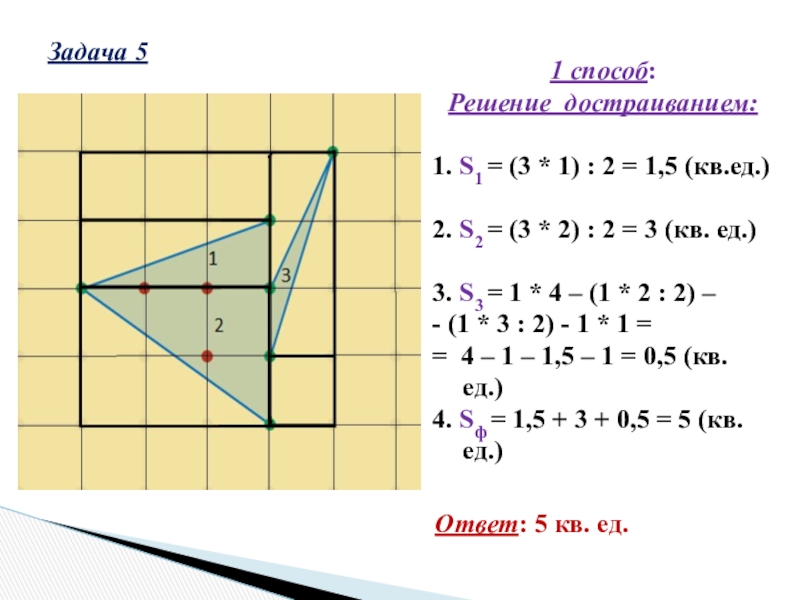
Слайд 22Задача 5
1 способ:
Решение достраиванием:
1. S1 = (3 * 1) : 2
= 1,5 (кв.ед.)
2. S2 = (3 * 2) : 2 = 3 (кв. ед.)
3. S3 = 1 * 4 – (1 * 2 : 2) –
- (1 * 3 : 2) - 1 * 1 =
= 4 – 1 – 1,5 – 1 = 0,5 (кв. ед.)
4. Sф = 1,5 + 3 + 0,5 = 5 (кв.ед.)
Ответ: 5 кв. ед.
2. S2 = (3 * 2) : 2 = 3 (кв. ед.)
3. S3 = 1 * 4 – (1 * 2 : 2) –
- (1 * 3 : 2) - 1 * 1 =
= 4 – 1 – 1,5 – 1 = 0,5 (кв. ед.)
4. Sф = 1,5 + 3 + 0,5 = 5 (кв.ед.)
Ответ: 5 кв. ед.
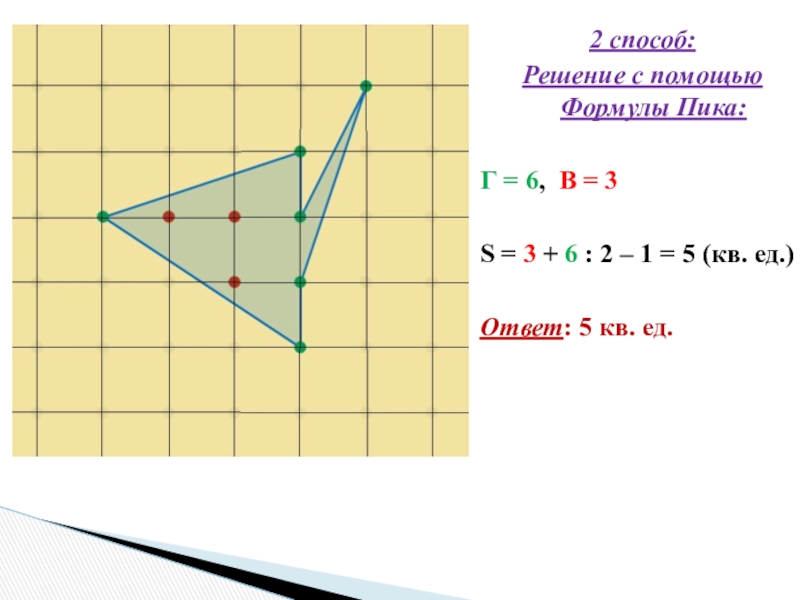
Слайд 232 способ:
Решение с помощью Формулы Пика:
Г = 6, В =
3
S = 3 + 6 : 2 – 1 = 5 (кв. ед.)
Ответ: 5 кв. ед.
S = 3 + 6 : 2 – 1 = 5 (кв. ед.)
Ответ: 5 кв. ед.
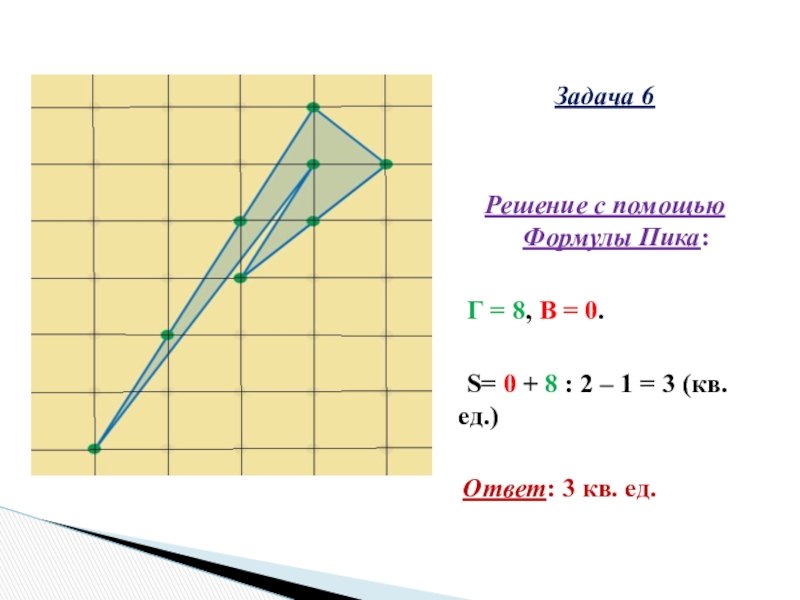
Слайд 24Задача 6
Решение с помощью Формулы Пика:
Г = 8, В = 0.
S=
0 + 8 : 2 – 1 = 3 (кв. ед.)
Ответ: 3 кв. ед.
Ответ: 3 кв. ед.
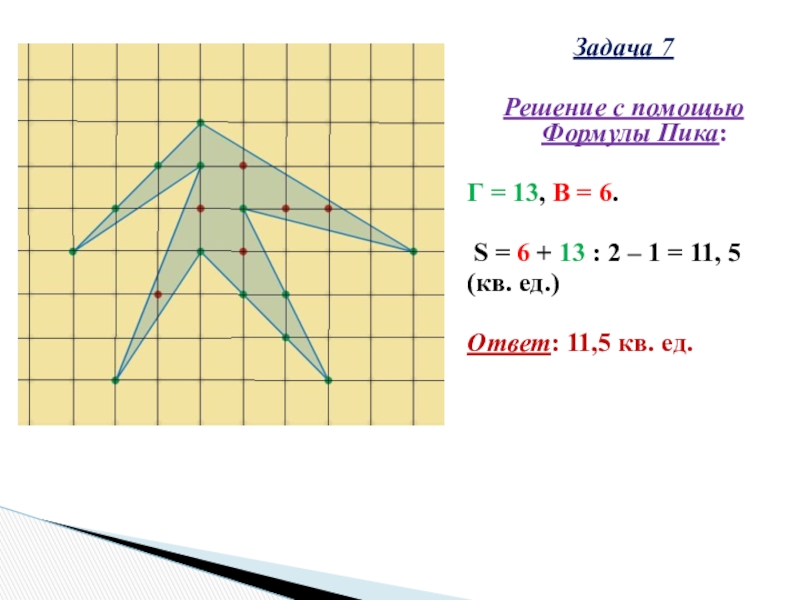
Слайд 25Задача 7
Решение с помощью Формулы Пика:
Г = 13, В = 6.
S
= 6 + 13 : 2 – 1 = 11, 5
(кв. ед.)
Ответ: 11,5 кв. ед.
(кв. ед.)
Ответ: 11,5 кв. ед.
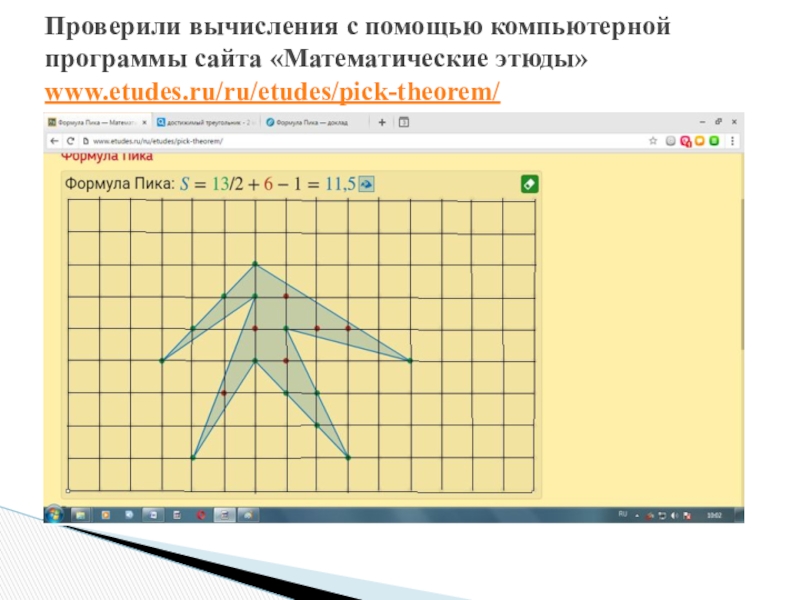
Слайд 26
Проверили вычисления с помощью компьютерной программы сайта «Математические этюды» www.etudes.ru/ru/etudes/pick-theorem/
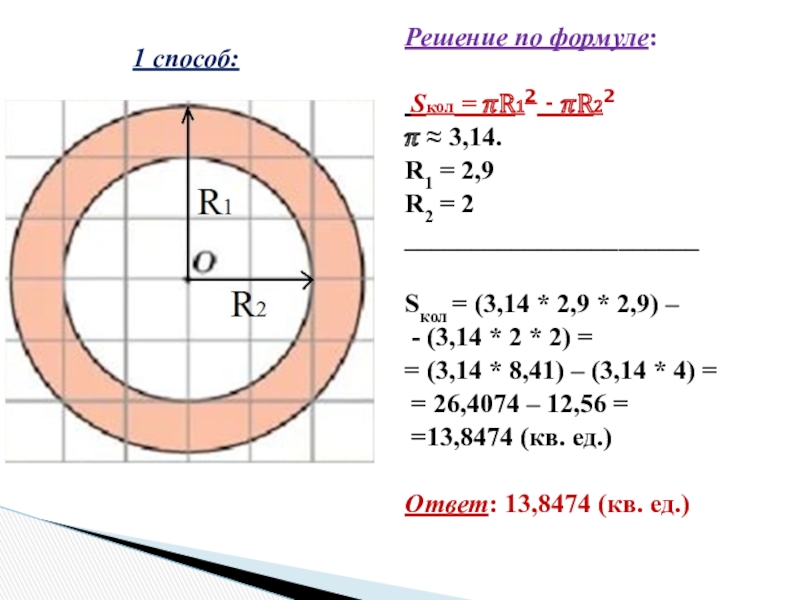
Слайд 28Решение по формуле:
Sкол = ?R12 - ?R22
? ≈ 3,14.
R1
= 2,9
R2 = 2
______________________
Sкол = (3,14 * 2,9 * 2,9) –
- (3,14 * 2 * 2) =
= (3,14 * 8,41) – (3,14 * 4) =
= 26,4074 – 12,56 =
=13,8474 (кв. ед.)
Ответ: 13,8474 (кв. ед.)
R2 = 2
______________________
Sкол = (3,14 * 2,9 * 2,9) –
- (3,14 * 2 * 2) =
= (3,14 * 8,41) – (3,14 * 4) =
= 26,4074 – 12,56 =
=13,8474 (кв. ед.)
Ответ: 13,8474 (кв. ед.)
1 способ:
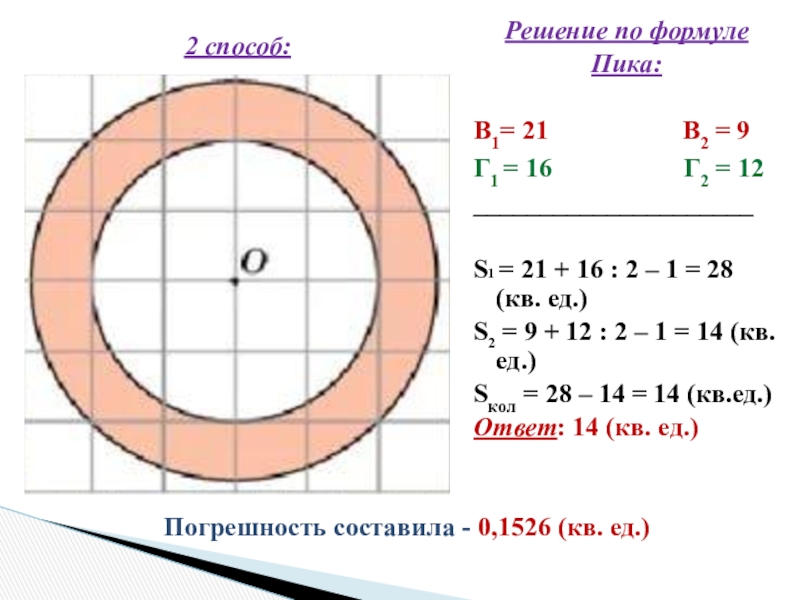
Слайд 29Решение по формуле
Пика:
В1= 21
В2 = 9
Г1 = 16 Г2 = 12
_____________________
S1 = 21 + 16 : 2 – 1 = 28 (кв. ед.)
S2 = 9 + 12 : 2 – 1 = 14 (кв. ед.)
Sкол = 28 – 14 = 14 (кв.ед.)
Ответ: 14 (кв. ед.)
Г1 = 16 Г2 = 12
_____________________
S1 = 21 + 16 : 2 – 1 = 28 (кв. ед.)
S2 = 9 + 12 : 2 – 1 = 14 (кв. ед.)
Sкол = 28 – 14 = 14 (кв.ед.)
Ответ: 14 (кв. ед.)
2 способ:
Погрешность составила - 0,1526 (кв. ед.)
Слайд 33Масштаб 1 : 400
1 см2 = 16 м2
1) Находим
площадь одного этажа школы:
99 + 62 : 2 – 1 = 129 см2
129 см2 = 129 * 16 = 2064 м2
2) Находим общую площадь школы:
2064 * 3 = 6192 м2
Наш результат – 6192 м2.
Настоящая площадь – 6222 м2
Погрешность составила - 30 м2
99 + 62 : 2 – 1 = 129 см2
129 см2 = 129 * 16 = 2064 м2
2) Находим общую площадь школы:
2064 * 3 = 6192 м2
Наш результат – 6192 м2.
Настоящая площадь – 6222 м2
Погрешность составила - 30 м2
Решение:
Слайд 35Решение:
Масштаб 1: 50 000
В = 46 Г =
11
S = 46 + 11 : 2 - 1 = 51,5 (кв. ед.)
51,5 * 50000 = 2575000 см2 = 25,75 км2
Ответ: 25,75 км2
Площадь о. Тургояк – 26,4 км2
Погрешность составила 0,65 км2
S = 46 + 11 : 2 - 1 = 51,5 (кв. ед.)
51,5 * 50000 = 2575000 см2 = 25,75 км2
Ответ: 25,75 км2
Площадь о. Тургояк – 26,4 км2
Погрешность составила 0,65 км2
Слайд 36
Заключение
Формула Пика даёт быстрое и простое решение задач на нахождение
площади фигуры на клетчатой бумаге, вершины которой лежат в узлах решётки, то есть нахождения площадей многоугольников.
Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.
Формула Пика не применяется для решения задач в пространстве.
Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.
Формула Пика не применяется для решения задач в пространстве.