признаки прямоугольника.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Гл. 1. Урок 10. Ромб и квадрат.
Содержание
- 1. Презентация. Гл. 1. Урок 10. Ромб и квадрат.
- 2. Задача № 404Решение: пусть ВО – медиана
- 3. Задача 1 Дано:АВСD – прямоугольник. АК
- 4. Задача 2 Дано:АВСD – прямоугольникﮮ CАD
- 5. Задача 3Дано: ABCD – прямоугольник,BD =12 см,
- 6. Квадрат
- 7. Что мы знаем о квадрате?1. Изображение2. ОбозначениеАВСD3. Все углы прямые4. Все стороны равны5. Р = 4∙а
- 8. КвадратЧем квадрат отличается от прямоугольника?
- 9. Определение:Квадрат – это прямоугольник, у которого все
- 10. Свойства квадратаВсе стороны квадрата равны и все
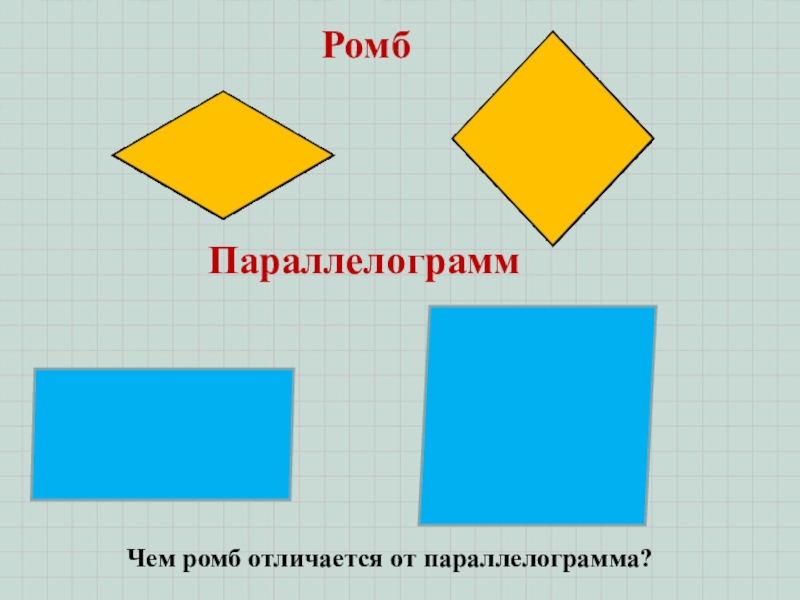
- 11. РомбЧем ромб отличается от параллелограмма?Параллелограмм
- 12. Определение: ромб – параллелограмм, у которого все
- 13. Доказательство1. AB=AD (по определению ромба)Дано: ABCD –
- 14. Слайд 14
- 15. К основным свойствам квадрата добавляется еще одно:
- 16. Домашнее заданиеЧитать п. 47;Учить доказательство свойств диагоналей
Задача № 404Решение: пусть ВО – медиана прямоугольного треугольника АВС. Построим точку D, симметричную точке В относительно точки О и четырехугольник ABCD.ВО = OD (по построению), АО = ОС (по условию) , значит четырехугольник АВСD –параллелограмм
Слайд 1
Вопросы для устного повторения
Дайте определение прямоугольника.
Перечислите свойства прямоугольника.
Докажите одно из них.
Перечислите
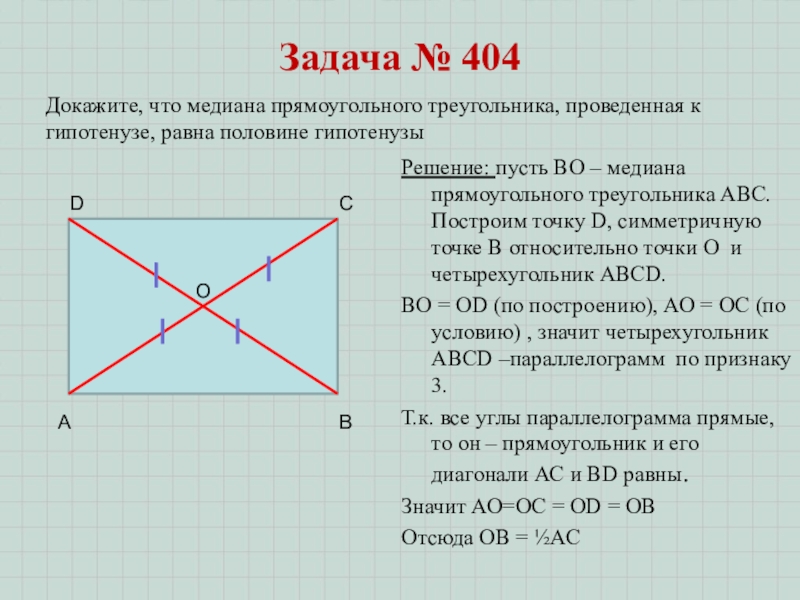
Слайд 2Задача № 404
Решение: пусть ВО – медиана прямоугольного треугольника АВС. Построим
точку D, симметричную точке В относительно точки О и четырехугольник ABCD.
ВО = OD (по построению), АО = ОС (по условию) , значит четырехугольник АВСD –параллелограмм по признаку 3.
Т.к. все углы параллелограмма прямые, то он – прямоугольник и его диагонали АС и BD равны.
Значит АО=ОС = ОD = ОВ
Отсюда ОВ = ½АС
ВО = OD (по построению), АО = ОС (по условию) , значит четырехугольник АВСD –параллелограмм по признаку 3.
Т.к. все углы параллелограмма прямые, то он – прямоугольник и его диагонали АС и BD равны.
Значит АО=ОС = ОD = ОВ
Отсюда ОВ = ½АС
D
C
B
A
O
Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы
Слайд 3
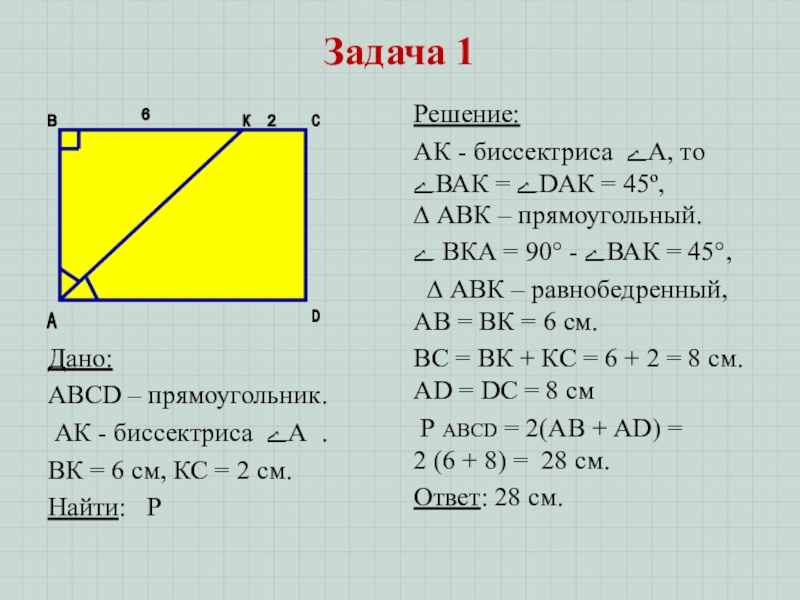
Задача 1
Дано:
АВСD – прямоугольник.
АК - биссектриса ﮮА .
ВК = 6
см, КС = 2 см.
Найти: Р
Найти: Р
А
В
К
D
С
6
2
АВСD
Решение:
АК - биссектриса ﮮА, то ﮮВАК = ﮮDАК = 45º, ∆ АВК – прямоугольный.
ﮮ ВКА = 90° - ﮮВАК = 45°,
∆ АВК – равнобедренный, АВ = ВК = 6 см.
ВС = ВК + КС = 6 + 2 = 8 см. АD = DC = 8 cм
Р АВСD = 2(АВ + АD) = 2 (6 + 8) = 28 см.
Ответ: 28 см.
Слайд 4
Задача 2
Дано:
АВСD – прямоугольник
ﮮ CАD = 30º .
АС =
14 см.
Найти: Р ∆ АОВ
Найти: Р ∆ АОВ
А
В
D
С
30
О
Решение:
∆ АСD – прямоугольный, в нём < САD = 30º , значит СD =АС/2 = 7см.
Тогда АВ = СD = 7 см.
В прямоугольнике диагонали равны и точкой пересечения делятся пополам,
АО = АС/2 = ВD/2 = ВО = 7 см. Р ∆ АОВ = АО + ВО + АВ = 21 см. Ответ: 21 см.
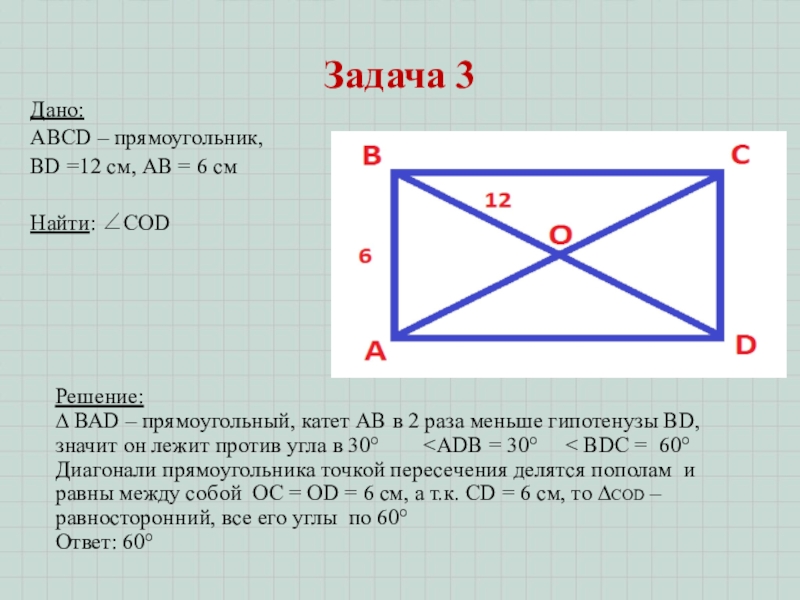
Слайд 5Задача 3
Дано:
ABCD – прямоугольник,
BD =12 см, AB = 6 см
Найти:
∠COD
Решение:
∆ ВАD – прямоугольный, катет АВ в 2 раза меньше гипотенузы BD, значит он лежит против угла в 30° <АDB = 30° < BDC = 60°
Диагонали прямоугольника точкой пересечения делятся пополам и равны между собой ОС = ОD = 6 cм, а т.к. CD = 6 cм, то ∆СОD –равносторонний, все его углы по 60°
Ответ: 60°
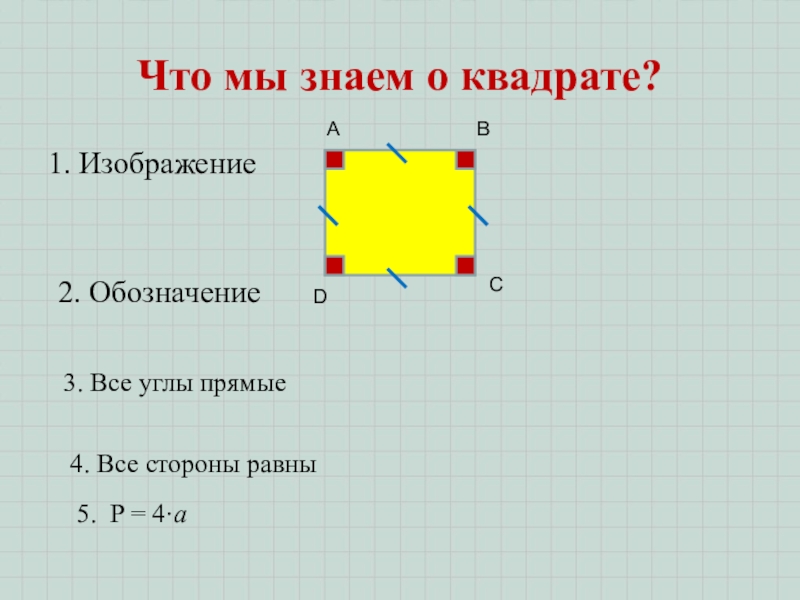
Слайд 7Что мы знаем о квадрате?
1. Изображение
2. Обозначение
А
В
С
D
3. Все углы прямые
4. Все
стороны равны
5. Р = 4∙а
Слайд 9Определение:
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник является параллелограммом,
поэтому и квадрат является параллелограммом
Квадрат обладает всеми свойствами
параллелограмма и прямоугольника
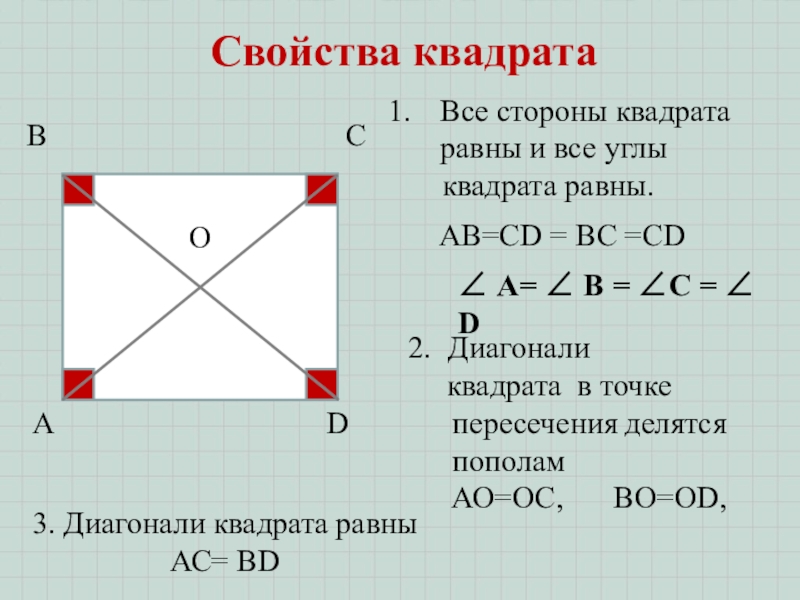
Слайд 10Свойства квадрата
Все стороны квадрата равны и все углы
квадрата
равны.
2. Диагонали
квадрата в точке пересечения делятся пополам
АО=ОС,
∠ А= ∠ В = ∠C = ∠ D
ВО=ОD,
АB=СD = ВС =CD
3. Диагонали квадрата равны
АС= BD
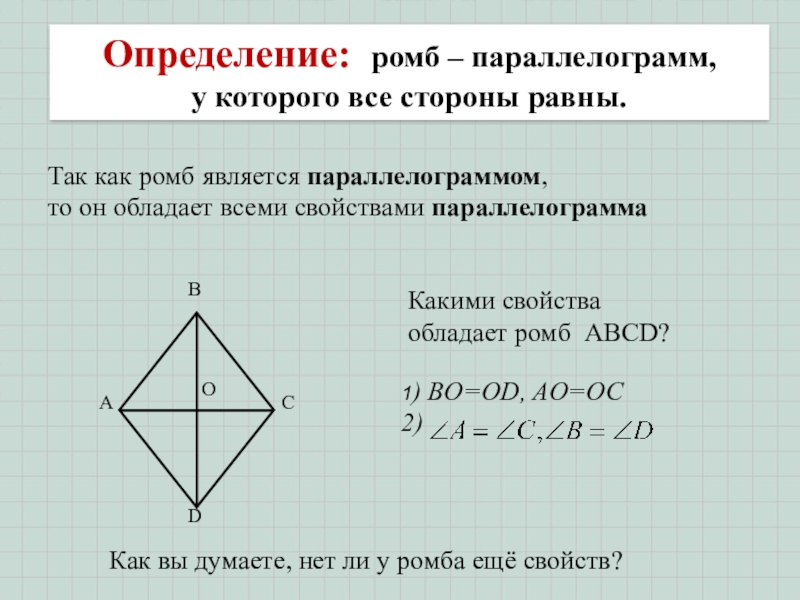
Слайд 12Определение: ромб – параллелограмм,
у которого все стороны равны.
Так как ромб
является параллелограммом,
то он обладает всеми свойствами параллелограмма
то он обладает всеми свойствами параллелограмма
A
B
C
D
O
Какими свойства
обладает ромб ABCD?
Как вы думаете, нет ли у ромба ещё свойств?
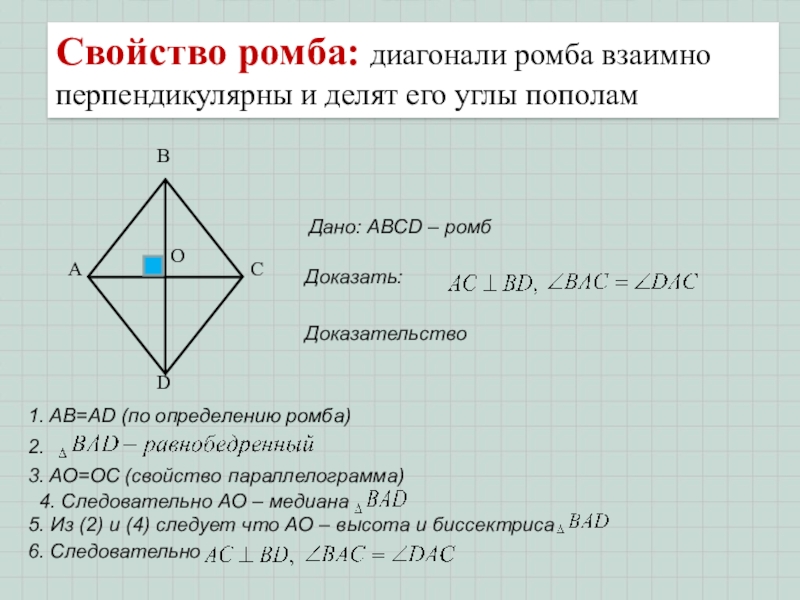
Слайд 13Доказательство
1. AB=AD (по определению ромба)
Дано: ABCD – ромб
A
B
C
D
O
3. AO=OC (свойство параллелограмма)
Свойство
ромба: диагонали ромба взаимно перпендикулярны и делят его углы пополам
Слайд 15К основным свойствам квадрата добавляется еще одно:
Диагонали квадрата равны, взаимно
перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам
Слайд 16Домашнее задание
Читать п. 47;
Учить доказательство свойств диагоналей ромба и квадрата;
Сформулировать и
записать теорему, выражающую собой признак ромба (обратную терему).
Решить №№ 412, 413
Решить №№ 412, 413
