- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение сечений многогранников (презентация) (10 класс)
Содержание
- 1. Построение сечений многогранников (презентация) (10 класс)
- 2. Содержание1.Построение точки пересечения прямой с плоскостью1.Построение точки
- 3. Построение точки пересечения прямой с плоскостью Построение
- 4. Построение точки пересечения прямой с плоскостью Пример
- 5. Построение точки пересечения прямой с плоскостьюПример 3.
- 6. Построение точки пересечения прямой с плоскостьюПример 4.
- 7. Построение точки пересечения прямой с плоскостьюПример 5.
- 8. Пример 6. Построить точку пересечения прямой
- 9. Пример 7. В прямой призме ABCDA'B'C'D'
- 10. Пример 8. Дан параллелепипед ABCDA'B'C'D' , M
- 11. Пример 9. Точка М лежит на ребре
- 12. Пример 10. М – точка на
- 13. в) плоскости ВDD‘ Построение.К'К | | ВВ'
- 14. Пример 11. Постройте сечение тетраэдра SABC,
- 15. Пример 12. Построить сечение тетраэдра плоскостью
- 16. Пример 13 Постройте сечение параллелепипеда АВСDA'B'C'D' плоскостями,
- 17. Построение сечений многогранников методом следов Сечение выпуклого
- 18. Пример 14. На ребрах АВ, BD
- 19. Задача 15. На ребрах АА', А'D'
- 20. Пример 16. Даны точки М и
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Используемые литература и программное обеспечениеА.В Погорелов
Содержание1.Построение точки пересечения прямой с плоскостью1.Построение точки пересечения прямой с плоскостью.2.Задачи на построение точки пересечения прямой и плоскости2.Задачи на построение точки пересечения прямой и плоскости.3. Построение сечения, параллельного данной прямой или данной3. Построение сечения, параллельного данной
Слайд 2Содержание
1.Построение точки пересечения прямой с плоскостью1.Построение точки пересечения прямой с плоскостью.
2.Задачи
на построение точки пересечения прямой и плоскости2.Задачи на построение точки пересечения прямой и плоскости.
3. Построение сечения, параллельного данной прямой или данной3. Построение сечения, параллельного данной прямой или данной 3. Построение сечения, параллельного данной прямой или данной плоскости.
4.Задачи на построение сечения, параллельного данной прямой или данной плоскости.
5. Построение сечений многогранников методом следов
6. Задачи на построение сечений многогранников методом следов
7. Используемые литература и программные обеспечения
3. Построение сечения, параллельного данной прямой или данной3. Построение сечения, параллельного данной прямой или данной 3. Построение сечения, параллельного данной прямой или данной плоскости.
4.Задачи на построение сечения, параллельного данной прямой или данной плоскости.
5. Построение сечений многогранников методом следов
6. Задачи на построение сечений многогранников методом следов
7. Используемые литература и программные обеспечения
Слайд 3Построение точки пересечения прямой с плоскостью
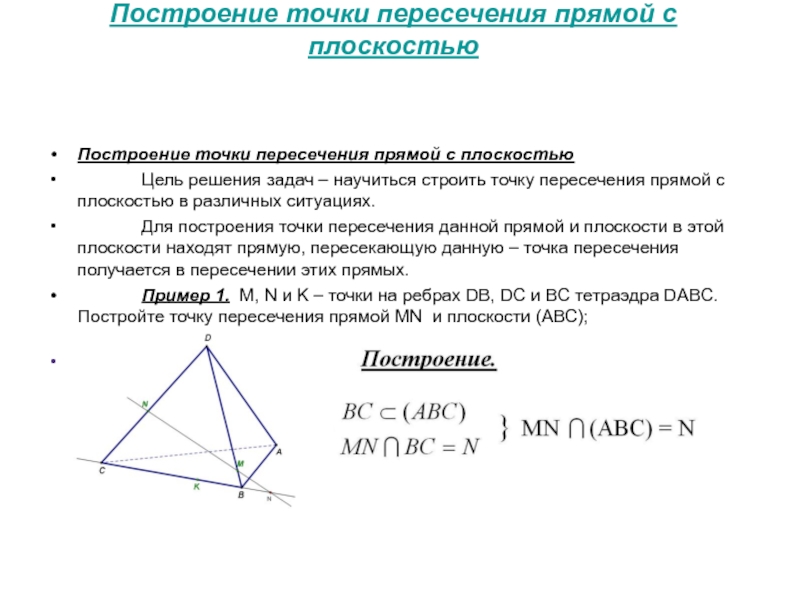
Построение точки пересечения прямой с плоскостью
Цель решения задач – научиться строить точку пересечения прямой с плоскостью в различных ситуациях.
Для построения точки пересечения данной прямой и плоскости в этой плоскости находят прямую, пересекающую данную – точка пересечения получается в пересечении этих прямых.
Пример 1. M, N и K – точки на ребрах DB, DC и BC тетраэдра DABC. Постройте точку пересечения прямой MN и плоскости (АВС);
Для построения точки пересечения данной прямой и плоскости в этой плоскости находят прямую, пересекающую данную – точка пересечения получается в пересечении этих прямых.
Пример 1. M, N и K – точки на ребрах DB, DC и BC тетраэдра DABC. Постройте точку пересечения прямой MN и плоскости (АВС);
Слайд 4Построение точки пересечения прямой с плоскостью
Пример 2. M и N
– точки на ребрах ВВ' и СС' параллелепипеда ABCDA'B'C'D'. Постройте точку пересечения прямой MN и плоскости (АВС):
Слайд 5Построение точки пересечения прямой с плоскостью
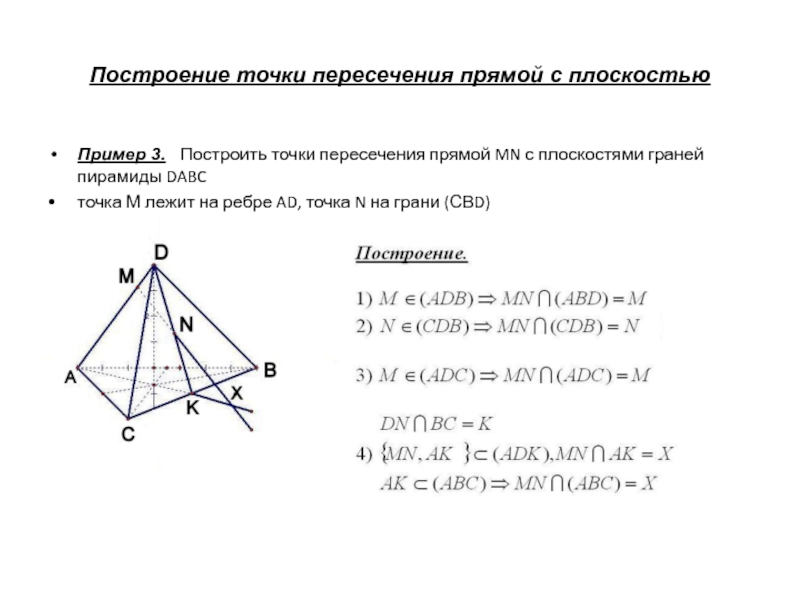
Пример 3. Построить точки пересечения
прямой MN с плоскостями граней пирамиды DABC
точка М лежит на ребре AD, точка N на грани (СВD)
а)
точка М лежит на ребре AD, точка N на грани (СВD)
а)
Слайд 6Построение точки пересечения прямой с плоскостью
Пример 4. Построить точку пересечения прямой
MN с плоскостью грани АВС пирамиды DABC, если точка М лежит на грани (ADC) , N – на грани (BCD).
Слайд 7Построение точки пересечения прямой с плоскостью
Пример 5. Построить точку
пересечения прямой MN с плоскостью грани ABD пирамиды DABC, если точка М лежит на грани (ADC) , N – на грани BCD.
Построение:
Построение:
Слайд 8
Пример 6. Построить точку пересечения прямой MN с плоскостью грани
ABCD призмы ABCDA'B'C'D'.М принадлежит ребру А'В', N – ребру DD'.
Построение:
Построение:
Слайд 9
Пример 7. В прямой призме ABCDA'B'C'D' точка М лежит на
грани АА'В'В, а точка N – на грани СС'D'D. Постройте точку пересечения прямой MN с плоскостью нижнего основания.
Построение:
Построение:
Слайд 10
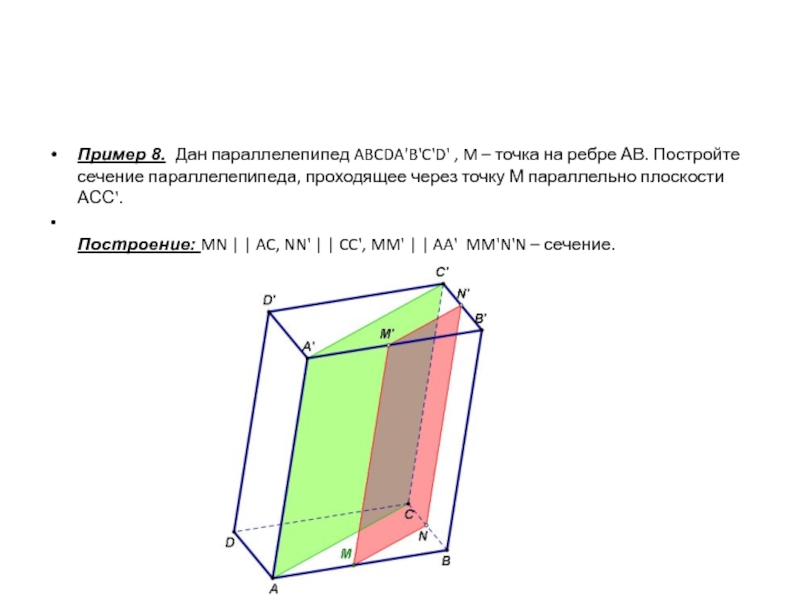
Пример 8. Дан параллелепипед ABCDA'B'C'D' , M – точка на ребре
АВ. Постройте сечение параллелепипеда, проходящее через точку М параллельно плоскости АСС'.
Построение: MN | | AC, NN' | | CC', MM' | | AA' MM'N'N – сечение.
Построение: MN | | AC, NN' | | CC', MM' | | AA' MM'N'N – сечение.
Слайд 11
Пример 9. Точка М лежит на ребре ВС параллелепипеда ABCDA'B'C'D'. Постройте
сечение параллелепипеда плоскостью, проходящей через точку М параллельно плоскости ВDC'.
Построение: MM' | | BD, M'M'' | | DC' MM'M'' – сечение.
Построение: MM' | | BD, M'M'' | | DC' MM'M'' – сечение.
Слайд 12
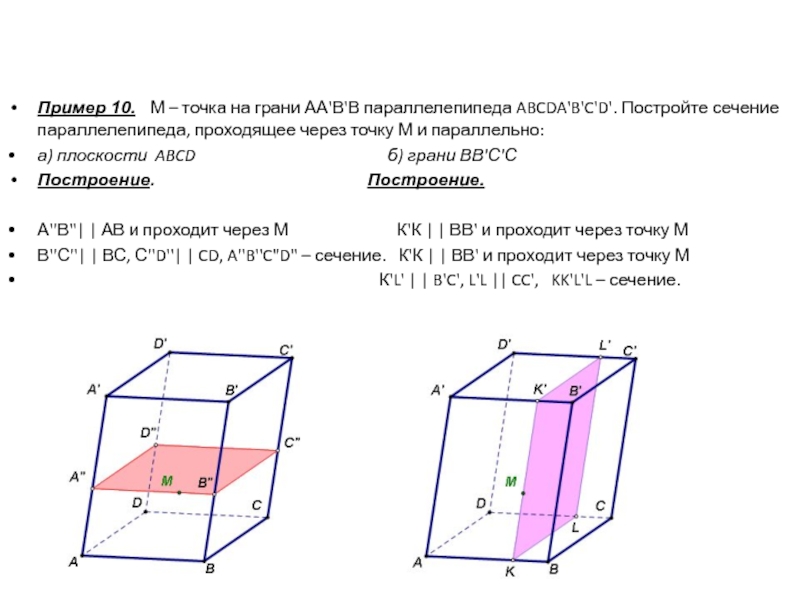
Пример 10. М – точка на грани АА'В'В параллелепипеда ABCDA'B'C'D'.
Постройте сечение параллелепипеда, проходящее через точку М и параллельно:
а) плоскости ABCD б) грани ВВ'С'С
Построение. Построение.
А''В''| | АВ и проходит через М К'К | | ВВ' и проходит через точку М
В''С''| | ВС, С''D''| | CD, A''B''C"D" – сечение. К'К | | ВВ' и проходит через точку М
К'L' | | B'C', L'L || CC', KK'L'L – сечение.
а) плоскости ABCD б) грани ВВ'С'С
Построение. Построение.
А''В''| | АВ и проходит через М К'К | | ВВ' и проходит через точку М
В''С''| | ВС, С''D''| | CD, A''B''C"D" – сечение. К'К | | ВВ' и проходит через точку М
К'L' | | B'C', L'L || CC', KK'L'L – сечение.
Слайд 13
в) плоскости ВDD‘
Построение.
К'К | | ВВ' и проходит через точку
М
K'N' | | B'D', KN| | BD, KK'N'N – сечение.
K'N' | | B'D', KN| | BD, KK'N'N – сечение.
Слайд 14
Пример 11. Постройте сечение тетраэдра SABC, проходящее через середины ребер
АВ и ВС параллельно ребру SB. Докажите, что оно пересекает грани SAB и SBC по параллельным прямым.
Построение: LL'| | SB, KK'| | SB, LL'K'K – сечение.
Построение: LL'| | SB, KK'| | SB, LL'K'K – сечение.
Слайд 15
Пример 12. Построить сечение тетраэдра плоскостью DABC плоскостью, параллельной АВС
и проходящей через точку
а) М – середину АD б) N – точку внутри грани ABD
Построение. Построение.
MB'| | BA, MC'| | AC, MB'C' – сечение. В"А"| | ВА и проходит через N
B"C"| | BC, A"B"C" – сечение.
а) М – середину АD б) N – точку внутри грани ABD
Построение. Построение.
MB'| | BA, MC'| | AC, MB'C' – сечение. В"А"| | ВА и проходит через N
B"C"| | BC, A"B"C" – сечение.
Слайд 16
Пример 13 Постройте сечение параллелепипеда АВСDA'B'C'D' плоскостями, проходящими через:
а) ребро СС'
и точку М пересечения б) точку N пересечения диагоналей грани ABCD
диагоналей грани АА'D'D параллельно плоскости АВ'С'
Построение Построение
М'М"| | D'D (CC'), M"C, M'C, Плоскость АВ'С'С, KL| | AD, KK'| | AB', LL'| | DC',
CM'M"C' – сечение. KK'L'L – сечение.
диагоналей грани АА'D'D параллельно плоскости АВ'С'
Построение Построение
М'М"| | D'D (CC'), M"C, M'C, Плоскость АВ'С'С, KL| | AD, KK'| | AB', LL'| | DC',
CM'M"C' – сечение. KK'L'L – сечение.
Слайд 17Построение сечений многогранников методом следов
Сечение выпуклого многогранника – выпуклый плоский
многоугольник , вершины которого являются точками пересечения секущей плоскости с ребрами многогранника, а стороны – с его гранями.
Для построения сечения нужно найти прямые, по которым плоскость сечения пересекается с плоскостями граней многогранника. Чтобы построить такие прямые находят для каждой из них две точки, через них и проводят прямую пересечения. Построение таких точек рассмотрено в §1.
Прямые пересечения секущей плоскости с плоскостями граней на чертеже называются следами секущей плоскости на плоскостях граней, отсюда и название метода.
В следующих задачах рассмотрю задачи, в которых точки, задающие секущую плоскость, принадлежат ребрам многогранника.
Для построения сечения нужно найти прямые, по которым плоскость сечения пересекается с плоскостями граней многогранника. Чтобы построить такие прямые находят для каждой из них две точки, через них и проводят прямую пересечения. Построение таких точек рассмотрено в §1.
Прямые пересечения секущей плоскости с плоскостями граней на чертеже называются следами секущей плоскости на плоскостях граней, отсюда и название метода.
В следующих задачах рассмотрю задачи, в которых точки, задающие секущую плоскость, принадлежат ребрам многогранника.
Слайд 18
Пример 14. На ребрах АВ, BD и CD тетраэдра ABCD
отмечены точки М, N и Р. Построить сечение тетраэдра плоскостью MNP.
Возможны два случая.
1 случай 2 случай
Построение: Построение:
PNAC = O, MOAB = K, PN| | AC, QM| | NP,
KPNM – сечение. QPNM – сечение.
Возможны два случая.
1 случай 2 случай
Построение: Построение:
PNAC = O, MOAB = K, PN| | AC, QM| | NP,
KPNM – сечение. QPNM – сечение.
Слайд 19
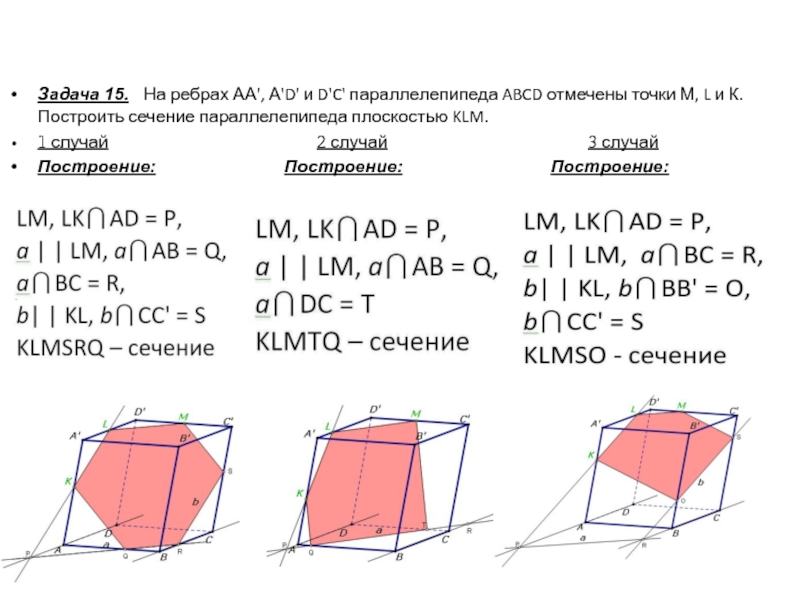
Задача 15. На ребрах АА', А'D' и D'C' параллелепипеда ABCD
отмечены точки М, L и К. Построить сечение параллелепипеда плоскостью KLM.
1 случай 2 случай 3 случай
Построение: Построение: Построение:
1 случай 2 случай 3 случай
Построение: Построение: Построение:
Слайд 20
Пример 16. Даны точки М и N на ребрах BD
и CD тетраэдра ABCD и точка К на грани АВС. Постройте сечение тетраэдра плоскостью MNK.
Построение:
Построение:
Пример 17. Даны точка К на ребре DC тетраэдра ABCD и точки М и N на гранях АВС и АСD.
Постройте сечение тетраэдра плоскостью MNK.
Построение:
Слайд 24Используемые литература и программное обеспечение
А.В Погорелов «Геометрия 10-11»
Л.С Атанасян
«Геометрия 10-11»
С.М. Саакян, А.М. Гольдман и др.«Математика»
Г. Дорофеев, М.Потапов «Математика для поступающих в вузы»
А. Д. Ботвинников и др. «Черчение»
Б.И. Аргунов, М. Б. Балк «Элементарная геометрия»
Программы: Adobe Photoshop
Компас-3D LT V9
«Живая геометрия»
PowerPoint
С.М. Саакян, А.М. Гольдман и др.«Математика»
Г. Дорофеев, М.Потапов «Математика для поступающих в вузы»
А. Д. Ботвинников и др. «Черчение»
Б.И. Аргунов, М. Б. Балк «Элементарная геометрия»
Программы: Adobe Photoshop
Компас-3D LT V9
«Живая геометрия»
PowerPoint