- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Игровой урок по теме: Теорема Пифагора
Содержание
- 1. Игровой урок по теме: Теорема Пифагора
- 2. «Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…»
- 3. История о Пифагоре:Пифагор родился в 580 г.
- 4. История теоремы: Изучение вавилонских
- 5. Теорему называли «мостом ослов», так как слабые
- 6. Команды:
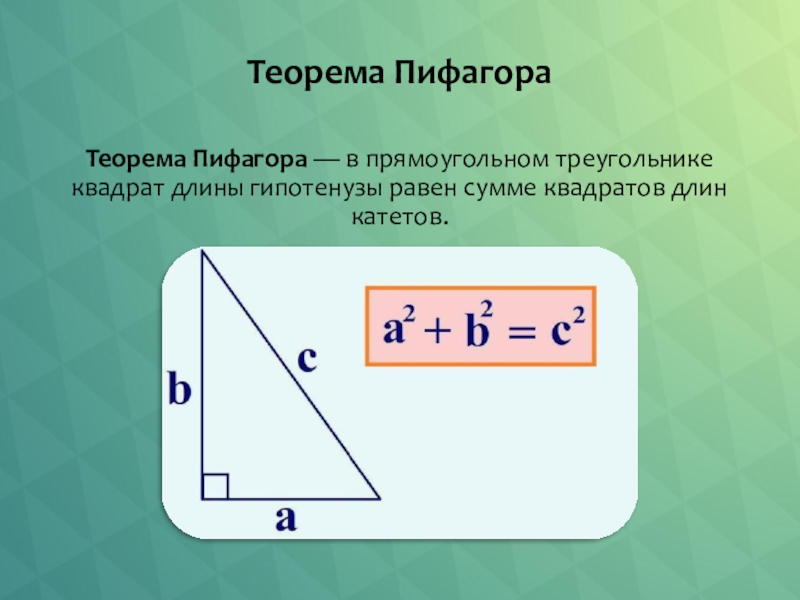
- 7. Теорема Пифагора Теорема Пифагора — в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
- 8. Задания для команд: 1 этап разминочный1 ряд2 ряд3 рядОценивается в 1 балл
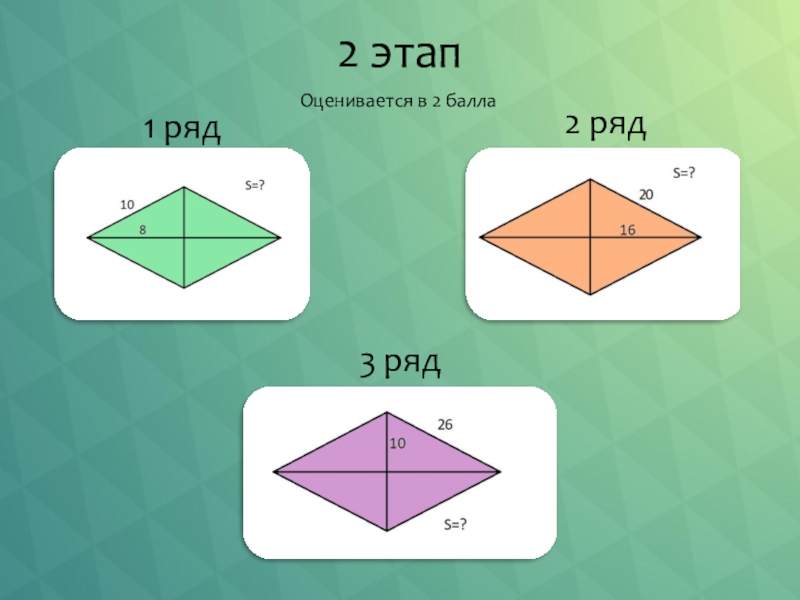
- 9. 2 этап1 ряд2 ряд3 рядОценивается в 2 балла
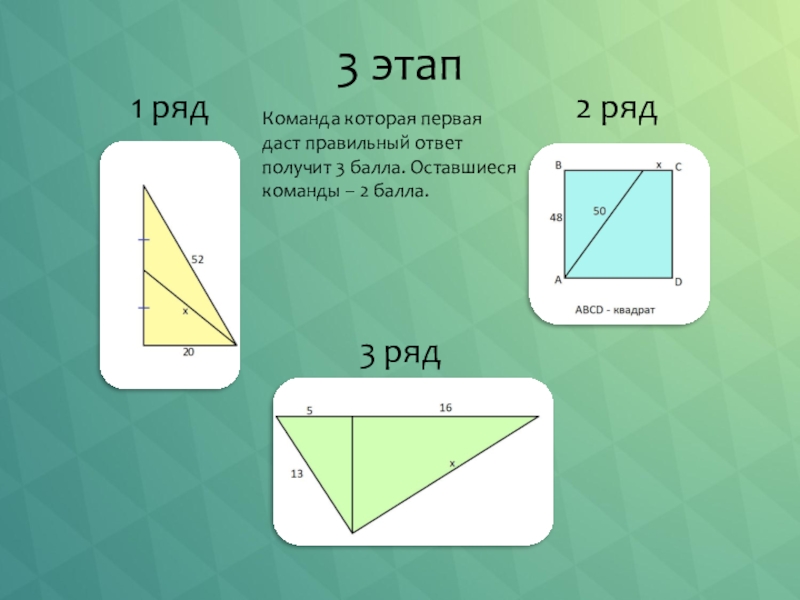
- 10. 3 этап1 ряд3 ряд2 рядКоманда которая первая
- 11. 4 этап задачи для капитанов1 ряд2 ряд3
- 12. На следующем слайде будет представлено одно задание
- 13. Слайд 13
- 14. Последний этап1 рядЗадача индийского математика XII в.
- 15. Поздравляем! Вы завершили все задания. Пришло время подсчитать баллы и определить победителя.
- 16. Теорема, обратная к теореме Пифагора:позволяет проверить, является
- 17. Некоторые Пифагоровы тройки: (3,4,5), (6,8,10), (5,12,13),
- 18. Доказательство теоремы Пифагора:1)Достроим прямоугольник до квадрата со
- 19. Алгебраическое доказательство:1) Проведем высоту CH из вершины прямого
- 20. Геометрическое доказательство:1) Построим отрезок CD равный отрезку AB
- 21. На данный момент в научной литературе зафиксировано
- 22. Применение теоремы ПифагораТеорему Пифагора широко применяют и
- 23. Интересное о Пифагоре:Пифагор – это на самом
- 24. Важные открытия, связанные с именем Пифагора:в географии
- 25. Если дан нам треугольникИ притом с прямым
- 26. «Не гоняйся за счастьем: оно всегда находится в тебе самом».Пифагор.
Слайд 3История о Пифагоре:
Пифагор родился в 580 г. до н.э. в Древней
Пифагор перебрался в г. Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то отправился домой, чтобы там создать свою школу.
Слайд 4История теоремы:
Изучение вавилонских клинописных таблиц и древних
Согласно одной из легенд, знаменитую теорему Пифагор добыл как выигрыш с неизвестным математиком. Тот отдал свиток с теоремой Пифагору и сказал, что человек, который владеет этим свитком, будет известным не одно тысячелетие…
Слайд 5
Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть,
Слайд 7Теорема Пифагора
Теорема Пифагора — в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов
Слайд 103 этап
1 ряд
3 ряд
2 ряд
Команда которая первая даст правильный ответ получит
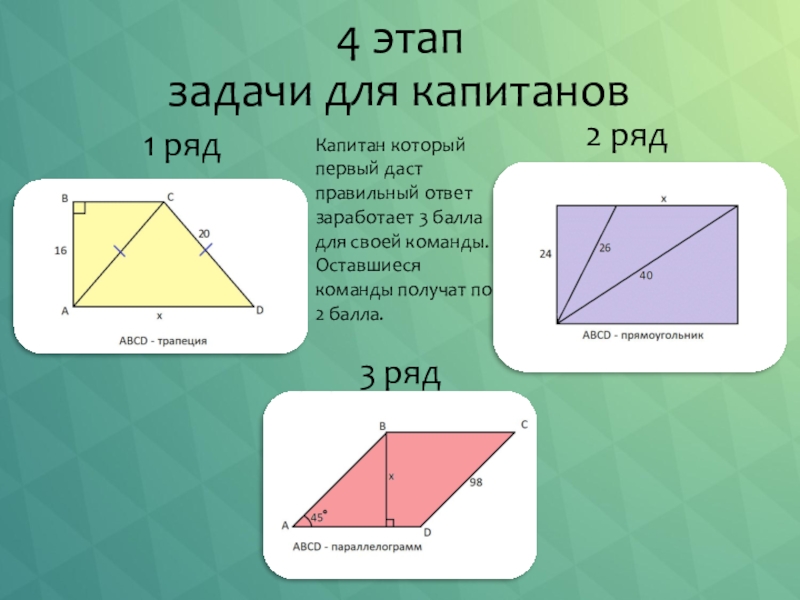
Слайд 114 этап
задачи для капитанов
1 ряд
2 ряд
3 ряд
Капитан который первый даст правильный
Слайд 12На следующем слайде будет представлено одно задание для всех команд. Команда
5 этап
задание на скорость
Слайд 14Последний этап
1 ряд
Задача индийского математика XII в. Бхаскары.
На берегу реки рос
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал.
И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка.
Верхушка склонилась у края реки, осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи: у тополя как велика высота?
2 ряд
Задача арабского математика XI в.
На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
3 ряд
В центре квадратного пруда, имеющего 10 футов в длину и ширину, растет тростник, возвышающийся на один фут над поверхностью воды. Если его пригнуть к берегу, к середине стороны пруда, то он своей верхушкой достигнет берега. Какова глубина пруда в современных единицах длины (1 фут приближенно равен 0,3 м)?
Команда которая первая даст правильный ответ получит 7 балла. Оставшиеся команды – 5 баллов.
Слайд 15
Поздравляем! Вы завершили все задания. Пришло время подсчитать баллы и определить
Слайд 16Теорема, обратная к теореме Пифагора:
позволяет проверить, является ли тот или иной
прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским», а тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению c2 = a2 + b2, т. е. служащие длинами сторон прямоугольных треугольников, Пифагоровыми.
Слайд 17Некоторые Пифагоровы тройки:
(3,4,5), (6,8,10), (5,12,13),
(9,12,15), (8,15,17), (12,16,20), (15,20,25), (7,24,25),
Слайд 18Доказательство теоремы Пифагора:
1)Достроим прямоугольник до квадрата со стороной
a
2)Площадь квадрата равна ( а + b)²
3)С другой стороны квадрат составлен из четырёх равных прямоугольных треугольников с площадью ½ аb и квадрата, площади с²
4) S=4 *1/2ab + с2 = 2bc + с2.
(а+b)2 =2ab+ с2.
с2 = а2 + b2.
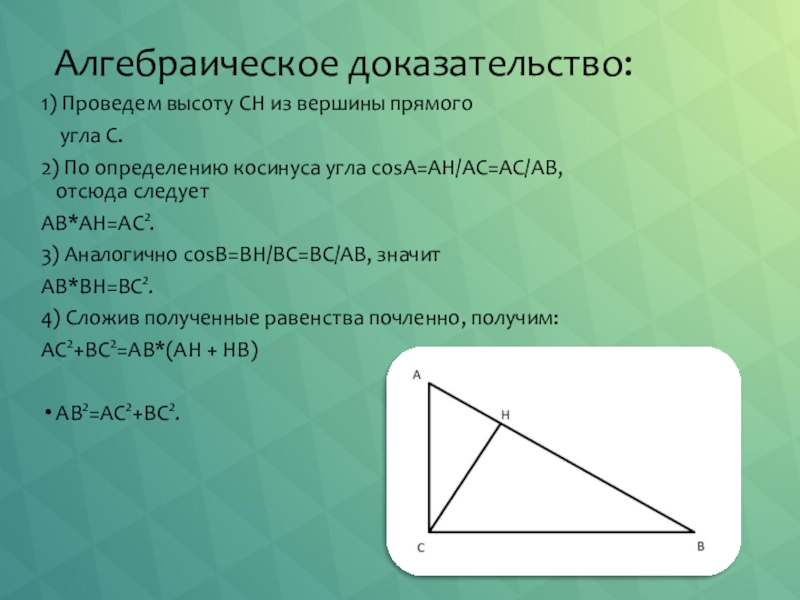
Слайд 19Алгебраическое доказательство:
1) Проведем высоту CH из вершины прямого
угла С.
2) По определению
AB*AH=AC2.
3) Аналогично соsВ=BH/BC=BC/AB, значит
AB*BH=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AH + HB)
AB2=AC2+BC2.
Слайд 20Геометрическое доказательство:
1) Построим отрезок CD равный отрезку AB на продолжении катета AC
2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна: SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано
в 1882 году Гарфилдом.
Слайд 21
На данный момент в научной литературе зафиксировано 367 доказательств теоремы Пифагора.
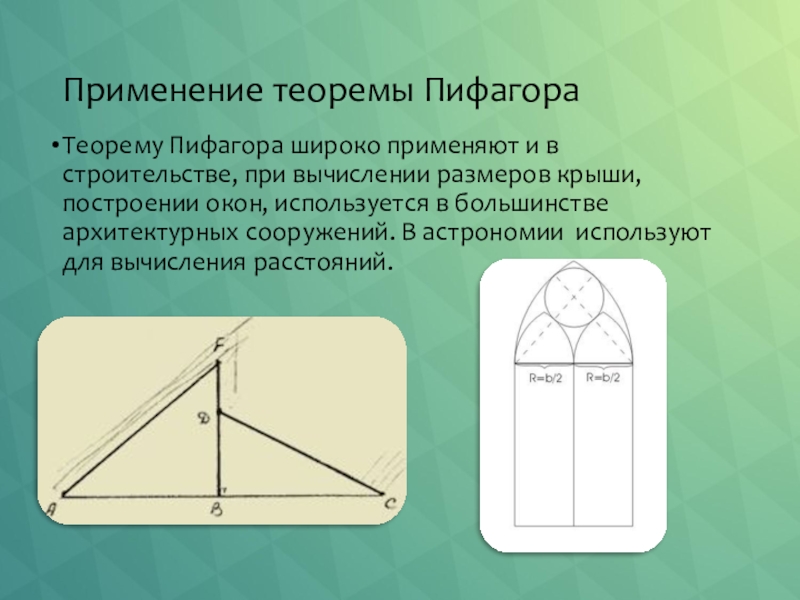
Слайд 22Применение теоремы Пифагора
Теорему Пифагора широко применяют и в строительстве, при вычислении
Слайд 23Интересное о Пифагоре:
Пифагор – это на самом деле прозвище, а не
(Пифагор - "убеждающий речью").
Увлекался спортом, побеждал в кулачном бою на Олимпийских играх.
Придумал специальную кружку, которая заставляла пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир.
Пифагор считал, что нельзя употреблять пищу животного происхождения. Он верил, что в животных переселяются души людей.
Слайд 24Важные открытия, связанные с именем Пифагора:
в географии и астрономии – представление
в музыке – зависимость между длиной струны арфы и звуком, который она издаёт;
в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).
Слайд 25Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.