- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрия. Материалы к уроку: Многоугольники
Содержание
- 1. Геометрия. Материалы к уроку: Многоугольники
- 2. УМК - Геометрия. 7 – 9классы: учебник
- 3. Слайд 3
- 4. Выпускник научится: объяснять, что такое ломаная;распознавать многоугольники,
- 5. На первом уроке можно ввести понятия ломаной,
- 6. Каждая замкнутая ломаная называется многоугольником, её звенья
- 7. Для усвоения понятия многоугольника можно выполнитьследующее упражнение
- 8. Многоугольником
- 9. Каждый многоугольник разделяет плоскость на две области
- 10. Внешняяобласть
- 11. ABCDEЭлементы многоугольника. Две вершины, принадлежащие одной стороне, называются соседними.
- 12. CFGB Сумма длин сторон AB, BC,
- 13. Чем отличаются эти многоугольники?
- 14. Выпуклые многоугольники
- 15. С целью лучшего усвоения понятия выпуклого много-угольника, после того как дано его определение, можновыполнить следующие упражнения:
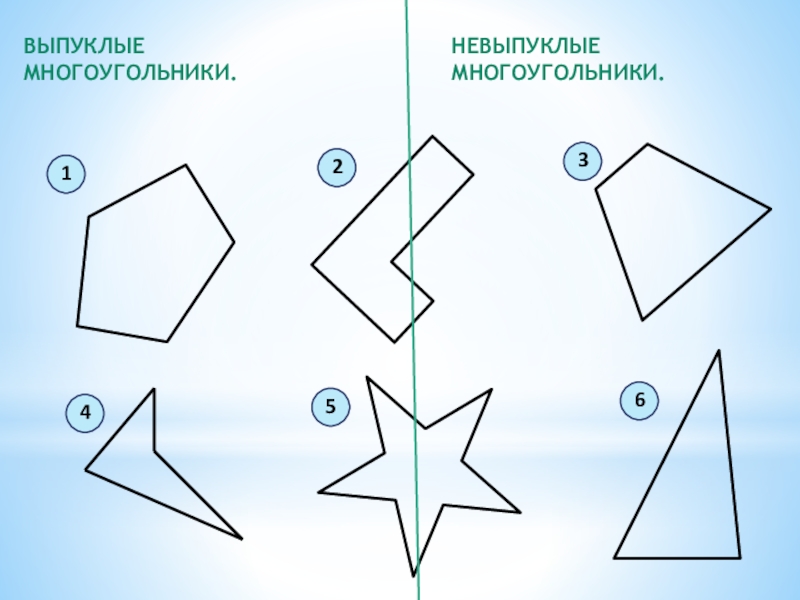
- 16. Распределите данные многоугольники на две группы. Объясните, по какому принципу вы это сделали.123456
- 17. Выпуклые многоугольники.Невыпуклые многоугольники.
- 18. Правильный многоугольникЭто выпуклый многоугольник, у которого все углы равны и все стороны равны .
- 19. Ученики работают индивидуально с учебником п.40,с.99-101.
- 20. Многоугольник, имеющий n углов называется n-угольником. Сколько сторон имеет n–угольник?
- 21. Физкультминутка: А теперь, ребята, встали. Быстро руки
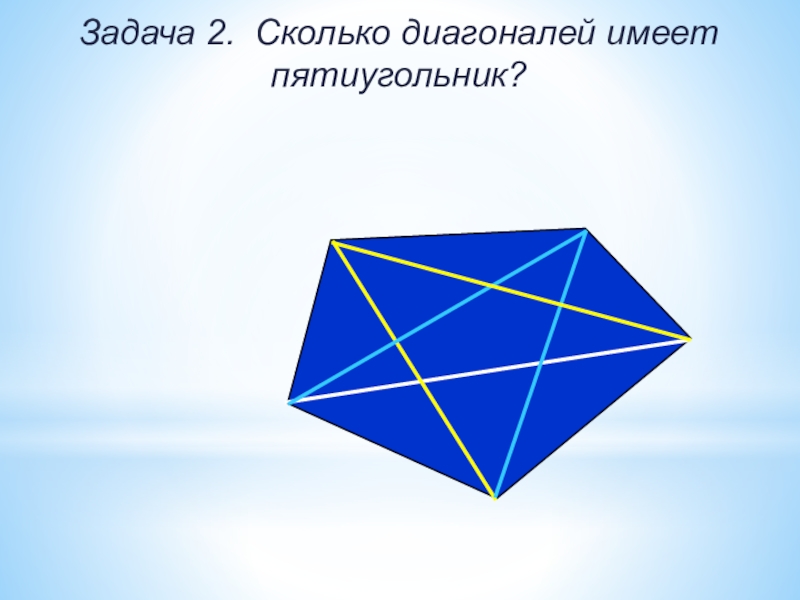
- 22. Задача 2. Сколько диагоналей имеет пятиугольник?
- 23. Упражнение 6Сколько диагоналей имеет:а) треугольник?0;б) четырехугольник?2;в) пятиугольник?5;г) шестиугольник?9;д) n-угольник?
- 24. Предлагается учащимся начертить выпуклый пятиугольник и провести
- 25. А Разделим этот многоугольник на несколько
- 26. Чему равна сумма углов треугольника?Найдите сумму всех углов этого пятиугольника.АS=180°∙ 3 =540°
- 27. Затем формулируется утверждение о сумме углов выпуклого
- 28. Сумма углов n-угольника равна S=180°∙(n-2)
- 29. Найдите сумму углов выпуклого:восьмиугольникадвенадцатиугольникаn=8. (8-2)·180=1080°n=12.
- 30. На втором уроке полезно провести самостоятельную работу обучающего характера.
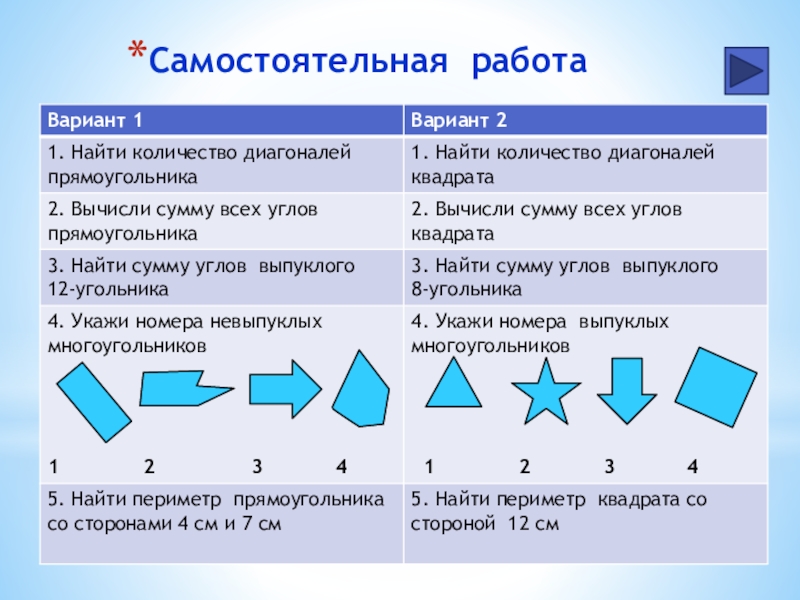
- 31. Самостоятельная работа
- 32. Самостоятельная работа (ответы)
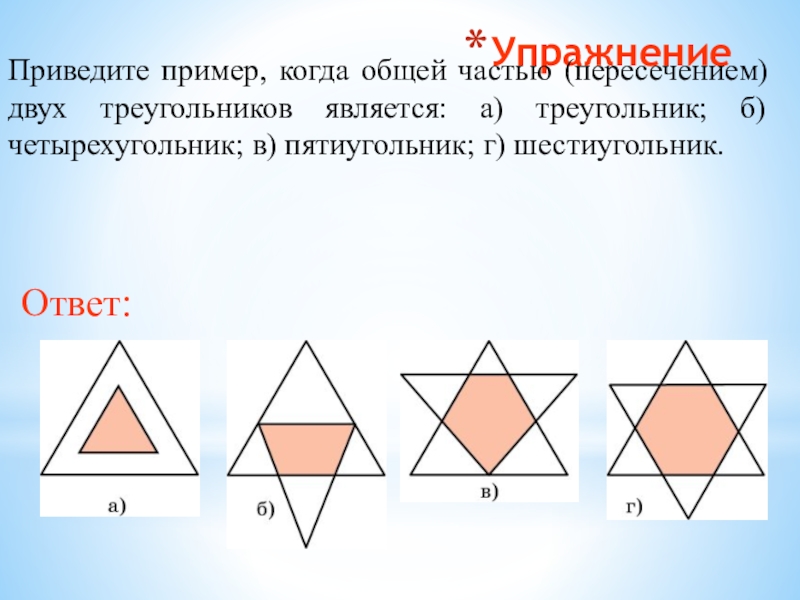
- 33. Упражнение Приведите пример, когда общей частью (пересечением)
- 34. Упражнение * Приведите пример, когда общей частью (пересечением) треугольника и четырехугольника является восьмиугольник.
- 35. Упражнение Сколько сторон имеют звездчатые многоугольники, изображенные на рисунке?Ответ: 5; 7; 7.
- 36. РефлексииУчитель просит детей в тетрадях заполнить таблицу
- 37. Спасибо за внимание
УМК - Геометрия. 7 – 9классы: учебник для общеобразовательных учреждений / [ Л.С. Атанасян, В.Ф. Бутузов и др.]. - 22-е изд. – М.: Просвещение, 2008.- Авторское тематическое планирование Л.С. Атанасяна и др. к учебнику Геометрия. 7
Слайд 1Многоугольники
Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников. Выпуклые и
невыпуклые многоугольники. Правильные многоугольники.
Слайд 2УМК
- Геометрия. 7 – 9классы: учебник для общеобразовательных учреждений /
[ Л.С. Атанасян, В.Ф. Бутузов и др.]. - 22-е изд. – М.: Просвещение, 2008.
- Авторское тематическое планирование Л.С. Атанасяна и др. к учебнику Геометрия.
7 – 9классы. Л.С. Атанасяна и др.
- Программы общеобразовательных учреждений. Геометрия. 7-9 классы. «Просвещение» 2008;
- Авторское тематическое планирование Л.С. Атанасяна и др. к учебнику Геометрия.
7 – 9классы. Л.С. Атанасяна и др.
- Программы общеобразовательных учреждений. Геометрия. 7-9 классы. «Просвещение» 2008;
Слайд 4Выпускник научится:
объяснять, что такое ломаная;
распознавать многоугольники, формулировать определение и приводить
примеры многоугольников, находить вершины, смежные стороны, диагонали;
показывать элементы многоугольников, внутреннюю и внешнюю области;
формулировать и доказывать теорему о сумме углов выпуклого многоугольника.
Выпускник получит возможность:
иметь четкое представление о многоугольнике, выпуклом и невыпуклом многоугольнике;
знать определения этих фигур, их свойства и признаки;
знать, что такое периметр многоугольника.
показывать элементы многоугольников, внутреннюю и внешнюю области;
формулировать и доказывать теорему о сумме углов выпуклого многоугольника.
Выпускник получит возможность:
иметь четкое представление о многоугольнике, выпуклом и невыпуклом многоугольнике;
знать определения этих фигур, их свойства и признаки;
знать, что такое периметр многоугольника.
Слайд 5На первом уроке можно ввести понятия ломаной, многоугольника и выпуклого многоугольника,
понятия вершин и смежных сторон , вывести формулу суммы углов выпуклого многоугольника.
На втором уроке больше пойдет закрепление темы различными заданиями.
Изучение темы можно начать с демонстрации рисунков
различных ломаных, отмечая по ходу показа, что все эти
фигуры составлены из отрезков так, что смежные отрезки
не лежат на одной прямой, и вводя связанную с этими
фигурами терминологию: ломаная, вершины, дли-
на ломаной, замкнутая ломаная.
На втором уроке больше пойдет закрепление темы различными заданиями.
Изучение темы можно начать с демонстрации рисунков
различных ломаных, отмечая по ходу показа, что все эти
фигуры составлены из отрезков так, что смежные отрезки
не лежат на одной прямой, и вводя связанную с этими
фигурами терминологию: ломаная, вершины, дли-
на ломаной, замкнутая ломаная.
Слайд 6Каждая замкнутая ломаная называется многоугольником, её звенья и вершины называются сторонами
и вершинами многоугольника,длина ломаной называется периметром многоугольника,
а многоугольник с n вершинами называется n-угольником.
а многоугольник с n вершинами называется n-угольником.
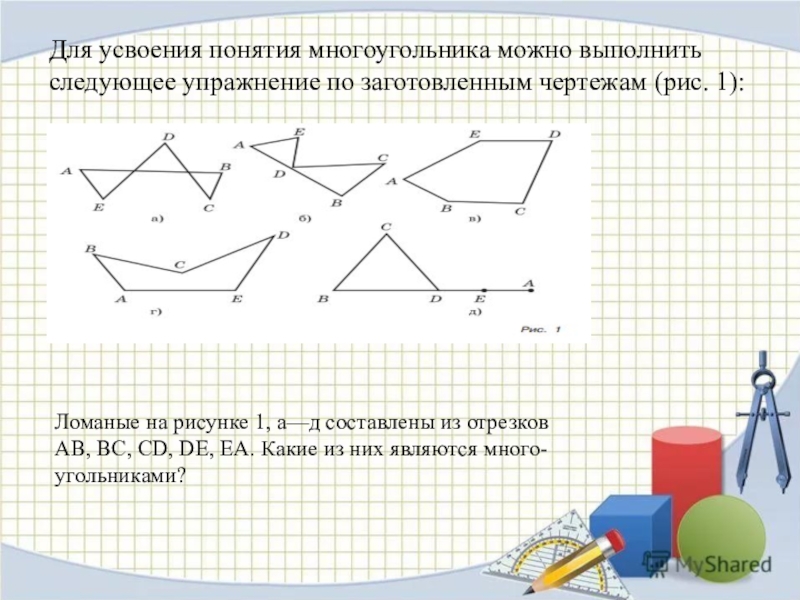
Слайд 7Для усвоения понятия многоугольника можно выполнить
следующее упражнение по заготовленным чертежам (рис.
1):
Ломаные на рисунке 1, а—д составлены из отрезков
АВ, ВС, CD, DE, ЕА. Какие из них являются много-
угольниками?
Слайд 8Многоугольником
называют фигуру, составленную из
отрезков так, что:
1) смежные отрезки не лежат на одной прямой;
2) несмежные отрезки не имеют общих точек.
1) смежные отрезки не лежат на одной прямой;
2) несмежные отрезки не имеют общих точек.
A
B
C
D
E
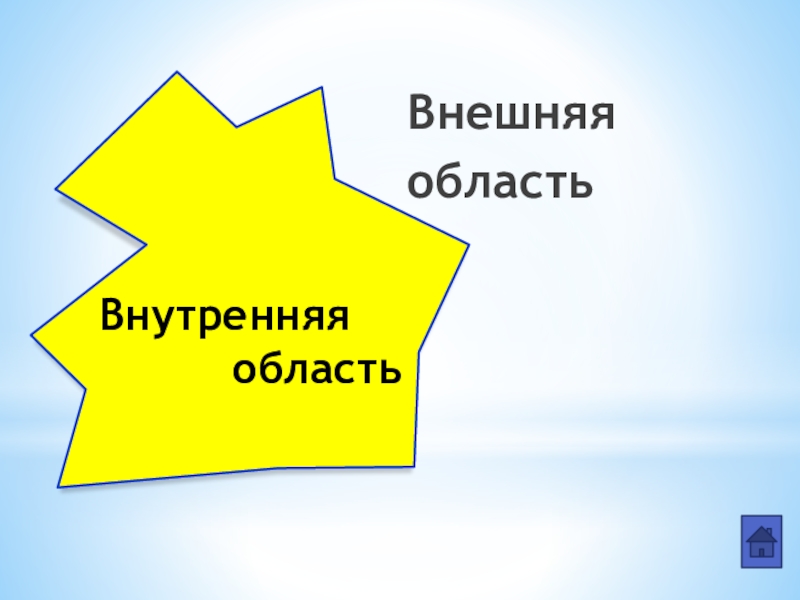
Слайд 9Каждый многоугольник разделяет плоскость на две области — внутреннюю и внешнюю,
причём фигуру, состоящую из многоугольника
и его внутренней области, также называют многоугольни-
ком .
и его внутренней области, также называют многоугольни-
ком .
Слайд 11A
B
C
D
E
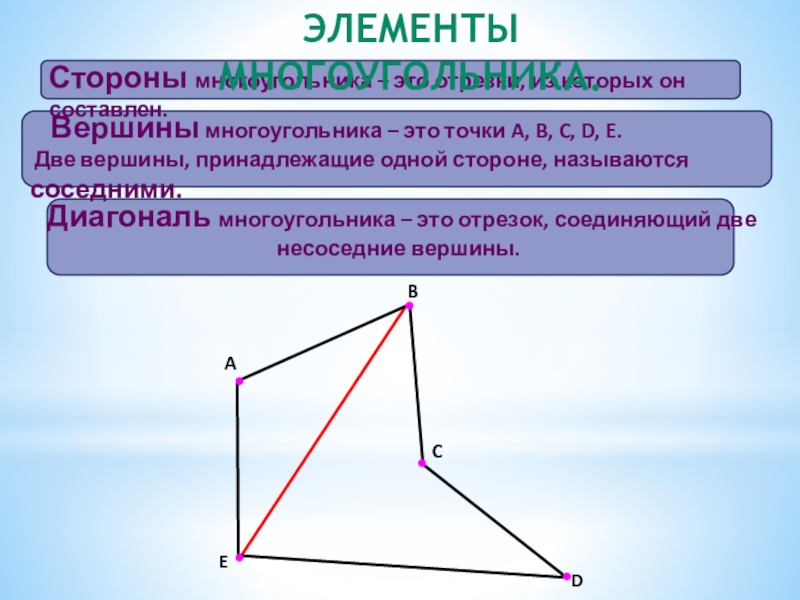
Элементы многоугольника.
Две вершины, принадлежащие одной стороне, называются соседними.
Слайд 12C
F
G
B
Сумма длин сторон
AB, BC, CD, DE, EF, FG,
GA
-называется
-называется
D
E
А
периметром многоугольника
Р=AB+ BC+ CD+ DE+ EF+ FG+GA
Слайд 14Выпуклые многоугольники
Определение:
Многоугольник называется
выпуклым,
если он лежит в одной полуплоскости
относительно любой прямой,
содержащей его сторону.
если он лежит в одной полуплоскости
относительно любой прямой,
содержащей его сторону.
Слайд 15С целью лучшего усвоения понятия выпуклого много-
угольника, после того как дано
его определение, можно
выполнить следующие упражнения:
выполнить следующие упражнения:
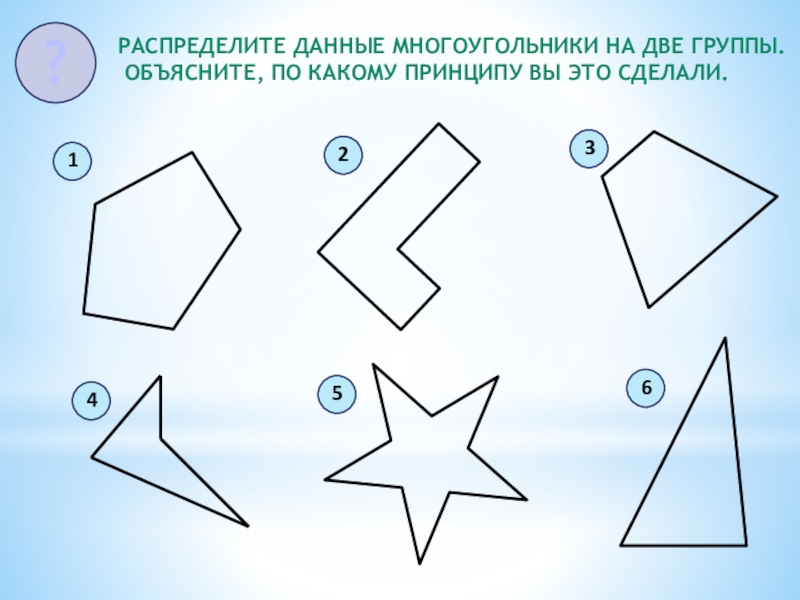
Слайд 16Распределите данные многоугольники на две группы.
Объясните, по какому принципу вы
это сделали.
1
2
3
4
5
6
Слайд 18Правильный многоугольник
Это выпуклый многоугольник, у которого все углы равны и все
стороны равны .
Слайд 19 Ученики работают индивидуально с учебником п.40,с.99-101. На полях ставят
номера вопросов, на которые нашли ответ и одновременно делают пометки: v- уже знал, + -новая информация, ?- есть вопросы, - -думал иначе (приём INSERT).
Слайд 21Физкультминутка:
А теперь, ребята, встали. Быстро руки вверх подняли,
В стороны, вперед,
назад. Повернулись вправо, влево, потянулись до предела. Тихо сели, вновь за дело.
Слайд 23Упражнение 6
Сколько диагоналей имеет:
а) треугольник?
0;
б) четырехугольник?
2;
в) пятиугольник?
5;
г) шестиугольник?
9;
д) n-угольник?
Слайд 24Предлагается учащимся начертить выпуклый пятиугольник и провести все диагонали из какой-нибудь
его вершины. Сколько при
этом образовалось треугольников? Найдите сумму углов
пятиугольника.
этом образовалось треугольников? Найдите сумму углов
пятиугольника.
Слайд 25А
Разделим этот многоугольник на несколько треугольников, проведя из вершины
А все диагонали.
Сколько получилось треугольников?
Сколько получилось треугольников?
Найти сумму углов многоугольника
Слайд 26 Чему равна сумма углов треугольника?
Найдите сумму всех углов этого пятиугольника.
А
S=180°∙
3 =540°
Слайд 27Затем формулируется утверждение о сумме углов выпуклого многоугольника и обсуждается план
доказательства.
Само доказательство можно предложить учащимся провести самостоятельно.
Само доказательство можно предложить учащимся провести самостоятельно.
Слайд 29Найдите сумму углов выпуклого:
восьмиугольника
двенадцатиугольника
n=8. (8-2)·180=1080°
n=12. (12-2)·180=1800°
Сколько сторон
имеет выпуклый многоугольник, если его сумма углов равна 2340°?
Решение:
(n-2)·180=2340
n-2=13
n=15
Ответ: многоугольник имеет 15 сторон.
Решение:
(n-2)·180=2340
n-2=13
n=15
Ответ: многоугольник имеет 15 сторон.
Слайд 33Упражнение
Приведите пример, когда общей частью (пересечением) двух треугольников является: а)
треугольник; б) четырехугольник; в) пятиугольник; г) шестиугольник.
Ответ:
Слайд 34Упражнение *
Приведите пример, когда общей частью (пересечением) треугольника и четырехугольника является
восьмиугольник.
Слайд 35Упражнение
Сколько сторон имеют звездчатые многоугольники, изображенные на рисунке?
Ответ: 5; 7;
7.
Слайд 36Рефлексии
Учитель просит детей в тетрадях заполнить таблицу INSERT, используя пометки сделанные
в п.40-41.
Учитель на доске заполняет графы «новая информация» и «есть вопросы».
Учитель на доске заполняет графы «новая информация» и «есть вопросы».