Автор:: Ковалева Людмила Леонидовна учитель математики, высшей квалификационной категории, «Почётный работник общего образования РФ», МБОУ «СОШ №77» г.Кемерово
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад внеклассного занятия по геометрии Бимедианы четырехугольника. Теорема Вариньона в теориях и задачах
Содержание
- 1. Презентация внеклассного занятия по геометрии Бимедианы четырехугольника. Теорема Вариньона в теориях и задачах
- 2. Актуальность темы:1. Данная тема является дополнением и
- 3. Цель работы: Расширить свой кругозор, узнать новую
- 4. Задачи:1. Изучить теоретический материал: ознакомиться с понятием
- 5. Вариньон Пьер.Вариньон Пьер(1654-1722)-выдающийся механик и учёный, член
- 6. Основные теоретические сведения.Определение.Бимедианы четырехугольника – это отрезки,
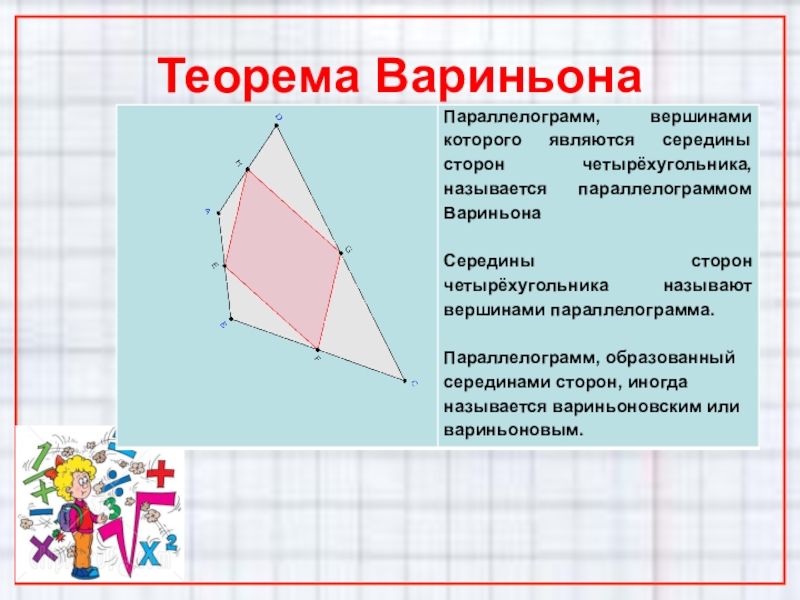
- 7. Теорема Вариньона
- 8. Теорема Вариньона. Теорема: Четырехугольник, образованный путем последовательного
- 9. Слайд 9
- 10. Следствия из теоремы.Следствие 1. Параллелограмм Вариньона является
- 11. Следствия из теоремы.Следствие 2.1. Параллелограмм Вариньона является
- 12. Следствия из теоремы.Следствие 2.2. Бимедианы четырёхугольника и
- 13. Следствия из теоремы.Следствие 3. Параллелограмм Вариньона является
- 14. Следствия из теоремы.Следствие 3.(теорема Эйлера).Для четырехугольника сумма
- 15. Следствия из теоремы.Следствие 4.(теорема о бабочках).Суммы площадей
- 16. Разбор задачзадачи из школьного курса геометрииЗадача 1.У
- 17. Разбор задачзадачи из школьного курса геометрииЗадача 2.Докажите, что середины сторон четырехугольника являются вершинами параллелограмма.Решение.См. теорему Вариньона.
- 18. Конкурсные задачи.Задача 3. Докажите, что если диагонали
- 19. Конкурсные задачи.Задача 5.Все стороны выпуклого четырехугольника площади
- 20. Конкурсные задачи.Задача 5.Все стороны выпуклого четырехугольника площади
- 21. Конкурсные задачи.Задача 4.Докажите, что площадь параллелограмма, образованного
- 22. Задача 6 Задача 7 Задача 8 На
- 23. Заключение«Нет ничего нового под солнцем, но есть
- 24. ЗаключениеДля этого был разобран весь теоретический материал,
- 25. СПАСИБО ЗА ВНИМАНИЕ !
- 26. Список литературы:Интернет-ресурсы ru.wikipedia.org/wiki/Вариньон,_ПьерФилипповский Г. Б. Параллелограмм Вариньона
- 27. интернет - ресурсы шаблона:images.yandex.ruluzan.ucoz.rushimrg.rusedu.net
Слайд 1Конспект внеклассного занятия по геометрии 8 класс «Бимедианы четырёхугольника. Теорема
Слайд 2Актуальность темы:
1. Данная тема является дополнением и углублением изученных в курсе
2. Применение опыта решения планиметрических задач с использованием теоремы Вариньона и следствий из нее помогает повысить уровень пространственного воображения и уровень логической культуры.
3. Изучение данной темы поможет более глубоко подготовиться к успешному участию в математических конкурсах и олимпиадах по математике.
4. Данная работа может быть использована для проведения практических занятий на элективных курсах с учащимися .
Слайд 3Цель работы:
Расширить свой кругозор, узнать новую информацию из раздела геометрии,
Объект исследования: Теорема Вариньона
Предмет исследования: геометрия
Слайд 4Задачи:
1. Изучить теоретический материал: ознакомиться с понятием “параллелограмм Вариньона”, рассмотреть способы
2. Сравнить способы решения с помощью обыденного решения задач, и используя теорему Вариньона.
3. Показать наглядно способы решения на примере конкурсных и олимпиадных заданий, применяя теорему Вариньона.
Слайд 5Вариньон Пьер.
Вариньон Пьер(1654-1722)-выдающийся механик и учёный, член Французской Академии Наук(с 1688
Изучал философию, математику в частности.
Место рождения-Каен.
Главнейшие научные заслуги Вариньона относятся к механике. Вариньон исходя из принципа равновесия рычага, начала параллелограмма сил и применяя теорему моментов, выводит условия равновесия всех простых машин.
Является первым учёным, который доказал, что середины сторон выпуклого четырёхугольника являются вершинами параллелограмма.
Слайд 6Основные теоретические сведения.
Определение.
Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон.
Одна
Слайд 8Теорема Вариньона.
Теорема: Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого
Слайд 10Следствия из теоремы.
Следствие 1. Параллелограмм Вариньона является ромбом тогда и только
Дано:
ABCD – четырехугольник;
KLMN – параллелограмм
Вариньона;
AC=BD
Доказать: KLMN – ромб
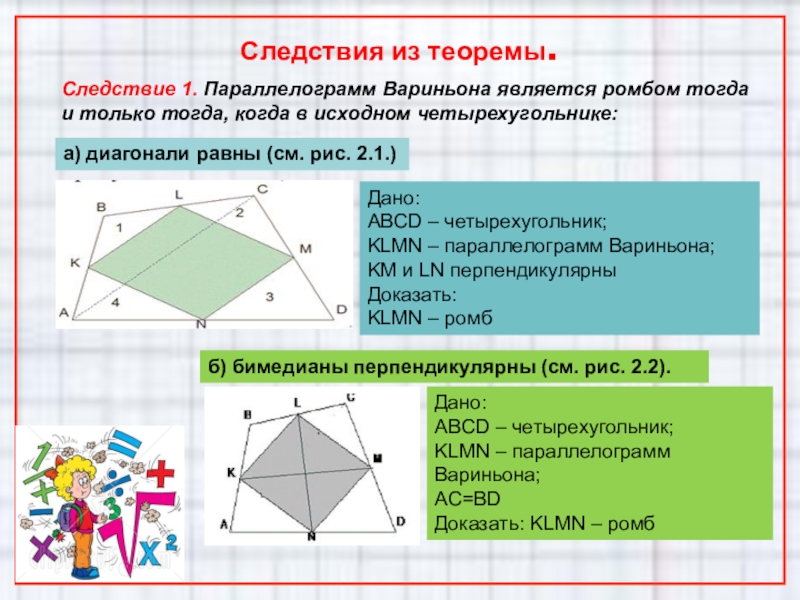
а) диагонали равны (см. рис. 2.1.)
б) бимедианы перпендикулярны (см. рис. 2.2).
Дано:
ABCD – четырехугольник;
KLMN – параллелограмм Вариньона;
KM и LN перпендикулярны
Доказать:
KLMN – ромб
Слайд 11Следствия из теоремы.
Следствие 2.1. Параллелограмм Вариньона является прямоугольником тогда и только
а) диагонали перпендикулярны (см. рис 3.1.);
Так как диагонали исходного четырехугольника перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Тогда параллелограмм Вариньона является прямоугольником (по признаку прямоугольника).
б) бимедианы равны (см. рис. 3.2.).
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
Слайд 12Следствия из теоремы.
Следствие 2.2. Бимедианы четырёхугольника и отрезок, соединяющий середины диагоналей,
Доказательство.
Пусть KM и LN – бимедианы ABCD, PQ – отрезок, соединяющий середины диагоналей АС и BD.
То, что бимедианы KM и LN точкой пересечения делятся пополам, следует из того, что эти отрезки являются диагоналями параллелограмма Вариньона. Поэтому нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам (рис.5, .1 и 5.2); обращаем внимание на то, что в невыпуклом четырехугольнике одна из диагоналей расположена вне четырехугольника).
Используя теорему о средней линии треугольника для соответствующих треугольников, имеем:LQ║CD║PN и PL║AB║NQ.
Тем самым, PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.
Слайд 13Следствия из теоремы.
Следствие 3. Параллелограмм Вариньона является квадратом тогда и только
а) диагонали равны и перпендикулярны(см. рис. 4.1.);
Так как диагонали исходного четырехугольника равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Тогда параллелограмм Вариньона является квадратом (по признаку квадрата).
б) бимедианы равны и перпендикулярны (см. рис. 4.2.).
Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
Слайд 14Следствия из теоремы.
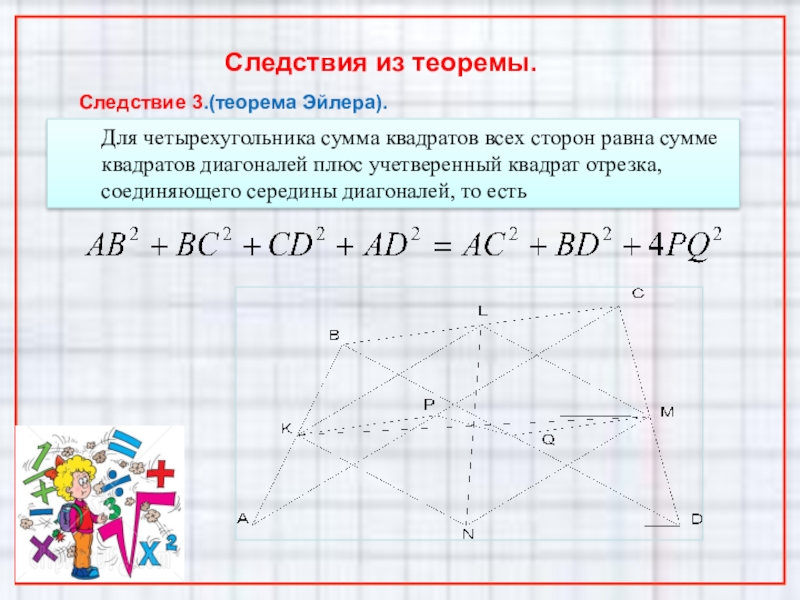
Следствие 3.(теорема Эйлера).
Для четырехугольника сумма квадратов всех сторон равна
квадратов диагоналей плюс учетверенный квадрат отрезка,
соединяющего середины диагоналей, то есть
.
Слайд 15Следствия из теоремы.
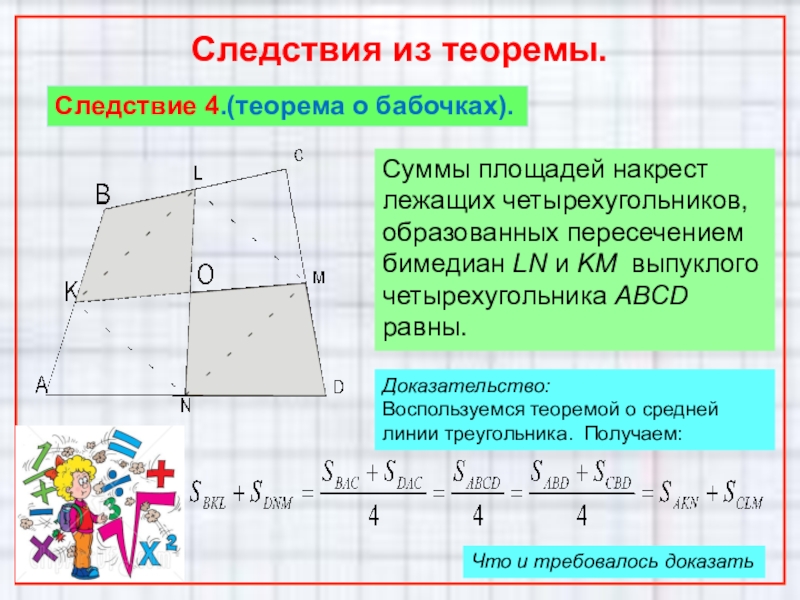
Следствие 4.(теорема о бабочках).
Суммы площадей накрест лежащих четырехугольников, образованных
Доказательство:
Воспользуемся теоремой о средней линии треугольника. Получаем:
Что и требовалось доказать
Слайд 16Разбор задач
задачи из школьного курса геометрии
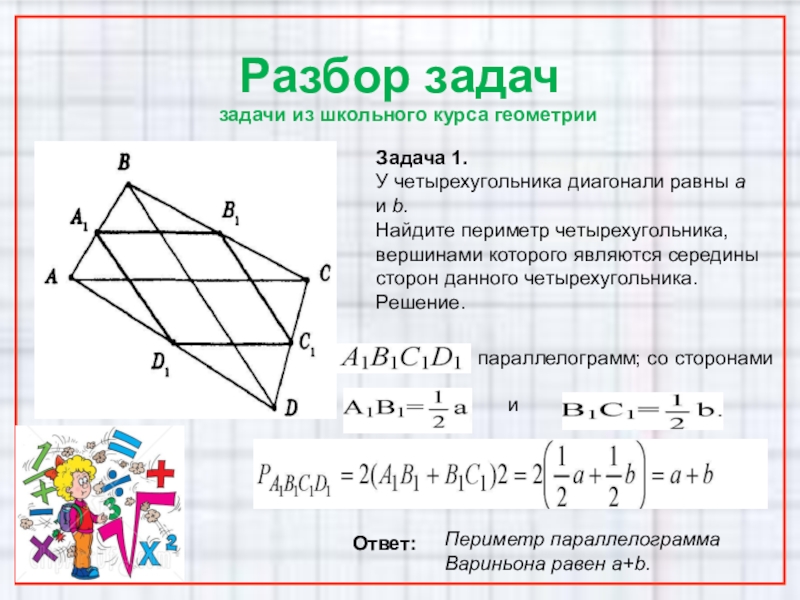
Задача 1.
У четырехугольника диагонали равны a
Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение.
параллелограмм; со сторонами
параллелограмм; со сторонами
и
Ответ:
Периметр параллелограмма
Вариньона равен a+b.
Слайд 17Разбор задач
задачи из школьного курса геометрии
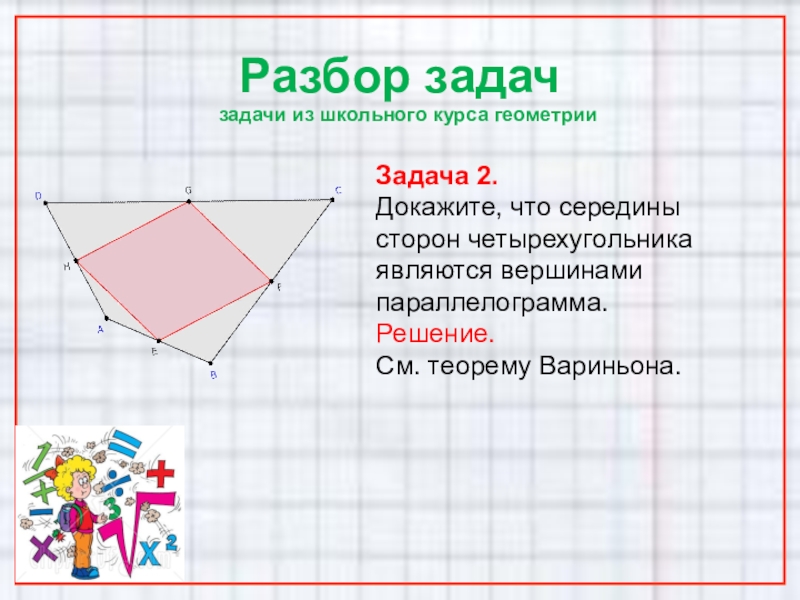
Задача 2.
Докажите, что середины сторон четырехугольника
Решение.
См. теорему Вариньона.
Слайд 18Конкурсные задачи.
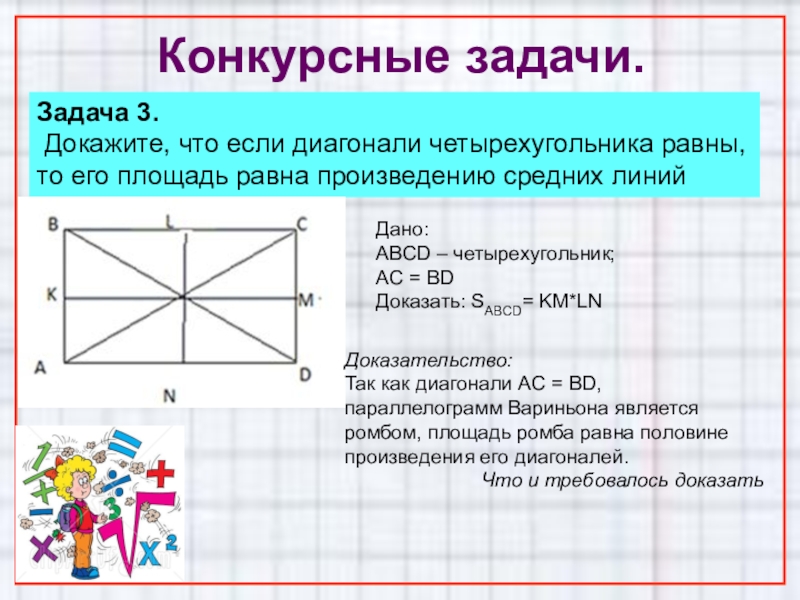
Задача 3.
Докажите, что если диагонали четырехугольника равны, то его
Дано:
ABCD – четырехугольник;
AC = BD
Доказать: SABCD= KM*LN
Доказательство:
Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.
Что и требовалось доказать
Слайд 19Конкурсные задачи.
Задача 5.
Все стороны выпуклого четырехугольника площади 1 разделены на 2n
Слайд 20Конкурсные задачи.
Задача 5.
Все стороны выпуклого четырехугольника площади 1 разделены на 2n
Слайд 21Конкурсные задачи.
Задача 4.
Докажите, что площадь параллелограмма, образованного прямыми, проходящими через вершины
Дано:
ABCD – четырехугольник;
AC = BD
Доказать: SABCD= KM*LN
Доказательство:
Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей.
Что и требовалось доказать
Слайд 22
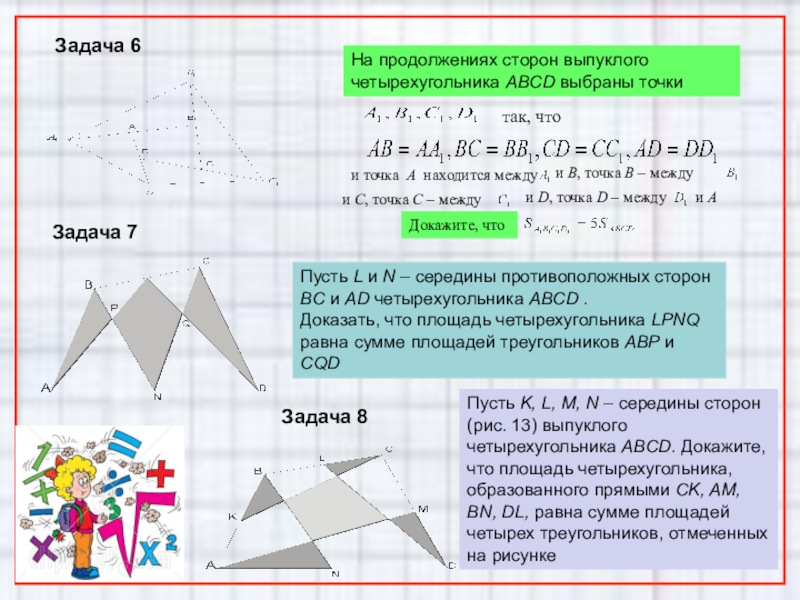
Задача 6
Задача 7
Задача 8
На продолжениях сторон выпуклого четырехугольника
так, что
Докажите, что
и точка A находится между
и B, точка B – между
и C, точка C – между
и D, точка D – между
и A
Пусть L и N – середины противоположных сторон BC и AD четырехугольника ABCD .
Доказать, что площадь четырехугольника LPNQ равна сумме площадей треугольников ABP и CQD
Пусть K, L, M, N – середины сторон (рис. 13) выпуклого четырехугольника ABCD. Докажите, что площадь четырехугольника, образованного прямыми CK, AM, BN, DL, равна сумме площадей четырех треугольников, отмеченных на рисунке
Слайд 23Заключение
«Нет ничего нового под солнцем, но есть кое-что старое, чего мы
Пьер Вариньон жил в 18 веке, но теорема Вариньона как нельзя актуальна именно в наши дни, когда чтобы всё успеть, необходимо гораздо больше, чем 24 часа в сутки.
Поэтому была поставлена цель: изучить теорему Вариньона и научиться применять ее на практике с наименьшими временными затратами.
Слайд 24Заключение
Для этого был разобран весь теоретический материал, решены задачи базового уровня,
Было подсчитано, что на решение задачи традиционным способом затрачивается больше времени, а зная теорему Вариньона и следствия из нее, доказательство сводится к одному-двум предложениям и занимает наименьшее время. При этом экономия времени на доказательство в среднем составляет около 15 минут. Таким образом, уже даже решение трех задач добавит дополнительные сорок пять минут (т.е. целый урок) на доказательство других, более сложных задач.
От этого повышается не только интерес к изучению данного предмета, но и сам процесс работы приносит удовлетворение.
Цель работы считаю достигнутой, задачи решены.
Слайд 26Список литературы:
Интернет-ресурсы ru.wikipedia.org/wiki/Вариньон,_Пьер
Филипповский Г. Б. Параллелограмм Вариньона решает задачи //Математика в
В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 – №22.
Геометрия: Учебник для 7 – 9 кл. общеобразовательных учреждений /Л. С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др, – М.: Просвещение, 2008.
Геометрия: Доп. главы к шк. учеб. 8 кл.: Учеб. пособие для учащихся школ и классов с углубленным изучением математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1996.
Интернет-ресурсы easymath.com.ua/
Погорелов А. В. Геометрия: Учеб. для 7 – 11 кл. сред. шк.- М.: Просвещение,1990.- 384 с.
Штейнгауз Г.Математический калейдоскоп. – М.:наука,1981.
Прасолов В.В. задачи по планиметрии. – Т.1, 2. – М.: Наука,1995.
Коксетер Г. С. М., Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука,1978.
В. Вавилов, П. Красников. Бимедианы четырехугольника//Математика. 2006 - №22.