- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Классификация картографических проекций и виды проекций
Содержание
- 1. Классификация картографических проекций и виды проекций
- 2. Математически определенный способ отображения поверхности Земли (либо другого
- 3. — равноугольные, или конформные; — равновеликие, или
- 4. Равноугольные проекции. Основным свойством равноугольных, или конформных,
- 5. Равновеликие проекции. Равновеликие, или эквивалентные, проекции не
- 6. Равнопромежуточные проекции. Равнопромежуточными называются проекции, сохраняющие постоянство
- 7. Произвольные проекции. Проекции, не относящиеся ни к
- 8. — конические; — азимутальные; — цилиндрические; Классификация виду меридианов и параллелей нормальной картографической сетки проекции
- 9. Конические проекции. Коническими называются проекции, у которых
- 10. Азимутальные проекции. Азимутальными называются проекции, у которых
- 11. Цилиндрические проекции. Цилиндрическими проекциями называются такие, параллели
- 12. Конец!
Математически определенный способ отображения поверхности Земли (либо другого небесного тела, или в общем смысле, любой искривлённой поверхности) на плоскость.Определение:
Слайд 2Математически определенный способ отображения поверхности Земли (либо другого небесного тела, или в
общем смысле, любой искривлённой поверхности) на плоскость.
Определение:
Слайд 3— равноугольные, или конформные;
— равновеликие, или эквивалентные (равноплощадные);
— равнопромежуточные (эквидистантные);
— произвольные.
Классификация
по характеру искажений:
Слайд 4Равноугольные проекции.
Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых
фигур на карте соответствующим фигурам на поверхности Земли. Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом. Однако при сохранении неискаженными углов и направлений в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.
Условие равноугольности картографической проекции можно записать следующим образом:
a = b; m = n.
Слайд 5Равновеликие проекции.
Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но
сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте. Бесконечно малый кружок на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.
Математическое условие равновеликости можно записать следующим образом:
p = ab = 1.
На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.
Слайд 6Равнопромежуточные проекции.
Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных
направлений. Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга. Таким образом, основное условие равнопромежуточных проекций выражается так:
а=1 или b= 1;
р = а или р = b.
Искажение углов и площадей в равнопромежуточной проекции выражается формулами:
sin ω = (a - 1) : (a + 1);
vp = a - 1.
где vр — увеличение масштаба площадей.
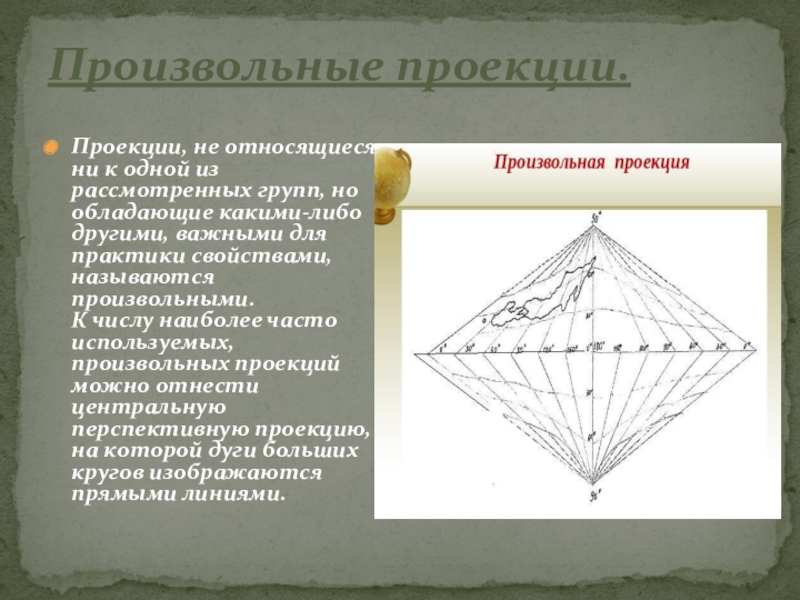
Слайд 7Произвольные проекции.
Проекции, не относящиеся ни к одной из рассмотренных групп, но
обладающие какими-либо другими, важными для практики свойствами, называются произвольными.
К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.
Слайд 8— конические;
— азимутальные;
— цилиндрические;
Классификация виду меридианов и параллелей нормальной картографической сетки
проекции
Слайд 9Конические проекции.
Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми,
сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов (рисунок). Конические проекции определяются уравнениями:
λ = α λo
ρ = f (φ) (74)
где λ — разность долгот на проекции;
α — коэффициент пропорциональности (обычно меньше единицы), называемый показателем конической проекции;
λо — угол между меридианами в натуре;
ρ — радиус параллели сетки.
Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса. Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса.
Слайд 10Азимутальные проекции.
Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми
линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов (рисунок-круг). Уравнения меридианов и параллелей нормальной сетки в азимутальных проекциях имеют вид
δ = λo
ρ = f (φ) (75)
где δ —угол между меридианами нормальной сетки;
λo — угол между меридианами на глобусе;
ρ —-радиус параллели .нормальной сетки.
Слайд 11Цилиндрические проекции.
Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых
изображаются взаимно перпендикулярными прямыми. Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.
Общие уравнения цилиндрических проекций имеют вид
x = f (φ)
y = C λ (76)