- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тема занятия Использование графиков тригонометрических функций для решения физических задач
Содержание
- 1. Тема занятия Использование графиков тригонометрических функций для решения физических задач
- 2. « Нет ни одной области математики, которая
- 3. Способы построения графикау=sin хСвойства тригонометрических функций.Таблица Правила преобразований функций
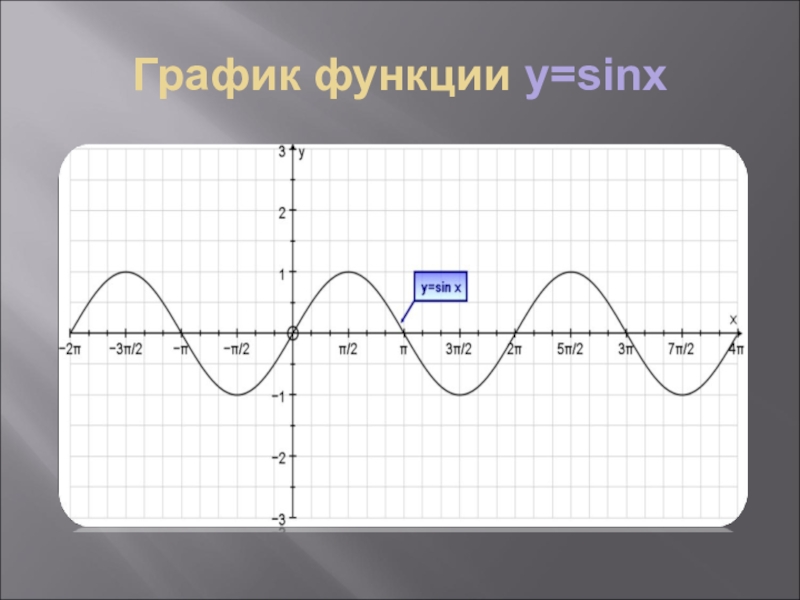
- 4. График функции y=sinx
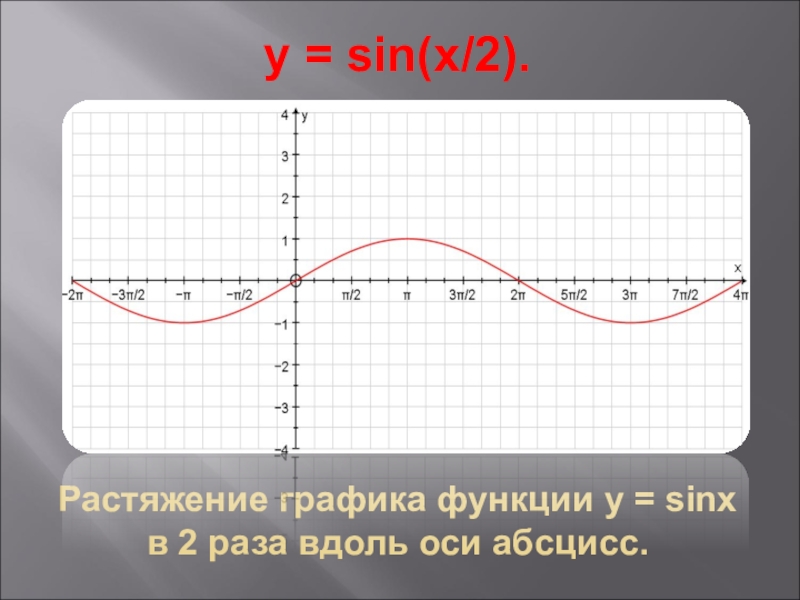
- 5. y = sin(x/2).
- 6. y = sin(x/2 + π/6).
- 7. y = 3sin(x/2 + π/6).
- 8. Записать уравнение функции по графику, изображенному на рисунке y = -2 sin x/24-2-2π2π3π- π-2π0
- 9. маятник на нитиПружинный маятникмаятник Фуко
- 10. Слайд 10
- 11. Начиная с XVII в., тригонометрические функции начали
- 12. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ x = Xm
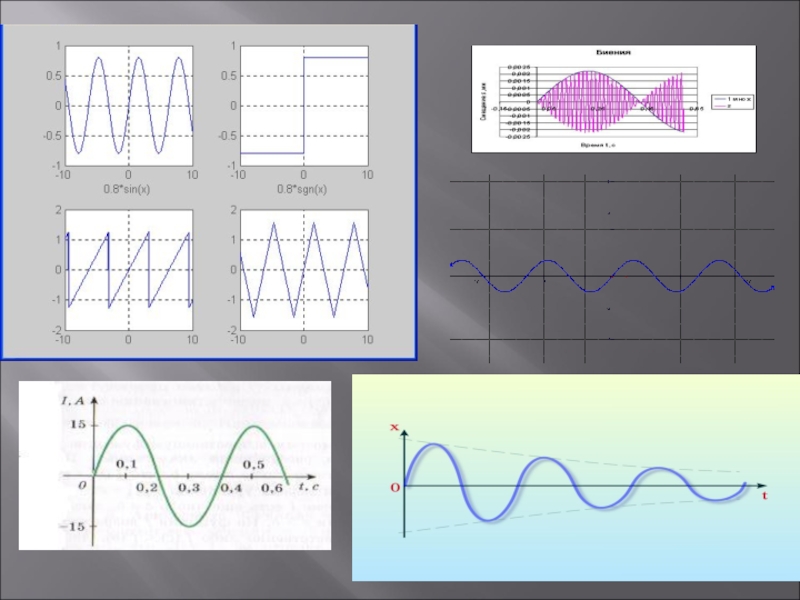
- 13. Слайд 13
- 14. Решение задачиДано: φ=0 Решение:А=2см
- 15. Определение основных характеристик колебательного движения по графикуОпределите
Слайд 1ТЕМА ЗАНЯТИЯ «ИСПОЛЬЗОВАНИЕ ГРАФИКОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ДЛЯ РЕШЕНИЯ ФИЗИЧЕСКИХ ЗАДАЧ» ВЫПОЛНИЛ: ПРЕПОДАВАТЕЛЬ
Слайд 2« Нет ни одной области математики, которая когда-нибудь не окажется применимой
Н.И. Лобачевский.
“ Физика без математики – это только природоведение”
Слайд 3Способы построения
графика
у=sin х
Свойства тригонометрических функций
.Таблица
Правила преобразований функций
Слайд 8 Записать уравнение функции по графику, изображенному на рисунке
y =
4
-2
-2
π
2π
3π
- π
-2π
0
Слайд 11
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений,
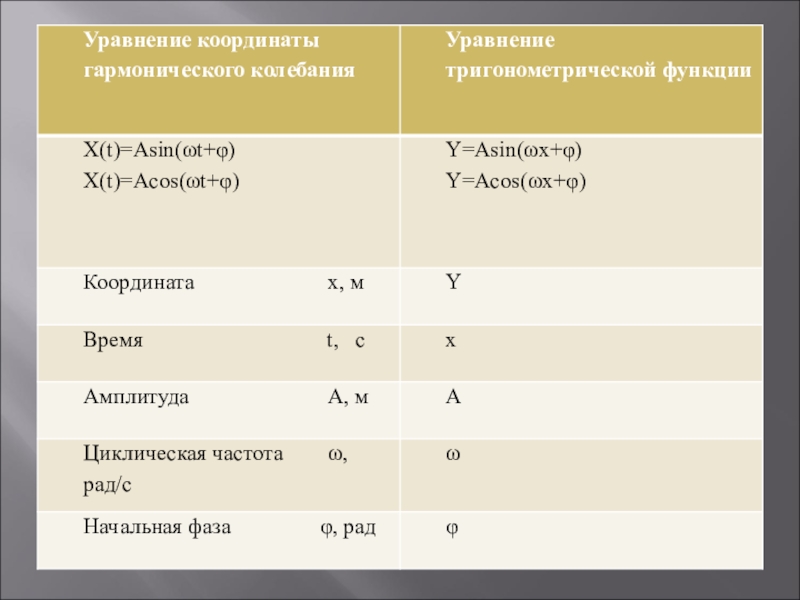
Слайд 12ОСНОВНЫЕ ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ
x = Xm sin(ω t + φ0)
x –
А – модуль максимального смещения точки от положения равновесия называется амплитудой
Т – время одного полного колебания называется периодом;
Т = t/n, где n – число полных колебаний
число колебаний в единицу времени называется частотой;υ = 1/Т – линейная частота колебанийυ= n/t; υ= [ Гц ]
ω = 2π/Т –циклическая частота колебаний ω = [ рад/с ]
φ = ωt + φ0 – фаза колебаний, которая определяет состояние колебательной системы в любой момент времени; φ = [ рад ]
Слайд 14Решение задачи
Дано: φ=0 Решение:
А=2см
N= ν = 1/Т =
t = ω= 2пν=
Т-? ν-? y(x) = А cos(ωt + φ) ω-? X(t)-? Построим график:
График x(t)
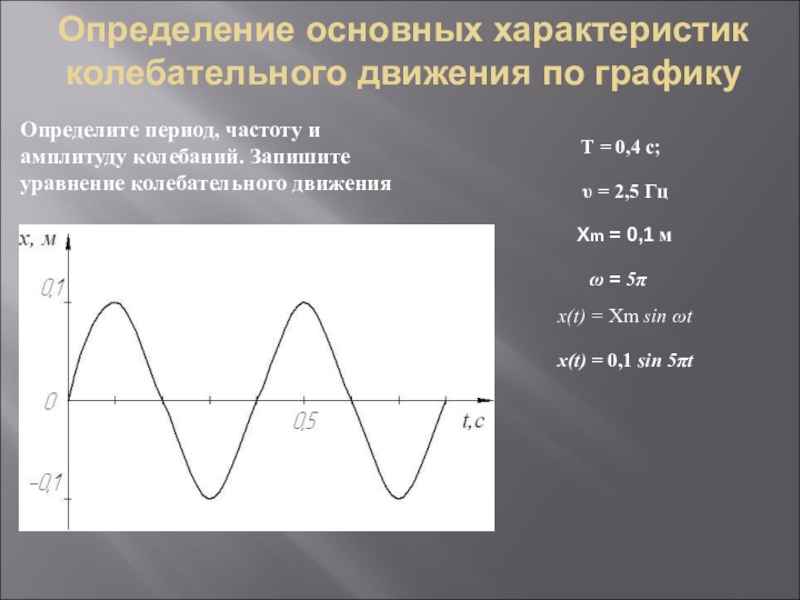
Слайд 15Определение основных характеристик колебательного движения по графику
Определите период, частоту и амплитуду
Т = 0,4 с;
Xm = 0,1 м
υ = 2,5 Гц
ω = 5π
x(t) = Xm sin ωt
x(t) = 0,1 sin 5πt