- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Законы сохранения в механике 10 класс
Содержание
- 1. Презентация Законы сохранения в механике 10 класс
- 2. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСАЗаконы сохранения механических величин не
- 3. Импульс материальной точкиВторой закон НьютонаЕсли на тело
- 4. Произведение силы на время её действия называют
- 5. Силы, возникающие в результате взаимодействия тела, принадлежащего
- 6. Закон сохранения импульса: если сумма внешних сил, действующих
- 7. Вывод второго закона НьютонаВторой закон Ньютона выводится
- 8. Вывод третьего закона НьютонаДля выведения третьего закона Ньютона понадобится закон сохранения импульса:
- 9. Реактивное движениеРеактивным движением называют движение тела, возникающее
- 10. Закон сохранения импульса выполняется для любых систем
- 11. Механическая работа и мощность силыВоздействия на тела
- 12. Работа постоянной силы равна произведению модулей силы
- 13. Если направление силы и перемещения совпадают, то
- 14. Джоуль — это работа, совершаемая силой 1 Н
- 15. Мощность — это отношение работы А к
- 16. Работа силы тяжести и силы упругости. Консервативные
- 17. Из прямоугольного треугольника BDCТело бросили вертикально вверх
- 18. Работа силы тяжести не зависит от формы
- 19. Работа силы упругости.Вычислим работу, которую совершает пружина
- 20. Если начальное и конечное состояния пружины совпадают,
- 21. Работа сил упругости зависит лишь от деформаций
- 22. Работа силы тяжести:
- 23. ЭНЕРГИЯЭнергия – способность тела совершить работуКинетическая энергия
- 24. КИНЕТИЧЕСКАЯ ЭНЕРГИЯФизическая величина, равная половине произведения
- 25. Так как точка движется с постоянным ускорением,
- 26. Если на точку действует несколько сил, то
- 27. 1. Как выглядит график изменения кинетической энергии
- 28. Потенциальная энергия1. Потенциальная энергия тела поднятого над
- 29. Согласно теореме об изменении кинетической энергии работа
- 30. Величину, равную произведению массы m тела на
- 31. Еп = Еп2 - Еп1А = Еп1 — Еп2 = -(Еп2 —
- 32. Различия между потенциальной и кинетической энергиейКинетическая энергия
- 33. Закон сохранения энергии в механикеВ замкнутой системе
- 34. ΔЕк = Aт ΔЕп = -Ат ΔЕк = -ΔЕп. Равенство означает, что увеличение
- 35. Общий закон сохранения энергии Энергия не создаётся
- 36. Сила трения совершает отрицательную работу и уменьшает
- 37. Работа сил трения, действующих внутри системы, всегда отрицательна и механическая энергия в замкнутой системе убывает:DE = Атр
- 38. СТОЛКНОВЕНИЕ УПРУГИХ ШАРОВПрименим закон сохранения энергии для
- 39. Закон сохранения импульса в проекциях на ось
- 40. Применим эти формулы для двух частных случаев.
- 41. 2. Оба шара имеют одинаковую массу, тогда шары
Слайд 2ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Законы сохранения механических величин не теряют своего значения. Они
Закон сохранения импульса связан с однородностью пространства, с тем, что все точки пространства совершенно равноправны. Перенос (сдвиг) в пространстве какой-либо механической системы никак не влияет на процессы внутри неё.
Введём новую физическую величину — импульс материальной точки. Дадим другую формулировку второго закона Ньютона.
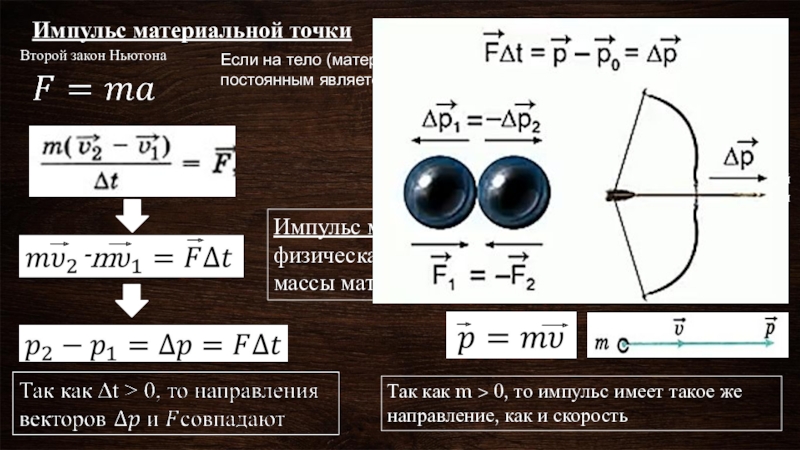
Слайд 3Импульс материальной точки
Второй закон Ньютона
Если на тело (материальную точку) действует постоянная
начальное и конечное значения скорости материальной точки
Импульс материальной точки — это векторная, физическая величина, равная произведению массы материальной точки на её скорость:
Так как m > 0, то импульс имеет такое же направление, как и скорость
Слайд 4Произведение силы на время её действия называют импульсом силы.
Второй закон Ньютона
Изменение импульса материальной точи равно импульсу действующей на нее силы.
1 ед. импульса = 1 кг • 1 м/с = 1 кг • м/с.
Импульс тела равен сумме импульсов его отдельных элементов.
Слайд 5Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не
Силы, возникающие в результате взаимодействия тел, принадлежащих системе, называются внутренними силами.
Импульс системы тел могут изменить только внешние силы, причём изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы.
геометрическая сумма всех внешних сил, действующих на тела системы.
Слайд 6Закон сохранения импульса: если сумма внешних сил, действующих на тела системы, равна
Тела могут только обмениваться импульсами, суммарное же значение импульса не изменяется. Сохраняется, только, векторная сумма импульсов, а не сумма их модулей.
1) Если даже на тела системы действуют внешние силы, но их сумма равна нулю, то импульс системы всё равно сохраняется.
2) Если сумма внешних сил не равна нулю, но сумма проекций сил на какое- то направление равна нулю, то проекция суммарного импульса системы на это направление не меняется.
3) Если внешние силы много меньше внутренних сил, то можно считать, что импульс системы сохраняется.
Слайд 7Вывод второго закона Ньютона
Второй закон Ньютона выводится из соотношения импульса силы
Слайд 8
Вывод третьего закона Ньютона
Для выведения третьего закона Ньютона понадобится закон
Слайд 9Реактивное движение
Реактивным движением называют движение тела, возникающее при отделении некоторой его
Так как вследствие истечения струи ракета движется с ускорением, то можно считать, что на ракету действует сила, называемая реактивной силой.
Главная особенность реактивной силы в том, что она возникает в результате взаимодействия частей системы без какого-либо взаимодействия с внешними телами.
Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.
Слайд 10Закон сохранения импульса выполняется для любых систем — будь то космические
Д/З.
1. РЕАКТИВНЫЕ ДВИГАТЕЛИ.
2. Реактивное движение совершает кальмар. Как это ему удаётся?
3. Будет ли увеличиваться скорость ракеты, если скорость истечения газов относительно ракеты меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой?
Слайд 11Механическая работа и мощность силы
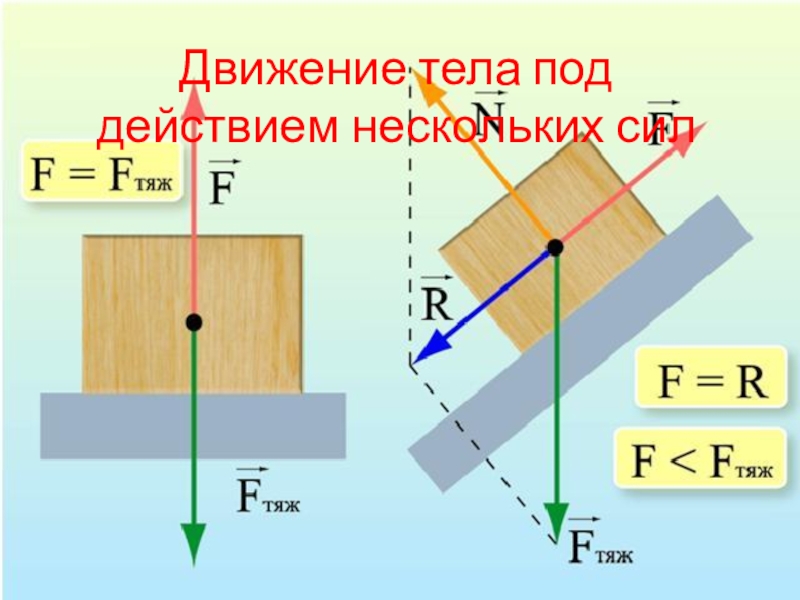
Воздействия на тела сил, приводящих к изменению
Слайд 12Работа постоянной силы равна произведению модулей силы и перемещения точки приложения
Если на тело действует несколько сил, то полная работа (алгебраическая сумма работ всех сил) равна работе равнодействующей силы.
Слайд 13Если направление силы и перемещения совпадают, то работа положительна; если эти
Работа равна нулю, если
а) угол между силой и перемещением 90º
б) сила не действует, а тело движется
в) сила действует, а тело покоится
Слайд 14Джоуль — это работа, совершаемая силой 1 Н на перемещении 1 м,
Слайд 15Мощность — это отношение работы А к интервалу времени Δt, за
Мощность равна 1 Вт, если работа, равная 1 Дж, совершается за 1 с.
Слайд 16Работа силы тяжести и силы упругости. Консервативные силы
Вычислим сначала работу силы
В начальный момент времени тело находилось на высоте h1 над поверхностью Земли, а в конечный момент времени — на высоте h2.
Модуль перемещения тела
Направления векторов силы тяжести и перемещения совпадают.
Согласно определению работы
Слайд 17Из прямоугольного треугольника BDC
Тело бросили вертикально вверх из точки, расположенной на
Работу силы тяжести запишем так:
Если же тело перемещается по прямой так, что направление перемещения составляет угол α с направлением силы тяжести то работа силы тяжести равна:
Слайд 18Работа силы тяжести не зависит от формы траектории, а зависит только
1) Перемещение тела из точки B в D по траектории BCD
2) Перемещение тела из точки B в D по траектории DEB
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю, называют консервативными силами.
Слайд 19Работа силы упругости.
Вычислим работу, которую совершает пружина при перемещении груза.
На (рис.
Если пружина растянута, то она действует на шар с силой (рис.б), направленной к положению равновесия шара, в котором пружина не деформирована. Вычислим работу силы упругости при перемещении шара из точки с координатой x1 в точку с координатой x2. Из (рис. в) видно, что модуль перемещения равен:
Слайд 20Если начальное и конечное состояния пружины совпадают, то суммарная работа силы
Вычислить работу силы упругости по формуле
A = F | Δr| cos α нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком зависимости модуля силы упругости от координаты шара.
Работа будет численно равна площади трапеции BCDM.
Слайд 21Работа сил упругости зависит лишь от деформаций пружины в начальном и
Слайд 22Работа силы тяжести: работа по
Работа силы упругости: траектории
равна нулю
Работа силы трения:
A = - FTP s
Слайд 23ЭНЕРГИЯ
Энергия – способность тела совершить работу
Кинетическая энергия - энергия движущегося тела
Потенциальная
Если система тел может совершить работу, что она обладает энергией.
Энергия в механике — величина, определяемая состоянием системы — положением тел и их скоростями; изменение энергии при переходе системы из одного состояния в другое равно работе внешних сил.
Слайд 24КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Физическая величина, равная половине произведения массы тела на квадрат
Направление силы совпадает с направлением скорости материальной точки. В этом случае направления вектора перемещения r и вектора силы F совпадают (рис.). Поэтому работа силы:
А = F|Δr|
Слайд 25Так как точка движется с постоянным ускорением, то изменение её координаты
А = FΔx.
F = mа
А = Ек2 - Ек1 = ΔЕк
Теорема об изменении кинетической энергии: Изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Слайд 26Если на точку действует несколько сил, то изменение её кинетической энергии
Вывод: Изменение кинетической энергии материальной точки зависит от начальной и конечной скоростей точки и не зависит от того, каким образом изменялась её скорость, под действием каких сил происходило это изменение.
Слайд 271. Как выглядит график изменения кинетической энергии материальной точки в зависимости
2. Какую работу совершила сила, действующая на точку, если направление её скорости изменилось на противоположное, а модуль её остался без изменения?
3. Зависит ли кинетическая энергия материальной точки от выбора системы отсчёта?
4. Может ли кинетическая энергия иметь отрицательное значение?
Д/З
Слайд 28Потенциальная энергия
1. Потенциальная энергия тела поднятого над Землей на высоту h:
Ep = mgh.
2. Потенциальная энергия деформированного тела:
х – удлинение
к - жесткость
Слайд 29Согласно теореме об изменении кинетической энергии работа силы, действующей на тело,
Если же силы взаимодействия между телами являются консервативными, то работу таких сил можно представить в виде разности двух значений величины, зависящей от взаимного расположения тел (или частей одного тела):
Слайд 30Величину, равную произведению массы m тела на ускорение свободного падения g
Еп = mgh
Величину, равную половине произведения коэффициента упругости k тела на квадрат удлинения или сжатия х, называют потенциальной энергией упруго деформированного тела:
Слайд 31Еп = Еп2 - Еп1
А = Еп1 — Еп2 = -(Еп2 — Еп1) = -ΔЕп,
ΔЕп = -А
Изменение
Работа консервативных сил определяет не саму потенциальную энергию, а её изменение.
Изолированная система тел стремится к состоянию, в котором её потенциальная энергия минимальна.
Если не удерживать тело, то оно падает на землю (h = 0); если отпустить растянутую или сжатую пружину, то она вернётся в недеформированное состояние (х = 0)
Слайд 32Различия между потенциальной и кинетической энергией
Кинетическая энергия зависит только от скоростей
Кинетическая энергия всегда положительна, а потенциальная энергия может быть как положительной, так и отрицательной.
Изменение кинетической энергии всегда равно работе действующих на тело сил, а изменение потенциальной энергии равно (со знаком «минус») работе только консервативных сил (но не сил трения, зависящих от скорости)
И потенциальная и кинетическая энергии являются функциями состояния системы, т. е. они точно определены, если известны координаты и скорости всех тел системы.
Слайд 33Закон сохранения энергии в механике
В замкнутой системе тел положительная работа внутренних
Слайд 34ΔЕк = Aт
ΔЕп = -Ат
ΔЕк = -ΔЕп.
Равенство означает, что увеличение кинетической энергии системы равно
ΔЕк + ΔЕп = 0
Δ (Ек + Еп) = 0
Изменение суммы кинетической и потенциальной энергий системы равно нулю.
Полная механическая энергия Е равна сумме кинетической и потенциальной энергий тел, входящих в систему:
Е = Ек + Еп = const.
Закон сохранения механической энергии (частный)
В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Слайд 35Общий закон сохранения энергии Энергия не создаётся и не уничтожается, а только
Слайд 36Сила трения совершает отрицательную работу и уменьшает кинетическую энергию. Но потенциальная
Уменьшение механической энергии системы под действием сил трения.
Но убывание механической энергии не означает, что эта энергия исчезает бесследно. Происходит переход энергии из механической формы в другие. При работе сил трения происходит нагревание тел, или увеличение их внутренней энергии.
Работа же силы сопротивления воздуха отрицательна как при подъёме тела вверх, так и при движении его вниз. Поэтому на замкнутом пути она обязательно меньше нуля.
Слайд 37Работа сил трения, действующих внутри системы, всегда отрицательна и механическая энергия
DE = Атр < 0
Слайд 38СТОЛКНОВЕНИЕ УПРУГИХ ШАРОВ
Применим закон сохранения энергии для нахождения скорости двух шаров
Под абсолютно упругим ударом понимают такой удар, при котором механическая энергия сохраняется
Если начальные скорости шаров направлены по линии, соединяющей их центры, то удар называют центральным.
Слайд 39Закон сохранения импульса в проекциях на ось Х будет иметь следующий
Закон сохранения энергии :
Разделив почленно второе уравнение на первое, получим: