- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме:Вектора. Действия над векторами
Содержание
- 1. Презентация по теме:Вектора. Действия над векторами
- 2. действия над векторами
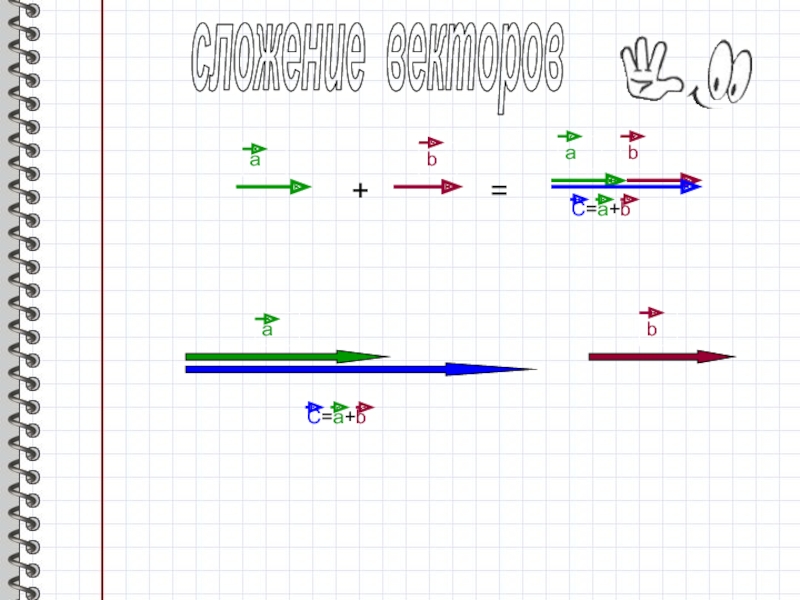
- 3. C=a+bааbb+=сложение вектороваbC=a+b
- 4. сложение вектороваbаbC=a+b+=аC=a+bb
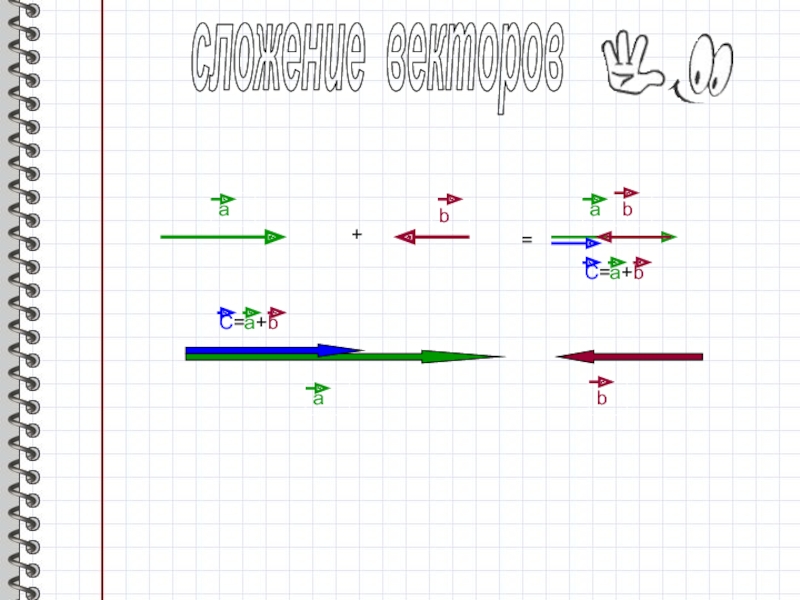
- 5. аb+=аbссложение векторовC=a+bbаСпособ 1: правило треугольника
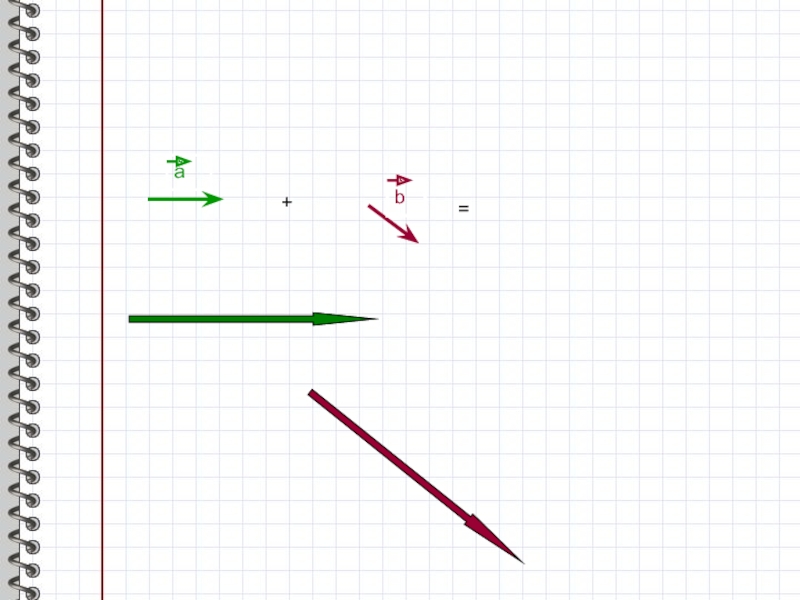
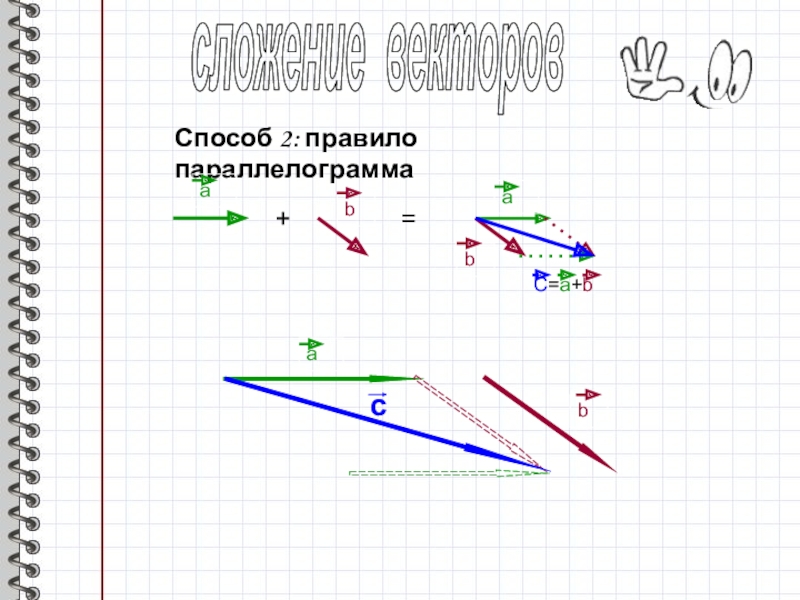
- 6. сложение векторовСпособ 2: правило параллелограммааbаbC=a+b+=аbс
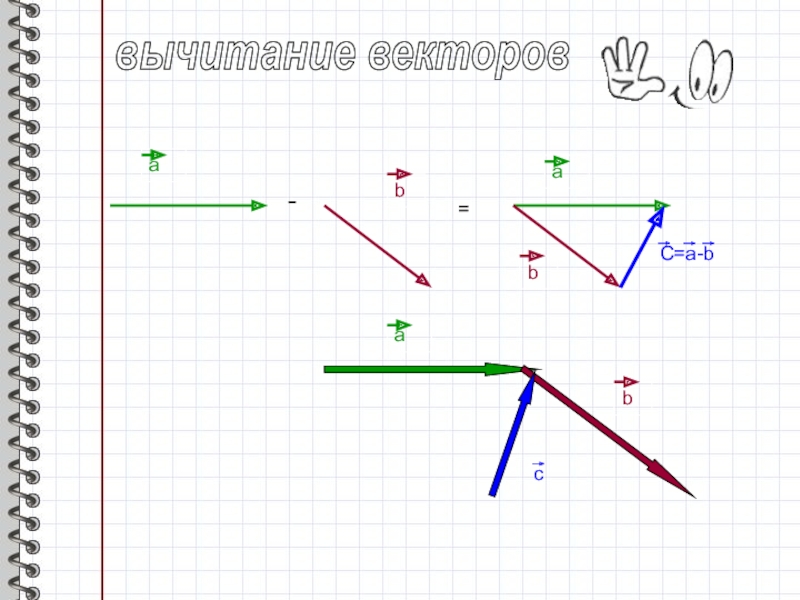
- 7. вычитание вектороваb-=аbС=а-bаbс
- 8. вычитание векторовсаb-аb=аbс
- 9. проекции вектораОдномерный случайхаах= а>0bсbx=0cx=0ddx=-d0ffx≠ffx
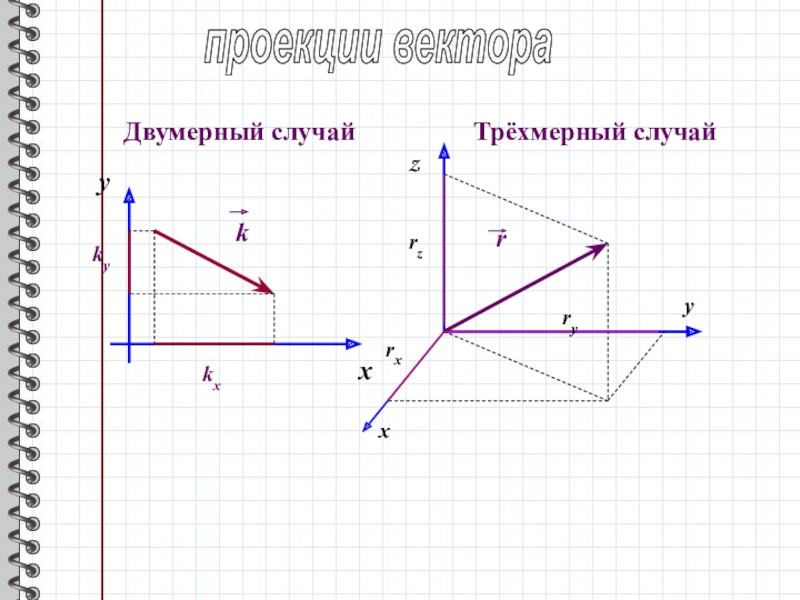
- 10. Двумерный случайТрёхмерный случайyxkkxkyzxyrrzrxryпроекции вектора
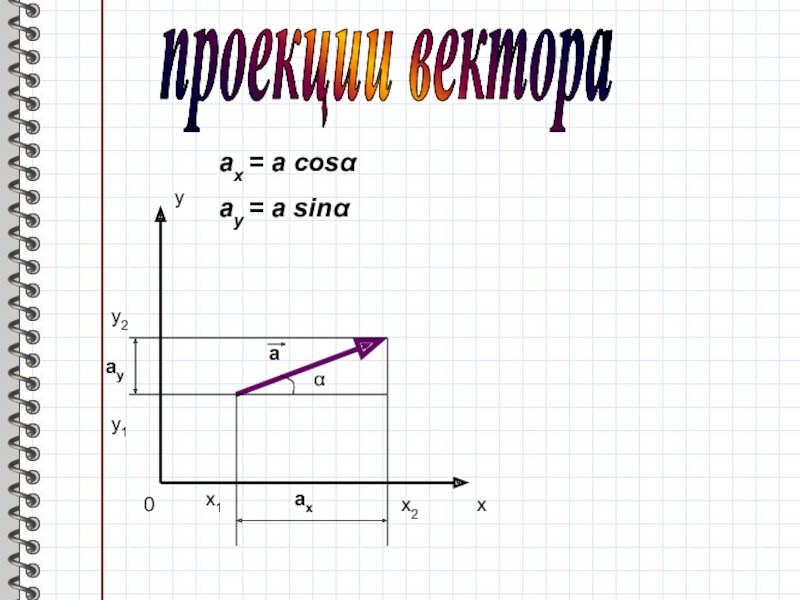
- 11. проекции вектораy1y2y0x1x2xαax = a cosαay = a sinαayaax
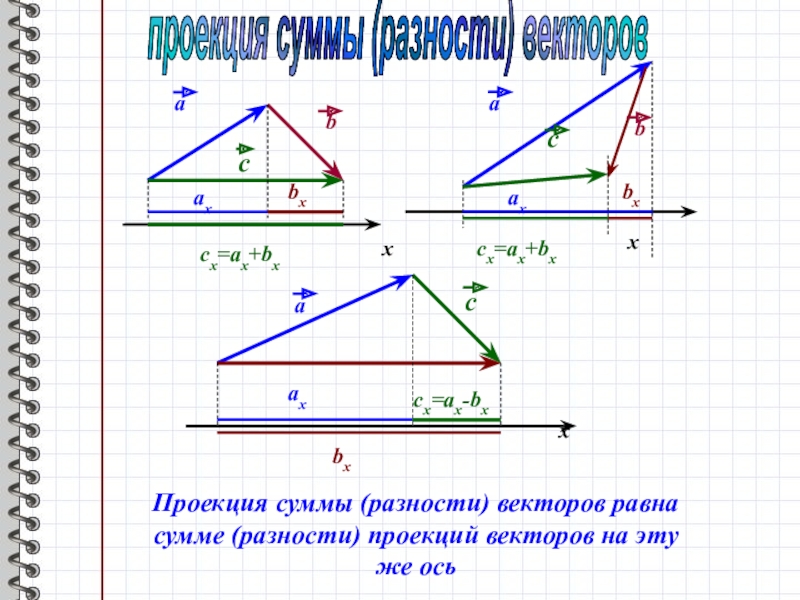
- 12. проекция суммы (разности) вектороваbсахbxcx=ax+bxxxасахbcx=ax+bxbxxахасcx=ax-bxbxПроекция суммы (разности) векторов равна сумме (разности) проекций векторов на эту же ось
- 13. Слайд 13
действия над векторами
Слайд 9проекции вектора
Одномерный случай
х
а
ах= а>0
b
с
bx=0
cx=0
d
dx=-d0
f
fx≠f
fx
к проекции конца нужно идти по направлению оси.
Слайд 12проекция суммы (разности) векторов
а
b
с
ах
bx
cx=ax+bx
x
x
а
с
ах
b
cx=ax+bx
bx
x
ах
а
с
cx=ax-bx
bx
Проекция суммы (разности) векторов равна сумме (разности) проекций
векторов на эту же ось