- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задачи повышенной сложности по геометрии
Содержание
- 1. Презентация по математике Задачи повышенной сложности по геометрии
- 2. Цели:1) Знакомство с нестандартными приёмами решения задач
- 3. Задача №1 Дан прямоугольник АВСD, в
- 4. Задача №2 Равнобедренный треугольник АВС с основанием
- 5. Задача№3 (олимпиада учителей 2010) Известно, что середины
- 6. Слайд 6
- 7. Слайд 7
- 8. Задача №5 (олимпиада учителей 2011) (Предложил
- 9. Задача №6 (олимпиада учителей 2011, А.В.
- 10. Задача №6 (олимпиада учителей 2011, А.В.
- 11. Задача №6 (олимпиада учителей 2011, А.В.
- 12. Задача №6 (олимпиада учителей 2011, А.В.
- 13. Задача №6 (олимпиада учителей 2011, А.В.
- 14. Задача №7 (олимпиада учителей 2008) Внутри треугольника
- 15. Задача №7 (олимпиада учителей 2008) Внутри треугольника
- 16. Задача №8 (ЕГЭ,С4) Две окружности касаются внешним
- 17. Список литературы: Методическое пособие по математике. Под
Слайд 1 Решение задач повышенной сложности и задач олимпиад по геометрии Презентация сделана Лопаткиной
Слайд 2
Цели:
1) Знакомство с нестандартными приёмами решения
задач планиметрии и стереометрии
2) Подготовка
3) Подготовка к экзамену ЕГЭ
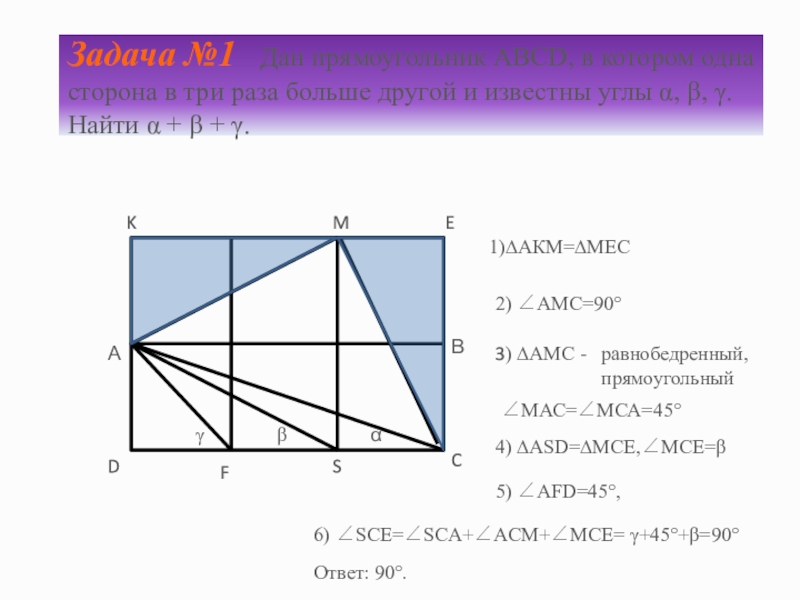
Слайд 3Задача №1 Дан прямоугольник АВСD, в котором одна сторона в
γ
β
А
В
D
C
K
E
M
1)∆АКМ=∆МЕС
2) АМС=
90°
3) ∆АМС -
равнобедренный, прямоугольный
МАС=МСА=45°
F
S
4) ∆ASD=∆MCE,MCE=β
5) AFD=45°,
6) SCE=SCA+ACM+MCE= γ+45°+β=90°
Ответ: 90°.
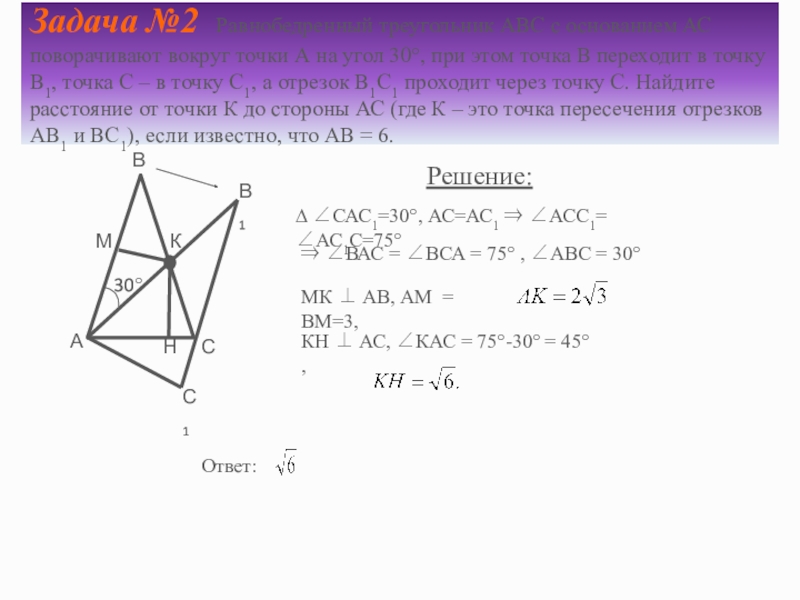
Слайд 4Задача №2 Равнобедренный треугольник АВС с основанием АС поворачивают вокруг точки
А
В
С
С1
В1
30°
К
М
Н
Решение:
∆ САС1=30°, АС=АС1 АСС1= АС1С=75°
ВАС = ВСА = 75° , АВС = 30°
МК АВ, АМ = ВМ=3,
КН АС, КАС = 75°-30° = 45° ,
Ответ:
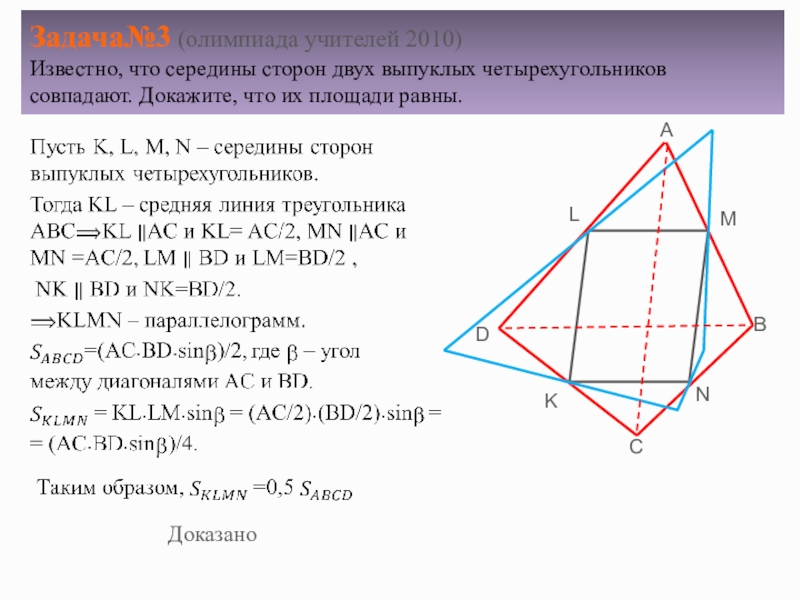
Слайд 5Задача№3 (олимпиада учителей 2010) Известно, что середины сторон двух выпуклых четырехугольников совпадают.
Доказано
K
L
M
N
A
B
C
D
Слайд 8 Задача №5 (олимпиада учителей 2011) (Предложил А.Г. Мякишев) Даны три попарно пересекающиеся
Ответ:
f
a
b
c
d
e
Проведем общие хорды АQ, BR и СР для каждой
пары окружностей . Прямые АQ, BR и СР являются
радикальными осями пар данных окружностей,
которые пересекаются в одной точке Т
(радикальном центре трех окружностей).
A
Q
B
R
C
P
СTR BTР⟹
АTР СTQ⟹
T
BTQ ~ ATR, т.к. BTQ = ATR (вертик.),
TВQ = TАR (вписанные углы, опирающиеся
на одну и ту же дугу)⟹
Перемножая почленно эти три равенства,
получим:
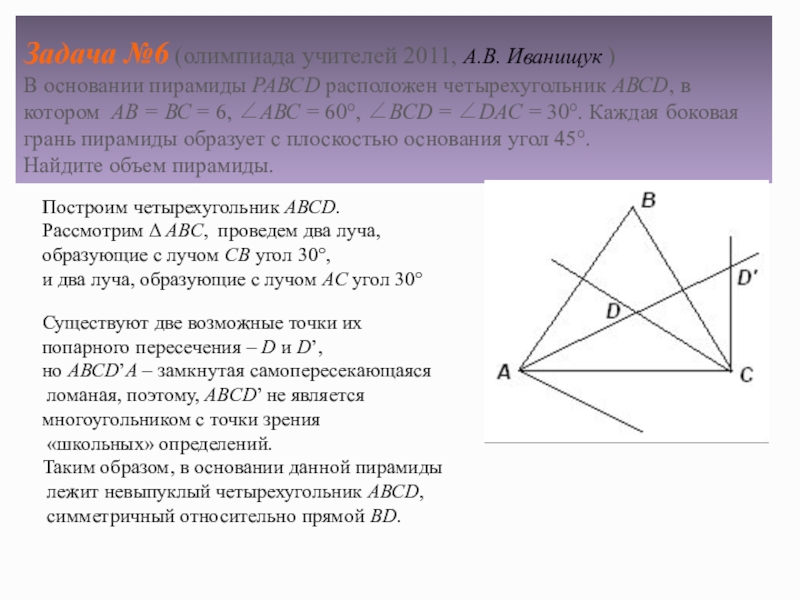
Слайд 9 Задача №6 (олимпиада учителей 2011, А.В. Иванищук ) В основании пирамиды РАВСD
Существуют две возможные точки их
попарного пересечения – D и D’,
но АВСD’A – замкнутая самопересекающаяся
ломаная, поэтому, АВСD’ не является
многоугольником с точки зрения
«школьных» определений.
Таким образом, в основании данной пирамиды
лежит невыпуклый четырехугольник АВСD,
симметричный относительно прямой BD.
Построим четырехугольник АВСD.
Рассмотрим АВС, проведем два луча,
образующие с лучом СВ угол 30,
и два луча, образующие с лучом АС угол 30
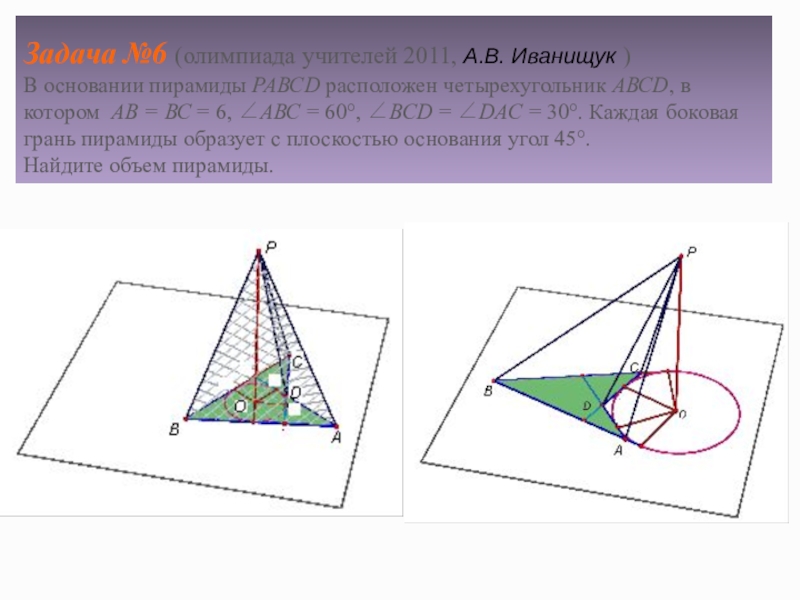
Слайд 10 Задача №6 (олимпиада учителей 2011, А.В. Иванищук ) В основании пирамиды РАВСD
Т.к. боковые грани данной пирамиды одинаково наклонены
к плоскости основания, то ортогональной проекцией
ее вершины Р на плоскость основания является точка О,
равноудаленная от прямых АВ, ВС, СD и DA.
Т. к. точка О должна лежать на луче BD –
биссектрисе угла АВС, а также на
биссектрисах углов А и С четырехугольника
(внутренних либо внешних),
то возможны два случая расположения
этой точки, которая будет являться
центром окружности,
касающейся четырех указанных
прямых.
Слайд 11 Задача №6 (олимпиада учителей 2011, А.В. Иванищук ) В основании пирамиды РАВСD
Слайд 12 Задача №6 (олимпиада учителей 2011, А.В. Иванищук ) В основании пирамиды РАВСD
.
Так как угол наклона боковых граней к основанию равен 45,
то высота Н пирамиды в каждом случае
равна радиусу r рассматриваемой окружности.
Слайд 13 Задача №6 (олимпиада учителей 2011, А.В. Иванищук ) В основании пирамиды РАВСD
OAN = 45⟹ NO =AN=0,5 AC = 3
MBO=30º, MOB=60º, ADO=60º, как внешний в ADB⟹DOK=30
K
MOK= MOB -DOK=60-30º =30º
AO –биссектриса MOK ⟹AOK=30:2=15
OAK=75,OAN= OAK- NAD=75-30=45
Слайд 14Задача №7 (олимпиада учителей 2008) Внутри треугольника расположены три окружности с радиусами
О
А
С
В
О
М
Q
P
T
D
Пусть OP=r, MQ=c, γ=А. MQ⊥AB, OP⊥AB.
PD=DT=QD⟹D – середина PQ.
AMQ~ADT ~AOP⟹ADT=AOP⟹
DQM~DTO; MDT+ODT=90º⟹
DT⊥AO, MDO=90
Слайд 15Задача №7 (олимпиада учителей 2008) Внутри треугольника расположены три окружности с радиусами
О
А
С
В
О
М
Q
P
T
D
ctg(ctg+ctg)=1- ctgctg
ctgctg+ ctgctg+ctgctg=1
При а=4, b=6,25, c=9 получим r=18,5
Ответ: 18,5
Слайд 16Задача №8 (ЕГЭ,С4) Две окружности касаются внешним образом. Найдите угол между двумя
А
F
Пусть NAQ=, OP⊥QN
Q
O
M
N
K
B
В ABC AK – биссектриса и высота ⟹AB=AC
OP∥AN⟹POQ=NAQ=
C
E
P
BC –внутренняя касательная, AF, AN – внешние. QK=QN=R, OK=OM=r
AQ – биссектриса А, OAQ, KAQ
Слайд 17Список литературы:
Методическое пособие по математике. Под ред. Шабунина М.И. - М.:
Р.К. Гордин “ Это должен знать каждый матшкольник “. М.: МЦНМО , 2006
В.В. Ткачук “ Математика – абитуриенту ” – М.: МЦНМО , 2008 , 1024 с.
Всероссийские олимпиады школьников по математике 1993 – 2006 .
Под ред. Н.Х. Агаханова М.: МЦНМО , 2007 , 472 с.
Сайт МФТИ www.mipt.ru
ЗФТШ при МФТИ http://www.school. mipt.ru/
Математические этюды http://www.etudes.ru