скорости движения
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Решение графических задач по кинематике и на нахождение средней скорости движения
Содержание
- 1. Презентация по физике на тему Решение графических задач по кинематике и на нахождение средней скорости движения
- 2. Задача№1:график зависимости координаты от времени На рисунке
- 3. Слайд 3
- 4. Тогда для первого, второго тела соответственно: x1=xо1+v1хt
- 5. Задача№ 2: встреча тел на графике движения
- 6. РешениеТак как изменение координаты тела происходит
- 7. б) Зная также, что v=tg α (геометрический смысл
- 8. Задача № 3: средняя скорость автомобиля и
- 9. Решение: Проанализируем условие задачи: первую половину пути автомобиль
- 10. Задача №4: средняя скорость автомобиля и две
- 11. Решение: В отличие от предыдущий задачи, автомобиль
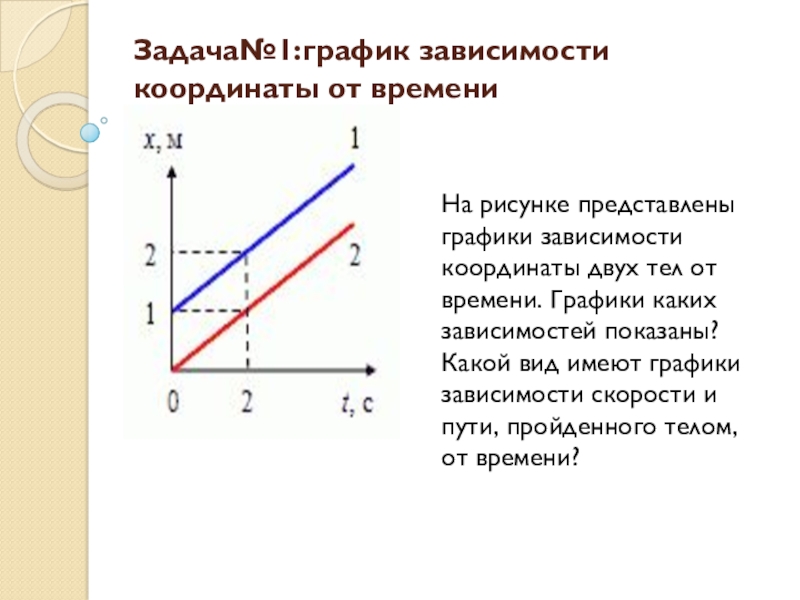
Задача№1:график зависимости координаты от времени На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути, пройденного телом, от времени?
Слайд 2Задача№1:график зависимости координаты от времени
На рисунке представлены графики зависимости координаты двух
тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути, пройденного телом, от времени?
Слайд 3
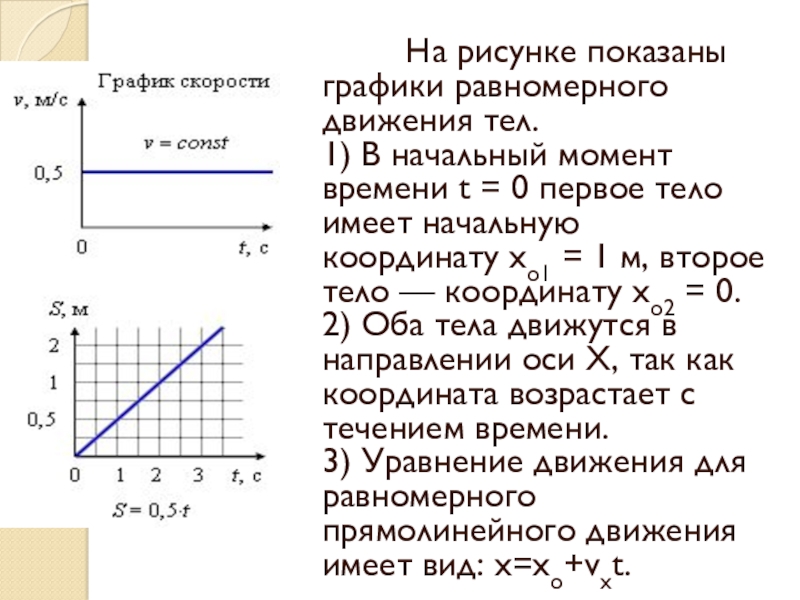
На рисунке показаны графики равномерного движения тел.
1) В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0.
2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени.
3) Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.
Слайд 4Тогда для первого, второго тела соответственно: x1=xо1+v1хt и x2=xо2+v2хt или x1=1+v1хt, x2=v2хt. Определим скорости первого
и второго тела:
v1x=x1 − 1=2 − 1= 0,5 м/с.t2v2x=x2=1= 0,5 м/с.t2Уравнения скорости имеют вид: v1х=v2х=0,5 м/с.
Так как S=vхt, то уравнение пути S=0,5t.
Слайд 5Задача№ 2: встреча тел на графике движения
Графики каких движений показаны на
рисунке? Как отличаются скорости движения этих тел? В какой момент времени тела встретились? Какие пути тела прошли до встречи?
Слайд 6
Решение
Так как изменение координаты тела происходит прямо пропорционально времени, то можно
утверждать, что движение равномерное и прямолинейное. По отношению к точке отсчета (0; 0) у первого тела координата убывает, а у второго наоборот — возрастает. Первое тело движется против оси х, второе — по направлению оси координат.
а) Чтобы ответить на вопрос об отличии скоростей, определим их из уравнения координаты:vx=x − xo/t тогда
v1x=3 − 6м/с/4 = −0.75 м/с.
v2x=3 − 0м/с/ 4= 0.75 м/с.
Скорости тел равны по абсолютному значению, но противоположны по направлению.
v1x=3 − 6м/с/4 = −0.75 м/с.
v2x=3 − 0м/с/ 4= 0.75 м/с.
Скорости тел равны по абсолютному значению, но противоположны по направлению.
Слайд 7 б) Зная также, что v=tg α (геометрический смысл скорости) и сравнивая углы наклонов
графиков движения тел к оси t, приходим к выводу, что углы одинаковы, следовательно, скорости равны.
в) Точка пересечения двух прямых означает, что тела встретились в одно и то же время в одной и той же точке, т. е. время встречи t = 4 c, а координата x = 3 м.
г) Так как движение равномерное и прямолинейное, то S = x − xo. Находим пути, пройденные телами до встречи:
S1= | x1 − xo1 | = | (3−6) м | = 3 м,
S2= | x2 − xo2 | = | (3−0) м | = 3 м.
Оба тела, двигаясь с одинаковыми скоростями, за одно и тоже время прошли равное расстояние.
Слайд 8Задача № 3: средняя скорость автомобиля и две половины пути
Первую половину
пути автомобиль проехал со средней скоростью v1 = 60 км/ч, а вторую — со средней скоростью v2 = 40 км/ч. Определить среднюю скорость автомобиля на всем пути.
Слайд 9Решение:
Проанализируем условие задачи: первую половину пути автомобиль проехал со скоростью 60
км/ч и затратил время, равноеt1=S/2 .v1 Вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время, равноеt2=S/2 .v2 По определению, средняя скорость V при равномерном прямолинейном движении равна отношению всего пройденного пути ко всему затраченному времени.
Подставляя значения скорости в формулу средней скорости, получим: V=2 • 60 • 40/60 + 40
скорость равна 48 км/ч.
Подставляя значения скорости в формулу средней скорости, получим: V=2 • 60 • 40/60 + 40
скорость равна 48 км/ч.
Слайд 10Задача №4: средняя скорость автомобиля и две половины времени
Первую половину времени
автомобиль двигался со средней скоростью v1 = 40 км/ч, а вторую — со средней скоростью v2 = 60 км/ч. Определить среднюю скорость автомобиля на всем пути.
Слайд 11Решение:
В отличие от предыдущий задачи, автомобиль движется первую половину времени с
одной скоростью 40 км/ч, а вторую половину времени — со скоростью 60 км/ч. Следовательно, автомобиль проходит за равные промежутки времени разные расстояния.S1=v1t/2иS2=v2t/2тогда средняя скорость
V =S1 + S2=(v1t/2 + v2t/2)/t=(v1 + v2)/2.
Средняя скорость для этого случая оказалась равной среднему арифметическому значению скоростей. Подставим значения скоростей и проведем вычисления:V =(40 + 60)/2= 50 км/ч.Средняя скорость равна 50 км/ч
V =S1 + S2=(v1t/2 + v2t/2)/t=(v1 + v2)/2.
Средняя скорость для этого случая оказалась равной среднему арифметическому значению скоростей. Подставим значения скоростей и проведем вычисления:V =(40 + 60)/2= 50 км/ч.Средняя скорость равна 50 км/ч