- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Механика
Содержание
- 1. Презентация по физике на тему Механика
- 2. Задача. ( вар.4529 в.25)
- 3. Задача. ( вар.4513 в.25 )
- 4. Задача. ( вар.4519 в.24)
- 5. Задача. ( вар.4527 в.10)Из одного пункта в
- 6. Задача. ( вар.4516 в.25 )
- 7. Задача. ( вар.4511 в.19 )Два когерентных источника
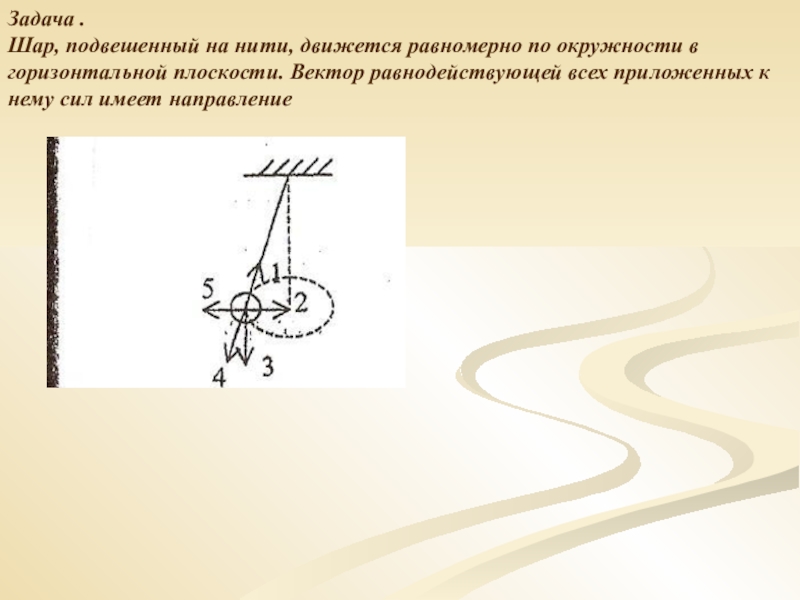
- 8. Задача .Шар, подвешенный на нити, движется равномерно
- 9. Задача.Равнодействующая сил, действующих на тело, равна нулю
- 10. Задача .На рисунке представлен график зависимости силы,
- 11. Задача:Пробка объемом V плавает на поверхности керосина.
- 12. Задача. ( вар.4511 в.11)Масса лодки вместе
- 13. Задача.Металлический брусок помещают в жидкость (рис). Выталкивающие
- 14. Задача Минимальная сила, для равномерного подъёма тела
- 15. Задача. (вар.4528 в.20)Чтобы при подъеме груза весом
- 16. Задача.С неподвижно висящего аэростата спускают железную проволоку.
- 17. Достаточно много задач на определение силы упругости,
- 18. ЗадачаЧасто встречаются задания, в которых нужно ответить
- 19. Задача.При подвешивании груз проволока удлинилась на 8
- 20. Задача Вес подвижного блока 10 Н .
- 21. Слайд 21
- 22. Задача
- 23. ЗадачаЧтобы вытащить гвоздь длиной 20см из доски
- 24. Задача.Для удлинения пружины на 4мм нужно совершить
- 25. Задача. Санки массой 7кг съезжают с горки
- 26. Задача. ( вар.4527 в.25)
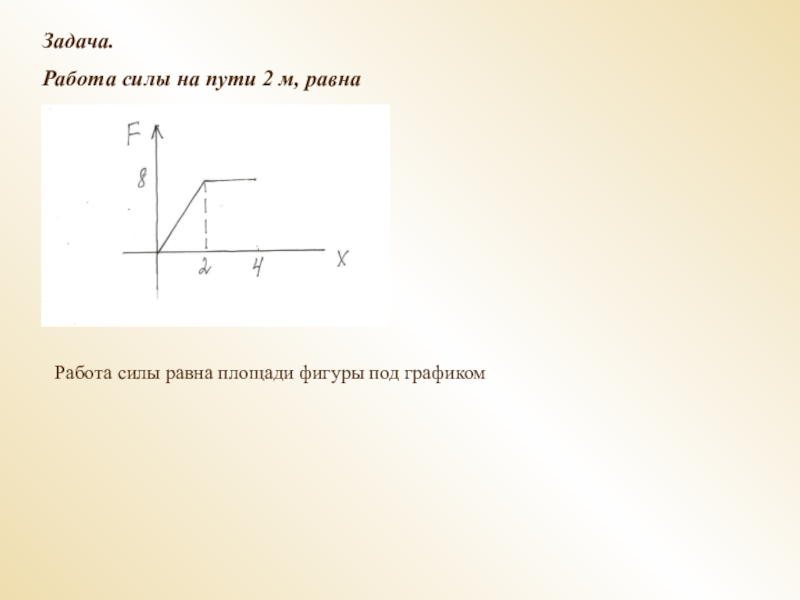
- 27. Задача. Работа силы на пути 2 м, равнаРабота силы равна площади фигуры под графиком
- 28. Задача Тело массой m движется равномерно по
- 29. Задача Стальной шар при подлете к упругой
- 30. Задача Из ствола пушки вылетает снаряд
- 31. Задача Ракета, масса которой без топлива 400
- 32. Задача. На доске длиной 4 м и
- 33. Спасибо за внимание! Удачи Вам! 4 ноября 2015 год
Слайд 2Задача. ( вар.4529 в.25)
Часовая и минутная
Центростремительное ускорение конца часовой стрелки в положении,
изображенном на рис.а, направлено по стрелке
Решение:
При равномерном движении по окружности центростремительное ускорение во
всех точках траектории направлено к центру. Часовая стрелка имеет меньшую
длину (т.е.9 часов), значит, направление ускорения 4
Слайд 3Задача. ( вар.4513 в.25 )
Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных
осей. Отношение периодов вращения шестерен равно 3. Радиус меньшей
шестерни равен 6 см. Радиус большей шестерни
Решение:
В точке касания шестерни имеют одинаковые линейные скорости
По условию задачи
Линейная скорость связана с периодом соотношением
В нашем случае
или
Тогда,
Слайд 4Задача. ( вар.4519 в.24)
На рисунке представлен график зависимости скорости автомобиля от
времени. Путь, пройденный автомобилем за 5 с, равен
Решение:
Путь можно найти двумя способами:
1) по формулам для перемещений различных видов движения
2) геометрический способ- пройденный путь равен площади фигуры под
графиком скорости
По данному рисунку видим, что это трапеция, значит,
Слайд 5Задача. ( вар.4527 в.10)
Из одного пункта в одном направлении движутся автомобиль
со скоростью 40 м/с и почтовый голубь со скоростью 57,6 км/ч.
Голубь … автомобиль, т.к.его скорость…
Решение:
Чтобы ответить на этот вопрос, переведем скорость голубя в СИ
Ответ: голубь не догонит автомобиль, т.к. его скорость 16 м/с
Слайд 6Задача. ( вар.4516 в.25 )
Материальная точка начала равномерное движение со скоростью 1м/с из
точки А, являющейся вершиной равностороннего треугольника АВС,
со стороной 100 см. Пройденный путь за 2 с отличается от перемещения
за то же время
Решение:
Длина стороны 100 см=1м, значит, за 1 с точка проходит одну из сторон.
Через 2 с она окажется в точке С, тогда пройденный путь АВ+ВС=1+1=2м ,
а перемещение АС=1м.
Пройденный путь и перемещение отличаются в 2/1=2 раза
Слайд 7Задача. ( вар.4511 в.19 )
Два когерентных источника колеблются в одинаковых фазах
ν= 600 Гц. Скорость распространения колебаний в среде υ= 1,2 км/с.
Максимальное усиление колебаний будет наблюдаться при наименьшей
разности хода, равной
Решение:
Наблюдается условие интерференции
Условие максимума для интерференции
Наименьшая разность хода будет для k=1, поэтому
Слайд 8Задача .
Шар, подвешенный на нити, движется равномерно по окружности в
горизонтальной
нему сил имеет направление
Слайд 9Задача.
Равнодействующая сил, действующих на тело, равна нулю в промежутке
времени
Решение:
Так как
значит, ускорение а = 0 , т.е. скорость не меняется .
скорость постоянна в промежутке от t1 до t2
Слайд 10Задача .
На рисунке представлен график зависимости силы, действующей на тело, от
времени движения. В промежутке времени 2- 4 с
Решение:
В промежутке времени 2- 4с сила остается постоянной. По второму закону
Ньютона
масса не меняется, значит и ускорение не меняется.
Движение равноускоренное.
Слайд 11Задача:
Пробка объемом V плавает на поверхности керосина. В керосин погружена
часть
(плотность пробки 200кг/ м3, плотность керосина 800кг/ м3)
Решение:
Заданный вопрос:
1). Тело плотностью ρ плавает в жидкости плотностью ρ0.
в жидкость погружена часть тела
2). Судно погружено в воду до ватерлинии, вытесняет воду объемом 15000 м3.
Вес судна 5·107Н,тогда вес груза (ρ =103кг/м3)
Т.к.судно плавает, то
Тело плавает, поэтому Fтяж = Fвыт
Слайд 12Задача. ( вар.4511 в.11)
Масса лодки вместе с сидящими в ней
находится на плаву, то она вытесняет объем воды, равный
( ρв= 1000 кг/м3 )
Решение:
Т.к.лодка плавает, то
Тогда,
Слайд 13Задача.
Металлический брусок помещают в жидкость (рис). Выталкивающие силы в
положения бруска
Решение:
Выталкивающие или архимедовы силы зависят от рода жидкости и объема
погруженного в жидкость.
Бруски погружены в одну жидкость, значит, выталкивающая сила будет зависеть только от погруженного объема. В первом и втором случае бруски погружены полностью, значит, действующие на них выталкивающие силы одинаковы. В третьем случае погружена только часть бруска, поэтому, выталкивающая его сила будет меньше, чем в двух предыдущих случаях. F3
Слайд 14Задача
Минимальная сила, для равномерного подъёма тела по наклонной плоскости с
Решение:
Подъем равномерный, значит
Находим проекции на оси координат
На ОХ:
На ОУ:
Тогда,
Значит,
Слайд 15Задача. (вар.4528 в.20)
Чтобы при подъеме груза весом 43 кН напряжение в
не превышало 60 МПа, диаметр троса должен быть равен (π=3,14)
Решение:
Механическое напряжение
Слайд 16Задача.
С неподвижно висящего аэростата спускают железную проволоку. Когда нижний конец проволоки
Решение.
Механическое напряжение
Разрыв происходит под действием силы тяжести
значит
Значит, длина оторвавшейся части
Тогда аэростат находится на высоте
Слайд 17Достаточно много задач на определение силы упругости, сравнение жесткостей
пружин, на
определением общей жесткости двух соединенных пружин.
Задача
Груз массой m подвесили на двух пружинах k и 2k, соединенных
последовательно. В состоянии равновесия груз опустится на расстояние …
(пружины невесомы)
Решение.
Т.к. система находится в равновесии, то по I закону Ньютона Fупр = Fтяж .
Учитывая, что Fупр = kобщ · х и Fтяж = mg, получаем
kобщ · х = mg
Найдем жесткость системы. При последовательном соединении
Тогда
Примечание При последовательном соединении пружин:
При параллельном соединении пружин:
Слайд 18Задача
Часто встречаются задания, в которых нужно ответить на вопрос:
как изменится
длину или площадь поперечного сечения проволоки.
Решение:
По закону Гука с одной стороны: F =k Δl ,
с другой стороны: при малых деформациях σ = Е · ׀ε׀
по определению
;
тогда
, значит,
,т.к. F =k Δl , то
Т.е.жесткость прямо пропорциональна площади поперечного сечения и
обратно пропорциональна начальной длине, и не зависит от удлинения
Слайд 19Задача.
При подвешивании груз проволока удлинилась на 8 см.. При подвешивании
того
и в два раза большего радиуса, удлинение проволоки будет равно
Решение:
При подвешивании груза, в состоянии покоя
В данном случае
Левые части выражений равны, значит и правые тоже
Проверим, как изменится жесткость проволоки
Радиус увеличился в 2 раза, значит, площадь увеличилась в 4 раза,
длина увеличилась в 2 раза
Значит,
Слайд 20Задача
Вес подвижного блока 10 Н . Если к свободному концу
усилие 105 Н, то с помощью этого блока можно поднять груз массой ...
Решение.
Подвижный блок дает выигрыш в силе в 2 раза, но блок имеет массу, поэтому
F = F1·2 – P = 105 · 2 – 10 = 200 Н,
значит
кг
Задача
Длина наклонной плоскости 1 м, высота 0,6 м, коэффициент трения при
равномерном движении тела по плоскости к вершине равен 0,1.
КПД наклонной плоскости равен…
l
h
х
КПД наклонной плоскости можно найти по формуле
, где
Решение
Слайд 22
Задача
Автомобиль массой 1,3 т первые 75 м пути проходит за 10 с при
коэффициенте сопротивления движению 0,05. Работа двигателя автомобиля
равна
Решение:
Работа в данном случае м.б.определена
По второму закону Ньютона
Определим проекцию на ось Ох, направленную вдоль движения
Найдем ускорение и силу сопротивления
,
;
Слайд 23Задача
Чтобы вытащить гвоздь длиной 20см из доски надо приложить силу 500Н.
Считая, что сила взаимодействия гвоздя с материалом доски пропорциональна погруженной в доску части гвоздя, найти минимальную работу, совершенную при забивании гвоздя (силой тяжести гвоздя пренебречь).
Решение:
Задача:
Однородный стержень длиной 2м и массой 1кг лежит на земле. Какую
работу нужно совершить, чтобы поднять его в вертикальное положение?
Решение:
Т.к. стержень имеет распределение массы, то переходим к работе с центром массы, который находится в середине стержня, поэтому работа определяется по формуле
Слайд 24Задача.
Для удлинения пружины на 4мм нужно совершить работу 0.02Дж.
Для удлинения
Решение:
Можно решать непосредственно по формуле
Из первого условия найти жесткость пружины
и далее найти работу по второму условию.
А можно по формуле
через сравнение:
в 10 раз больше
=> А увеличивается в
раз, значит
А2= 100А1= 2 Дж.
Слайд 25Задача.
Санки массой 7кг съезжают с горки высотой 5м и у
Решение:
При спуске на преодоление трения затрачивается 350-100=250Дж;
Значит 350+250=600Дж
Потенциальная энергия тела на высоте
Слайд 26Задача. ( вар.4527 в.25)
На трех одинаковых упругих пружинах совершают незатухающие колебания
три тела. Полные механические энергии этих тел находятся в соотношении
Решение:
Полная механическая энергия в замкнутой системе равна максимальным
значениям кинетической и потенциальной энергий.
Для пружинного маятника
Значит, чем больше амплитуда, тем больше энергия, т.е.на рис.2
Слайд 28
Задача
Тело массой m движется равномерно по окружности с линейной скоростью
Найти изменение импульса тела через:
а) половину периода (или через полоборота);
б) период (или через один оборот).
Решение.
Изменение импульса тела
а) Через половину периода тело оказывается в диаметрально
противоположной точке, поэтому направление линейной
скорости меняется на противоположное, значит
Δр = mv – (-mv) = 2mv.
б) Через период тело возвращается в начальное положение,
поэтому направления линейной скорости в начальный и
конечный моменты времени совпадают, значит
Δр = mv – mv = 0.
Слайд 29Задача
Стальной шар при подлете к упругой стене имел импульс р0
После удара, который длился 0,001 с, импульс шарика стал
Модуль средней силы, с которой стенка подействовала на шарик, равен …
Решение.
Импульс силы равен изменению импульса тела:
Т.к. удар абсолютно упругий, то по закону сохранения
импульса, изменение импульса стены равно изменению
импульса шара, значит Δр = 2р0
(изменение импульса шара р0 – (-р0) = 2р0).
Значит F = Δр/t , F =2р0 /t = 2·0,5/ 0.001 = 1000 H
Слайд 30 Задача
Из ствола пушки вылетает снаряд под углом 60º к
80 м/с относительно Земли. Если масса снаряда 20 кг, а масса пушки 5 т,
то скорость отдачи пушки …
Решение
По закону сохранения импульса
Т.к. до выстрела пушка и снаряд покоились, то их
скорости v1п = v1с = 0. Тогда
Пушка откатывается по горизонтали, поэтому рассматриваем проекцию
только на ось ОХ: 0 = -mп vп + mс vс ·cosα , mп vп = mс vс ·cosα ,
Получаем
Слайд 31
Задача
Ракета, масса которой без топлива 400 г, при сгорании топлива
на высоту 125 м. Масса топлива 50 г. Если сгорание топлива происходит
мгновенно, то скорость выхода газов
Решение:
По закону сохранения импульса
Скорость ракеты найдем по закону сохранения энергии
Значит,
Находим скорость газа
Слайд 32Задача.
На доске длиной 4 м и массой 30 кг качаются
Где должна быть у доски точка опоры ( относительно первого мальчика,
сидящего слева), если они сидят на концах доски?
Решение:
Пусть m = 30кг- масса доски,
m1=30кг- масса мальчика,
сидящего слева,
m2= 40кг- масса второго мальчика,
х- расстояние от точки опоры до центра тяжести, l- длина доски.
Запишем условие равновесия рычага:
Значит, расстояние
;
;
;
;
;