- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике на тему Дифракция света (11 класс)
Содержание
- 1. Презентация по физике на тему Дифракция света (11 класс)
- 2. ЦЕЛЬ УРОКАобразовательная - расширить знания учащихся о
- 3. Выявление имеющихся знаний, умений и навыков Что
- 4. На прошлом уроке вы наблюдали кольца Ньютона
- 5. Выявление имеющихся знаний, умений и навыковПо какой
- 6. Определение дифракции светаДифракция света – это явление
- 7. Исторические сведения дифракцииПервое научное описание явления, в
- 8. Дифракция света. Опыт ЮнгаПервое качественное объяснение явления
- 9. Исторические сведения дифракции Французский ученый О.
- 10. Зоны ФренеляДля облегчения расчета Френель предложил разбить
- 11. Модель. Зоны ФренеляЕсли изготовить непрозрачный экран, который
- 12. Модель. Зоны Френеля
- 13. Теория ФренеляСогласно теории Френеля общий характер дифракционной
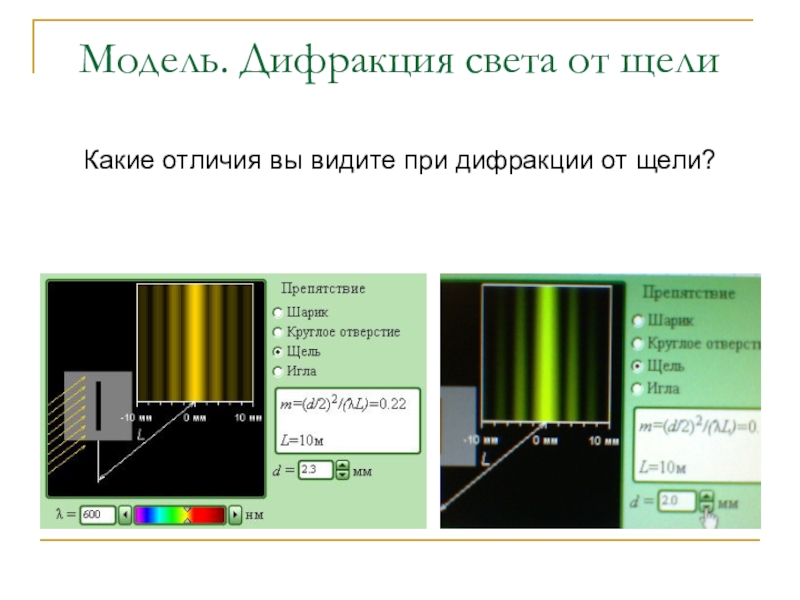
- 14. Модель. Дифракция света от щели Какие отличия вы видите при дифракции от щели?
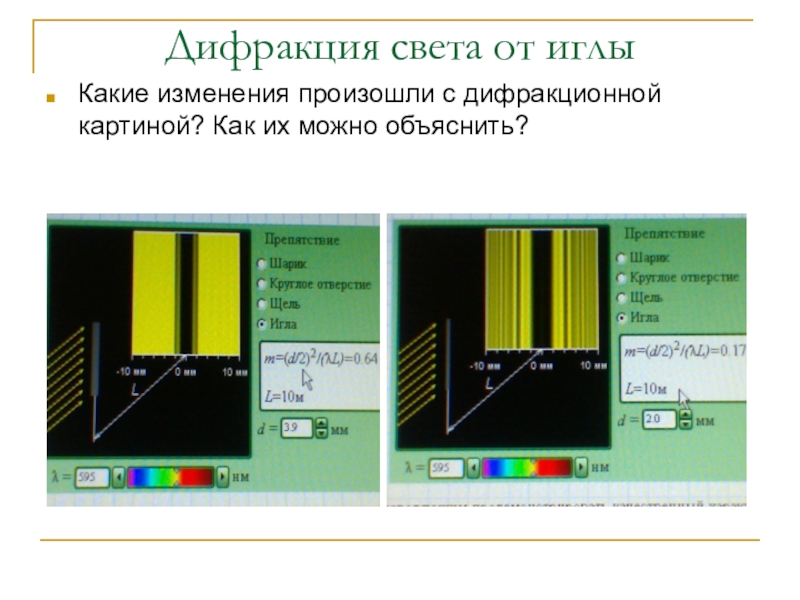
- 15. Дифракция света от иглыКакие изменения произошли с
- 16. Дифракция света на отверстииКак можно объяснить полученные дифракционные картины?
- 17. Дифракция света на шарикеКакие особенности выявлены при
- 18. Обратите внимание, что при дифракции на шарике
- 19. Теория ФренеляПри дифракции света на круглом диске
- 20. Теория ФренеляЕсли диск закрывает зоны не слишком
- 21. Проведение эксперимента для получения дифракционной картины от
- 22. Закрепление нового материалаКакое явление мы называем дифракцией
ЦЕЛЬ УРОКАобразовательная - расширить знания учащихся о природе света, раскрыть сущность физического явления - дифракции света с точки зрения электромагнитной теории; развивающая - создать условия для исследовательской деятельности учащихся, развить умение проводить эксперимент и делать выводы
Слайд 2ЦЕЛЬ УРОКА
образовательная - расширить знания учащихся о природе света, раскрыть сущность
физического явления - дифракции света с точки зрения электромагнитной теории;
развивающая - создать условия для исследовательской деятельности учащихся, развить умение проводить эксперимент и делать выводы из полученных результатов; развитие коммуникативных навыков
развивающая - создать условия для исследовательской деятельности учащихся, развить умение проводить эксперимент и делать выводы из полученных результатов; развитие коммуникативных навыков
Слайд 3Выявление имеющихся знаний, умений и навыков
Что такое интерференция?
Какой вид имеет
интерференционная картина?
При каком условии амплитуда колебаний частиц среды в данной точке максимальна?
Каково условие минимума амплитуды результирующих колебаний?
Какие волны дают устойчивую интерференционную картину?
Почему возникают радужные пятна на поверхности воды?
Объясните с помощью рисунка интерференцию в тонких пленках.
При каком условии амплитуда колебаний частиц среды в данной точке максимальна?
Каково условие минимума амплитуды результирующих колебаний?
Какие волны дают устойчивую интерференционную картину?
Почему возникают радужные пятна на поверхности воды?
Объясните с помощью рисунка интерференцию в тонких пленках.
Слайд 4
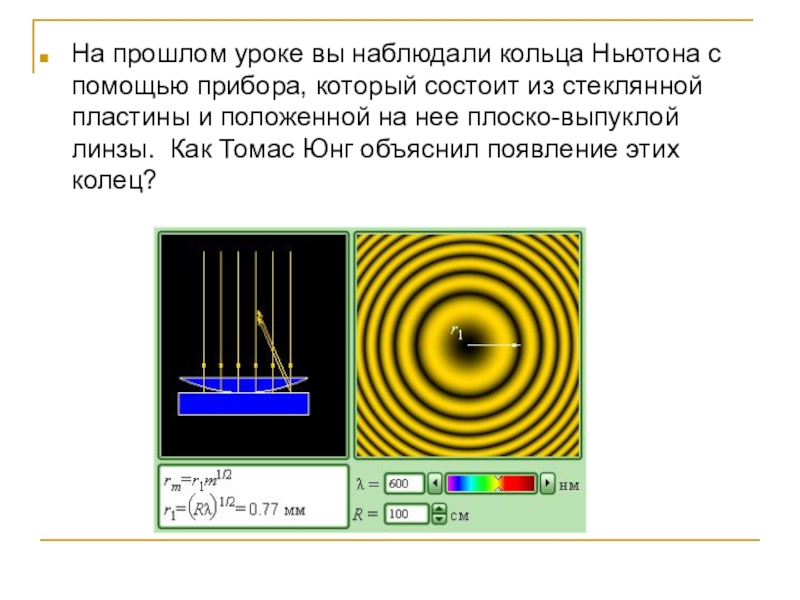
На прошлом уроке вы наблюдали кольца Ньютона с помощью прибора, который
состоит из стеклянной пластины и положенной на нее плоско-выпуклой линзы. Как Томас Юнг объяснил появление этих колец?
Слайд 5Выявление имеющихся знаний, умений и навыков
По какой формуле можно вычислить расстояние
до 2-го максимума?
Какой смысл имеет термин «просветление оптики»?
Назовите несколько применений интерференции
Какой смысл имеет термин «просветление оптики»?
Назовите несколько применений интерференции
Слайд 6Определение дифракции света
Дифракция света – это явление огибания светом препятствия и
и его проникновение в область геометрической тени.
Слайд 7Исторические сведения дифракции
Первое научное описание явления, в котором наблюдалось отклонение света
от прямолинейного направления, было дано в книге итальянского ученого Франческо Гримальди, опубликованной в 1665 г. Гримальди обнаружил, что тень от непрозрачного предмета оказалась шире, чем она должна быть при прямолинейном распространении света. Кроме того, по краям тени он наблюдал цветные полосы. Это явление он назвал дифракцией света.
Слайд 8Дифракция света. Опыт Юнга
Первое качественное объяснение явления дифракции на основе волновых
представлений было дано английским ученым Т. Юнгом(1802 г.).
Слайд 9Исторические сведения дифракции
Французский ученый О. Френель развил количественную теорию
дифракционных явлений (1818 г.)
Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом
Гипотезу Гюйгенса об огибающей вторичных волн Френель заменил физически ясным положением, согласно которому вторичные волны, приходя в точку наблюдения, интерферируют друг с другом
Слайд 10Зоны Френеля
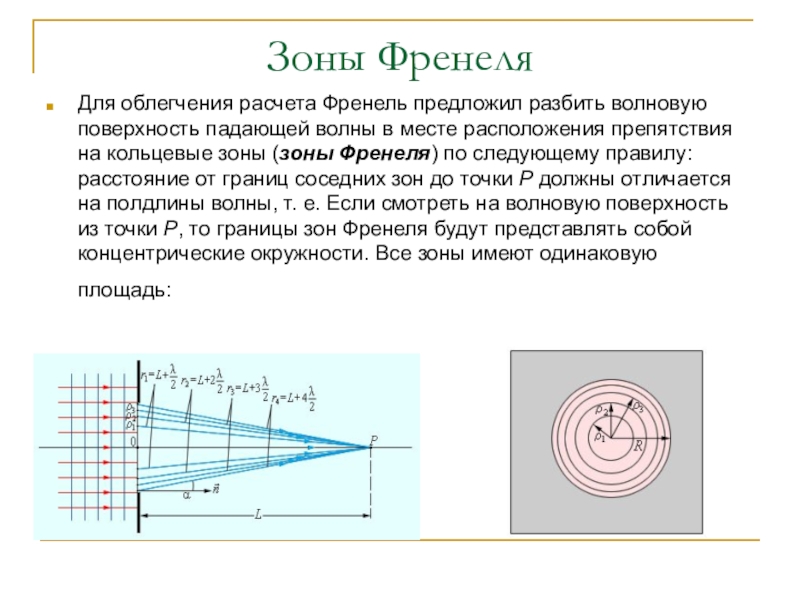
Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны
в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на полдлины волны, т. е. Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности. Все зоны имеют одинаковую площадь:
Слайд 11Модель. Зоны Френеля
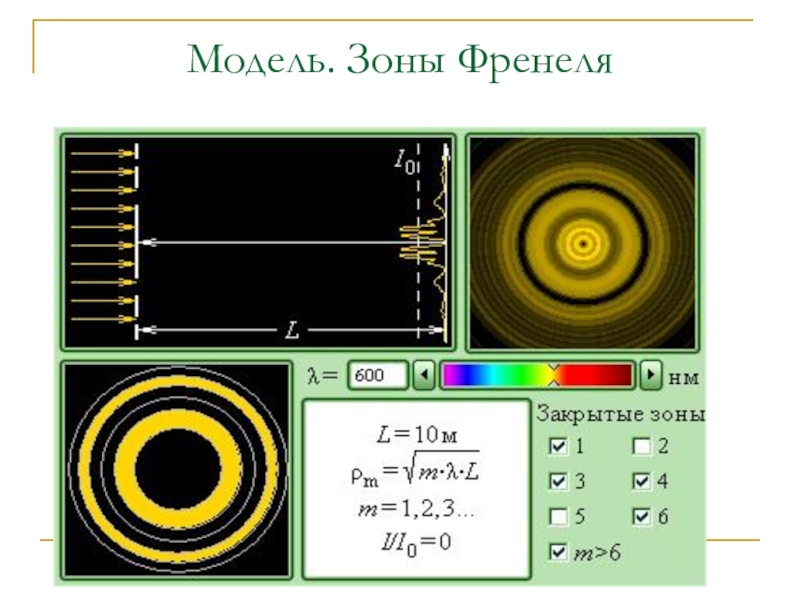
Если изготовить непрозрачный экран, который оставлял бы открытыми только
несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастает. Например, если открыты 1, 3 и 5 зоны, то A = 6A0, I = 36I0 В центре светлое пятно.
Что мы наблюдаем, если закрыты1, 2 и все зоны при m>6?
Что мы наблюдаем, если закрыты1, 2 и все зоны при m>6?
Слайд 13Теория Френеля
Согласно теории Френеля общий характер дифракционной картины зависит от безразмерного
параметра m, равного числу кольцевых зон Френеля, укладывающихся на радиусе круглого препятствия
m = R2 / (λL),
или числу полоскообразных зон Френеля, укладывающихся на полуширине линейного препятствия m = (0,5d)2/(λL).
или числу полоскообразных зон Френеля, укладывающихся на полуширине линейного препятствия m = (0,5d)2/(λL).
Слайд 15Дифракция света от иглы
Какие изменения произошли с дифракционной картиной? Как их
можно объяснить?
Диаметр 3,9 мм Диаметр 2 мм
Диаметр 3,9 мм Диаметр 2 мм
Слайд 18
Обратите внимание, что при дифракции на шарике в центре дифракционной картины
всегда наблюдается светлое пятно (пятно Пуассона), а при дифракции на круглом отверстии светлое пятно в центре возникает при целых нечетных значениях числа m, в то время, как при четных значениях числа m в центре картины наблюдается темное пятно.
Слайд 19Теория Френеля
При дифракции света на круглом диске закрытыми оказываются зоны Френеля
первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна
или A = Am+1/2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то Am+1 ≈ 2A0 и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
или A = Am+1/2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то Am+1 ≈ 2A0 и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
Слайд 20Теория Френеля
Если диск закрывает зоны не слишком больших номеров, то Am+1 ≈ 2A0
и A ≈ A0, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.
Слайд 21Проведение эксперимента для получения дифракционной картины от различных препятствий
Оборудование: лазерная указка,
щель, тонкая проволочка, диафрагмы.
Получить чёткую дифракционную картину от различных препятствий
Получить чёткую дифракционную картину от различных препятствий
Слайд 22Закрепление нового материала
Какое явление мы называем дифракцией света?
Как строятся зоны Френеля?
Какие
условия должны выполняться, чтобы появилась дифракционная картина?
Как работает зонная пластинка Френеля?
Что показывают опыты с пропусканием света через отверстия различных размеров?
Что показывают опыты с пропусканием света через непрозрачный диск различных размеров?
Как работает зонная пластинка Френеля?
Что показывают опыты с пропусканием света через отверстия различных размеров?
Что показывают опыты с пропусканием света через непрозрачный диск различных размеров?