- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике лабораторная работа
Содержание
- 1. Презентация по физике лабораторная работа
- 2. Вариант 1 Цель: Определить ускорение
- 3. Ход работыСобираем установку по рисунку 178. (Наклон
- 4. Чертим в тетрадь таблицу 4:Измеряем расстояние s,
- 5. Вычисляем время t движения шарика, его ускорение
- 6. ВыводОпределили ускорение движения шарика и его мгновенную скорость перед ударом о цилиндр.
- 7. Вариант 2 Цель: убедиться в
- 8. Ход работы Задание 1 Убедимся в том,
- 9. Собираем установку в соответствии с рисунком 179,
- 10. Освободим бумажную ленту. измерим на ней расстояния
- 11. Вычислим отношения s₂/s₁, s₃/s₁, …, s₁₅/s₁, округлив
- 12. Результаты вычислений запишем в виде ряда отношений,
- 13. Задание 2 Из формулы s=at²/2 выразим a
- 14. Задание 3 По формуле ? = at
- 15. По полученным данным построим график зависимости модуля мгновенной скорости бруска от времени:
- 16. Задание 4 Построим график зависимости координаты х
- 17. Вывод:Убедились в равноускоренном характере движения бруска и определили его ускорение и мгновенную скорость.
Вариант 1 Цель: Определить ускорение движения шарика и его мгновенную скорость перед ударом о цилиндрЖелоб лабораторный металлический длиной 1,4 м;Шарик металлический диаметром 1,5 – 2 см;Цилиндр металлический;Метроном (один на весь класс);Лента измерительная;Кусок мела. Оборудование:
Слайд 2
Вариант 1
Цель:
Определить ускорение движения шарика и его мгновенную скорость перед
ударом о цилиндр
Желоб лабораторный металлический длиной 1,4 м;
Шарик металлический диаметром 1,5 – 2 см;
Цилиндр металлический;
Метроном (один на весь класс);
Лента измерительная;
Кусок мела.
Желоб лабораторный металлический длиной 1,4 м;
Шарик металлический диаметром 1,5 – 2 см;
Цилиндр металлический;
Метроном (один на весь класс);
Лента измерительная;
Кусок мела.
Оборудование:
Слайд 3Ход работы
Собираем установку по рисунку 178. (Наклон желоба должен быть таким,
чтобы шарик проходил всю длину желоба не менее чем за три удара метронома.)
Слайд 4Чертим в тетрадь таблицу 4:
Измеряем расстояние s, пройденное шариком за три
или четыре удара метронома. Результаты заносим в таблицу:
Слайд 5Вычисляем время t движения шарика, его ускорение и мгновенную скорость перед
ударом о цилиндр. Результат измерений заносим в таблицу 4 с учетом абсолютной погрешности, полагая
∆s= 5мм=5*10¯³ м;
∆t=1 с;
∆a=(2s∆t+t∆s)/t³;
∆?=a∆t + t∆a.
∆s= 5мм=5*10¯³ м;
∆t=1 с;
∆a=(2s∆t+t∆s)/t³;
∆?=a∆t + t∆a.
Слайд 7
Вариант 2
Цель:
убедиться в равноускоренном характере движения бруска и определить его
ускорение и мгновенную скорость.
Прибор для изучения движения тел;
Ленты из миллиметровой и копировальной бумаги длиной 300 мм и шириной 20 мм;
Штатив с муфтой и лапкой.
Прибор для изучения движения тел;
Ленты из миллиметровой и копировальной бумаги длиной 300 мм и шириной 20 мм;
Штатив с муфтой и лапкой.
Оборудование:
Слайд 8Ход работы
Задание 1
Убедимся в том, что брусок движется по наклонной плоскости
равноускоренно, подготовим в тетради таблицу 5 для записи результатов измерений и вычислений:
Слайд 9Собираем установку в соответствии с рисунком 179, а:
Включим в сеть, нажмем
кнопку 7, а затем освободим зажим 6, не отпуская кнопку 7 до конца движения бруска.
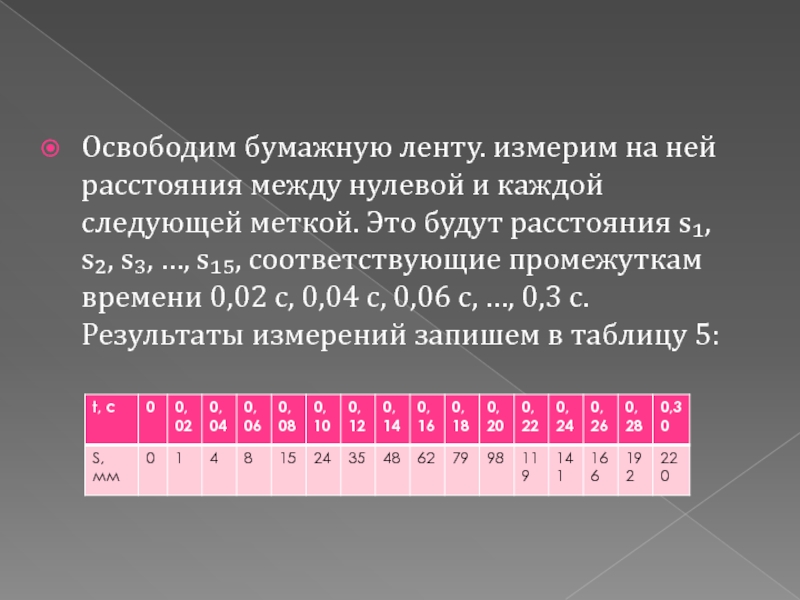
Слайд 10Освободим бумажную ленту. измерим на ней расстояния между нулевой и каждой
следующей меткой. Это будут расстояния s₁, s₂, s₃, …, s₁₅, соответствующие промежуткам времени 0,02 с, 0,04 с, 0,06 с, …, 0,3 с. Результаты измерений запишем в таблицу 5:
Слайд 11Вычислим отношения s₂/s₁, s₃/s₁, …, s₁₅/s₁, округлив результаты до целых чисел:
s₂/s₁=4
s₉/s₁=79
s₃/s₁=8 s₁₀/s₁=98
s₄/s₁=15 s₁₁/s₁=119
s₅/s₁=24 s₁₂/s₁=141
s₆/s₁=35 s₁₃/s₁=166
s₇/s₁=48 s₁₄/s₁=192
s₈/s₁=62 s₁₅/s₁=220
s₃/s₁=8 s₁₀/s₁=98
s₄/s₁=15 s₁₁/s₁=119
s₅/s₁=24 s₁₂/s₁=141
s₆/s₁=35 s₁₃/s₁=166
s₇/s₁=48 s₁₄/s₁=192
s₈/s₁=62 s₁₅/s₁=220
Слайд 12Результаты вычислений запишем в виде ряда отношений, дописав правую часть в
следующем уравнении:
s₁:s₂:s₃:s₄:s₅:s₆:s₇:s₈:s₉:s₁₀:s₁₁:s₁₂:s₁₃:s₁₄:s₁₅=1:2:3:4:5:6:7:8:9:10:11:12:13:14:15,
где под s₁ в данном случае подразумевается s₁/s₁=1, под s₂ - s₂/s₁ и т.д.
Вывод о характере движения бруска:
Полученные соотношения позволяют предположить, что брусок движется равноускоренно.
s₁:s₂:s₃:s₄:s₅:s₆:s₇:s₈:s₉:s₁₀:s₁₁:s₁₂:s₁₃:s₁₄:s₁₅=1:2:3:4:5:6:7:8:9:10:11:12:13:14:15,
где под s₁ в данном случае подразумевается s₁/s₁=1, под s₂ - s₂/s₁ и т.д.
Вывод о характере движения бруска:
Полученные соотношения позволяют предположить, что брусок движется равноускоренно.
Слайд 13Задание 2
Из формулы s=at²/2 выразим a через s и t:
a=2s/t²
Воспользовавшись полученными
экспериментальными данными, вычислим значение ускорения дважды (при t₁₀=0,2 с и соответствующем s₁₀ и при t₁₅=0,3 с и соответствующем s₁₅)
a₁₀=2s₁₀/t²₁₀=(2*0.098)/0.20²=4.9 м/с²
a₁₅=2s₁₅/t²₁₅=(2*0.22)/0.30²=4.88 м/с²
a₁₀=2s₁₀/t²₁₀=(2*0.098)/0.20²=4.9 м/с²
a₁₅=2s₁₅/t²₁₅=(2*0.22)/0.30²=4.88 м/с²
Слайд 14Задание 3
По формуле ? = at определим мгновенную скорость бруска к
концу промежутков времени 0,10, 0,20 и 0,30 от начала движения:
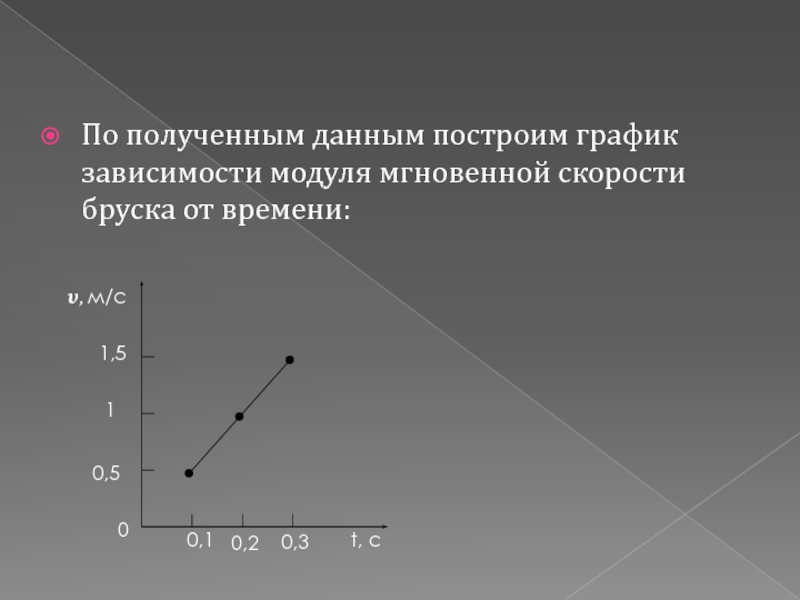
?₆ = a₆t₆ = 4,9*0,10 = 0,49 м/с
?₁₀ = a ₁₀t₁₀ = 4,9*0,20 = 0,98 м/с
?₁₅ = a₁₅t₁₅ = 4,9*0,30 = 1,47 м/с
?₆ = a₆t₆ = 4,9*0,10 = 0,49 м/с
?₁₀ = a ₁₀t₁₀ = 4,9*0,20 = 0,98 м/с
?₁₅ = a₁₅t₁₅ = 4,9*0,30 = 1,47 м/с
Слайд 15По полученным данным построим график зависимости модуля мгновенной скорости бруска от
времени:
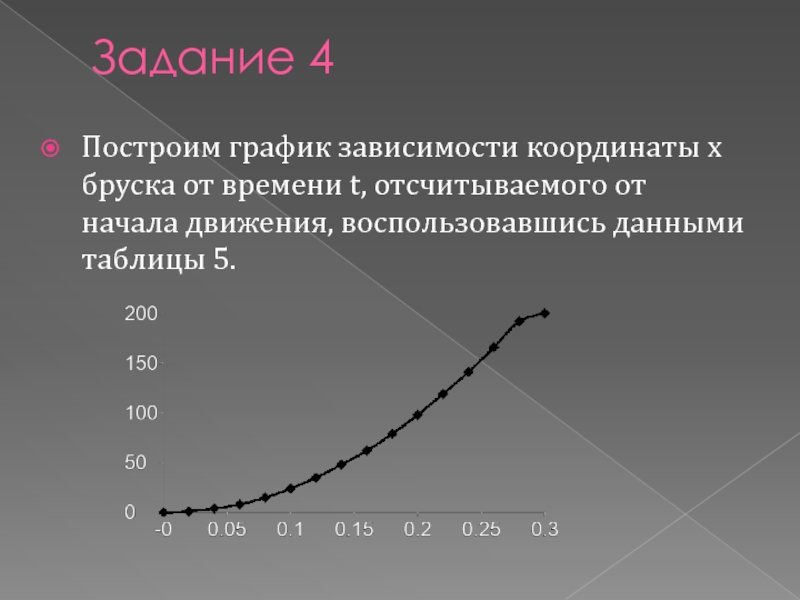
Слайд 16Задание 4
Построим график зависимости координаты х бруска от времени t, отсчитываемого
от начала движения, воспользовавшись данными таблицы 5.
Слайд 17Вывод:
Убедились в равноускоренном характере движения бруска и определили его ускорение и
мгновенную скорость.