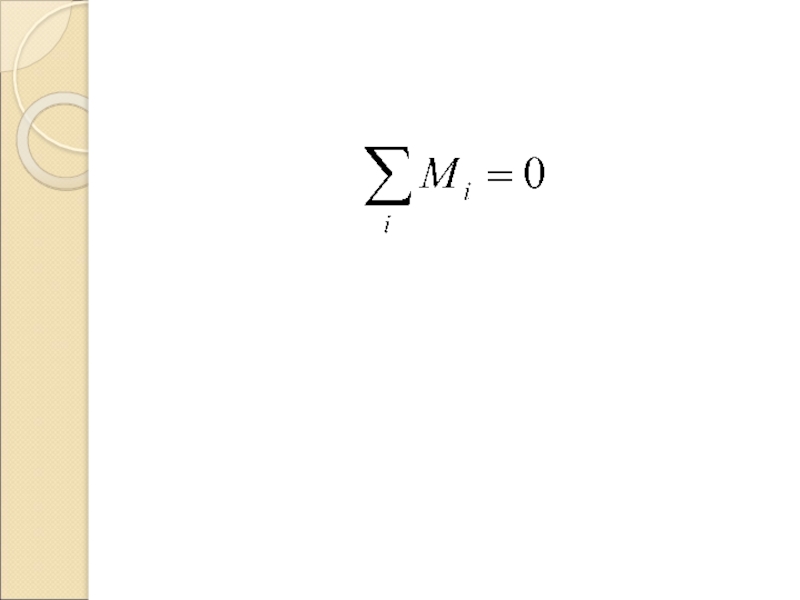- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике и астрономии Статика
Содержание
- 1. Презентация по физике и астрономии Статика
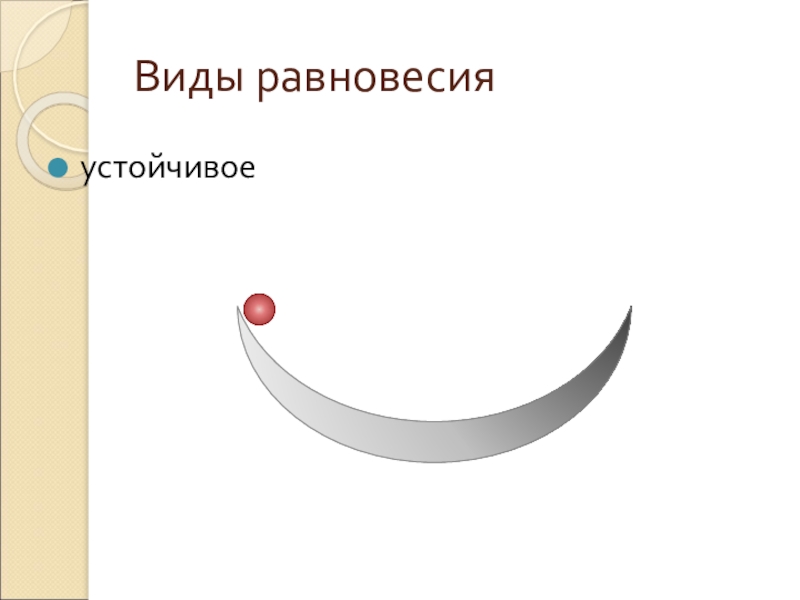
- 2. Виды равновесия
- 3. Виды равновесияустойчивое
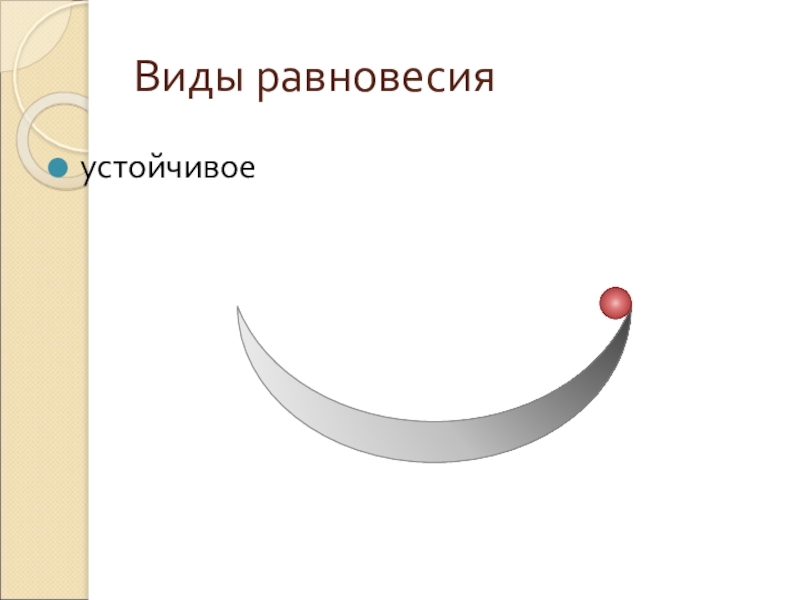
- 4. Виды равновесияустойчивое
- 5. Виды равновесияустойчивое
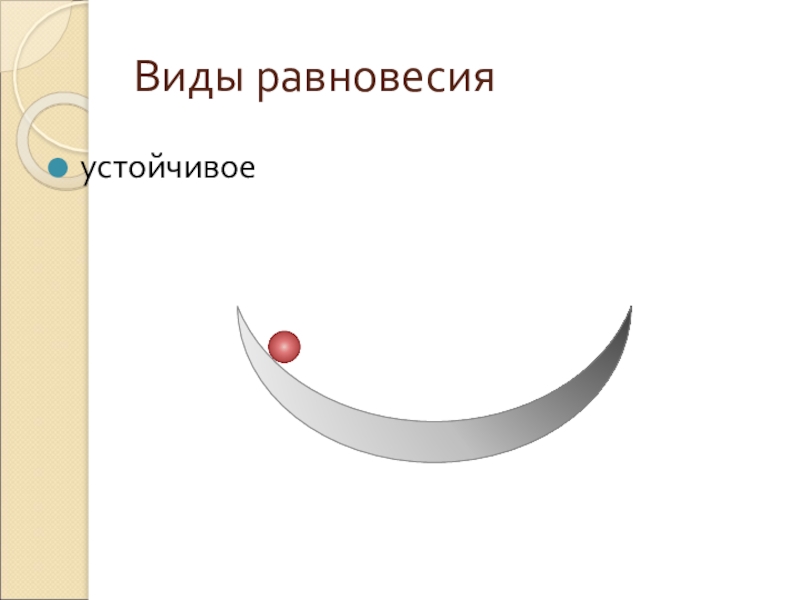
- 6. Виды равновесияустойчивое
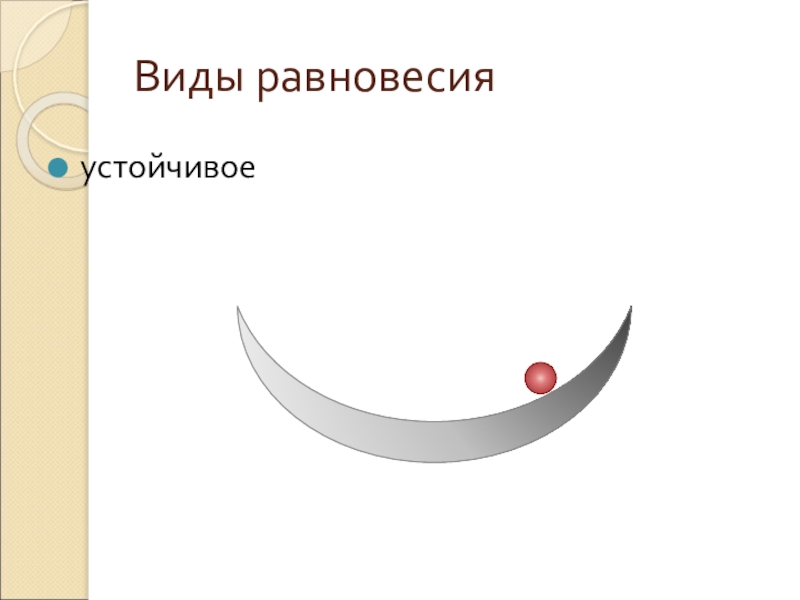
- 7. Виды равновесияустойчивое
- 8. Виды равновесияустойчивое
- 9. Виды равновесиянеустойчивое
- 10. Виды равновесиябезразличное
- 11. Виды равновесиябезразличноенеустойчивоеустойчивоеEп= maxEп= minEп= const
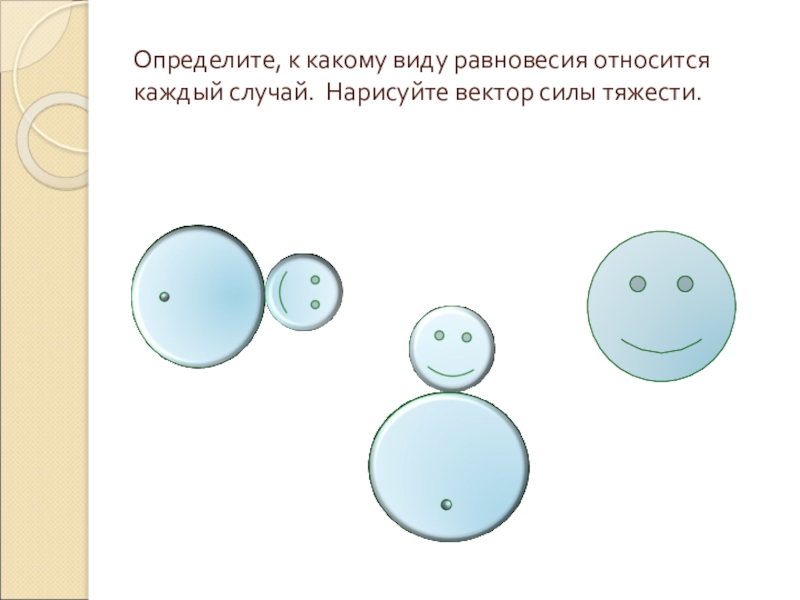
- 12. Определите, к какому виду равновесия относится каждый случай. Нарисуйте вектор силы тяжести.
- 13. Как можно увеличить устойчивость тела?Какое тело
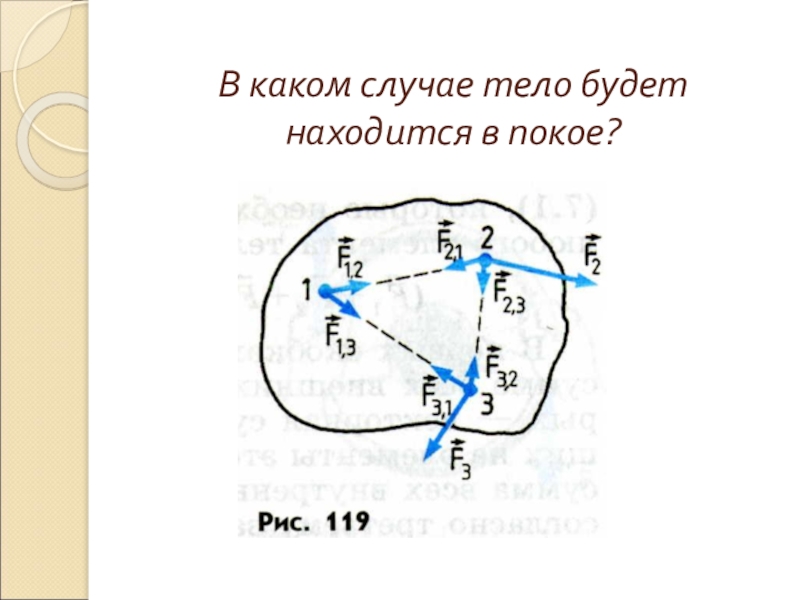
- 14. В каком случае тело будет находится в покое?
- 15. Условия равновесияЛЕБЕДЬ, ЩУКА И РАК Когда в
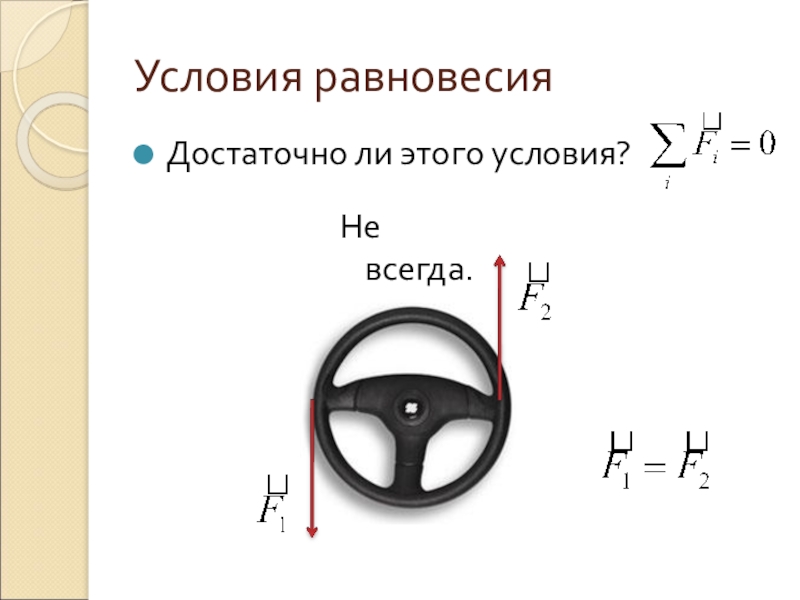
- 16. Условия равновесияДостаточно ли этого условия?Не всегда.
- 17. Необходимое и достаточное условие равновесия
- 18. Необходимое и достаточное условие равновесияДля равновесия тела
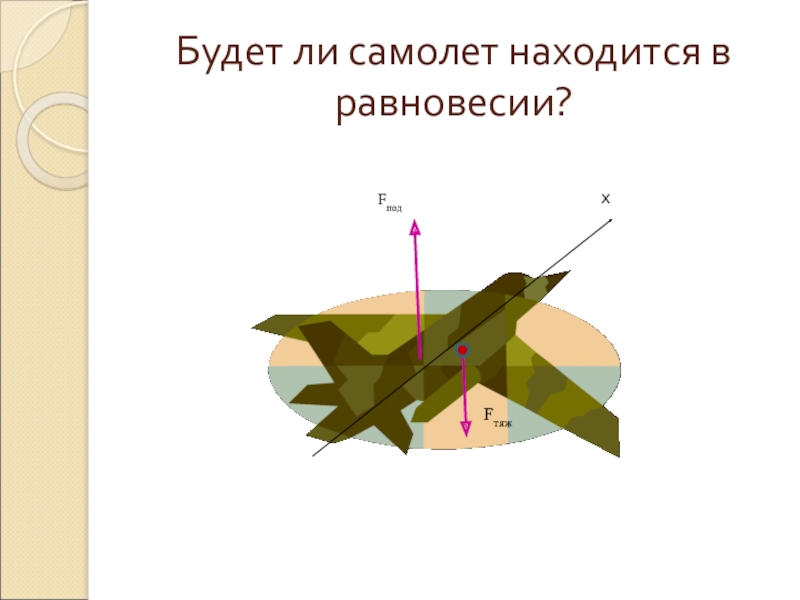
- 19. Будет ли самолет находится в равновесии?FтяжFподх
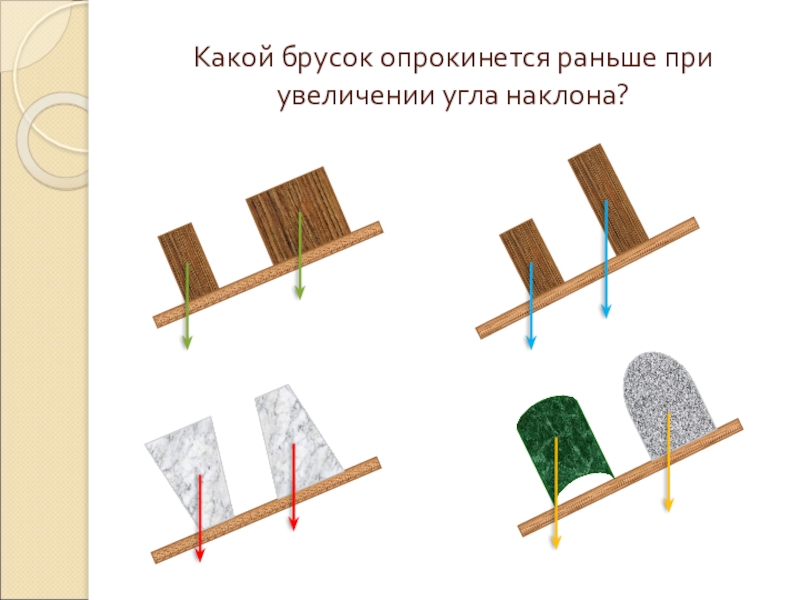
- 20. Какой брусок опрокинется раньше при увеличении угла наклона?
- 21. Алгоритм определения опрокидывания телаДа Нет Начало Определите
- 22. Какой брусок опрокинется раньше при увеличении угла наклона?
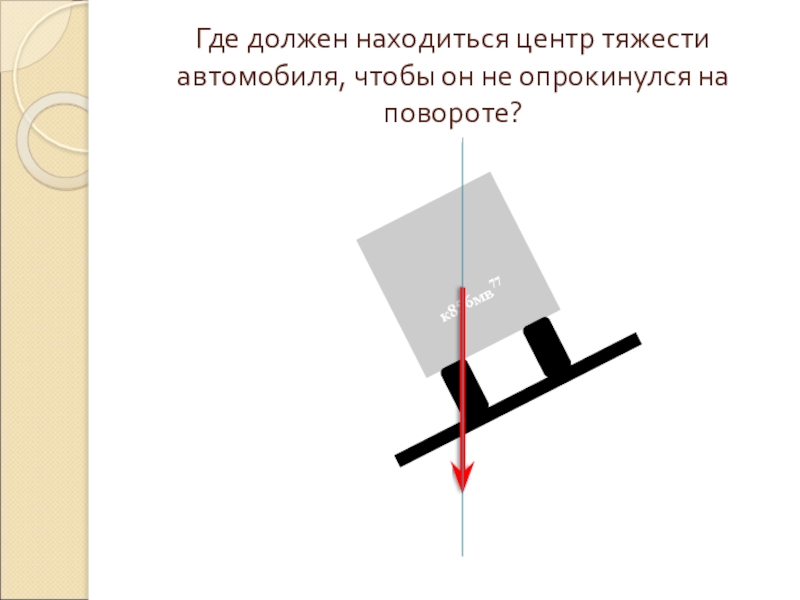
- 23. Где должен находиться центр тяжести автомобиля, чтобы он не опрокинулся на повороте?
- 24. Экспериментальная задача?
- 25. Экспериментальная задача?
- 26. Экспериментальная задачаЗадача на опрокидываниеFтяжТело опрокинется в том
- 27. Алгоритм решения задачи на скольжение тела
- 28. Алгоритм решения задачи на скольжение телаαхFтяжFтрNαFтяж yFтяж
- 29. Центр тяжестиЦентром тяжести тела называют геометрическую точку,
- 30. Методы определения центров тяжестиМетод симметрии. При определении
- 31. Центр тяжести тела произвольной формыКвадрат
- 32. Центр тяжести тела произвольной формыПрямоугольник
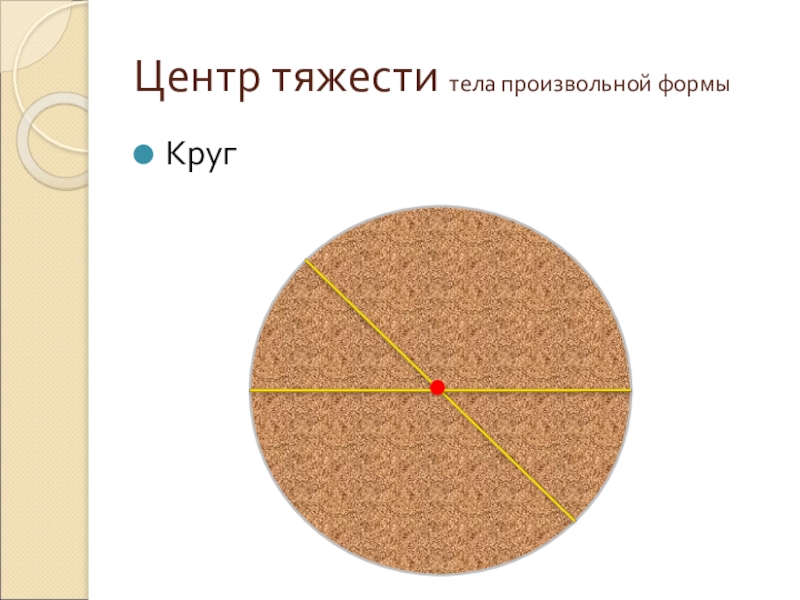
- 33. Центр тяжести тела произвольной формыКруг
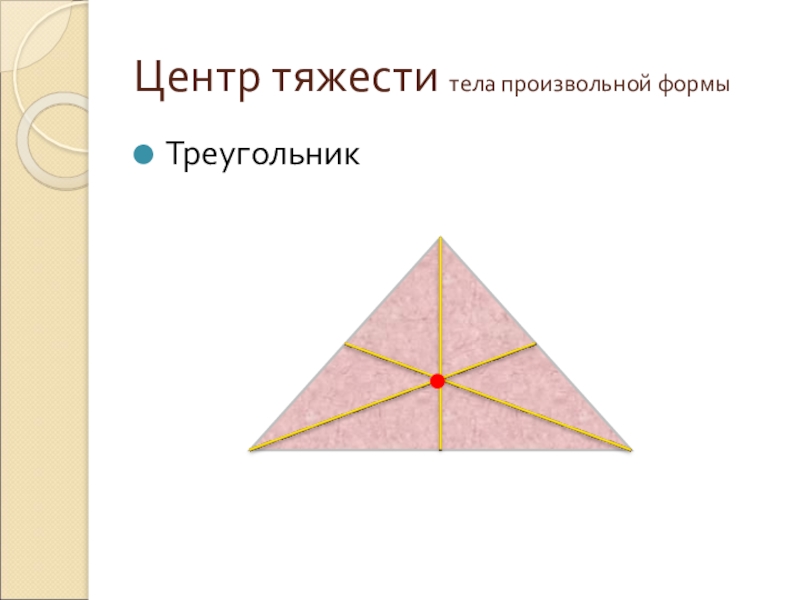
- 34. Центр тяжести тела произвольной формыТреугольник
- 35. Методы определения центров тяжестиМетод разбиения на части.
- 36. Центр тяжести тела произвольной формыЭкспериментальный метод
- 37. Центр тяжести тела произвольной формыЭкспериментальный метод
- 38. Центр тяжести тела произвольной формыРасчетный методxцт
- 39. Задача на определение центра масс двойной звездной
- 40. На самом деле это не одна звезда,
- 41. Задача на определение центра масс двойной звездной
- 42. Задача на определение центра масс двойной звездной
- 43. Методы определения центров тяжестиМетод отрицательных масс. Fтяж1Fтяж2xцт
- 44. Методы определения центров тяжестиМетод отрицательных масс. Fтяж1Fтяж2xцтОтвет:
- 45. Прочитайте текст и ответьте на вопросыЗачем центр
- 46. Домашнее заданиеучебник «Физика-10» Мякишев Г.Я., Буховцев Б.Б.,
- 47. Потому, что площадь опоры резко уменьшается. Ходить
- 48. Равновесие тела, имеющего площадь опорыдля равновесия необходимо,
- 49. Как лучше всего класть книги, если Вы
Виды равновесия
Слайд 12Определите, к какому виду равновесия относится каждый случай. Нарисуйте вектор силы
тяжести.
Слайд 13Как можно увеличить
устойчивость тела?
Какое тело более устойчиво: массивное или легкое?
Площадь
опоры меньше или больше?
У которого центр тяжести низко или высоко?
У которого центр тяжести низко или высоко?
Слайд 15Условия равновесия
ЛЕБЕДЬ, ЩУКА И РАК
Когда в товарищах согласья нет,
На
лад их дело не пойдет,
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак, да Щука
Везти с поклажей воз взялись,
И вместе трое все в него впряглись;
Из кожи лезут вон, а возу все нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвется в облака,
Рак пятится назад, а Щука тянет в воду.
Кто виноват из них, кто прав,- судить не нам;
Да только воз и ныне там.
И выйдет из него не дело, только мука.
Однажды Лебедь, Рак, да Щука
Везти с поклажей воз взялись,
И вместе трое все в него впряглись;
Из кожи лезут вон, а возу все нет ходу!
Поклажа бы для них казалась и легка:
Да Лебедь рвется в облака,
Рак пятится назад, а Щука тянет в воду.
Кто виноват из них, кто прав,- судить не нам;
Да только воз и ныне там.
Слайд 18Необходимое и достаточное условие равновесия
Для равновесия тела необходимо и достаточно, чтобы
моменты всех сил относительно оси вращения были уравновешены:
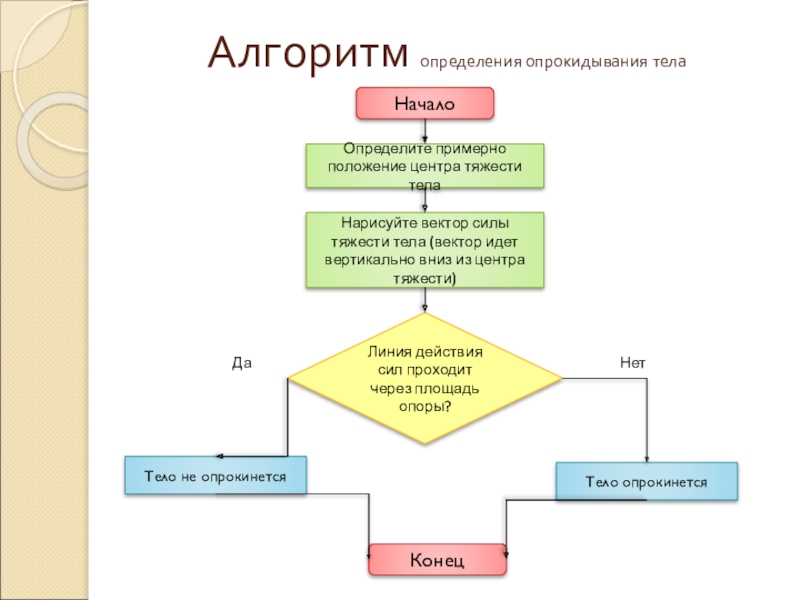
Слайд 21Алгоритм определения опрокидывания тела
Да
Нет
Начало
Определите примерно положение центра тяжести
тела
Нарисуйте вектор силы тяжести тела (вектор идет вертикально вниз из центра тяжести)
Линия действия сил проходит через площадь опоры?
Тело не опрокинется
Тело опрокинется
Конец
Слайд 26Экспериментальная задача
Задача на опрокидывание
Fтяж
Тело опрокинется в том случае, если вектор силы
тяжести не проходит через площадь опоры.
Найдем угол наклона плоскости α, при котором начнется опрокидывание тела: он должен быть равен углу β .
Угол β найдем из геометрических соображений (треугольник АВС):
Найдем угол наклона плоскости α, при котором начнется опрокидывание тела: он должен быть равен углу β .
Угол β найдем из геометрических соображений (треугольник АВС):
А
С
В
β
α
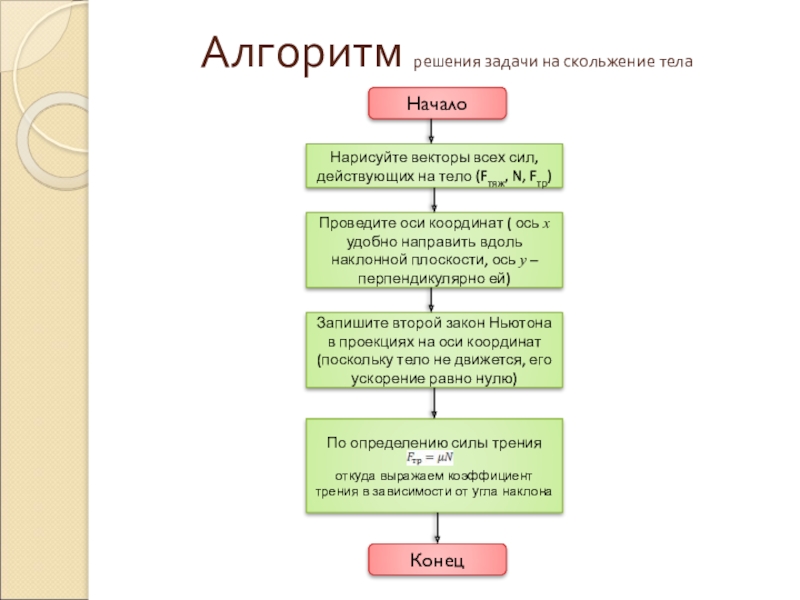
Слайд 28Алгоритм решения задачи на скольжение тела
α
х
Fтяж
Fтр
N
α
Fтяж y
Fтяж x
Fтяж x ≥ μ
Fтяж y
Fтяж sinα ≥ μ Fтяж cosα
Fтяж sinα ≥ μ Fтяж cosα
Fтяж x= Fтяж sinα
Fтяж y= Fтяж cosα
Fтр ≤ Fтяж x
Fтр = μ N
N= Fтяж y
tg α ≥ μ
Слайд 29Центр тяжести
Центром тяжести тела называют геометрическую точку, через которую проходит сила
тяжести тела при любом его положении в пространстве.
Понятие о центре тяжести было впервые изучено примерно 2200 лет назад греческим геометром Архимедом, величайшим математиком древности. С тех пор это понятие стало одним из важнейших в механике, а также позволило сравнительно просто решать некоторые геометрические задачи.
Слайд 30Методы определения центров тяжести
Метод симметрии. При определении центров тяжести широко используется
симметрия тел. Для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для однородного тела, имеющего ось или центр симметрии, центр тяжести находится соответственно на оси симметрии или в центре симметрии.
Слайд 35Методы определения центров тяжести
Метод разбиения на части. Некоторые тела сложной формы
можно разбить на части, центры тяжести которых известны. В таких случаях центры тяжести сложных фигур вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито.
Слайд 39Задача на определение центра масс двойной звездной системы
Самая яркая звезда северного
полушария неба – Сириус из созвездия Большого Пса
Слайд 40На самом деле это не одна звезда, а две, вращающиеся вокруг
общего центра масс: Сириус А – белая звезда главной последовательности (спектральный класс А1),– и Сириус B – белый карлик.
Задача на определение центра масс двойной звездной системы
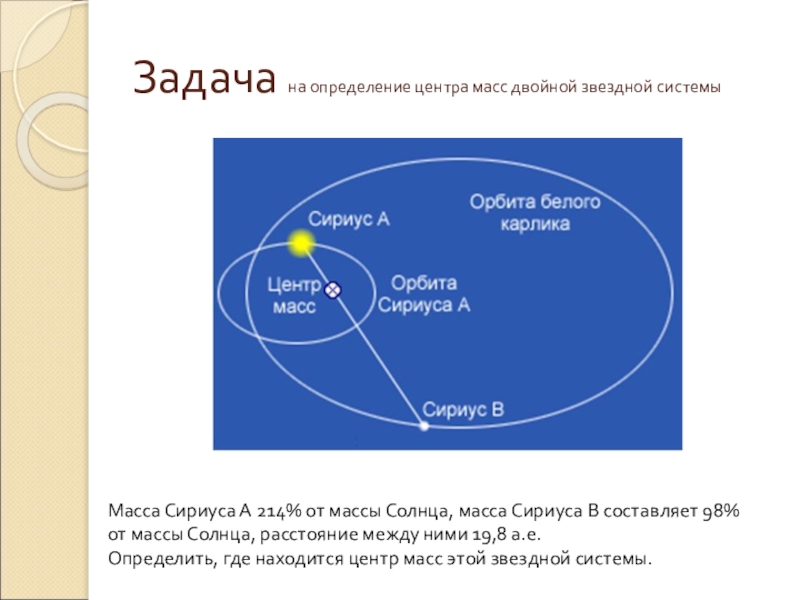
Слайд 41Задача на определение центра масс двойной звездной системы
Масса Сириуса А 214%
от массы Солнца, масса Сириуса B составляет 98% от массы Солнца, расстояние между ними 19,8 а.е.
Определить, где находится центр масс этой звездной системы.
Определить, где находится центр масс этой звездной системы.
Слайд 42Задача на определение центра масс двойной звездной системы
Ответ: центр масс двойной
звезды Сириус находится примерно на трети расстояния между ними ближе к Сириусу А.
Слайд 44Методы определения центров тяжести
Метод отрицательных масс.
Fтяж1
Fтяж2
xцт
Ответ: центр тяжести фигуры находится
на расстоянии R/6 от центра большого круга.
Слайд 45Прочитайте текст и ответьте на вопросы
Зачем центр тяжести располагают как можно
ниже?
Что заставляет плавающее тело поворачиваться, если центр тяжести не находится над точкой опоры?
Какая сила опрокидывает корабль в шторм, если грузы сместились?
Где должна располагаться точка приложения подъемной силы самолета, чтобы он был устойчивым?
Какая энергия минимальна у устойчивого тела?
Что заставляет плавающее тело поворачиваться, если центр тяжести не находится над точкой опоры?
Какая сила опрокидывает корабль в шторм, если грузы сместились?
Где должна располагаться точка приложения подъемной силы самолета, чтобы он был устойчивым?
Какая энергия минимальна у устойчивого тела?
Слайд 46Домашнее задание
учебник «Физика-10» Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н., §54-56, упр.10
№3, 5, 7.
1. Придумать и решить задачу на нахождение центра тяжести сложной фигуры;
2. Найти центр тяжести системы тел;
3. Придумать эксперимент по определению центра тяжести объемного тела произвольной формы (картофелины);
4. Сделать воздушного змея и привязать к нему бечевку так, чтобы он хорошо слушался управления.
1. Придумать и решить задачу на нахождение центра тяжести сложной фигуры;
2. Найти центр тяжести системы тел;
3. Придумать эксперимент по определению центра тяжести объемного тела произвольной формы (картофелины);
4. Сделать воздушного змея и привязать к нему бечевку так, чтобы он хорошо слушался управления.
Слайд 47 Потому, что площадь опоры резко уменьшается. Ходить по канату нелегко, и
не даром награждают аплодисментами искусного канатоходца. Однако иногда зрители впадают в ошибку и признают за вершину мастерства хитрые трюки, облегчающие задачу. Артист берёт сильно изогнутое коромысло с двумя вёдрами воды; вёдра оказываются на уровне каната. С серьёзным лицом, при замолкшем оркестре, артист совершает переход по канату. Как усложнён трюк, думает неопытный зритель. На самом же деле артист облегчил свою задачу, понизив центр тяжести.
Почему нелегко ходить по канату?
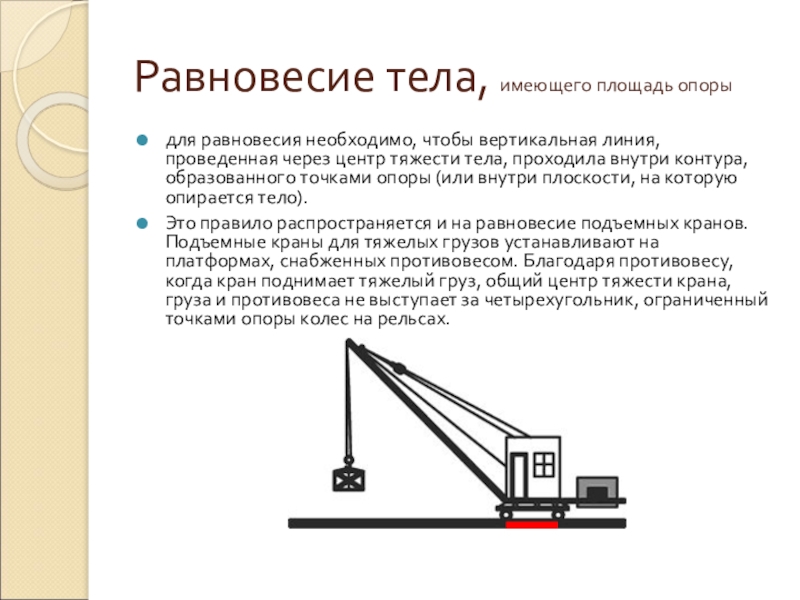
Слайд 48Равновесие тела, имеющего площадь опоры
для равновесия необходимо, чтобы вертикальная линия, проведенная
через центр тяжести тела, проходила внутри контура, образованного точками опоры (или внутри плоскости, на которую опирается тело).
Это правило распространяется и на равновесие подъемных кранов. Подъемные краны для тяжелых грузов устанавливают на платформах, снабженных противовесом. Благодаря противовесу, когда кран поднимает тяжелый груз, общий центр тяжести крана, груза и противовеса не выступает за четырехугольник, ограниченный точками опоры колес на рельсах.
Это правило распространяется и на равновесие подъемных кранов. Подъемные краны для тяжелых грузов устанавливают на платформах, снабженных противовесом. Благодаря противовесу, когда кран поднимает тяжелый груз, общий центр тяжести крана, груза и противовеса не выступает за четырехугольник, ограниченный точками опоры колес на рельсах.
Слайд 49Как лучше всего класть книги, если Вы хотите составить из них
стопку, причем так, чтобы наклон был как можно больше?
