- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике ЭМВ
Содержание
- 1. Презентация по физике ЭМВ
- 2. МатематикеФизике
- 3. Вспомним1Правила
- 4. геометрический смысл;для отыскания наибольшего и наименьшего значений;для исследования функций
- 5. Геометрический смысл производной: Если
- 6. Задание B8 (№ 6037,банк заданий fipi)Прямая
- 7. Геометрический смысл производной:На рисунке изображён график функции
- 8. Геометрический смысл производной:На рисунке изображён график функции
- 9. Задание B8 (№ 9605,банк заданий
- 10. Алгоритм нахождения наибольшего и наименьшего на [а;b]
- 11. Задание B11Найдите наименьшее значение функции y=3x2-6x-9 на отрезке (1/7; 8/7)
- 12. Задание B11 (№ 3413,банк заданий fipi) Найдите наибольшее значение функции y=11x-9sinx+3на отрезке [-π/2;0].
- 13. Исследование функции при помощи производной:Если f(x) возрастает
- 14. Исследование функций:Задание B8 (№ 6871,банк заданий
- 15. Задание B8 (№ 6869,банк заданий fipi)На
- 16. Задание B8 (№ 6429,банк заданий fipi)На рисунке
- 17. Исследование функций:Функция f(x) определена на [-8;8]. На
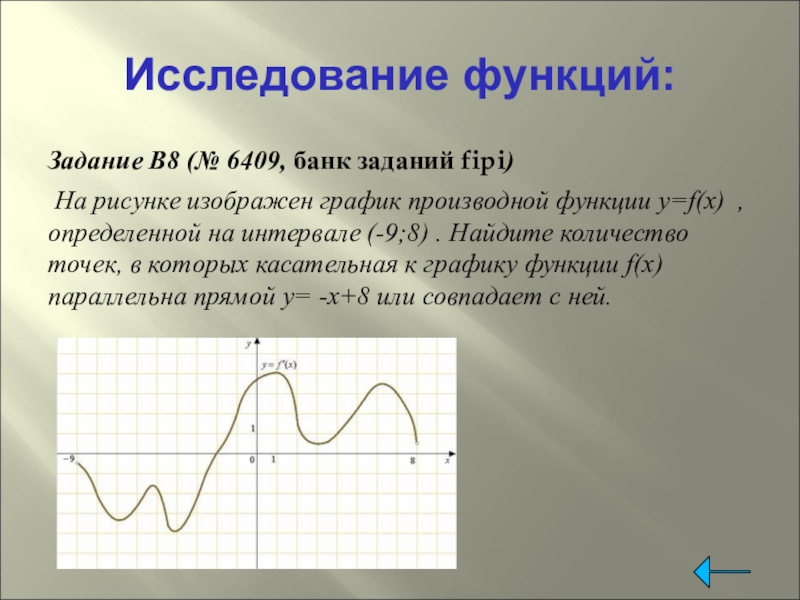
- 18. Исследование функций:Задание B8 (№ 6409, банк заданий
- 19. Применение производной в физике
- 20. Механика
- 21. Колебательный контур состоит из конденсатора емкостью 1мкФ
- 22. Слайд 22
- 23. На рисунке приведен график гармонического колебания маятника
- 24. Решение:xmax= 0,5см = 0,005мT = 4cω0 =
- 25. Домашнее задание:1.Повторить решение систем уравнений с двумя переменными.2. Решить тест.
МатематикеФизике
Слайд 3Вспомним
1Правила
2Табличное дифференцирование
(f±g)׳=f ׳± g ׳ (C)׳= (tgx)׳=
(f g)׳=f ׳g+f g ׳ (x)׳= (ctgx)׳=
(f/g)׳=(f ׳g - f g ׳)/g² (xⁿ)׳= (1/x)׳=
(C f)׳=C f ׳ (cosx)׳= (√x)׳=
(f(kx+m))׳=kf ׳(kx+m) (sinx)׳=
(f±g)׳=f ׳± g ׳ (C)׳= (tgx)׳=
(f g)׳=f ׳g+f g ׳ (x)׳= (ctgx)׳=
(f/g)׳=(f ׳g - f g ׳)/g² (xⁿ)׳= (1/x)׳=
(C f)׳=C f ׳ (cosx)׳= (√x)׳=
(f(kx+m))׳=kf ׳(kx+m) (sinx)׳=
Слайд 4
геометрический смысл;
для отыскания наибольшего и наименьшего значений;
для исследования функций
Слайд 5Геометрический смысл производной:
Если к графику функции можно
провести касательную, не параллельную оси оу, в точке х=а, то f ׳(a) = tgα = k
Слайд 6
Задание B8 (№ 6037,банк заданий fipi)
Прямая y=6x+6 параллельна касательной к
графику функции y=x2+7x-7. Найдите абсциссу точки касания.
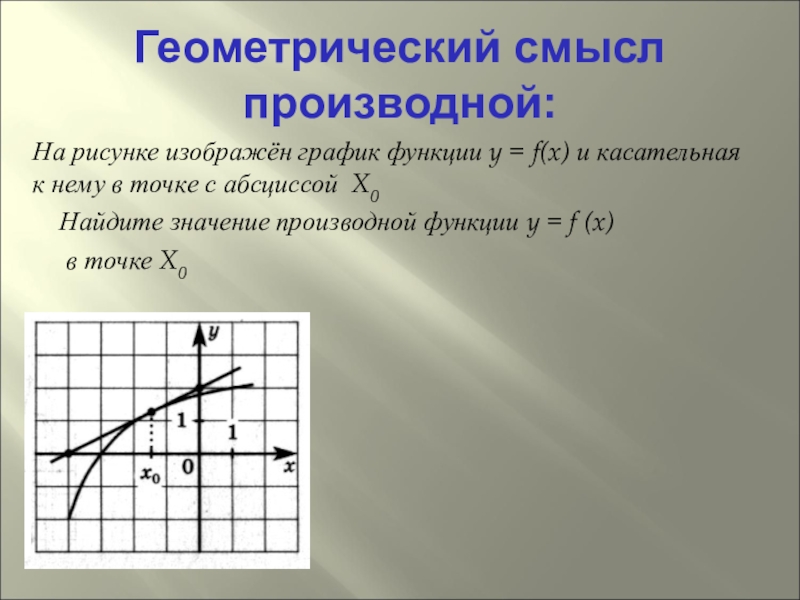
Слайд 7Геометрический смысл производной:
На рисунке изображён график функции y = f(x) и
касательная к нему в точке с абсциссой X0
Найдите значение производной функции y = f (x)
в точке X0
Найдите значение производной функции y = f (x)
в точке X0
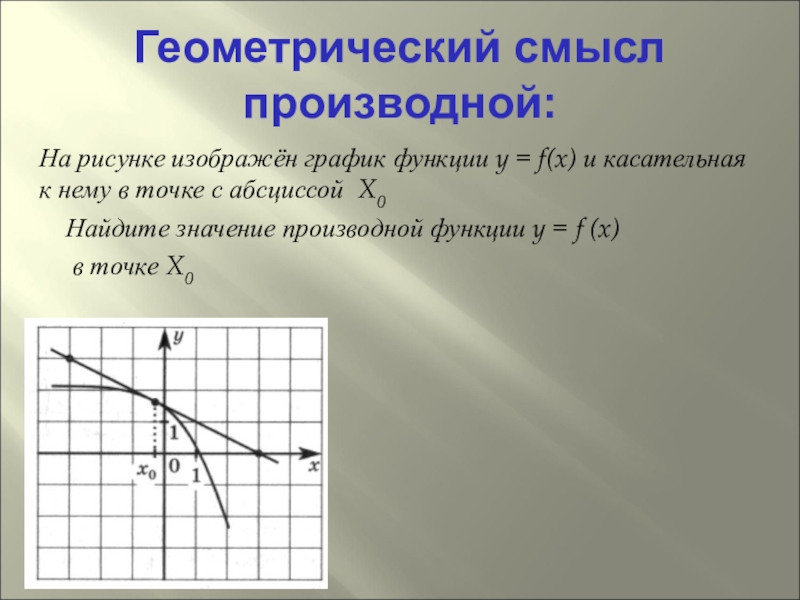
Слайд 8Геометрический смысл производной:
На рисунке изображён график функции y = f(x) и
касательная к нему в точке с абсциссой X0
Найдите значение производной функции y = f (x)
в точке X0
Найдите значение производной функции y = f (x)
в точке X0
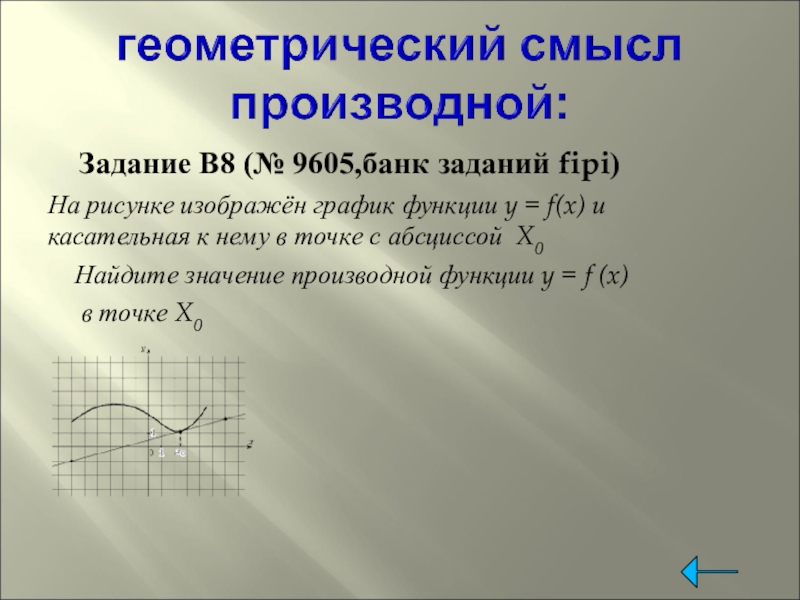
Слайд 9 Задание B8 (№ 9605,банк заданий fipi)
На рисунке изображён график
функции y = f(x) и касательная к нему в точке с абсциссой X0
Найдите значение производной функции y = f (x)
в точке X0
Найдите значение производной функции y = f (x)
в точке X0
Слайд 10Алгоритм нахождения наибольшего и наименьшего на [а;b] значений функции, непрерывной на
[a;b]:
1.Найти f׳(x);
2.Решив уравнение f׳(x)=0, выбрать критические точки, которые лежат внутри промежутка (a;b);
3.Найти значение функции в этих точках и на концах отрезка;
4.Из найденных значений выбрать наибольшее или наименьшее значение.
1.Найти f׳(x);
2.Решив уравнение f׳(x)=0, выбрать критические точки, которые лежат внутри промежутка (a;b);
3.Найти значение функции в этих точках и на концах отрезка;
4.Из найденных значений выбрать наибольшее или наименьшее значение.
Слайд 12Задание B11 (№ 3413,банк заданий fipi)
Найдите наибольшее значение функции y=11x-9sinx+3
на отрезке
[-π/2;0].
Слайд 13Исследование функции при помощи производной:
Если f(x) возрастает и дифференцируема на [a;b],
то f ׳(x) ≥ 0.
Если f(x) убывает и дифференцируема на [a;b],
то f ׳(x) ≤ 0.
Если f ׳(a) = 0 , то a – критическая точка.
Если f(x) убывает и дифференцируема на [a;b],
то f ׳(x) ≤ 0.
Если f ׳(a) = 0 , то a – критическая точка.
Слайд 14
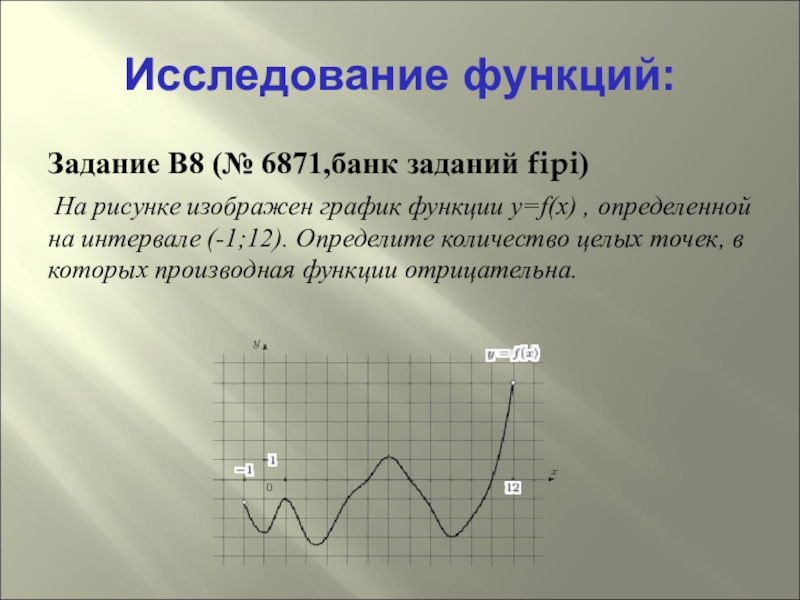
Исследование функций:
Задание B8 (№ 6871,банк заданий fipi)
На рисунке изображен график
функции y=f(x) , определенной на интервале (-1;12). Определите количество целых точек, в которых производная функции отрицательна.
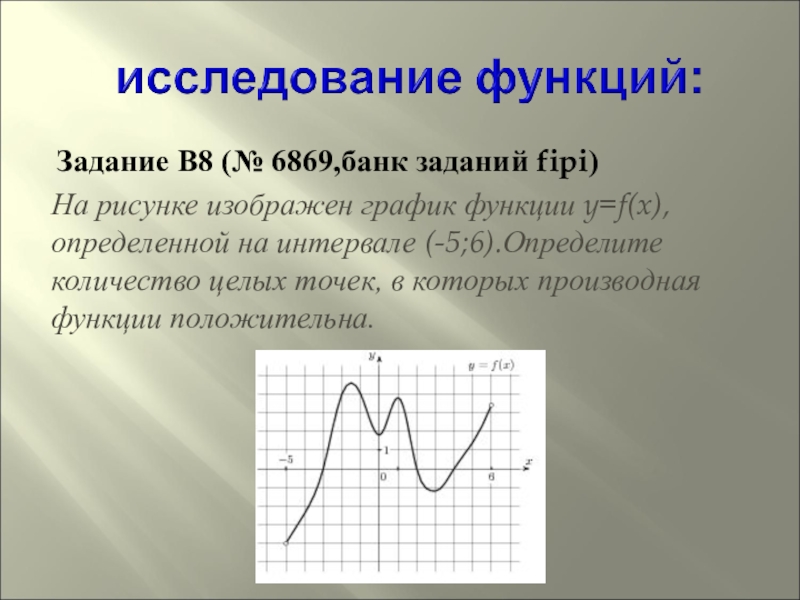
Слайд 15 Задание B8 (№ 6869,банк заданий fipi)
На рисунке изображен график функции
y=f(x), определенной на интервале (-5;6).Определите количество целых точек, в которых производная функции положительна.
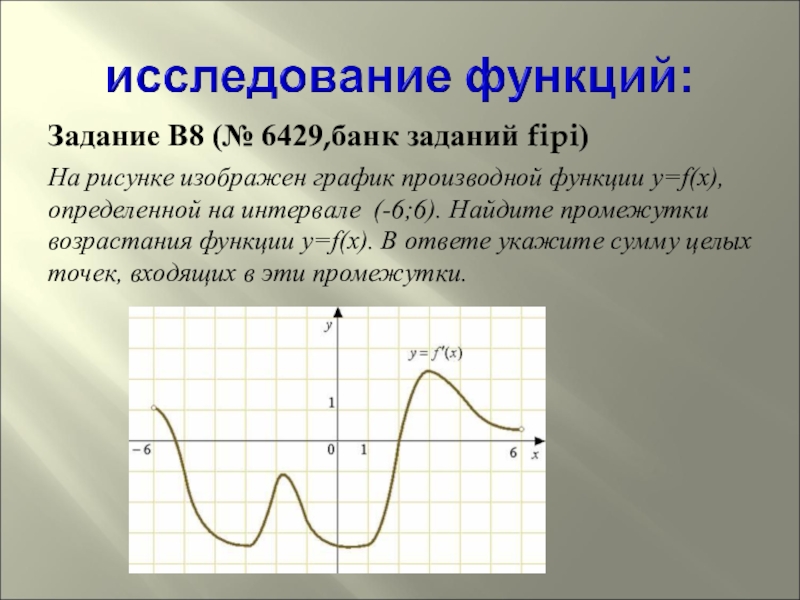
Слайд 16Задание B8 (№ 6429,банк заданий fipi)
На рисунке изображен график производной функции y=f(x),
определенной на интервале (-6;6). Найдите промежутки возрастания функции y=f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Слайд 17Исследование функций:
Функция f(x) определена на [-8;8]. На рисунке изображён график её
производной y=f׳(x). Найдите сумму точек экстремума этой функции.
Слайд 18Исследование функций:
Задание B8 (№ 6409, банк заданий fipi)
На рисунке изображен график производной
функции y=f(x) , определенной на интервале (-9;8) . Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y= -x+8 или совпадает с ней.
Слайд 20
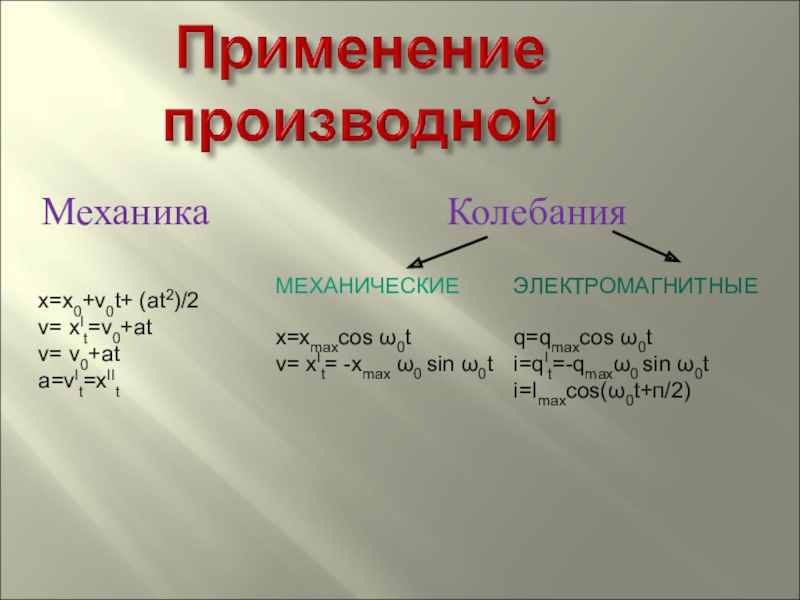
Механика
Колебания
x=x0+v0t+ (at2)/2
v= xIt=v0+at
v= v0+at
a=vIt=xIIt
МЕХАНИЧЕСКИЕ
x=xmaxcos ω0t
v= xIt= -xmax ω0 sin ω0t
ЭЛЕКТРОМАГНИТНЫЕ
q=qmaxcos ω0t
i=qIt=-qmaxω0 sin ω0t
i=Imaxcos(ω0t+п/2)
Слайд 21
Колебательный контур состоит из конденсатора емкостью 1мкФ и катушки индуктивностью 4гн.
Амплитуда колебаний заряда на конденсаторе 100 мкКл. Написать уравнение q=q(t). i=i(t), u=u(t). Найти амплитуду колебаний силы тока и напряжения.
Задача
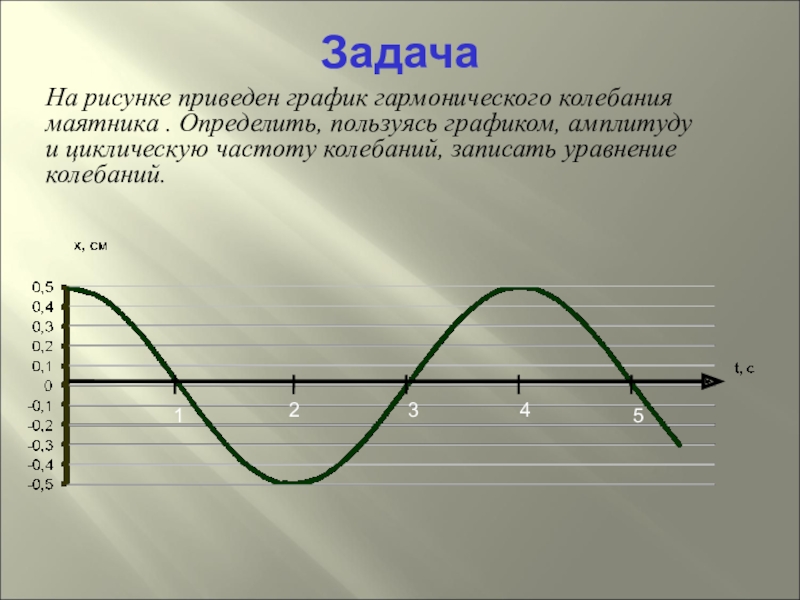
Слайд 23На рисунке приведен график гармонического колебания маятника . Определить, пользуясь графиком,
амплитуду и циклическую частоту колебаний, записать уравнение колебаний.
Задача
1
2
3
4
5
Слайд 24Решение:
xmax= 0,5см = 0,005м
T = 4c
ω0 = 2π/T = 2π/4 =
π/2(рад/с)
x = x0 cos ω0 t
x = 0,005 cos π/2 t
x = x0 cos ω0 t
x = 0,005 cos π/2 t






![Презентация по физике ЭМВ Алгоритм нахождения наибольшего и наименьшего на [а;b] значений функции, непрерывной на Алгоритм нахождения наибольшего и наименьшего на [а;b] значений функции, непрерывной на [a;b]:1.Найти f׳(x);2.Решив уравнение f׳(x)=0, выбрать критические](/img/thumbs/b354c37640001249fd90d0727876b721-800x.jpg)

![Презентация по физике ЭМВ Задание B11 (№ 3413,банк заданий fipi) Найдите наибольшее значение функции y=11x-9sinx+3на отрезке [-π/2;0]. Задание B11 (№ 3413,банк заданий fipi) Найдите наибольшее значение функции y=11x-9sinx+3на отрезке [-π/2;0].](/img/thumbs/5fcf2a57108c2f5674d330da42d18354-800x.jpg)
![Презентация по физике ЭМВ Исследование функции при помощи производной:Если f(x) возрастает и дифференцируема на [a;b], Исследование функции при помощи производной:Если f(x) возрастает и дифференцируема на [a;b], то f ׳(x) ≥ 0. Если](/img/thumbs/a773269e7847aea0e09768e683986858-800x.jpg)
![Презентация по физике ЭМВ Исследование функций:Функция f(x) определена на [-8;8]. На рисунке изображён график её Исследование функций:Функция f(x) определена на [-8;8]. На рисунке изображён график её производной y=f׳(x). Найдите сумму точек экстремума](/img/thumbs/1e3cde67eab3565ae2cccddd444559b5-800x.jpg)