- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по физике Архимед
Содержание
- 1. Презентация по физике Архимед
- 2. Введение Физика - наука
- 3. Архиме́д - древнегреческий математик
- 4. Слайд 4
- 5. Биография Сведения о жизни
- 6. Александрия В Александрии Архимед познакомился и подружился со знаменитыми
- 7. ЛегендыАрхимед переворачивает планету Земля.
- 8. Уже при жизни
- 9. Осада Сиракуз Инженерный гений
- 10. Смерть АрхимедаЭдуар Вимон (1846—1930). Смерть Архимеда
- 11. Рассказ о смерти Архимеда от рук римлян
- 12. Предполагаемая гробница Архимеда в Сиракузах
- 13. Плутарх утверждает, что
- 14. Научная деятельность По словам Плутарха,
- 15. Задача о трисекции угла
- 16. Задача о делении угла на три равные
- 17. Измерение круга Задача о
- 18. Архимед физик Архимеда справедливо
- 19. Оптика В своем стремлении
- 20. Архимедов винт
- 21. Архимедов винт, винт Архимеда — механизм, исторически использовавшийся для передачи
- 22. Принцип работы Машина состоит
- 23. Современные Архимедовы винты, используемые для осушения польдеров в Голландии
- 24. Применение Издавна архимедов винт
- 25. Спираль АрхимедаАрхимедова спираль — спираль, плоская кривая, траектория точки M , которая
- 26. Слайд 26
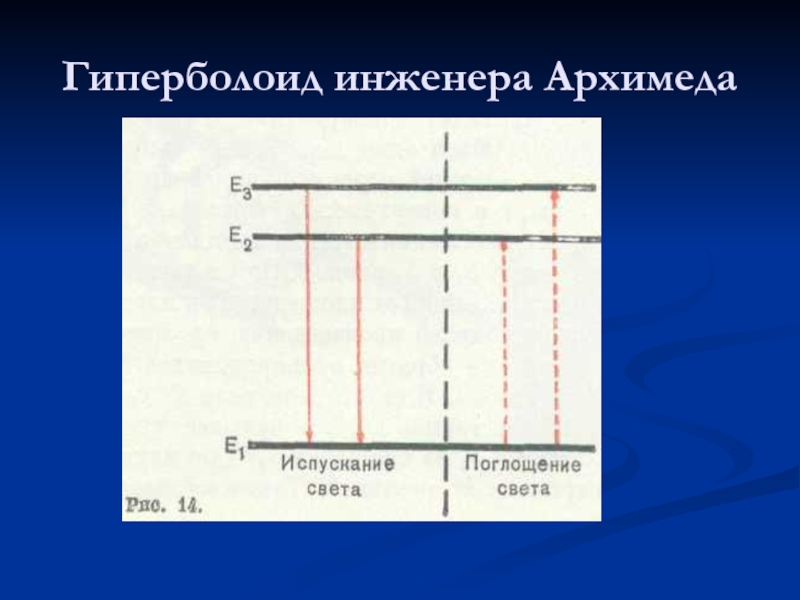
- 27. Гиперболоид инженера Архимеда
- 28. Действительно ли хитроумный
- 29. Подготовка зеркал, «выстрел», дым, огонь, дыра между досками.
- 30. Паровая пушка
- 31. Итальянская группа учёных
- 32. Закон АрхимедаЗакон Архимеда: на всякое тело, погруженное
- 33. Слайд 33
- 34. Условие плавания телПоведение тела, находящегося в жидкости
- 35. История развития подводных лодок
- 36. Слайд 36
- 37. В 1834 г.
- 38. Слайд 38
- 39. Лишь в 1884
- 40. Влияние работ Архимеда на развитие физики
- 41. В эпоху Возрождения,
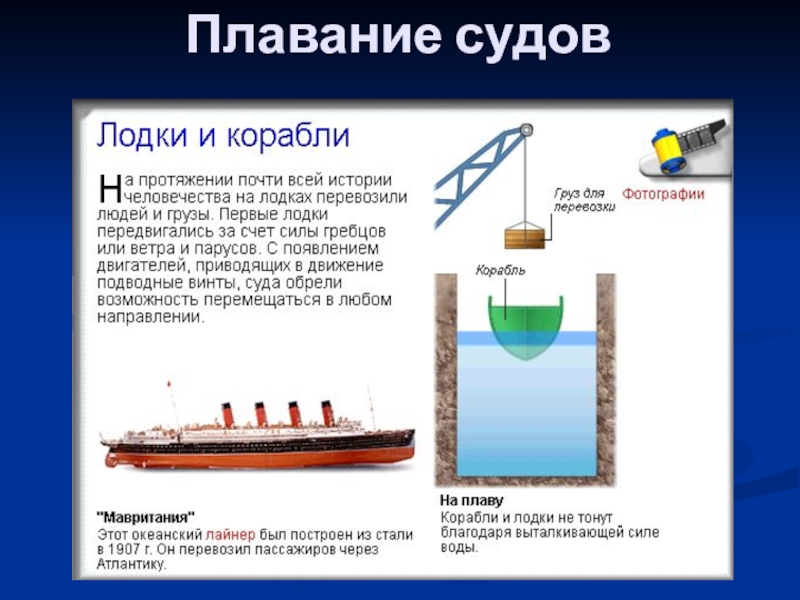
- 42. Плавание судов
- 43. Плавание тел
- 44. Плавание судов
- 45. Корабль, 2700-е годы до н.э.
- 46. “Санта-Мария”1492 г.
- 47. Корабль “Уэрриор” 1860 г. (с паровым двигателем)
- 48. Судно “Шин Айтоку Мару” 1980 г. (с компьютерным управлением)
- 49. Суда на воздушной подушке
- 50. Подводные лодки
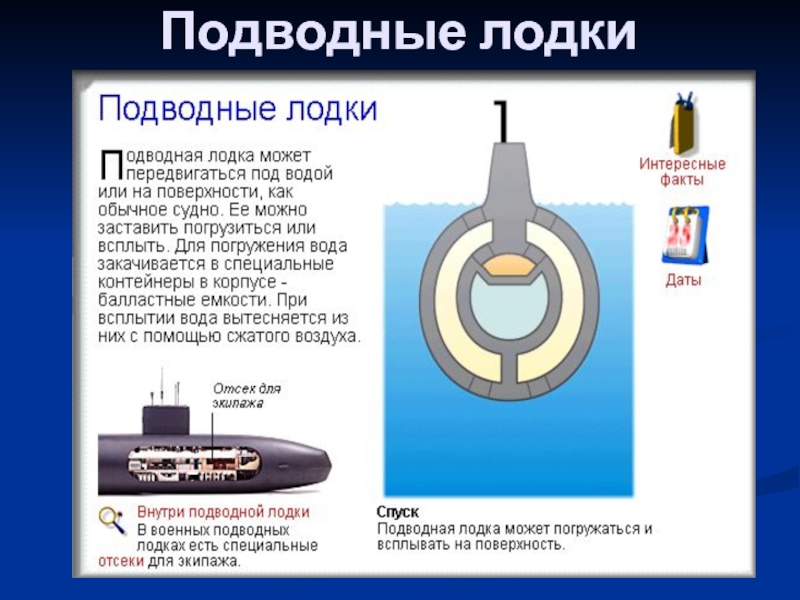
- 51. Подводные лодки
- 52. Первая подводная лодка Шильдера
- 53. Современные подводные лодкиАтомная ракетная подводная лодка
- 54. Современные подводные лодки
- 55. Заключение Если окинуть взглядом разнообразную и плодотворную
- 56. В астрономии Архимед предстает перед нами
- 57. Спасибо за просмотр
Введение Физика - наука о природе, изучающая простейшие и вместе с тем наиболее общие закономерности природы, строение и законы движения материи. Физику относят к точным наукам. Ее понятия и законы
Слайд 2Введение
Физика - наука о природе, изучающая простейшие
и вместе с тем наиболее общие закономерности природы, строение и законы движения материи. Физику относят к точным наукам. Ее понятия и законы составляют основу естествознания. Границы, разделяющие физику и другие естественные науки, исторически условны. Принято считать, что в своей основе физика является наукой экспериментальной, поскольку открытые ею законы основаны на установленных опытным путем данных. Физические законы представляются в виде количественных соотношений, выраженных на языке математики. В целом физика разделяется на экспериментальную, имеющую дело с проведением экспериментов с целью установления новых фактов и проверки гипотез и известных физических законов, и теоретическую, ориентированную на формулировку физических законов, объяснение на основе этих законов природных явлений и предсказание новых явлений.
Несомненно, Архимед — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.
Несомненно, Архимед — самый гениальный учёный Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими математиками всех времён. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.
Слайд 3
Архиме́д - древнегреческий математик физик, механик и инженер из Сиракуз.
Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений. Архимед родился в 287 году до нашей эры в греческом городе Сиракузы, где и прожил почти всю свою жизнь. Отцом его был Фидий, придворный астроном правителя города Гиерона. Учился Архимед, как и многие другие древнегреческие ученые, в Александрии, где правители Египта Птолемеи собрали лучших греческих ученых и мыслителей, а также основали знаменитую, самую большую в мире библиотеку.
Слайд 5Биография
Сведения о жизни Архимеда оставили нам Полибий ,Тит
Ливий, Цицерон, Плутарх, Витрувий и другие. Они жили на много лет позже описываемых событий, и достоверность этих сведений оценить трудно.
Архимед родился в Сиракузах, греческой колонии на острове Сицилия. Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механики и астрономии. Для обучения Архимед отправился в Александрию Египетскую — научный и культурный центр того времени.
Архимед родился в Сиракузах, греческой колонии на острове Сицилия. Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механики и астрономии. Для обучения Архимед отправился в Александрию Египетскую — научный и культурный центр того времени.
Слайд 6Александрия
В Александрии Архимед познакомился и подружился со знаменитыми учёными: астрономом Кононом, разносторонним учёным Эратосфеном,
с которыми потом переписывался до конца жизни. В то время Александрия славилась своей библиотекой, в которой было собрано более 700 тыс. рукописей.
По-видимому, именно здесь Архимед познакомился с трудами Демокрита, Евдокса и других замечательных греческих геометров, о которых он упоминал и в своих сочинениях.
По окончании обучения Архимед вернулся в Сицилию. В Сиракузах он был окружён вниманием и не нуждался в средствах. Из-за давности лет жизнь Архимеда тесно переплелась с легендами о нём.
По-видимому, именно здесь Архимед познакомился с трудами Демокрита, Евдокса и других замечательных греческих геометров, о которых он упоминал и в своих сочинениях.
По окончании обучения Архимед вернулся в Сицилию. В Сиракузах он был окружён вниманием и не нуждался в средствах. Из-за давности лет жизнь Архимеда тесно переплелась с легендами о нём.
Слайд 8
Уже при жизни Архимеда вокруг его имени
создавались легенды поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том, как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота или ювелир подмешал туда значительное количество серебра. Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объём короны: ведь она имела неправильную форму! Архимед всё время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить её объём, измерив объём вытесненной ею воды. Согласно легенде, Архимед выскочил голый на улицу с криком «Эврика!» ,то есть «Нашёл!». В этот момент был открыт основной закон гидростатики: закон Архимеда.
Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею тяжёлый многопалубный корабль «Сиракузия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. По легенде, Архимед заявил при этом: «Будь в моём распоряжении другая Земля, на которую можно было бы встать, я сдвинул бы с места нашу» (в другом варианте: «Дайте мне точку опоры, и я сдвину Землю»).
Существует легенда, что Архимед создал лучевое оружие. Можно поверить греческому писателю Плутарху, который пишет, что, когда корабли римского полководца Марка Марцелла приблизились с моря к Сиракузам на расстояние полета стрелы, тысячи зеркал отразили яркие лучи солнца на корабли Марцелла. На римских кораблях начался страшный пожар, и они были обращены в пепел. Это подтверждается и словами Аупиана из Самосаты, который в одной из своих речей, говоря о науке, обращается к великому Архимеду, “который при помощи своего искусства сжег неприятельские корабли”.
Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею тяжёлый многопалубный корабль «Сиракузия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. По легенде, Архимед заявил при этом: «Будь в моём распоряжении другая Земля, на которую можно было бы встать, я сдвинул бы с места нашу» (в другом варианте: «Дайте мне точку опоры, и я сдвину Землю»).
Существует легенда, что Архимед создал лучевое оружие. Можно поверить греческому писателю Плутарху, который пишет, что, когда корабли римского полководца Марка Марцелла приблизились с моря к Сиракузам на расстояние полета стрелы, тысячи зеркал отразили яркие лучи солнца на корабли Марцелла. На римских кораблях начался страшный пожар, и они были обращены в пепел. Это подтверждается и словами Аупиана из Самосаты, который в одной из своих речей, говоря о науке, обращается к великому Архимеду, “который при помощи своего искусства сжег неприятельские корабли”.
Слайд 9Осада Сиракуз
Инженерный гений Архимеда с особой силой
проявился во время осады Сиракуз римлянами в 212 году до н. э. в ходе Второй Пунической войны. А ведь в это время ему было уже 75 лет! Построенные Архимедом мощные метательные машины забрасывали римские войска тяжёлыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время лёгкие метательные машины близкого действия забросали их градом ядер. Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули.
Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца». Но даже во время осады Архимед не давал покоя римлянам. По легенде, во время осады римский флот был сожжён защитниками города, которые при помощи зеркал и отполированных до блеска щитов сфокусировали на них солнечные лучи по приказу Архимеда.
Легенда была дважды опровергнута в телепередаче «Разрушители легенд» (в 46-м и 16-м выпусках). Существует мнение, что корабли поджигались метко брошенными зажигательными снарядами, а сфокусированные лучи служили лишь прицельной меткой для баллист.
Однако эксперимент греческого учёного Иоанниса Саккаса (1973) показал иное. Он использовал 70 медных зеркал и с их помощью успешно поджёг фанерную модель римского корабля с расстояния 50 м.
Только вследствие измены Сиракузы были взяты римлянами осенью 212 году до н. э. При этом Архимед был убит.
Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело… римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца». Но даже во время осады Архимед не давал покоя римлянам. По легенде, во время осады римский флот был сожжён защитниками города, которые при помощи зеркал и отполированных до блеска щитов сфокусировали на них солнечные лучи по приказу Архимеда.
Легенда была дважды опровергнута в телепередаче «Разрушители легенд» (в 46-м и 16-м выпусках). Существует мнение, что корабли поджигались метко брошенными зажигательными снарядами, а сфокусированные лучи служили лишь прицельной меткой для баллист.
Однако эксперимент греческого учёного Иоанниса Саккаса (1973) показал иное. Он использовал 70 медных зеркал и с их помощью успешно поджёг фанерную модель римского корабля с расстояния 50 м.
Только вследствие измены Сиракузы были взяты римлянами осенью 212 году до н. э. При этом Архимед был убит.
Слайд 11Рассказ о смерти Архимеда от рук римлян существует в нескольких версиях:
1.
Рассказ Иоанна Цеца (Chiliad, книга II): в разгар боя 75-летний Архимед сидел на пороге своего дома, углублённо размышляя над чертежами, сделанными им прямо на дорожном песке. В это время пробегавший мимо римский воин наступил на чертёж, и возмущённый учёный бросился на римлянина с криком: «Не тронь моих чертежей!» Солдат остановился и хладнокровно зарубил старика мечом.
2. Рассказ Плутарха: «К Архимеду подошёл солдат и объявил, что его зовёт Марцелл. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешённой. Солдат, которому не было дела до его доказательства, рассердился и пронзил его своим мечом».
3. Воин ворвался в дом Архимеда для грабежа, занёс меч на хозяина, а тот только и успел крикнуть: «Остановись, подожди хотя бы немного. Я хочу закончить решение задачи, а потом делай что хочешь!»
4. Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что учёный несёт в ларце золото или драгоценности, и, недолго думая, перерезали ему горло.
2. Рассказ Плутарха: «К Архимеду подошёл солдат и объявил, что его зовёт Марцелл. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешённой. Солдат, которому не было дела до его доказательства, рассердился и пронзил его своим мечом».
3. Воин ворвался в дом Архимеда для грабежа, занёс меч на хозяина, а тот только и успел крикнуть: «Остановись, подожди хотя бы немного. Я хочу закончить решение задачи, а потом делай что хочешь!»
4. Архимед сам отправился к Марцеллу, чтобы отнести ему свои приборы для измерения величины Солнца. По дороге его ноша привлекла внимание римских солдат. Они решили, что учёный несёт в ларце золото или драгоценности, и, недолго думая, перерезали ему горло.
Слайд 13
Плутарх утверждает, что генерал Марцелл был разгневан
гибелью Архимеда, которого он якобы приказал не трогать.
Таковы легенды. Однако многие историки полагают, что Архимед был убит не случайно — ведь его ум стоил в те времена целой армии.
Цицерон, бывший квестором на Сицилии в 75 году до н. э., пишет в «Тускуланских беседах» (книга V), что ему в 75 году до н. э., спустя 137 лет после этих событий, удалось обнаружить полуразрушенную могилу Архимеда; на ней, как и завещал Архимед, было изображение шара, вписанного в цилиндр.
Таковы легенды. Однако многие историки полагают, что Архимед был убит не случайно — ведь его ум стоил в те времена целой армии.
Цицерон, бывший квестором на Сицилии в 75 году до н. э., пишет в «Тускуланских беседах» (книга V), что ему в 75 году до н. э., спустя 137 лет после этих событий, удалось обнаружить полуразрушенную могилу Архимеда; на ней, как и завещал Архимед, было изображение шара, вписанного в цилиндр.
Слайд 14Научная деятельность
По словам Плутарха, Архимед был просто одержим
математикой. Он забывал о пище, совершенно не заботился о себе.
Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призм и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. Идеи Архимеда легли впоследствии в основу интегрального исчисления.
Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3.
Лучшим своим достижением он считал определение поверхности и объёма шара — задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.
Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида , корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призм и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. Идеи Архимеда легли впоследствии в основу интегрального исчисления.
Архимед сумел установить, что сфера и конусы с общей вершиной, вписанные в цилиндр, соотносятся следующим образом: два конуса : сфера : цилиндр как 1:2:3.
Лучшим своим достижением он считал определение поверхности и объёма шара — задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.
Слайд 16
Задача о делении угла на три равные части возникла из потребностей
архитектуры и строительной техники. При составлении рабочих чертежей, разного рода украшений, многогранных колоннад, при строительстве, внутренней и внешней отделки храмов, надгробных памятников древние инженеры, художники встретились с необходимостью уметь делить окружность на три равные части, а это часто вызывало затруднения. Оригинальное и вместе с тем чрезвычайно простое решение задачи о трисекции угла дал Архимед.
Слайд 17Измерение круга
Задача о квадратуре круга заключается в
следующем: построить квадрат, площадь которого была бы равна площади данного круга. Большой вклад в решение этой задачи внес Архимед. В своем трактате "Измерение круга" он доказывает следующие три теоремы:
Теорема первая: Площадь круга равна площади прямоугольного треугольника, один из катетов которого равняется длине окружности круга, а другой радиусу круга.
Теорема вторая: Площадь круга относится к площади квадрата, построенного на диаметре, приблизительно, как 11:14.
Теорема третья: C-3d < d и C-3d > d, где С -длина окружности, а d-ее диаметр. Откуда, d < C-3d < d. Верхнюю и нижнюю границы для числа Архимед получил путем последовательного рассмотрения отношений периметров к диаметру правильных описанных и вписанных в круг многоугольников, начиная с шестиугольника и кончая 96-угольником. Если приравнять верхней границе, то получим архимедово значение (архимедово число).
Теорема первая: Площадь круга равна площади прямоугольного треугольника, один из катетов которого равняется длине окружности круга, а другой радиусу круга.
Теорема вторая: Площадь круга относится к площади квадрата, построенного на диаметре, приблизительно, как 11:14.
Теорема третья: C-3d < d и C-3d > d, где С -длина окружности, а d-ее диаметр. Откуда, d < C-3d < d. Верхнюю и нижнюю границы для числа Архимед получил путем последовательного рассмотрения отношений периметров к диаметру правильных описанных и вписанных в круг многоугольников, начиная с шестиугольника и кончая 96-угольником. Если приравнять верхней границе, то получим архимедово значение (архимедово число).
Слайд 18Архимед физик
Архимеда справедливо считают основоположником математической физики.
С его именем связывается введение понятия центра тяжести, открытие законов рычага и разработка основ гидростатики. Известно, что он занимался и геометрической оптикой, хотя его работы в этой области до нас не дошли. Для древних греков физика была целостным учением о мире и считалась частью философии. Ее практические стороны, такие, как механика, относились к прикладным дисциплинам. Математика хотя и применялась, но от нее не требовали ни строгости, ни полноты описания явлений.
Архимед первым подошел к решению физических задач с широким применением математики. Как уже говорилось, он начал с механики. Античные механические представления настолько отличались от наших, что сейчас воспринимаются с трудом, хотя «Физику» Аристотеля (384...322 г. до н.э.) в течение многих столетий изучали, комментировали, считали безошибочной. Аристотель разделял движения на «естественные» и «насильственные». Естественным считалось стремление материи к своему «месту», зависящему от ее свойств, например стремление камня к центру ; Земли, огня – от Земли вверх. Насильственные движения предполагали внешнюю причину – приложение силы. Механика Аристотеля не знала явления инерции: движение должно было прекратиться тотчас же после прекращения действия силы. Движение же по инерции объяснялось влиянием среды. Так, последователи Аристотеля считали, что при бросании камня возникает воздушный вихрь, несущий его после того, как камень покинул руку.
В своих трудах Архимед изучал только силы, которые с точки зрения аристотелевой механики вызывают «естественные» движения. Более того, он сразу упростил задачу, исключив из нее движение. Так появилась статика.
Архимед первым подошел к решению физических задач с широким применением математики. Как уже говорилось, он начал с механики. Античные механические представления настолько отличались от наших, что сейчас воспринимаются с трудом, хотя «Физику» Аристотеля (384...322 г. до н.э.) в течение многих столетий изучали, комментировали, считали безошибочной. Аристотель разделял движения на «естественные» и «насильственные». Естественным считалось стремление материи к своему «месту», зависящему от ее свойств, например стремление камня к центру ; Земли, огня – от Земли вверх. Насильственные движения предполагали внешнюю причину – приложение силы. Механика Аристотеля не знала явления инерции: движение должно было прекратиться тотчас же после прекращения действия силы. Движение же по инерции объяснялось влиянием среды. Так, последователи Аристотеля считали, что при бросании камня возникает воздушный вихрь, несущий его после того, как камень покинул руку.
В своих трудах Архимед изучал только силы, которые с точки зрения аристотелевой механики вызывают «естественные» движения. Более того, он сразу упростил задачу, исключив из нее движение. Так появилась статика.
Слайд 19Оптика
В своем стремлении математически описать явления природы
Архимед выделял задачи, наиболее поддающиеся геометрическому анализу. Поэтому занятия Архимеда в области геометрической оптики – «катоптрике», как ее называли прежде, можно считать закономерными.
Очень немного можно сказать о «катоптрике» Архимеда. От нее в позднем пересказе уцелела единственная теорема, в которой доказывается, что при отражении света от зеркала угол падения луча равен углу отражения. Свои оптические теории (как и механические) Архимед строил на основе аксиом. Одной из таких аксиом являлась обратимость хода луча – глаз и объект наблюдения можно поменять местами. Весь же круг вопросов «катоптрики» был очень широк. Перечисление проблем, которых касался Архимед в этой книге, мы находим у других авторов античного периода. Вот как об этих работах говорил Апулей: «Почему в плоских зеркалах предметы сохраняют свою натуральную величину, в выпуклых – уменьшаются, а в вогнутых – увеличиваются; почему левые части предметов видны справа и наоборот; когда изображение в зеркале исчезает и когда появляется; почему вогнутые зеркала, будучи поставлены против Солнца, зажигают поднесенный к ним трут; почему в небе видна радуга; почему иногда кажется, что на небе два одинаковых Солнца, и много другого подобного же рода, о чем рассказывается в объемистом томе Архимеда». Из других свидетельств следует, что Архимед изучал также и явление преломления лучей в воде.
С «катоптрикой» связана легенда о поджоге Архимедом римских кораблей во время осады Сиракуз. Что в ней вымысел и что, быть может, является отражением действительных событий, мы рассмотрим в отдельной главе.
Можно не сомневаться в том, что «катоптрика» Архимеда оказала большое влияние на последующее развитие оптики.
Очень немного можно сказать о «катоптрике» Архимеда. От нее в позднем пересказе уцелела единственная теорема, в которой доказывается, что при отражении света от зеркала угол падения луча равен углу отражения. Свои оптические теории (как и механические) Архимед строил на основе аксиом. Одной из таких аксиом являлась обратимость хода луча – глаз и объект наблюдения можно поменять местами. Весь же круг вопросов «катоптрики» был очень широк. Перечисление проблем, которых касался Архимед в этой книге, мы находим у других авторов античного периода. Вот как об этих работах говорил Апулей: «Почему в плоских зеркалах предметы сохраняют свою натуральную величину, в выпуклых – уменьшаются, а в вогнутых – увеличиваются; почему левые части предметов видны справа и наоборот; когда изображение в зеркале исчезает и когда появляется; почему вогнутые зеркала, будучи поставлены против Солнца, зажигают поднесенный к ним трут; почему в небе видна радуга; почему иногда кажется, что на небе два одинаковых Солнца, и много другого подобного же рода, о чем рассказывается в объемистом томе Архимеда». Из других свидетельств следует, что Архимед изучал также и явление преломления лучей в воде.
С «катоптрикой» связана легенда о поджоге Архимедом римских кораблей во время осады Сиракуз. Что в ней вымысел и что, быть может, является отражением действительных событий, мы рассмотрим в отдельной главе.
Можно не сомневаться в том, что «катоптрика» Архимеда оказала большое влияние на последующее развитие оптики.
Слайд 21
Архимедов винт, винт Архимеда — механизм, исторически использовавшийся для передачи воды из низколежащих водоёмов
в оросительные каналы. Он был одним из нескольких изобретений и открытий, традиционно приписываемых Архимеду, жившему в III веке до н. э. Архимедов винт стал прообразом шнека.
Слайд 22Принцип работы
Машина состоит из винта внутри полой трубы. Она
была изобретена Архимедом примерно в 250 году до н. э. либо в Греции ранее. Винт можно представить как наклонную плоскость, навёрнутую на цилиндр.
Винт вращается обычно с помощью ветряного колела либо вручную. В то время, как поворачивается нижний конец трубы, он собирает некоторый объём воды. Это количество воды будет скользить вверх по спиральной трубе во время вращения вала, пока наконец вода не выльется из вершины трубы, снабжая ирригационную систему.
Контактная поверхность между винтом и трубой не обязана быть идеально водонепроницаемой, потому что относительно большое количество воды черпается за один поворот по отношению к угловой скорости винта. Кроме того, вода, просачивающаяся из верхней секции винта, попадает в предыдущую секцию и так далее, таким образом, в машине достигается динамическое равновесие, что препятствует уменьшению механической эффективности.
«Винт» не обязан поворачиваться внутри неподвижной оболочки, он может вращаться вместе с нею как одно целое. Винт может быть герметично прикреплён с помощью смолы или другого связующего к оболочке либо отлит из бронзы как одно целое с оболочкой, как, по предположению некоторых исследователей, были сделаны устройства, орошавшие висячие сады в Вавилоне. Изображения древнегреческих и древнеримских водяных винтов показывают, что винт двигался человеком, наступавшим на внешнюю оболочку, чтобы вращать весь аппарат как единое целое, что требовало, чтобы корпус был жестко скреплён с винтом.
Винт вращается обычно с помощью ветряного колела либо вручную. В то время, как поворачивается нижний конец трубы, он собирает некоторый объём воды. Это количество воды будет скользить вверх по спиральной трубе во время вращения вала, пока наконец вода не выльется из вершины трубы, снабжая ирригационную систему.
Контактная поверхность между винтом и трубой не обязана быть идеально водонепроницаемой, потому что относительно большое количество воды черпается за один поворот по отношению к угловой скорости винта. Кроме того, вода, просачивающаяся из верхней секции винта, попадает в предыдущую секцию и так далее, таким образом, в машине достигается динамическое равновесие, что препятствует уменьшению механической эффективности.
«Винт» не обязан поворачиваться внутри неподвижной оболочки, он может вращаться вместе с нею как одно целое. Винт может быть герметично прикреплён с помощью смолы или другого связующего к оболочке либо отлит из бронзы как одно целое с оболочкой, как, по предположению некоторых исследователей, были сделаны устройства, орошавшие висячие сады в Вавилоне. Изображения древнегреческих и древнеримских водяных винтов показывают, что винт двигался человеком, наступавшим на внешнюю оболочку, чтобы вращать весь аппарат как единое целое, что требовало, чтобы корпус был жестко скреплён с винтом.
Слайд 24Применение
Издавна архимедов винт применялся для подъёма воды
в оросительные каналы. Кроме того, это устройство также использовалось для «кражи» земли у моря в Голландии и других местах при создании польдеров. Часть моря перекрывалась дамбой, и вода удалялась из огороженного участка, начиная процесс осушения земли для использования в земледелии. В зависимости от длины и диаметра винтов, более чем одна машина могли использоваться, чтобы успешно поднять ту же самую воду.
Архимедовы винты использовались в установках по обработке сточных вод, потому что они успешно справляются с разными мощностями потока и с суспензиями.
Тот же принцип можно увидеть в пескалаторах, которые являются архимедовыми винтами, предназначенными для безопасного подъёма рыбы из прудов и перевозки её в другое место. Эта технология в основном применяется на рыбоводных заводах (рыбопитомниках), где она предпочтительна для уменьшения грубого обращения с рыбой.
Архимедовы винты использовались в установках по обработке сточных вод, потому что они успешно справляются с разными мощностями потока и с суспензиями.
Тот же принцип можно увидеть в пескалаторах, которые являются архимедовыми винтами, предназначенными для безопасного подъёма рыбы из прудов и перевозки её в другое место. Эта технология в основном применяется на рыбоводных заводах (рыбопитомниках), где она предпочтительна для уменьшения грубого обращения с рыбой.
Слайд 25Спираль Архимеда
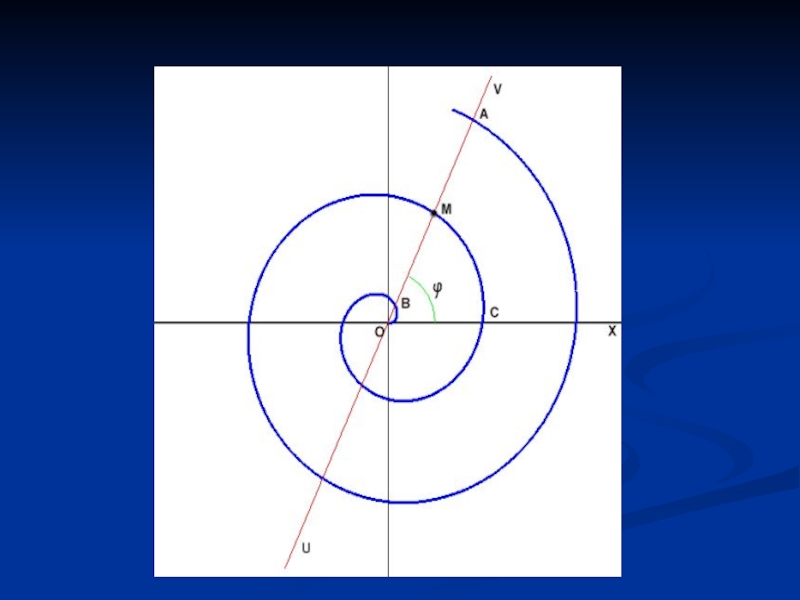
Архимедова спираль — спираль, плоская кривая, траектория точки M , которая равномерно движется вдоль луча OV с началом
в O, в то время как сам луч OV равномерно вращается вокруг O. Другими словами, расстояние ρ = OM пропорционально углу поворота φ луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение p.
Слайд 28
Действительно ли хитроумный грек мог накормить рыб
в море около Сиракуз жареными римлянами? Этот миф проверялся несколько раз — причем с неодинаковыми результатами. Наиболее интересным оказался эксперимент Массачусетского технологического института, проведенный в 2005 году.
Древние источники описывают конструкцию архимедова «гиперболоида» очень противоречиво — то ли это были бронзовые щиты, то ли гигантский отражатель. Исследователи предположили, что Архимед вряд ли мог изготовить огромный (а потому очень уязвимый) рефлектор, и выбрали вариант со щитами, заменив их на 127 зеркал размером примерно 30 на 30 сантиметров.
Экспериментаторы не ставили целью полностью воссоздать условия применения «гиперболоида». Макет корабля был сделан из твердого дуба, хотя для изготовления римских судов использовались более горючие сорта древесины — например, кипарис. Корабельные борта были сухими, хотя в реальности они открыты волнам. Расстояние до цели — 30 метров, но на самом деле оно было гораздо больше (как минимум — дистанция полета стрелы). Кроме того, макет оставался неподвижным, а римские корабли слегка перемещались, даже стоя на якоре в бухте Сиракуз.
Древние источники описывают конструкцию архимедова «гиперболоида» очень противоречиво — то ли это были бронзовые щиты, то ли гигантский отражатель. Исследователи предположили, что Архимед вряд ли мог изготовить огромный (а потому очень уязвимый) рефлектор, и выбрали вариант со щитами, заменив их на 127 зеркал размером примерно 30 на 30 сантиметров.
Экспериментаторы не ставили целью полностью воссоздать условия применения «гиперболоида». Макет корабля был сделан из твердого дуба, хотя для изготовления римских судов использовались более горючие сорта древесины — например, кипарис. Корабельные борта были сухими, хотя в реальности они открыты волнам. Расстояние до цели — 30 метров, но на самом деле оно было гораздо больше (как минимум — дистанция полета стрелы). Кроме того, макет оставался неподвижным, а римские корабли слегка перемещались, даже стоя на якоре в бухте Сиракуз.
Слайд 31
Итальянская группа учёных под руководством Чезаре Росси
произвела расчёты и даже дорогие опыты, которые показали, что паровая пушка Архимеда могла вести огонь по противнику тяжеловесными ядрами. Огневая мощь этой пушки, если применять для нее ядра весом в 13 футов (6 килограммов), могла составлять 134 мили в час (214 км/час), или 60 метров в секунду. Такие показатели пушки приводили в ужас современников. Ведь паровая пушка давала греческим войскам возможность поливать огнём римский флот и полки с расстояния 500 футов (150 метров). К тому же пушка Архимеда отличалась идеальной меткостью и лёгкостью наводки. Стоило только запустить в противника «пробный шар», а дальше канонир мог наводить прицел, исходя из знаний геометрии Архимеда. Чезаре Росси считает, что плоская траектория полёта ядра позволяла делать точность попадания ядер почти идеальной. Уже сам громобойный залп такой пушки мог вызвать панику в рядах противника, воспринимавших его как гром и кару небесные.
Слайд 32Закон Архимеда
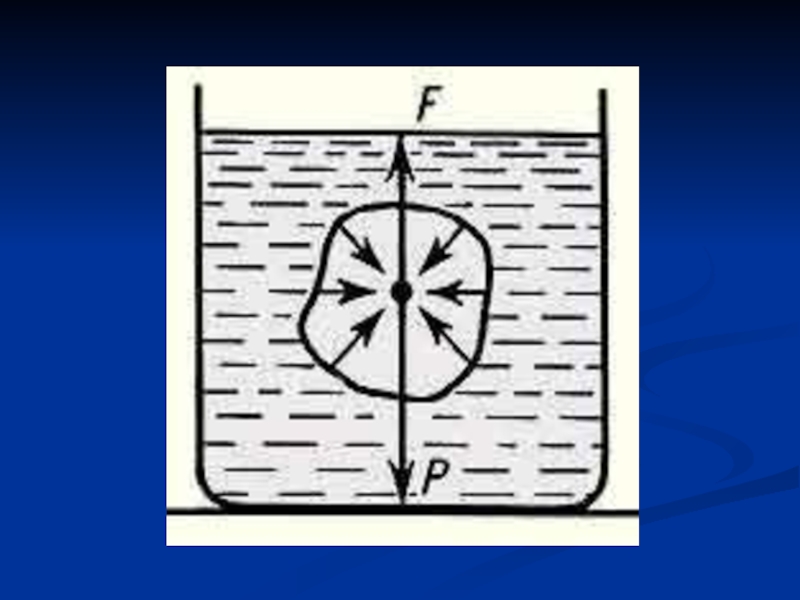
Закон Архимеда: на всякое тело, погруженное в жидкость, действует выталкивающая
сила, направленная вверх и равная весу вытесненной им жидкости. Закон Архимеда справедлив и для газов.
F — выталкивающая сила;
P — сила тяжести, действующая на тело.
F — выталкивающая сила;
P — сила тяжести, действующая на тело.
Слайд 34Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от
соотношения между модулями силы тяжести и силы Архимеда , которые действуют на это тело. Возможны следующие три случая:
— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнет плавать.
Другая формулировка (где — плотность тела, — плотность среды, в которую оно погружено):
— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнет плавать.
— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнет плавать.
Другая формулировка (где — плотность тела, — плотность среды, в которую оно погружено):
— тело тонет;
— тело плавает в жидкости или газе;
— тело всплывает до тех пор, пока не начнет плавать.
Слайд 35История развития подводных лодок
Принято считать, что первую
подводную лодку построил и испытал на Темзе в 1620 г. голландский механик и физик Корнелий Ван-Дреббель. Его деревянная лодка, обтянутая снаружи промасленной кожей, могла перемещаться с помощью весел в подводном положении на небольшие расстояния. Экипаж состоял из двенадцати гребцов и трех офицеров. Хроника свидетельствует, что при погружении лодки на глубину присутствовал сам король Яков I. Исследователи не исключают использование Ван-Дреббелем сжатого воздуха, а может быть, даже и кислорода. Они так и писали: “Судно могло находиться под водой в течение нескольких часов на глубине от 4 до 5 метров. Начатые опыты прервала смерть Ван-Дреббеля". В год его кончины, то есть в 1634 г., французский ученый, математик и философ Сарен Мерсенн издал книгу, которая помогла многим поколениям строителей подводных судов практическими советами, Мерсенн, например, советовал строить подводные лодки, формой похожие на рыб, а оба конца их корпуса делать одинаково заостренными. Материалом, пригодным для постройки, Мерсенн считал медь, а не дерево и рекомендовал не увлекаться размерами судов.
Слайд 37
В 1834 г. на Александровском литейном заводе
в Петербурге по проекту военного инженера К. А. Шильдера была построена подводная лодка, вооруженная пусковыми ракетными установками (по три с каждого борта). Лодка двигалась при помощи четырех специальных гребков, устроенных по принципу утиных лапок и расположенных попарно на каждом борту вне корпуса. Они приводились в действие матросами-гребцами, но скорость подводного хода (при неимоверных усилиях экипажа) не превышала полукилометра в час. Шильдер надеялся перевести гребки на электродвижение, однако прогресс в электротехнике в те годы был слишком медленным, и осенью 1841 г. дальнейшие работы по совершенствованию лодки были прекращены.
Слайд 39
Лишь в 1884 г. русский изобретатель С.
К. Джевецкий добился успеха, установив на подводной лодке своей конструкции электродвигатель мощностью в 1 л. с. с новым в то время источником электрической энергии - аккумуляторной батареей. На испытаниях лодка шла под водой против течения Невы со скоростью 4 узла. Это была первая в мире подводная лодка с электродвижением.
Джевецкий был и автором проекта подводной лодки “Почтовый", которая вошла в историю как первый подводный корабль с единым двигателем. Эта лодка, заложенная на стапеле Металлического завода в Петербурге в 1906 г., при длине 36,0 и ширине 3,2 м имела подводное водоизмещение 146 т. На ней были установлены два бензиновых мотора мощностью по 130 л. с., работавших через зубчатую передачу на один гребной вал. При работе обоих двигателей скорость лодки в надводном положении достигала 11,5 узла. На подводной лодке имелось также 45 баллонов сжатого воздуха с давлением до 200 атмосфер. Через сложную систему подачи воздух поступал к одному из двигателей и обеспечивал кораблю подводный ход более 6 узлов. Выхлопные газы выбрасывались в водонепроницаемую выгородку в надстройке, откуда откачивались за борт. Дальность плавания лодки под водой составляла 28 миль. На испытаниях она показала неплохие результаты, но ее основной недостаток - пузырчатый след при движении под водой - демаскировал корабль и делал его малопригодным для военных целей.
Джевецкий был и автором проекта подводной лодки “Почтовый", которая вошла в историю как первый подводный корабль с единым двигателем. Эта лодка, заложенная на стапеле Металлического завода в Петербурге в 1906 г., при длине 36,0 и ширине 3,2 м имела подводное водоизмещение 146 т. На ней были установлены два бензиновых мотора мощностью по 130 л. с., работавших через зубчатую передачу на один гребной вал. При работе обоих двигателей скорость лодки в надводном положении достигала 11,5 узла. На подводной лодке имелось также 45 баллонов сжатого воздуха с давлением до 200 атмосфер. Через сложную систему подачи воздух поступал к одному из двигателей и обеспечивал кораблю подводный ход более 6 узлов. Выхлопные газы выбрасывались в водонепроницаемую выгородку в надстройке, откуда откачивались за борт. Дальность плавания лодки под водой составляла 28 миль. На испытаниях она показала неплохие результаты, но ее основной недостаток - пузырчатый след при движении под водой - демаскировал корабль и делал его малопригодным для военных целей.
Слайд 40Влияние работ Архимеда на развитие физики
Если говорить
об ученых, опередивших свое время, то Архимед, вероятно, может считаться своеобразным рекордсменом. Его идеи нашли продолжателей лишь через 1800 лет.
Предложенное Архимедом направление в науке – математическая физика, которую он провозгласил и в которой так много сделал, не была воспринята ни его ближайшими потомками, ни учеными средневековья.
Архимеда знали как гениального математика, им восхищались, его изучали и комментировали, но его физические работы долгое время не получали развития.
В какой-то мере в средние века на сочинениях Архимеда базировались работы ряда ученых Востока о взвешивании и определении удельного веса веществ. Математик и астроном IX в. Сабит ибн-Корра перевел на арабский язык и прокомментировал многие сочинения Архимеда и составил трактат о рычажных весах. На основе сочинения Архимеда «О плавающих телах» крупнейшие ученые того же времени ал-Бируни и Омар Хайям провели определения удельных весов большого количества металлов и драгоценных камней. При этом ал-Бируни пользовался методом сравнения значений веса равных объемов различных минералов, а Омар Хайям – методом взвешивания образцов на воздухе и в воде.
Предложенное Архимедом направление в науке – математическая физика, которую он провозгласил и в которой так много сделал, не была воспринята ни его ближайшими потомками, ни учеными средневековья.
Архимеда знали как гениального математика, им восхищались, его изучали и комментировали, но его физические работы долгое время не получали развития.
В какой-то мере в средние века на сочинениях Архимеда базировались работы ряда ученых Востока о взвешивании и определении удельного веса веществ. Математик и астроном IX в. Сабит ибн-Корра перевел на арабский язык и прокомментировал многие сочинения Архимеда и составил трактат о рычажных весах. На основе сочинения Архимеда «О плавающих телах» крупнейшие ученые того же времени ал-Бируни и Омар Хайям провели определения удельных весов большого количества металлов и драгоценных камней. При этом ал-Бируни пользовался методом сравнения значений веса равных объемов различных минералов, а Омар Хайям – методом взвешивания образцов на воздухе и в воде.
Слайд 41
В эпоху Возрождения, когда центр научной мысли
вновь переместился в Европу, европейская наука училась у арабской. Некоторые труды Архимеда дошли до нас только в арабских переводах. Одним из первых продолжателей механики Архимеда был итальянский ученый и инженер Гвидо Убальди дель Монте (1545...1607), исследовавший вопросы равновесия и решивший задачу о грузе на наклонной плоскости. Многое сделал для развития статики Архимеда другой итальянский ученый – Джовани Баттиста Бенедетти (1530...1590). Крупнейшим механиком «школы Архимеда» был фламандский ученый Симон Стевин (1548...1620). В своем классическом труде «Начала статики» он не только исходит из ряда аксиом Архимеда, но и развивает его работы, анализируя целый ряд механизмов. В число постулатов Стевин вводит принцип невозможности вечного двигателя; ему принадлежит также введение обозначений сил в виде стрелок. Много Стевин сделал и в области гидростатики, развив положения Архимеда, данные им в «Плавающих телах». Интерес Стевина к этим проблемам был далеко не абстрактным, так как он занимал должность инспектора плотин и консультанта голландского адмиралтейства.
Главным достижением классической механики была математическая разработка законов динамики Галилеем и Ньютоном. И хотя здесь достижения Архимеда непосредственно не использовались, его математический подход к проблемам торжествовал. Знаменательно, что Галилей хорошо знал труды Архимеда и часто к ним обращался. Например, при рассмотрении |равноускоренного движения он писал: «Я не предполагаю ничего иного, кроме определения движения; я хочу трактовать и рассматривать это явление в подражание Архимеду, который, заявив в «Спиральных линиях», что под движением по спирали он понимает движение, слагающееся из двух равномерных (одного – прямолинейного, а другого – кругового), непосредственно переходит к демонстрации выводов. Я заявляю о намерении исследовать признаки, присущие движению тела, начинающемуся с состояния покоя и продолжающемуся с равномерно возрастающей скоростью, а именно так, что приращения этой скорости возрастают не скачками, а плавно, пропорционально времени».
Главным достижением классической механики была математическая разработка законов динамики Галилеем и Ньютоном. И хотя здесь достижения Архимеда непосредственно не использовались, его математический подход к проблемам торжествовал. Знаменательно, что Галилей хорошо знал труды Архимеда и часто к ним обращался. Например, при рассмотрении |равноускоренного движения он писал: «Я не предполагаю ничего иного, кроме определения движения; я хочу трактовать и рассматривать это явление в подражание Архимеду, который, заявив в «Спиральных линиях», что под движением по спирали он понимает движение, слагающееся из двух равномерных (одного – прямолинейного, а другого – кругового), непосредственно переходит к демонстрации выводов. Я заявляю о намерении исследовать признаки, присущие движению тела, начинающемуся с состояния покоя и продолжающемуся с равномерно возрастающей скоростью, а именно так, что приращения этой скорости возрастают не скачками, а плавно, пропорционально времени».
Слайд 55Заключение
Если окинуть взглядом разнообразную и плодотворную работу Архимеда, может показаться,
что в своей деятельности ученый «разбрасывался», увлекаясь различными, не связанными между собой проблемами. Но несмотря на разнообразие задач, за которые брался Архимед, можно заметить между ними определенную связь. Например, занимаясь проблемами равновесия, Архимед выполнил целую серию работ, связанных с применением открытых им закономерностей. Придя к понятию центра тяжести при разработке методов строительных расчетов, он построил геометрическую теорию нахождения центров тяжести фигур и дал строгую формулировку законов равновесия. Разработанную теорию он применил на практике, создав многоступенчатые механические передачи и «железные лапы». Но эту же теорию он применил и в геометрии, решив с помощью «мысленного взвешивания» задачу об определении площади сложных фигур.
Геометрическое сочинение Архимеда «О спиралях» (в котором, кстати, впервые вводится кинематическое описание кривой) связано с созданием водоподъемной «улитки» (гидравлика) и червячной передачи (механика).
Таким образом, главным в творчестве Архимеда было стремление максимально раздвинуть рамки задачи вширь, одновременно доведя ее решение до геометрической строгости.
Геометрическое сочинение Архимеда «О спиралях» (в котором, кстати, впервые вводится кинематическое описание кривой) связано с созданием водоподъемной «улитки» (гидравлика) и червячной передачи (механика).
Таким образом, главным в творчестве Архимеда было стремление максимально раздвинуть рамки задачи вширь, одновременно доведя ее решение до геометрической строгости.
Слайд 56
В астрономии Архимед предстает перед нами и как наблюдатель (определение
видимого поперечника Солнца), и как теоретик (приведение результатов измерений к центру Земли), и как вычислитель (расчет межпланетных расстояний), и как механик (создание небесного глобуса). Теоретические занятия законами отражения света, возможно, привели к изобретению и постройке гелиоконцентратора, причем сама идея расчленения вогнутого зеркала на множество плоских элементов связана с заменой кривой вписанными и описанными многоугольниками, часто применявшейся Архимедом в геометрических доказательствах.
Такое сочетание математического таланта с практическим мышлением и организаторскими способностями встречается не так уж часто. Архимед является в истории науки яркой фигурой исследователя, слившего воедино теорию и практику, и он несомненно служил образцом и примером для многих поколений ученых.
Интересной особенностью характера Архимеда было его пристрастие к большим масштабам.
Архимед не был замкнутым ученым. Он стремился сделать свои достижения общеизвестными. Его любовь к эффектным демонстрациям хорошо проявлялась в эпизоде с передвижением вытащенного на берег корабля «силой одного человека». Видимо, и шедевр античной механики – небесный глобус – не имел другого назначения, кроме демонстрационного. Среди научных работ Архимеда есть и популяризаторская – «Псаммит». Об
этом говорит и сама постановка задачи, и то, что система записи крупных чисел к этому времени уже была описана Архимедом в другой не дошедшей до нас книге.
Таким предстает перед нами Архимед – теоретик, исследователь, инженер, популяризатор науки.
Такое сочетание математического таланта с практическим мышлением и организаторскими способностями встречается не так уж часто. Архимед является в истории науки яркой фигурой исследователя, слившего воедино теорию и практику, и он несомненно служил образцом и примером для многих поколений ученых.
Интересной особенностью характера Архимеда было его пристрастие к большим масштабам.
Архимед не был замкнутым ученым. Он стремился сделать свои достижения общеизвестными. Его любовь к эффектным демонстрациям хорошо проявлялась в эпизоде с передвижением вытащенного на берег корабля «силой одного человека». Видимо, и шедевр античной механики – небесный глобус – не имел другого назначения, кроме демонстрационного. Среди научных работ Архимеда есть и популяризаторская – «Псаммит». Об
этом говорит и сама постановка задачи, и то, что система записи крупных чисел к этому времени уже была описана Архимедом в другой не дошедшей до нас книге.
Таким предстает перед нами Архимед – теоретик, исследователь, инженер, популяризатор науки.