- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Электротехника на тему Электрические цепи переменного тока
Содержание
- 1. Презентация по дисциплине Электротехника на тему Электрические цепи переменного тока
- 2. Основные понятия и определения Переменным током называют такой
- 3. Переменный ток имеет ряд преимуществ по сравнению
- 4. Если поместить металлическую рамку в равномерное магнитное
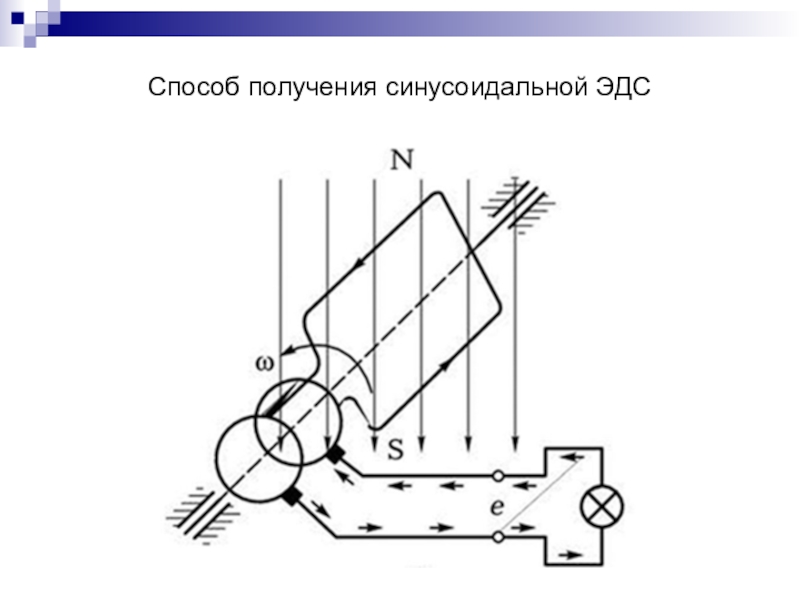
- 5. Способ получения синусоидальной ЭДС
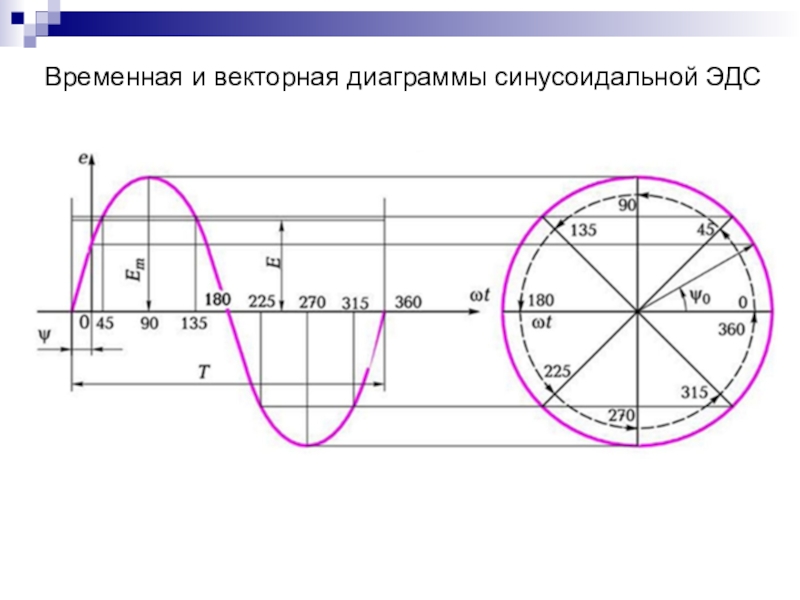
- 6. Временная и векторная диаграммы синусоидальной ЭДС
- 7. Величина промышленной частоты переменного тока обусловлена технико-экономическими
- 8. Для описания характеристик переменного тока необходимо избрать
- 9. Действующими значениями тока и напряжения называют соответствующие
- 10. Шкалы измерительных приборов переменного тока отградуированы в
- 11. Таким образом, в ЭЦ переменного тока следует
- 12. В линейных цепях синусоидальная ЭДС создает синусоидальный
- 13. Векторные диаграммыПоскольку синусоидальная функция определяется амплитудой и
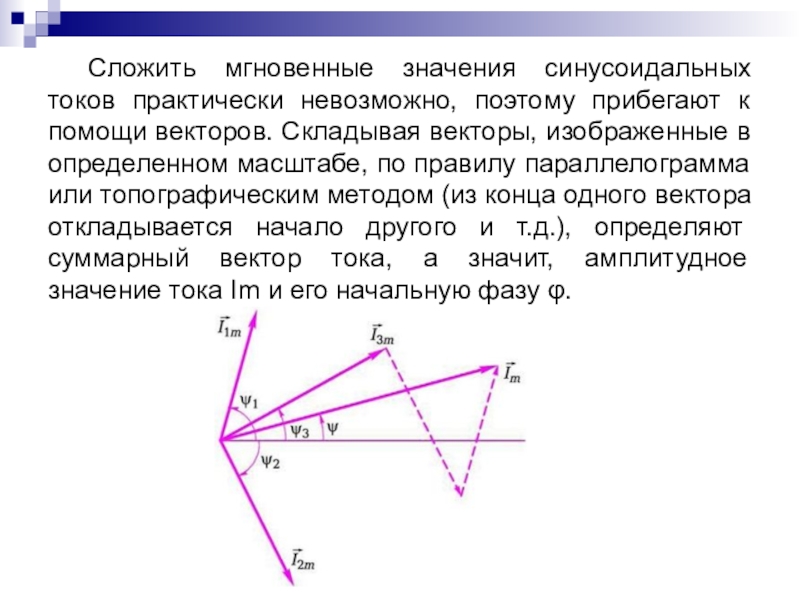
- 14. Сложить мгновенные значения синусоидальных токов практически невозможно,
- 15. Мгновенное значение результирующего тока в этом случае
Основные понятия и определения Переменным током называют такой ток, который периодически изменяет и величину, и направление. Цепи с периодически изменяющимся во времени током называются электрическими цепями переменного тока. До конца 19 века использовались только источники постоянного тока -
Слайд 2Основные понятия и определения
Переменным током называют такой ток, который периодически изменяет
и величину, и направление. Цепи с периодически изменяющимся во времени током называются электрическими цепями переменного тока.
До конца 19 века использовались только источники постоянного тока - химические элементы и генераторы. Это ограничивало возможности передачи эл. энергии на большие расстояния. Так как для уменьшения потерь в линиях электропередачи необходимо использовать высокое напряжение. Однако получить высокое напряжение от генератора постоянного тока невозможно. Проблема была решена только при использовании переменного тока и трансформаторов.
До конца 19 века использовались только источники постоянного тока - химические элементы и генераторы. Это ограничивало возможности передачи эл. энергии на большие расстояния. Так как для уменьшения потерь в линиях электропередачи необходимо использовать высокое напряжение. Однако получить высокое напряжение от генератора постоянного тока невозможно. Проблема была решена только при использовании переменного тока и трансформаторов.
Слайд 3 Переменный ток имеет ряд преимуществ по сравнению с постоянным:
генератор переменного
тока значительно проще и дешевле генератора постоянного тока;
переменный ток можно трансформировать;
переменный ток легко преобразуется в постоянный;
двигатели переменного тока значительно проще и дешевле, чем двигатели постоянного тока.
Наибольшее промышленное применение получили цепи синусоидального тока, величина которого изменяется по закону синуса. Это обусловлено достаточно простым способом получения синусоидального тока, а также более высоким КПД генераторов, двигателей, трансформаторов, линий передач при работе на синусоидальном токе по сравнению с несинусоидальным.
переменный ток можно трансформировать;
переменный ток легко преобразуется в постоянный;
двигатели переменного тока значительно проще и дешевле, чем двигатели постоянного тока.
Наибольшее промышленное применение получили цепи синусоидального тока, величина которого изменяется по закону синуса. Это обусловлено достаточно простым способом получения синусоидального тока, а также более высоким КПД генераторов, двигателей, трансформаторов, линий передач при работе на синусоидальном токе по сравнению с несинусоидальным.
Слайд 4 Если поместить металлическую рамку в равномерное магнитное поле (рис.1, а) и
вращать ее с частотой Ѡ, то в ней в соответствии с законом электромагнитной индукции будет наводиться переменная ЭДС (рис. 1, б):
е=Em *sin (Ѡt + φ ),
где е — мгновенное значение ЭДС, В;
Еm — амплитудное значение ЭДС, В;
Ѡ— угловая частота (угловая скорость), рад/с (радиан в секунду);
φ — начальная фаза, определяющая значение е (ЭДС), рад;
sin (Ѡt + φ ) — текущее значение фазы, рад.
При этом угловая частота Ѡ= 2πf= 2π/Т, где f - линейная частота, Гц; Т-период колебаний, сек.
е=Em *sin (Ѡt + φ ),
где е — мгновенное значение ЭДС, В;
Еm — амплитудное значение ЭДС, В;
Ѡ— угловая частота (угловая скорость), рад/с (радиан в секунду);
φ — начальная фаза, определяющая значение е (ЭДС), рад;
sin (Ѡt + φ ) — текущее значение фазы, рад.
При этом угловая частота Ѡ= 2πf= 2π/Т, где f - линейная частота, Гц; Т-период колебаний, сек.
Слайд 7 Величина промышленной частоты переменного тока обусловлена технико-экономическими соображениями. Если она слишком
низка, то увеличиваются габариты электрических машин и, следовательно, расход материалов на их изготовление; заметным становится мигание света в электрических лампочках.
При слишком высоких частотах увеличиваются потери энергии в сердечниках электрических машин и трансформаторах.
Поэтому наиболее оптимальными оказались частоты 50-60 Гц. Однако в некоторых случаях используются переменные токи как с более высокой, так и с более низкой частотой. Например, в самолетах применяется частота 400 Гц. На этой частоте можно значительно уменьшить габариты и вес трансформаторов и электромоторов, что для авиации более существенно, чем увеличение потерь в сердечниках. На железных дорогах используют переменный ток с частотой 25 Гц.
При слишком высоких частотах увеличиваются потери энергии в сердечниках электрических машин и трансформаторах.
Поэтому наиболее оптимальными оказались частоты 50-60 Гц. Однако в некоторых случаях используются переменные токи как с более высокой, так и с более низкой частотой. Например, в самолетах применяется частота 400 Гц. На этой частоте можно значительно уменьшить габариты и вес трансформаторов и электромоторов, что для авиации более существенно, чем увеличение потерь в сердечниках. На железных дорогах используют переменный ток с частотой 25 Гц.
Слайд 8 Для описания характеристик переменного тока необходимо избрать определенные физические величины. Мгновенные
и амплитудные значения для этих целей неудобны, а средние значения за период равны нулю. К тому же расчет цепей с использованием мгновенных значений синусоидальных ЭДС, токов и напряжений достаточно сложен, поэтому мгновенные значения заменяют действующими значениями. Поэтому вводят понятие действующих значений тока и напряжения. На рис. - Е — действующее значение ЭДС, В.
Они основаны на тепловом действии тока, не зависящем от его направления.
Они основаны на тепловом действии тока, не зависящем от его направления.
Слайд 9 Действующими значениями тока и напряжения называют соответствующие параметры такого постоянного тока,
при котором в данном проводнике за данный промежуток времени выделяется столько же теплоты, что и при реальном переменном токе.
При изменении тока по синусоиде его действующее значение меньше его амплитудного значения в √2 раз, т. е. I= (Im/√2) =0,707*Im.
Если синусоидальный ток i нагревает проводник, например, до температуры 100 °С, то постоянный ток, значение которого равно амплитуде синусоидального (Iп = Im), нагреет тот же проводник сильнее. Чтобы нагреть проводник постоянным током до тех же 100 °С, необходимо значение тока уменьшить до I=(Im/√2) =0,707*Im. Такое же значение будет справедливо и для U = Um/√2. В некоторых источниках действующие значения называют эффективными значениями.
При изменении тока по синусоиде его действующее значение меньше его амплитудного значения в √2 раз, т. е. I= (Im/√2) =0,707*Im.
Если синусоидальный ток i нагревает проводник, например, до температуры 100 °С, то постоянный ток, значение которого равно амплитуде синусоидального (Iп = Im), нагреет тот же проводник сильнее. Чтобы нагреть проводник постоянным током до тех же 100 °С, необходимо значение тока уменьшить до I=(Im/√2) =0,707*Im. Такое же значение будет справедливо и для U = Um/√2. В некоторых источниках действующие значения называют эффективными значениями.
Слайд 10Шкалы измерительных приборов переменного тока отградуированы в действующих значениях тока и
напряжения. Вольтметр, включенный в розетку промышленной сети, покажет напряжение 220 В. Это действующее значение синусоидального напряжения, амплитудное значение которого равно
Слайд 11 Таким образом, в ЭЦ переменного тока следует различать:
• мгновенные значения
ЭДС, напряжения, тока и мощности е, u, i, р;
• амплитудные значения Еm, Um, Im, Рm
• действующие значения Е, U, I, Р.
Основными параметрами синусоидальных колебаний принято считать:
амплитуду Аm;
частоту f или период Т = 1 /f;
начальную фазу φ
• амплитудные значения Еm, Um, Im, Рm
• действующие значения Е, U, I, Р.
Основными параметрами синусоидальных колебаний принято считать:
амплитуду Аm;
частоту f или период Т = 1 /f;
начальную фазу φ
Слайд 12 В линейных цепях синусоидальная ЭДС создает синусоидальный ток, как в ветви
с активным сопротивлением, так и в ветвях с емкостью и индуктивностью.
Однако в отличие от постоянного тока в ЭЦ переменного тока на отдельных участках напряжение и ток могут не совпадать по фазе, т. е. их начальные фазы φU и φI не равны. Следовательно, между ними появляется фазовый сдвиг φ = φU - φI.
Это объясняется наличием в ЭЦ конденсаторов и катушек индуктивностей с реактивным сопротивлением, обладающим свойством инерционности.
Однако в отличие от постоянного тока в ЭЦ переменного тока на отдельных участках напряжение и ток могут не совпадать по фазе, т. е. их начальные фазы φU и φI не равны. Следовательно, между ними появляется фазовый сдвиг φ = φU - φI.
Это объясняется наличием в ЭЦ конденсаторов и катушек индуктивностей с реактивным сопротивлением, обладающим свойством инерционности.
Слайд 13Векторные диаграммы
Поскольку синусоидальная функция определяется амплитудой и начальной фазой, то она
может быть изображена в виде вектора, длина которого пропорциональна амплитуде, а полярный угол — начальной фазе.
Введение векторов и векторных диаграмм значительно упрощает расчеты ЭЦ переменного тока. Например, если заданы токи в узле ЭЦ:
то в соответствии с первым законом Кирхгофа результирующий ток i = i1 + i2 +i3.
Введение векторов и векторных диаграмм значительно упрощает расчеты ЭЦ переменного тока. Например, если заданы токи в узле ЭЦ:
то в соответствии с первым законом Кирхгофа результирующий ток i = i1 + i2 +i3.
Слайд 14 Сложить мгновенные значения синусоидальных токов практически невозможно, поэтому прибегают к помощи
векторов. Складывая векторы, изображенные в определенном масштабе, по правилу параллелограмма или топографическим методом (из конца одного вектора откладывается начало другого и т.д.), определяют суммарный вектор тока, а значит, амплитудное значение тока Im и его начальную фазу φ.