- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Уравнение бегущей волны. Волны в среде
Содержание
- 1. Презентация к уроку Уравнение бегущей волны. Волны в среде
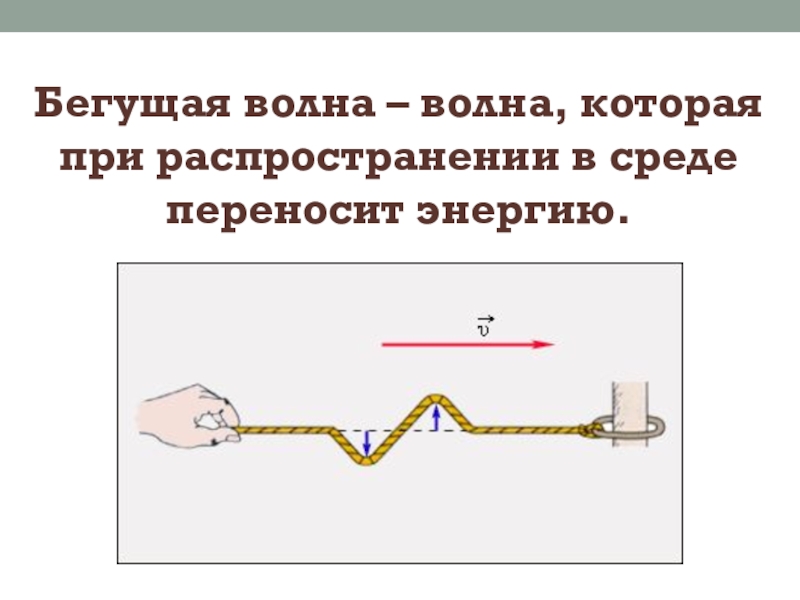
- 2. Бегущая волна – волна, которая при распространении в среде переносит энергию.
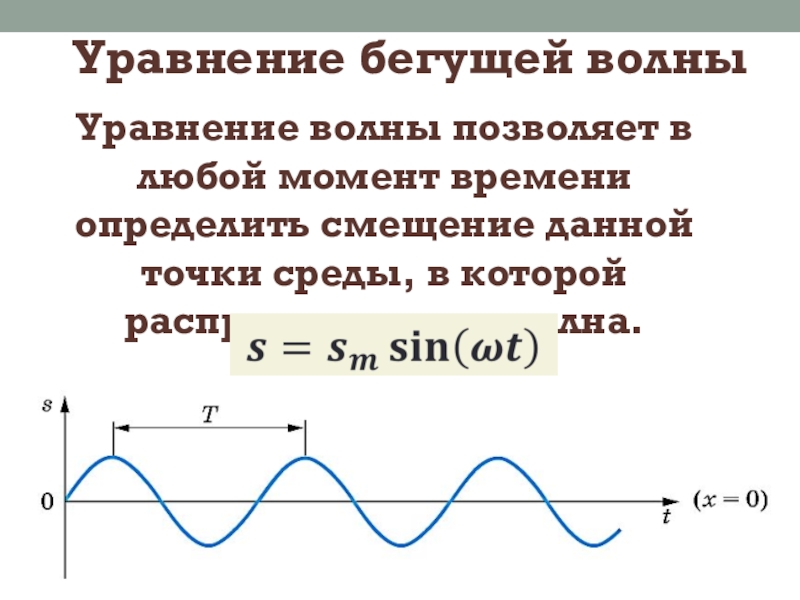
- 3. Уравнение бегущей волныУравнение волны позволяет в любой момент
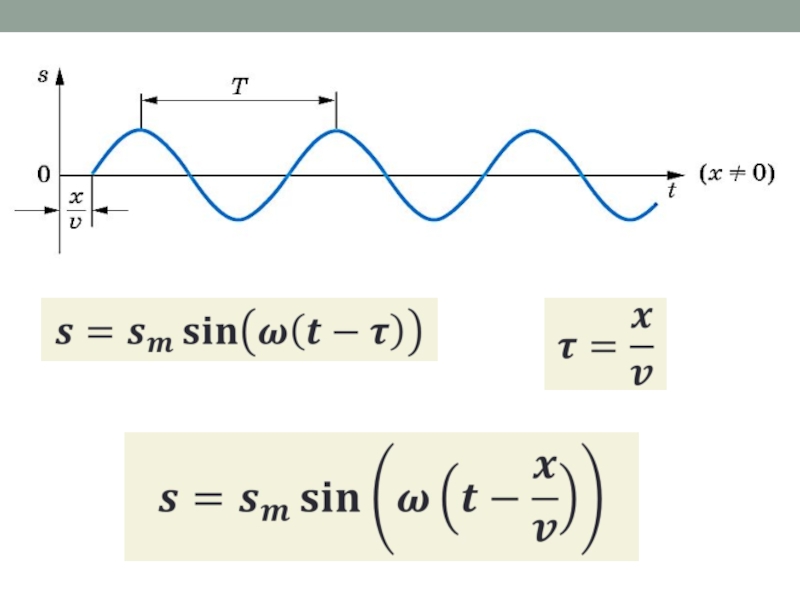
- 4. Слайд 4
- 5. Уравнение гармонической бегущей волны можно записать в
- 6. ВОЛНЫ В СРЕДЕ
- 7. Геометрическое место точек, в которых колебания происходят
- 8. Фронт волны — геометрическое место точек, до которых
- 9. Слайд 9
- 10. Плоская волна – это волна, волновые поверхности
- 11. Сферическая волна – это волна, волновые поверхности которой
- 12. Задача 1Определите скорость распространения υ поперечной волны
- 13. Задача 2Определить частоту звуковых колебаний в стали,
- 14. Задача 3Плоская поперечная волна задана уравнением
- 15. Задача 4Точки, находящиеся на одном луче и
- 16. Задача 5Уравнение волны имеет вид x=sin 2,5πt.
Бегущая волна – волна, которая при распространении в среде переносит энергию.
Слайд 3Уравнение бегущей волны
Уравнение волны позволяет в любой момент времени определить смещение данной
точки среды, в которой распространяется волна.
Слайд 5Уравнение гармонической бегущей волны можно записать в виде:
s = smsin (ωt – kx),
где k — волновое число
Фазы
колебаний двух точек, находящихся на расстоянии λ, отличаются на 2π, то есть колебания происходят в фазе.
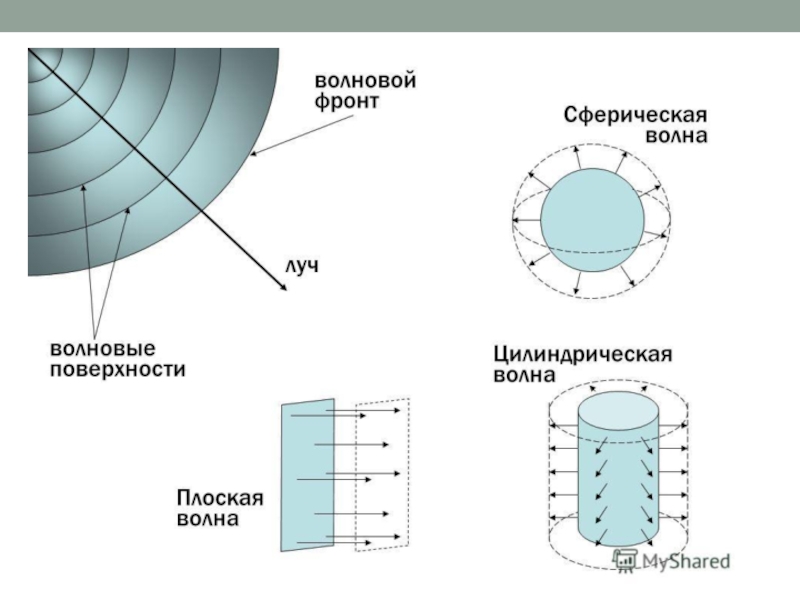
Слайд 7Геометрическое место точек, в которых колебания происходят в одной фазе, называется волновой
поверхностью.
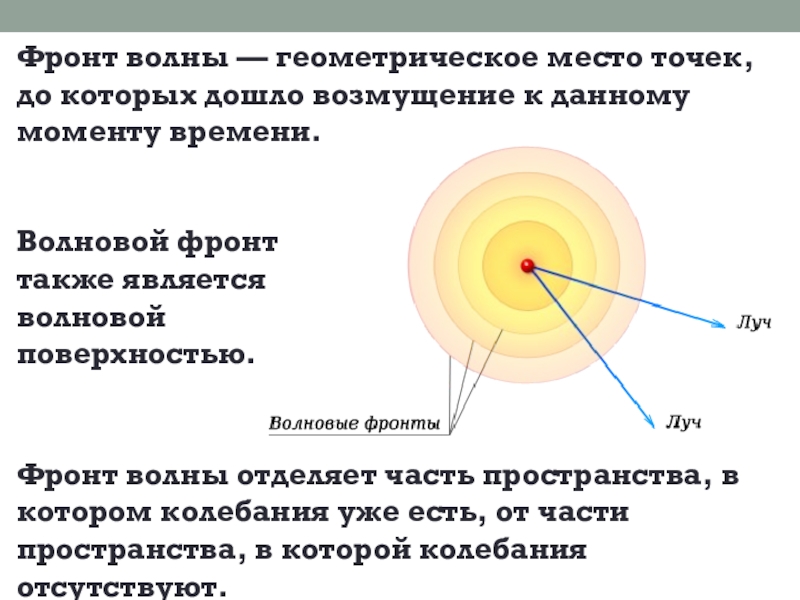
Луч — линия, перпендикулярная к волновой поверхности и к фронту волны. Направление луча указывает направление переноса энергии волной.
Слайд 8Фронт волны — геометрическое место точек, до которых дошло возмущение к данному
моменту времени.
Волновой фронт также является волновой поверхностью.
Фронт волны отделяет часть пространства, в котором колебания уже есть, от части пространства, в которой колебания отсутствуют.
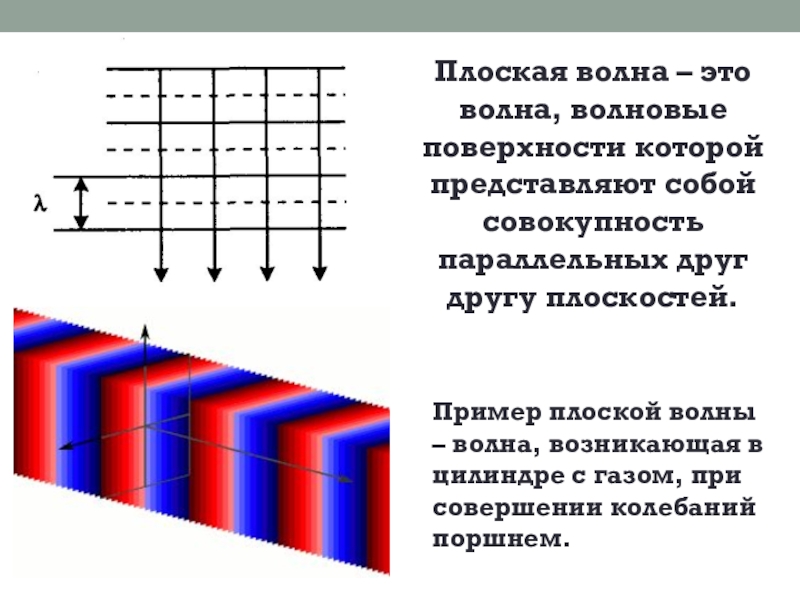
Слайд 10Плоская волна – это волна, волновые поверхности которой представляют собой совокупность
параллельных друг другу плоскостей.
Пример плоской волны – волна, возникающая в цилиндре с газом, при совершении колебаний поршнем.
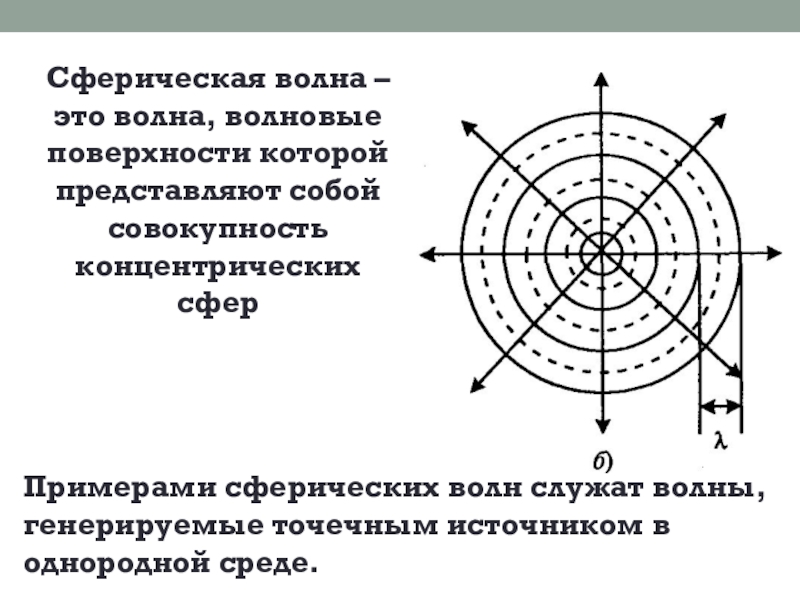
Слайд 11Сферическая волна – это волна, волновые поверхности которой представляют собой совокупность концентрических
сфер
Примерами сферических волн служат волны, генерируемые точечным источником в однородной среде.
Слайд 12Задача 1
Определите скорость распространения υ поперечной волны в струне, площадь поперечного
сечения которой S , если модуль силы ее натяжения F можно считать постоянным, а плотность вещества, из которого изготовлена струна равна ρ.
Слайд 13Задача 2
Определить частоту звуковых колебаний в стали, если расстояние между ближайшими
различающимися по фазе на Δφ= 90° точками звуковой волны ℓ = 1,54 м. Скорость звуковых волн в стали v = 5000 м/с.
Слайд 14Задача 3
Плоская поперечная волна задана уравнением
s = 2 • 10~4 sin
(628 t - 0,3х),
где s — смещение частицы в направлении, перпендикулярном направлению распространения волны, х — расстояние вдоль луча от источника колебаний. Определите частоту колебаний V, скорость распространения волны и, длину волны X и амплитуду колебаний скорости каждой частицы ит. Все величины в данном уравнении выражены в единицах СИ.
Слайд 15Задача 4
Точки, находящиеся на одном луче и удаленные от источника колебаний
на L1=12м и L2=14,7м, колеблются с разностью фаз 3п/2 рад. Определите скорость распространения колебаний в данной среде, если период колебания источника 1мс.
Слайд 16Задача 5
Уравнение волны имеет вид x=sin 2,5πt.
Найти смещение от положения
равновесия, скорость и ускорение точки, находящейся на расстоянии r = 20 м от источника колебаний, для момента времени t=1c после начала колебаний. Скорость распространения колебаний v=100 м/c
