- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад исследовательской работы на тему Математические цепочки
Содержание
- 1. Презентация исследовательской работы на тему Математические цепочки
- 2. Математические цепочки
- 3. Слайд 3
- 4. Слайд 4
- 5. Кто из нас не
- 6. Чтобы активно
- 7. Для меня особый интерес в
- 8. А существуют ли такие взаимосвязи в заданиях
- 9. Слайд 9
- 10. Слайд 10
- 11. Предмет исследования: математика.Объект исследования: математические цепочки. Гипотеза:
- 12. Взаимообратные связи
- 13. Умножение вводится как действие, заменяющее особый случай
- 14. Используя эти теоретические знания, знание переместительного
- 15. Математические цепочки А
- 16. Рассмотрим математические цепочки, в которых можно последовательно
- 17. Ведь все операции, которые мы последовательно выполнили
- 18. Проверим, что наше утверждение верно на других
- 19. Вывод: предположение: если от данного числа а
- 20. Сбор собственного материала,
- 21. Можно и усложнить задание в цепочке:
- 22. 3) Теперь, на мой
- 23. Если же ведущий игру, выполнит
- 24. Теперь, зная ключ к выполнению таких заданий,
- 25. 4) В заданиях
- 26. 5) В жизни бывают такие ситуации, решение
- 27. Мама испекла пирожки и отдала
- 28. Примем за 1 часть те
- 29. Собственные выводы:1) Взаимообратные
- 30. Библиография:1) Исследовательская
- 31. Спасибо за внимание!
Слайд 1
«Мой первый доклад»
Математические цепочки
Автор: Пьянзина Юлия Александровна,
МБОУ Тазовская средняя общеобразовательная школа
Руководитель: Фильцова Раиса Алексеевна,
учитель начальных классов
П. Тазовский, ЯНАО, 2011 год
Слайд 3
Чтоб врачом, моряком или летчиком стать,
Надо, прежде всего, математику знать.
Математику уже затем учить следует,
Что она ум в порядок приводит.
М.В. Ломоносов
Слайд 5
Кто из нас не мечтает стать моряком, летчиком,
Математика, как и другие науки, непрерывно развивается, обогащается новыми теориями, перестраивается в ответ на новые запросы жизни.
Часто говорят, что математика скучна. Так думают те, кто дальше ее начатков не ушел. Математика пленяет всех тех, кто достаточно продвигается в ее изучении. Недаром выдающаяся русская женщина – математик Софья Васильевна Ковалевская писала:
«Нельзя быть математиком, не будучи в то же время поэтом в душе».
Слайд 6
Чтобы активно участвовать в большой интересной
Вычислительная деятельность
позволяет развивать:
мышление;
учебно-познавательные мотивы;
опыт творческой деятельности;
приобретать действенные знания и умения.
Слайд 7 Для меня особый интерес в математике
Эти знания позволяют активно включаться в учебную деятельность и отрабатывать вычислительные навыки, а также самостоятельно составлять и решать тройки-четверки примеров, связанных между собой обратной связью, задачи, обратные данным, творческие задания игрового характера, и тем самым расширять содержание своего математического образования.
Слайд 8
А существуют ли такие взаимосвязи в заданиях более сложного характера, где
Можно ли эти знания применять в решении задач, отражающих некоторые жизненные ситуации?
Желание найти ответы на эти вопросы стало основой для моей работы и определило ее цель.
Слайд 9 Цель:
выявить наличие взаимообратной
Слайд 10 Задачи:
изучить теорию взаимосвязи
произвести сбор учебного практического материала – математических цепочек и выполнить в них преобразования в используя знания взаимосвязи арифметических действий;
3)проанализировать полученные результаты и выявить наличие взаимосвязи;
4) найти способы применения полученных знаний при выполнении других математических заданий
Слайд 11Предмет исследования: математика.
Объект исследования: математические цепочки.
Гипотеза: если от данного
Слайд 12
Взаимообратные связи
С первого знакомства вычитание рассматривается как операция обратная сложению:
а + в = с с – а = в с – в = а,
а деление как операция обратная умножению:
а х в = с с : а = в с : в = а,
Если сложение мы рассматриваем как объединение частей в целое множество, то вычитание – удаление части исходного множества.
Слайд 13
Умножение вводится как действие, заменяющее особый случай сложения – сложение одинаковых
3 + 3 + 3 + 3 = 3 х 4 а + а + а + а = а х к, где к – количество слагаемых
3 х 4 = 12 а х к = в
При первом знакомстве с делением мы рассматриваем ситуацию, приводящую к этому действию, в которой решение проблемы (учебной задачи) связывает деление не столько с умножением, сколько с вычитанием несколько раз одного и того же числа из целого:
12 – 3 – 3 – 3 – 3, в 12 по 3 содержится 4 раза 12 : 3 = 4 в : а = к
Слайд 14
Используя эти теоретические знания, знание переместительного закона относительно сложения и
48 +22 = 70 а + в = с 8 х 7 =56 а х в = с
22 + 48 = 70 в + а = с 7 х 8 = 56 в х а = с
70 - 48 = 22 с – а = в 56 : 8 = 7 с : в = а
70 - 22 = 48 с – в = а 56 : 7 = 8 с : а = в
тем самым расширять содержание своего образования и отрабатывать вычислительные навыки, то есть учиться хорошо и быстро считать, а также применять эти знания в сложных математических выражениях, решая их прямым и обратным путем; составлять творческие задания игрового характера.
Слайд 15 Математические цепочки
А существуют ли такие взаимосвязи
Слайд 16
Рассмотрим математические цепочки, в которых можно последовательно выполнять различные математические операции
36 + 14 = * * - 27 = ** ** + 18 = 41
36 + 14 = 50 50 - 27 = 23 23 + 18 = 41
Выполняя последовательно операции, мы осуществляем преобразование данного числа 36 в новое число прямым путем, получим число 41 .
А можно ли выполнить преобразование в обратном порядке и от числа 41 вернуться к числу 36 ?
Слайд 17
Ведь все операции, которые мы последовательно выполнили с каждым результатом предыдущего
Проверим это, выполняя операции, обратные данным, выполняя преобразование с конца:
41 - 18 = 23 23 + 27 = 50 50 - 14 = 36
Получили первоначальное число 36 .
Значит, такое преобразование возможно.
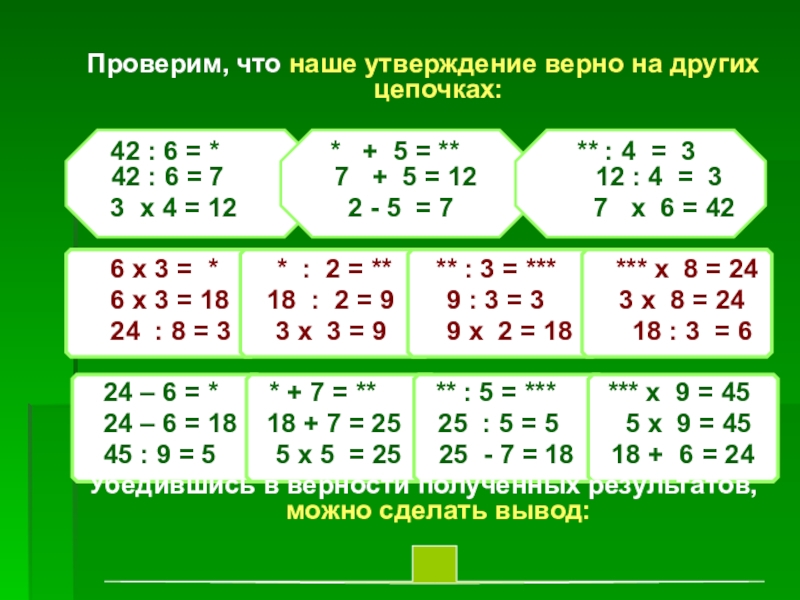
Слайд 18Проверим, что наше утверждение верно на других цепочках:
42 :
3 х 4 = 12 2 - 5 = 7 7 х 6 = 42
6 х 3 = * * : 2 = ** ** : 3 = *** *** х 8 = 24
6 х 3 = 18 18 : 2 = 9 9 : 3 = 3 3 х 8 = 24
24 : 8 = 3 3 х 3 = 9 9 х 2 = 18 18 : 3 = 6
24 – 6 = * * + 7 = ** ** : 5 = *** *** х 9 = 45
24 – 6 = 18 18 + 7 = 25 25 : 5 = 5 5 х 9 = 45
45 : 9 = 5 5 х 5 = 25 25 - 7 = 18 18 + 6 = 24
Убедившись в верности полученных результатов, можно сделать вывод:
Слайд 19
Вывод: предположение: если от данного числа а последовательно выполнить несколько арифметических
оказалось верным, и его можно представить в общем виде:
если:
а – к = * * + с = ** ** : у = *** *** х р = в,
то
в : р = *** *** х у = ** ** - с = * * + к = а
Слайд 20 Сбор собственного материала, его анализ и
1) Знания взаимосвязи арифметических действий теперь можно использовать, составляя самостоятельно и решая сколько угодно новых математических цепочек:
9 х 6 = О О + 18 = О О : 9 = О О х 7 = О О – 49 = 7
7 + 49 = 56 56 : 7 = 8 8 х 9 = 72 72 – 18 = 54 54 : 6 = 9
100 – 64 = О О х 2 = О О : 8 = О О + 46 = О О х 4 = 220
220 : 4 = 55 55 – 46 = 9 9 х 8 = 72 72 : 2 = 36 36 + 64 = 100
Слайд 21Можно и усложнить задание в цепочке: число, с
которого начинаются
неизвестным (а конечный результат известным) и
найти его, выполняя с конца операции обратные
данным:
О : 9 = О О + 91 = О О : 4 = О
О - 7 = О О х 6 = 108
108 : 6 = 18 18 + 7 = 25 25 х 4 = 100
100 – 91 = 9 9 х 9 = 81
Проверка:
81 : 9 = 9 9 + 91 = 100 100 : 4 = 25
25 - 7 = 18 1 8 х 6 = 108
Слайд 22
3) Теперь, на мой взгляд, легко найти ключ,
Например: Я задумала число, увеличила его в 5 раз, полученный результат уменьшила на 2, новый результат уменьшила в 3 раза, и у меня получилось число 6.
(а х 5 - 2) : 3 = 6 , выполняя последовательно от полученного числа операции, обратные данным с конца, получим:
(6 х 3 + 2) : 5 = 4 проверим правильность
решения:
(4 х 5 - 2) : 3 = 6 (верно)
значит: если :
а х в - с) : р = у, то (у х р + с) : в = а
Слайд 23
Если же ведущий игру, выполнит (незаметно для игроков) обратные
а х 8 : 2 х 5 : а = 20: 8 : 2 х 5 = 20,
значит
задуманное число должно было увеличиться в 20 раз, но так как полученный результат разделили на задуманное число, то число 20 – общий результат всех преобразований - получилось в ответе:
(20)
а х 8 : 2 х 5 : а = 20
Слайд 24
Теперь, зная ключ к выполнению таких заданий, можно их разнообразить и
Мы с Катей задумали разные числа, выполнили действия и получили одинаковый результат.
а х 3 = * * + 43 = ** ** – 10 = *** в : 5 = * * - 4 = ** ** + 54 = ***
Я задумала наибольшее однозначное число. Какое число задумала Катя?
Выполняя преобразования в прямом и обратном порядке, получаем:
9 х 3 = 27 27 + 43 = 70 70 – 10 = 60
60 - 54 = 6 6 + 4 =10 10 х 5 = 50
Катя задумала число – 50.
Слайд 25
4) В заданиях на смекалку
О + 14 - 25 = 69
О = 69 + 25 -14 О = 80
3 х О : 2 х 7 = 42
О = 42 : 7 х 2 : 3 О = 4
О : 4 х 3 х 5 : 6 = 20
О = 20 х 6 : 5 : 3 х 4 О = 32
Слайд 26
5) В жизни бывают такие ситуации, решение которых влечет тоже цепочку
Рассмотрим такие задачи:
Праздничный пирог разрезали на две равные части. Одну половину оставили, а другую разрезали еще на равных 8 частей.
Какова масса всего пирога, если масса
одного куска пирога равна 100 граммам?
Рассуждение ведем с конца: если масса одного куска пирога 100 граммов, а это 1/8 часть половины пирога, то можно узнать половину пирога: 100 х 8 = 800 (г), так как половина пирога составляет 800 граммов, то масса всего пирога в два раза больше:
800 х 2 = 1600 (г), то есть:
100 х 8 х 2 = 1600 (г) – масса пирога.
Слайд 27 Мама испекла пирожки и отдала Красной Шапочке половину пирожков
Слайд 28
Примем за 1 часть те пирожки, которые Красная Шапочка
1 – 1/3 =2/3 (ч.) принесла Бабушке
6 : 2 х 3 = 9 (п.) пирожки Бабушки и Волка
9 + 1 = 10 (п.) половина всех пирожков
10 х 2 = 20 (п.) испекла мама
Слайд 29
Собственные выводы:
1) Взаимообратные связи действий сложения и
2) Эти знания можно применять не только в решении примеров, связанных между собой обратной связью, задач, обратных данным, но и в составлении и решении игровых заданий, задач на смекалку, задач, отражающих некоторые жизненные ситуации и, тем самым, расширять содержание своего математического образования.
3) Предметные теоретические знания, которые мы учимся добывать в школе, надо учиться применять на практике. Тогда пробуждается интерес к предмету, желание и стремление открывать новое, и мы активно включаемся в учебную деятельность, приобретаем действенные знания, умения и навыки, опыт самостоятельной и творческой деятельности.
Слайд 30 Библиография:
1) Исследовательская работа школьников. Научно-методический информационно-публицистический
2) В.П. Труднев. Внеклассная работа по математике в начальной школе. М., «Просвещение», 1975..
3) Начальная школа. Научно-методический журнал. М., «Начальная школа и образование», № 1, 2008.
4) Начальная школа. Научно-методический журнал. М., «Начальная школа и образование», № 4, 2009
5) И.И. Аргинская. «Математика», 1, 2, 3 классы, Самара: Корпорация «Федоров», издательство «Учебная литература», 2007.
6) М.И. Моро, М.А. Бантова и др. «Математика 3», учебник для начальной школы в 2 частях, М., «Просвещение», 2009.