Обобщение опыта учителя начальных классов
МБОУ лицея № 14
Кулешовой Марины
Васильевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Обобщение опыта на тему Методы анализа и синтеза в решении задач на уроках математики в рамках ФГОС.
Содержание
- 1. Обобщение опыта на тему Методы анализа и синтеза в решении задач на уроках математики в рамках ФГОС.
- 2. СОДЕРЖАНИЕ:1. Информационный раздел.2.Теоретическая база опыта.3. Методологическая база опыта.4. Результативность опыта.5. Рефлексия.6. Библиографический список.
- 3. 1. Информационный раздел Актуальность
- 4. 1. Информационный разделРешение задач способствует разви-тию младших
- 5. Используя в начальном обучении математике приёмы анализаи
- 6. Анализ. Логический прием или метод исследования,
- 7. При решении задач анализ может выступать в
- 8. 2. Теоретическая база опыта Теоретической основой
- 9. концепция личностно-ориен- тированного обучения (Д.А.Белухин, И.С.Якиманская);положения
- 10. 3. Методологическая база опыта
- 11. 3. Методологическая база опытапринципы взаимосвязи теории и практики;фундаментальные основы развития образования.
- 12. Ведущая педагогическая идея
- 13. 4. Результативность опыта Для того, чтобы научить
- 14. Слайд 14
- 15. Анализ условияПрочтение текста (неоднократно).Осмысление текста (сюжет, числовые данные).Моделирование (модель помогает решению задачи).
- 16. Простая
- 17. МоделированиеКраткая записьБыло – 15 гр.Съел – 8
- 18. Составная
- 19. Какие числовые данные ещё есть в
- 20. МоделированиеКраткая записьI – 25 стр.II – ?,
- 21. ПОИСК РЕШЕНИЯВоспроизведение определений, описывающих ту область явлений, о которой говорится в задаче.Составление плана решения задачи.
- 22. Найденное решение излагают синтетическим методом, а чтобы
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Анализ составной задачиМожем найти? (Да.)Каким
- 27. Слайд 27
- 28. Слайд 28
- 29. Основные средства учителя,
- 30. 5. Рефлексия Приёмы анализа и синтеза
- 31. Слайд 31
- 32. 6. Библиографический списокА. В. Тихвинская, Л.Ф. Батан,
Слайд 1 Методы анализа и синтеза в решении задач на уроках математики в
Слайд 2СОДЕРЖАНИЕ:
1. Информационный раздел.
2.Теоретическая база опыта.
3. Методологическая база опыта.
4. Результативность опыта.
5. Рефлексия.
6.
Слайд 31. Информационный раздел
Актуальность опыта заключается в том,
Математика даёт реальные предпосылки для развития мышления. Математическая задача помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни.
Слайд 41. Информационный раздел
Решение задач способствует разви-
тию младших школьников.
Как обучать детей
способа решения текстовой
задачи, с которой они встречаются
с первых дней занятий в школе?
Этот вопрос – центральный в
методике обучения решению задач.
Слайд 5Используя в начальном обучении
математике приёмы анализа
и синтеза, учитель содействует ак-
тивизации
и тем самым способствует развитию его основных мыслительных
операций:анализа,синтеза, сравнения, обобщения, аналогии.
1. Информационный раздел
Слайд 6
Анализ. Логический прием или
метод исследования, состоящий
в
Понятия анализ и синтез были известны еще в Древней Греции. В переводе с древнегреческого анализ означает "решение", "разрешение".
Слайд 7При решении задач анализ может выступать в двух формах:
а) когда
б) когда целое расчленяют на части.
Соответственно, синтез – это рассуждение:
а) когда двигаются от данных задачи к искомым;
б) когда элементы объединяют в целое.
Слайд 82. Теоретическая база опыта
Теоретической основой опыта служат :
идеи личностного
и акмеологического (Б.Г.Ананьев, Н.В.Кузьмина,А.Г.Ситников)
подходов обучения;
положения новой образовательной парадигмы (В.В. Краевский, В.П.Казначеев);
Слайд 9концепция личностно-ориен-
тированного обучения (Д.А.Белухин, И.С.Якиманская);
положения о творческом характере педагогической
2. Теоретическая база опыта
Слайд 103. Методологическая база опыта
Методологической основой опыта
материалистическая аксиология, в рамках которой человек рассматривается как высшая ценность и самоцель общественного развития;
положения о социальной, деятельностной и творческой сущности личности и её многофакторном характере развития;
Слайд 113. Методологическая база
опыта
принципы взаимосвязи теории
и практики;
фундаментальные основы
Слайд 12Ведущая педагогическая идея
этого педагогического опыта
необходимости организации
учебной деятельности с
учетом развития каждого
ученика, продуктивного
мышления, стратегии использования
и совершенствования его
мыслительных операций.
Слайд 134. Результативность опыта
Для того, чтобы научить
учеников решать задачи,
необходимо
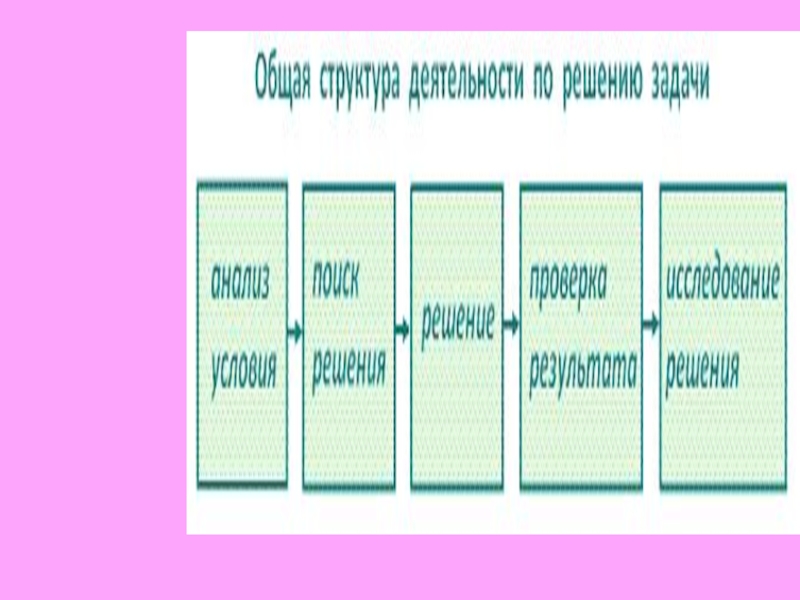
структура мыслитель-
ной деятельности ученика
по решению задачи.
Слайд 15Анализ условия
Прочтение текста (неоднократно).
Осмысление текста (сюжет, числовые данные).
Моделирование
(модель помогает решению
Слайд 16 Простая задача. В вазе было
О чём говорится в задаче? (О грушах.)
Сколько было груш? (15)
Какие числовые данные ещё есть в задаче? (Утром Ваня съел 8 груш.) Съел – что сделал? (Уменьшил.)
Что нужно найти? (Сколько груш осталось.)
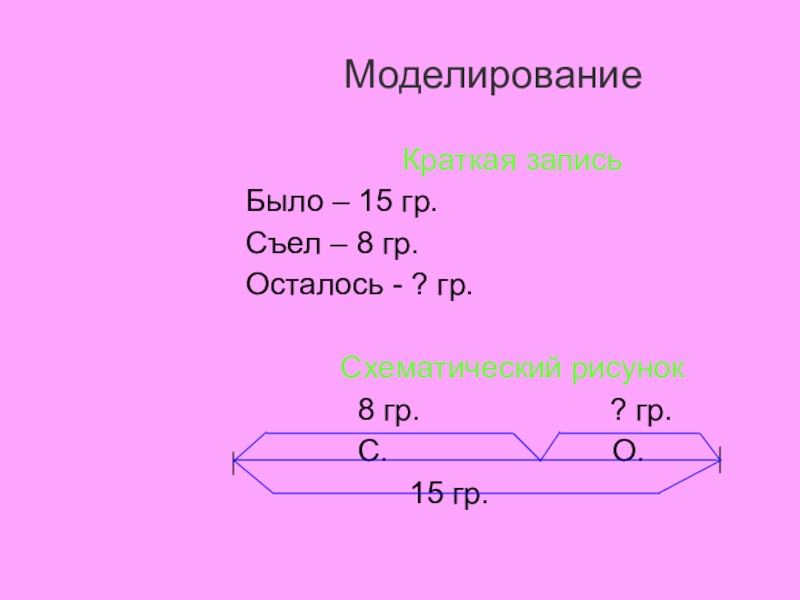
Слайд 17Моделирование
Краткая запись
Было – 15 гр.
Съел – 8 гр.
Осталось - ? гр.
Схематический
8 гр. ? гр.
С. О.
15 гр.
Слайд 18 Составная задача. В книге было 97
О чём говорится в задаче? (О страницах книги.) Что о них говорится? (Их прочитали.)
Что известно в задаче? (В книге было 97 страниц.)
Слайд 19Какие числовые данные ещё
есть в задаче?
(В 1-й день
25 страниц, а во 2-й на 15
страниц больше.) Что значит на
15 больше? (Это значит
столько же да ещё 15.)
Что нужно найти? (Сколько
страниц прочитал школьник
в 3-й день.)
Составная задача.
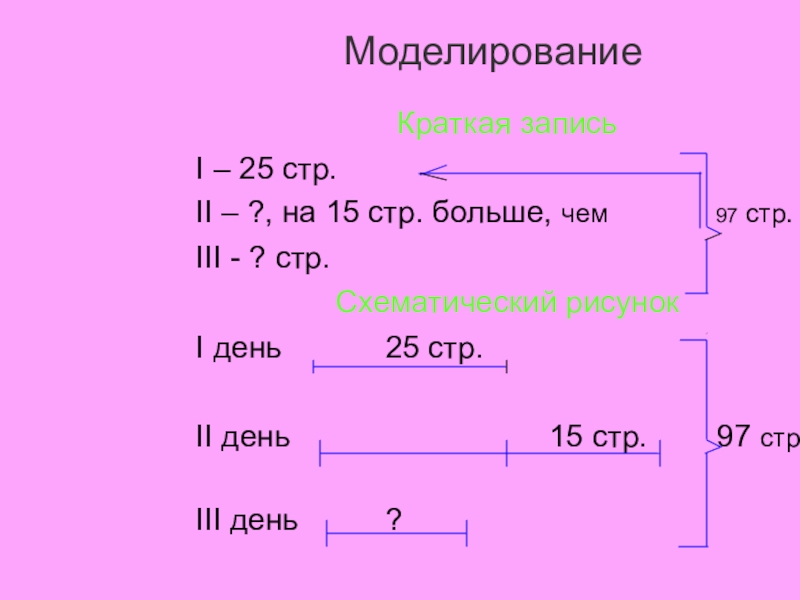
Слайд 20Моделирование
Краткая запись
I – 25 стр.
II – ?, на 15 стр. больше,
III - ? стр.
Схематический рисунок
I день 25 стр.
II день 15 стр. 97 стр.
III день ?
Слайд 21ПОИСК РЕШЕНИЯ
Воспроизведение определений, описывающих ту область явлений, о которой говорится в
Составление плана решения задачи.
Слайд 22Найденное решение излагают синтетическим методом, а
чтобы найти способ решения, пользуются
При решении синтезом в сознании проводится и анализ, но достаточно быстро и подсознательно.
ПОИСК РЕШЕНИЯ
Слайд 26 Анализ составной задачи
Можем найти? (Да.)
Каким действием?
(Сложением, на что
слово «больше»)
Проговорите это действие.
25+15=40 (стр.)
Слайд 29 Основные средства
учителя, позволяющие
научить решать задачи,
используя приёмы
анализа и синтеза:
1) Образец решения задачи (особенно на первом этапе).
2) Алгоритмическое предписание.
3) Обучение эвристическим методам решения задач на большом числе примеров.
4) Самостоятельное и заинте-
ресованное решение учащимися задач, способ решения которых им не известен, но материал которых не выходит за рамки их знаний.
Слайд 305. Рефлексия
Приёмы анализа и синтеза при решении задач на
На мой взгляд, необходимо
вооружить детей основными способами, которые позволят им самостоятельно решать задачи не
только в учебнике, но и задачи, возникающие в реальной жизни.
Слайд 326. Библиографический список
А. В. Тихвинская, Л.Ф. Батан, М.Н. Сухоносенко - «Обучение
В.Ф. Шаталов «Точка опоры»-М:Педагогика,1987
Г.В.Дорофеев Дифференциация в обучении математике.// Математика в школе.-1990.№6.-С.15-20.
Зайцева С.А. Решение составных задач на уроках математики / С.А. Зайцева , И.И.Целищева – Москва: Чистые пруды, 2006
З.И.Калмыкова Психологические принципы развивающего обучения
Истомина Н.Б. Методика преподавания математики в начальных классах. – Москва, 2002
Педагогика: педагогические теории, системы, технологии: Учебное пособие для студентов сред. спец. пед. заведений / С.А. Смирнов, И.Б. Котова, Е.Н. Шиянов, Т.И. Баева и др. – Москва, 1998
Р.А. Утеева Формы учебной деятельности учащихся на уроке.// Математика в школе.-1995, №2.-с.33-34.
Сластёнин В.А., Исаев И.Ф., Мищенко А.И., Шиянов Е.Н. Педагогика: Учебное пособие для студентов пед. уч. заведений. – М.: Школа –Пресс, 1997