с реальными предметами действиями с уменьшенными образцами, моделями, с их графическими заменителями: рисунками, схемами, чертежами, таблицами.
Понять содержание задачи, выявить отношения между данными и искомым,
найти разные способы решения задачи,
увидеть новые, не отражённые в задаче отношения.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Моделирование текстовых задач
Содержание
- 1. Моделирование текстовых задач
- 2. Особенность методики моделирования задач: Методика обучения решению
- 3. Первый блок связан с осуществлением процесса моделирования
- 4. Второй блок связан с применением моделирования к
- 5. Третий блок связан с решением задач различными
- 6. В практике современной начальной школы идея моделирования
- 7. Согласно стандартам нового поколения, выпускник начальной школы
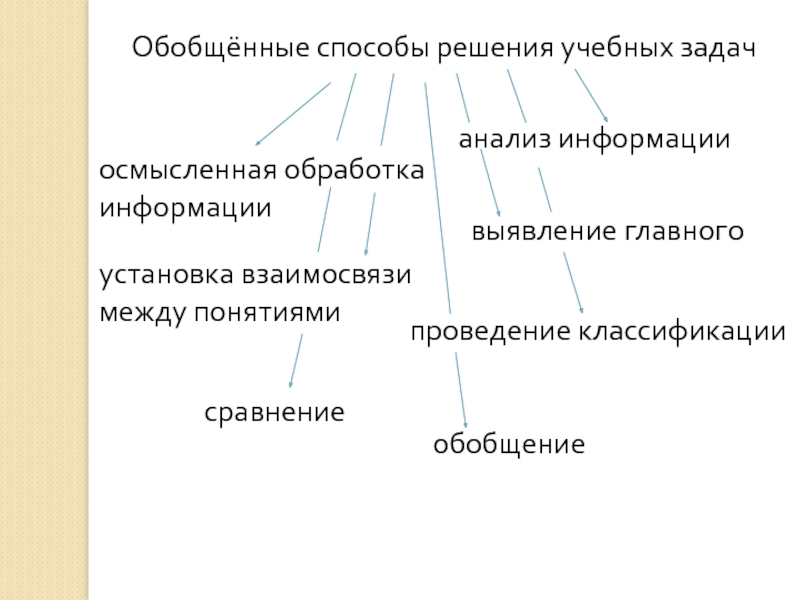
- 8. Обобщённые способы решения учебных задачосмысленная обработка информациианализ информациивыявление главногоустановка взаимосвязи между понятиямипроведение классификациисравнение обобщение
- 9. Применяя данный метод в своей работе, я
- 10. Моделирование задач позволяет младшим школьникам подняться на
- 11. «Моделирование – процесс построения моделей для каких-либо
- 12. Другими словами, изображение условия задачи при помощи
- 13. Прежде чем начинать работу по моделированию задач,
- 14. «КЛЮЧЕВЫЕ» СЛОВА В ТЕКСТЕ ЗАДАЧИ Разностное отношение
- 15. применяю метод моделирования при изучении математических понятий;веду
- 16. I ЭТАПВОСПРИЯТИЕ И АНАЛИЗ ЗАДАЧИЦель этапа: понять задачу, представить, о чём эта задача;
- 17. I I этап - МОДЕЛИРОВАНИЕЦель: установить,
- 18. Для формирования умения моделировать задачу, я использую
- 19. На мой взгляд, самой удачной, с этой
- 20. Начинаю работу по моделированию задач с первого
- 21. Графические модели решения задач по математике Задача
- 22. Первый подэтап: 1) Чтение текста задачи: сначала
- 23. Второй подэтап (графическая работа с цветом): Разбиение
- 24. Выбери схему, подходящую к данной задаче.
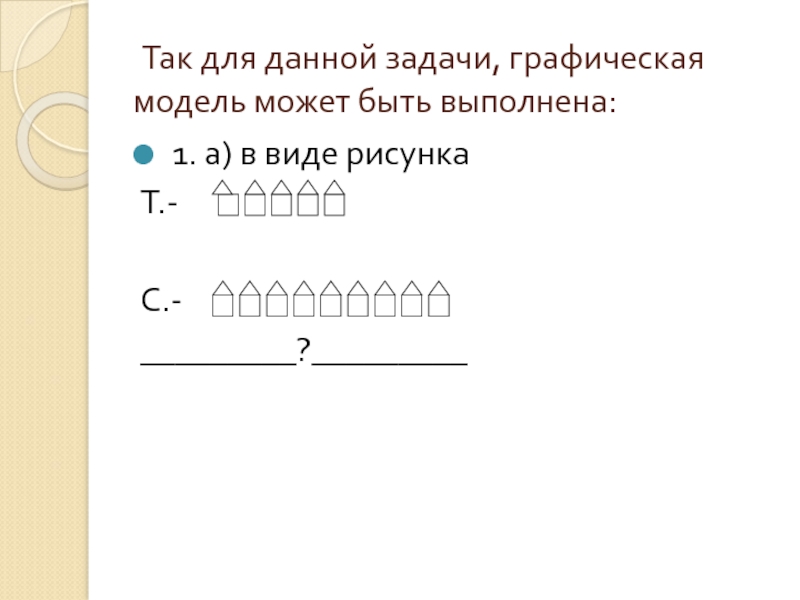
- 25. Так для данной задачи, графическая модель может быть выполнена: 1. а) в виде рисункаТ.- С.-_________?_________
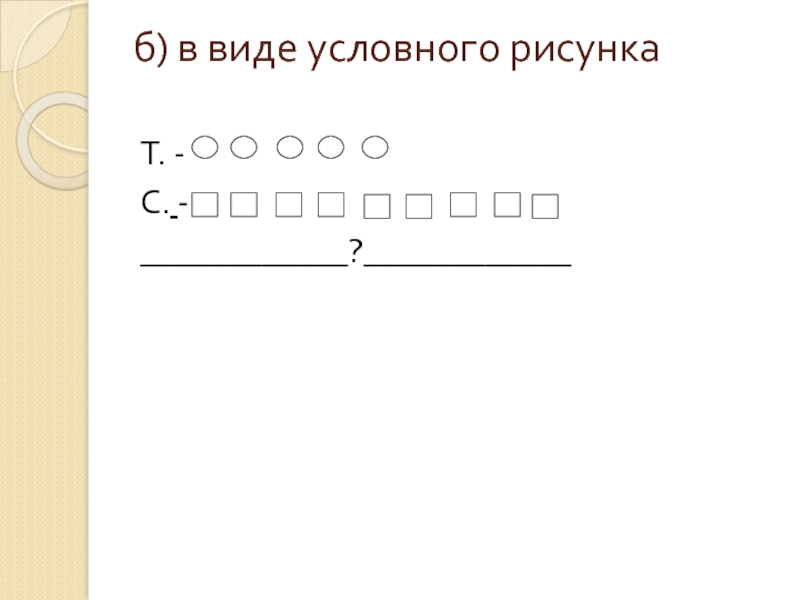
- 26. б) в виде условного рисунка Т. - С. - ____________?____________
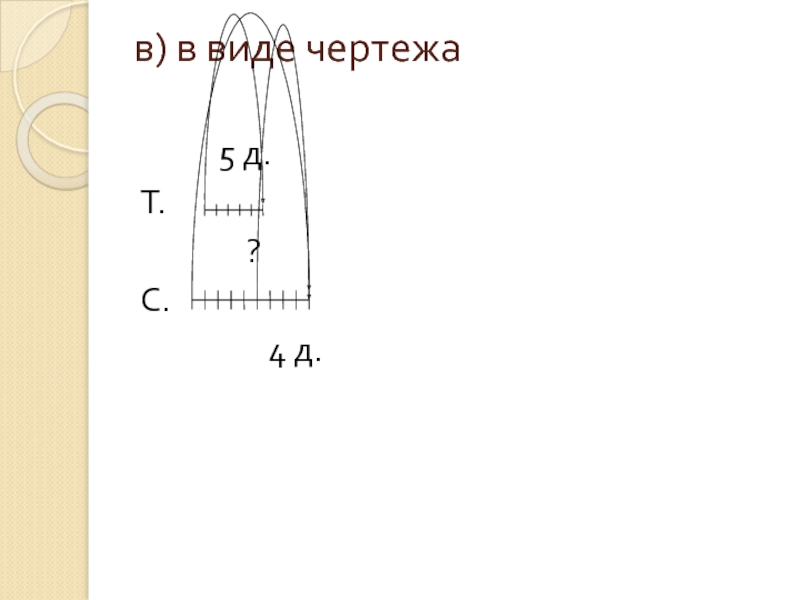
- 27. в) в виде чертежа
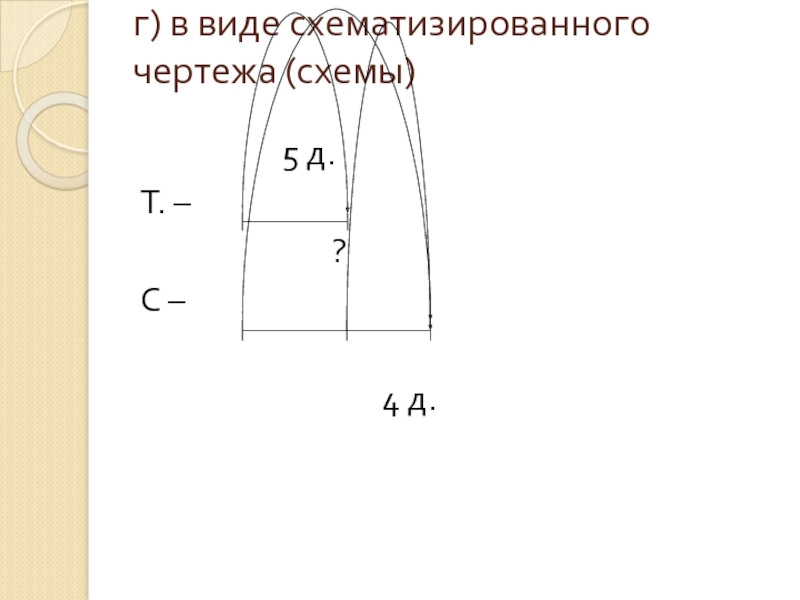
- 28. г) в виде схематизированного чертежа (схемы)
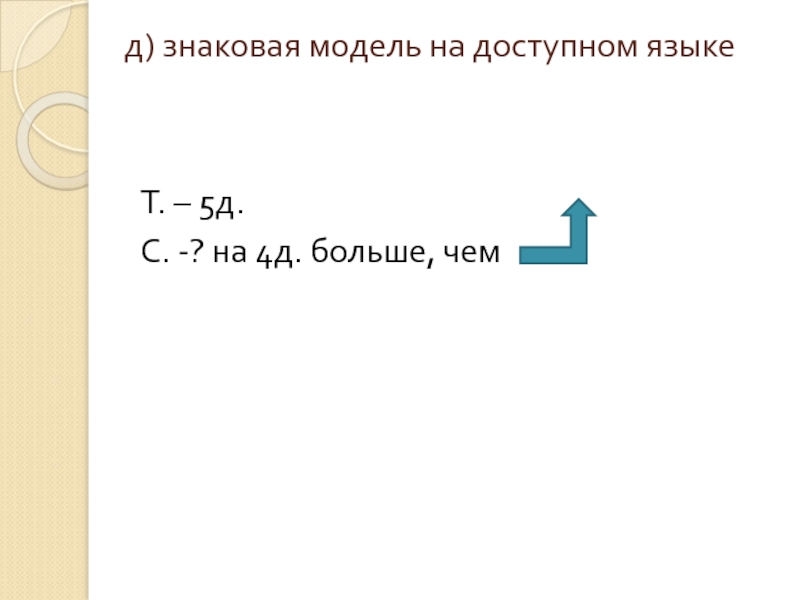
- 29. д) знаковая модель на доступном языке Т. – 5д.С. -? на 4д. больше, чем
- 30. е) знаковая модель выполненная на математическом языке5+4
- 31. Вывод:Каждая модель выступает как одна из форм
- 32. При анализе данной задачи детям предлагается сразу
- 33. Анализируя какие виды моделирования труднее всего для
- 34. Итогом своей работы считаю ВПР в 4
- 35. ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА:1. Истомина Н. Б. Методика обучения
Особенность методики моделирования задач: Методика обучения решению задач на основе моделирования реализована в системе учебных заданий, нацеленных на формирование трех блоков умений.
Слайд 1Моделирование текстовых задач
Цель: Формирование навыков моделирования текстовых задач.
Задачи:
научить заменять действия
Слайд 2Особенность методики моделирования задач: Методика обучения решению задач на основе моделирования
реализована в системе учебных заданий, нацеленных на формирование трех блоков умений.
Слайд 3Первый блок связан с осуществлением процесса моделирования и включает в себя
комплекс умений:
- моделировать ситуации с помощью различных видов моделей (предметных рисунков, условных рисунков);
- моделировать ситуации по-разному, создавая различные конструкции модели; ( неизменными должны оставаться основные величины и связи между ними; изменяться может порядок размещения величин, объектов, положение в пространстве );
- оперировать отрезками как простейшими графическими моделями;
- моделировать ситуацию путем построения схемы;
- моделировать ситуацию путем построения схем различной конструкции;
- моделировать условие задачи с помощью схемы;
- преобразовывать схему.
Слайд 4Второй блок связан с применением моделирования к решению текстовых задач и
включает в себя умения:
- устанавливать связь между схемой и математической записью;
- анализировать схему с целью получения необходимой (например, для решения задачи) информации;
- решать задачу на основе схематического моделирования.
Слайд 5Третий блок связан с решением задач различными способами на основе моделирования
и включает в себя умения:
- «открывать» новую информацию о задаче с помощью схематической модели;
- осуществлять процесс решения различными способами в целом;
- оценивать различные способы решения с точки зрения их рациональности.
Слайд 6В практике современной начальной школы идея моделирования реализована в ряде учебников
по математике (И. И. Аргинская, Э. И. Александрова, Н.Б. Истомина, Г.Г. Микулина, Л. Г. Петерсон).
А. В. Белошистая рассматривает моделирование в качестве основного способа деятельности при изучении младшими школьниками геометрических понятий, В. В. Малыхина предлагает использовать моделирование как один из приемов работы с задачей, и С. Е. Царева, где моделированию отводится роль приема поиска плана решения задачи и ее проверки.
А. В. Белошистая рассматривает моделирование в качестве основного способа деятельности при изучении младшими школьниками геометрических понятий, В. В. Малыхина предлагает использовать моделирование как один из приемов работы с задачей, и С. Е. Царева, где моделированию отводится роль приема поиска плана решения задачи и ее проверки.
Слайд 7Согласно стандартам нового поколения, выпускник начальной школы должен владеть обобщёнными способами
решения учебных задач, его необходимо научить
Это мыслительные операции, которые включают в себя словесно – логическое мышление. Этот тип мышления должен стать доминирующим к концу начальной школы
Это мыслительные операции, которые включают в себя словесно – логическое мышление. Этот тип мышления должен стать доминирующим к концу начальной школы
Слайд 8Обобщённые способы решения учебных задач
осмысленная обработка информации
анализ информации
выявление главного
установка взаимосвязи
между
понятиями
проведение классификации
сравнение
обобщение
Слайд 9Применяя данный метод в своей работе, я решаю такие важные задачи:
формировать умения
решать текстовые задачи;
доступный для обучающихся, уровень усвоения учебного материала при меньшей затрате времени и с большей эффективностью;
организация поисковой деятельности;
создание условий для обучения всех
доступный для обучающихся, уровень усвоения учебного материала при меньшей затрате времени и с большей эффективностью;
организация поисковой деятельности;
создание условий для обучения всех
Слайд 10Моделирование задач позволяет младшим школьникам подняться на достаточно высокую ступеньку абстрактности:
все второстепенные детали опущены, выбор действия производится только из логики происходящих изменений.
Слайд 11«Моделирование – процесс построения моделей для каких-либо познавательных целей. Модель –
это объект или система, исследование которой служит средством для получения знаний о другом объекте – оригинале или прототипе модели». (Л. М. Фридман, К. Н. Волков).
Слайд 12Другими словами, изображение условия задачи при помощи символов и знаков, позволяющих
выделить логические связи и установить закономерности.
Слайд 13Прежде чем начинать работу по моделированию задач, провожу подготовительную работу. Она
заключается в выполнении различных упражнений, позволяющих дать детям представление о символах и знаках используемых при моделировании.
знакомлю учащихся с «ключевыми» словами в тексте задачи
знакомлю учащихся с «ключевыми» словами в тексте задачи
Слайд 14«КЛЮЧЕВЫЕ» СЛОВА В ТЕКСТЕ ЗАДАЧИ
Разностное отношение
на (больше, меньше)
Кратное отношение
В … раз (больше, меньше)
Целое из равных частей
по … в каждом …,
поровну в каждом ряду …,
В одинаковых …,
… доля …
Целое из разных частей
Было
Привезли (купили, подарили, приехали, …)
Стало
Было
Уехали (продали, съели, …)
Осталось
Было … в одном …,
Было … во втором …,
Всего (вместе) …
Слайд 15применяю метод моделирования при изучении математических понятий;
веду работу по усвоению знаково-символического
языка, на котором строится модель;
систематически провожу работу по освоению моделей тех отношений, которые рассматриваются в задачах
систематически провожу работу по освоению моделей тех отношений, которые рассматриваются в задачах
Слайд 17I I этап - МОДЕЛИРОВАНИЕ
Цель: установить, что известно, что нужно
найти, как связаны между собой данные и искомое.
Слайд 18Для формирования умения моделировать задачу, я использую следующие приёмы:
Составление краткой записи
задачи при помощи опорных слов (рисунка, схемы, таблицы)
2) Выбор рисунка, схемы и т. д. к данной задаче
3) Исправление ошибок в краткой записи задачи.
4) Составление задачи по краткой записи (опорным словам, рисунку, схеме, чертежу, таблице).
5) Подбор к схеме подходящего текста из предложенных.
6) Установление взаимноодназначного соответствия – проведение «дорожек» от слова к его изображению на схеме.
2) Выбор рисунка, схемы и т. д. к данной задаче
3) Исправление ошибок в краткой записи задачи.
4) Составление задачи по краткой записи (опорным словам, рисунку, схеме, чертежу, таблице).
5) Подбор к схеме подходящего текста из предложенных.
6) Установление взаимноодназначного соответствия – проведение «дорожек» от слова к его изображению на схеме.
Слайд 19На мой взгляд, самой удачной, с этой точки зрения, моделью, является
схематический чертёж
Правильно выполненный чертёж наиболее точно отражает все взаимосвязи, о которых идёт речь в задаче. Но, к сожалению, не к каждой задаче подходит эта модель. Обычно, после анализа задачи, я предлагаю учащимся самим выбрать подходящую модель, учу находить их «плюсы» и «минусы» той или иной модели.
Правильно выполненный чертёж наиболее точно отражает все взаимосвязи, о которых идёт речь в задаче. Но, к сожалению, не к каждой задаче подходит эта модель. Обычно, после анализа задачи, я предлагаю учащимся самим выбрать подходящую модель, учу находить их «плюсы» и «минусы» той или иной модели.
Слайд 20Начинаю работу по моделированию задач с первого класса. На данном этапе
использую графические модели.
Рассматриваем некоторые виды графических моделей на примере одной задачи
Рассматриваем некоторые виды графических моделей на примере одной задачи
Слайд 21Графические модели решения задач по математике
Задача (1 кл.).
Таня
нарисовала 5 домиков, а Сережа на 4 больше. Сколько домиков нарисовал Сережа?
Слайд 22Первый подэтап:
1) Чтение текста задачи: сначала про себя, затем вслух одним
из учеников
2) Пересказ задачи своими словами
3) Представление жизненной ситуации, описанной в задаче, инсценировка этой ситуации.
2) Пересказ задачи своими словами
3) Представление жизненной ситуации, описанной в задаче, инсценировка этой ситуации.
Слайд 23Второй подэтап (графическая работа с цветом):
Разбиение текста задачи на смысловые части,
подчёркивание условия и вопроса синим и красным цветом, выделение числовых данных.
Выделение наиболее важных слов в каждой смысловой части и в вопросе задачи.
Таня нарисовала 5 домиков, а Сережа на 4 больше. Сколько домиков нарисовал Сережа?
Выделение наиболее важных слов в каждой смысловой части и в вопросе задачи.
Таня нарисовала 5 домиков, а Сережа на 4 больше. Сколько домиков нарисовал Сережа?
Слайд 25 Так для данной задачи, графическая модель может быть выполнена:
1. а) в виде рисунка
Т.-
С.-
_________?_________
Т.-
С.-
_________?_________
Слайд 31Вывод:
Каждая модель выступает как одна из форм отображения сущности задачи, помогающая
детям выстроить логическую цепочку умозаключений приводящих к конечному результату.
Слайд 32При анализе данной задачи детям предлагается сразу несколько моделей, для того,
чтобы познакомить с разными видами моделирования, во-первых. И, во-вторых, дети почти сразу определяют какая модель им «ближе». Причем делают это индивидуально, выбирая самый оптимальный вариант для себя, что дает положительный результат.
Слайд 33Анализируя какие виды моделирования труднее всего для ребят, выявила что труднее
дается запись условия в таблицу( в зависимости от класса)
Для себя наметила работу по оформлению рассуждения в таблице, в которые учащиеся записывают свои рассуждения. Эту работу делали всегда устно
сколько бизонов
сколько слонов
Для себя наметила работу по оформлению рассуждения в таблице, в которые учащиеся записывают свои рассуждения. Эту работу делали всегда устно
сколько бизонов
сколько слонов
Слайд 34Итогом своей работы считаю ВПР в 4 классе
На протяжении 3
лет ребята успешно справляются с работой
Слайд 35ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА:
1. Истомина Н. Б. Методика обучения математике в начальных классах.
– М., 1998
2. Царёва С. Е. Виды работы с задачами на уроке математики. // Начальная школа, № 10, 1990
2. Царёва С. Е. Виды работы с задачами на уроке математики. // Начальная школа, № 10, 1990
