классов
Кожаева Л. И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Копилка заданий для интеллектуального развития детей
Содержание
- 1. Копилка заданий для интеллектуального развития детей
- 2. Тематика.1. Найди закономерность.2. Задания занимательного характера.3. Проверьте
- 3. Найди закономерность.1.Перед вами ряды букв,
- 4. Ответ:
- 5. б) 1, 3, 5, 7, 9, 11, 14, 15, 17, 19.
- 6. Слайд 6
- 7. в) Рука, нос, палец, яблоко, голова.
- 8. Ответ: Яблоко.
- 9. г) А, В, Д, Ё, З, Й, К, Л, М, Н, П, С, У, Х.
- 10. Ответ: Буква К.
- 11. д) 9, 7, 4, 1, 3, 7.
- 12. Ответ:Число 4 (чётное)
- 13. е) 64, 32, 16, 12, 8, 4, 2.
- 14. Ответ: 12
- 15. ж) Сумка, саквояж, кейс, носилки, портфель.
- 16. Ответ: Носилки.
- 17. з) Какая фигура лишняя?
- 18. Ответ: Круг.
- 19. 2. Какой треугольник лишний? а)
- 20. Ответ: Под буквой Д.
- 21. 3. Лишнее слово.Воробей, дрозд, иволга, орел.
- 22. Ответ:Орел (хищник)
- 23. Токарь, грузчик, землекоп, артист, плотник.
- 24. Ответ: Артист
- 25. Подсолнух, одуванчик, сливочное масло, перегной, солнце.
- 26. Ответ: Перегной (среди всех желтых, он черный)
- 27. 4.Вместо ? поставь число. 7
- 28. Ответ: 5
- 29. 5. Какое лишнее слово?РОСИП ЕВШАЛ
- 30. Ответ: Евшал
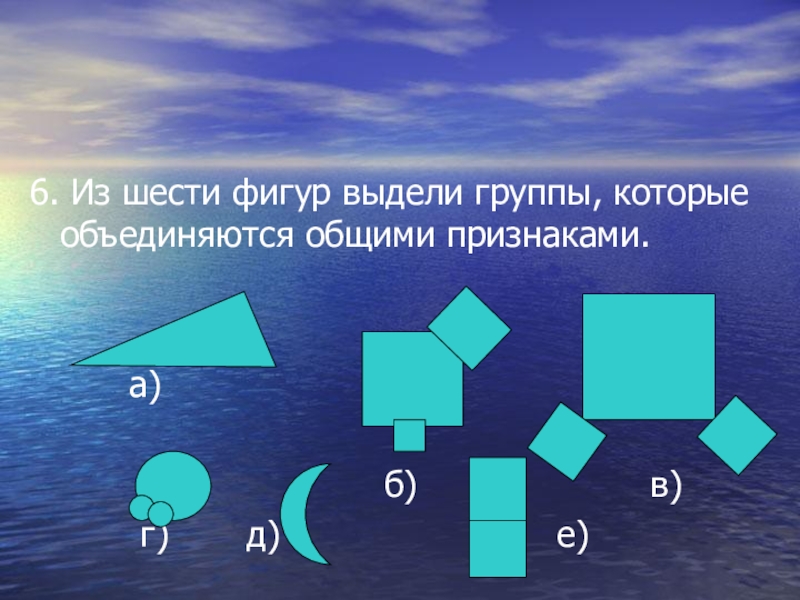
- 31. 6. Из шести
- 32. Слайд 32
- 33. 7. Вот два слова: КИТ и НЕБО.
- 34. Найдите связывающие слова для понятий:а)КОТЁНОК и ЧЕЛОВЕКб)ЛЮБОВЬ и МОРЕв)ПОВОРОТ, РАЗГОВОР и ВОПРОСг)НОЧЬ и ТУШЬд)ОВРАГ и МЫСЛЬ
- 35. Ответы:а)Ласковый.б)Безграничный.в)Трудный.г)Чёрный.д)Глубокий.
- 36. Задания занимательного характера.
- 37. Натуральные числа и действия над ними.1.
- 38. Слайд 38
- 39. Ответы:а) 51б) 80
- 40. Из цифр 3, 5, 8
- 41. Ответы:А)853Б)358
- 42. 3. Уловите закономерность в следующих рядах чисел
- 43. Ответы:1) 2, 4, 6, 8, 10, 122)1,
- 44. 4. Тестовые вопросы.На доске записано число 36.1) Назовите число:а) больше 36,б) меньше 36.
- 45. Ответы:а) 37 и далее…б) 35, 34, …
- 46. 2) Представьте число 36 в виде суммы:а)
- 47. Ответы:а) 18 + 18б) 20 + 16в) 12 +12 +12г) 9 +7 + 20
- 48. 3) Назовите дополнение числа 36:а) до 100,б) до 1000.
- 49. Ответы:а) 64б) 964
- 50. 5. Степа Смекалкин записал в тетради двузначное
- 51. Ответ:
- 52. 6. Степа Смекалкин задумал число. Потом он
- 53. Ответ:0
- 54. 7. Степа Смекалкин задумал число. Потом он
- 55. Ответ:1
- 56. 8. Подставьте вместо звездочек такие знаки действий,
- 57. Ответы:А) 4 - 4 +13 = 13Б)
- 58. 9. Игровой момент. Я задумала некоторое натуральное
- 59. Скажите, какое число я могла
- 60. Ответ:Задуманное число 14.
- 61. 10.Учитель предложил Вите Верхоглядкину решить
- 62. Ответ: На сколько тетради дороже линеек?
- 63. 2 задача. Купили 20 тетрадей по
- 64. Ответ: Что дороже: тетради или карандаши?
- 65. 11. Поставьте вместо звездочек такие знаки
- 66. Ответы:А) 15 : 3 + 2 =
- 67. Проверьте свою
- 68. Ответ: Спичку.
- 69. 2.Какое слово из 11 букв все ученики и даже учителя пишут неправильно?
- 70. Ответ:Неправильно.
- 71. 3.Еще Колумб решил знаменитую задачу: как поставить яйцо на острый конец?
- 72. Ответ: Разбил яйцо и без скорлупы легко поставил на острый конец (варёное).
- 73. 4.Можно ли пустое ведро наполнить 3
- 74. Ответ: Сначала наполнить большими камнями, потом песком, затем водой.
- 75. 5.Когда об воду можно порезать руку?
- 76. Ответ: Превратить
- 77. 6.Что находится внутри квадрата?
- 78. Ответ: Площадь.
- 79. 7.Банка с широким горлом закрыта
- 80. Ответ: Нажать на пробку сбоку, повернуть поперек и вытащить 2 пальцами.
- 81. 8.Можно ли так бросить мяч, чтобы он,
- 82. Ответ: Можно.
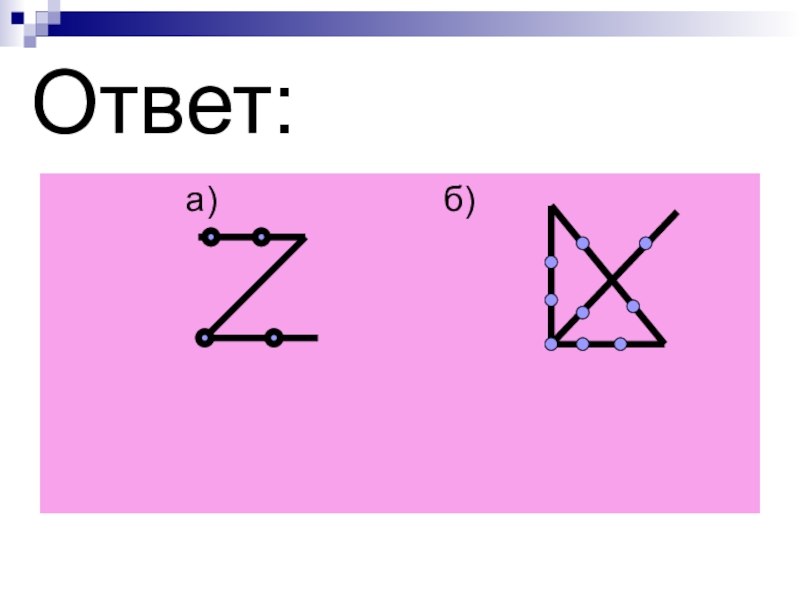
- 83. 9. а) Через 4 точки, как бы
- 84. Ответ:
- 85. 10.Два путника подошли к реке и просят
- 86. Ответ: Видимо путники подошли к реке с двух сторон, то такая переправка реальна.
- 87. 11.Вам нужно из круглого листа фанеры
- 88. Ответ: Надо круг согнуть сначала
- 89. 12.Спичку можно зажечь не только о
- 90. Ответ: Надо превратить воду в
- 91. 13.Прорицатель берется предсказать точно счет любого матча до того, как тот начнется.
- 92. Ответ:До начала встречи счет всегда 0:0.
- 93. 14.Даны весы, гири, пробка, свечка, спички, 2
- 94. Ответ: Надо поставить на чашку
- 95. 15.В каждой строчке должно получится слово.ИКС +
- 96. Из двух слов – третье.
- 97. СТРОЙ + НОГА =ЛАЙ + ШЕФ =
- 98. КАРАТ + СПИНА =ВИЛКА + АРЕСТ =СИЛОК
- 99. Ответы:
- 100. Математическая разминка
- 101. Ответ: Машина «Волга»
- 102. 2.В обувном шкафчике Мальвины 3 пары туфелек.
- 103. Ответ:
- 104. 3.Сколько нужно взять одинаковых цифр, чтобы соединить их знаком + и получить сумму, равную шести?
- 105. Ответ:
- 106. 4.На столе 4 яблока. Одно из них разрезали пополам. Сколько яблок на столе?
- 107. Ответ:
- 108. 5.У девочки столько сестер, сколько братьев. А
- 109. Ответ:
- 110. 6.Маша старше Вовы на 3 года. Маша
- 111. Ответ:
- 112. 7.Стол отстоит от шкафа на 4 метра.
- 113. Ответ:
- 114. 8.На скамейке вечерком сидели 5 мальчиков и
- 115. Ответ:
- 116. Слайд 116
- 117. 6.Английская мера длины, давшая имя героине известной
- 118. 11.Шесть квадратов на двенадцати ребрах.12.Между плюсом и минусом.13.Единица измерения углов.14.Целеустремленный отрезок.15.Дуэт в кубе.
- 119. Ответы:
- 120. Слайд 120
- 121. 6.Единица со свитой из шести нулей.7.Эту неотъемлемую
- 122. 10.Из проволоки сложили квадрат со стороной 3
- 123. Ответы:
- 124. Логические связи.Языковые пропорции.
- 125. Слайд 125
- 126. Слайд 126
- 127. Тренируем быстроту
- 128. Ответы:А) Сцена.Б) Килька.В) Песня.Г) Курага.Д) Суфлёр.
- 129. 2.Сосчитайте в уме и быстро ответьте на
- 130. Ответы:А) в 4 раза.Б) на 4.В) 207.Г) на 63.Д) 12 – Ю
- 131. 3.Как можно быстрее в каждом ряду подчеркните
- 132. Ответы:17 32 16 22
- 133. 4.В этом задании перед вами 20 чисел.
- 134. Ответы:
- 135. Занимательная математикаБлок 1.Запишите двузначное число. Которое заканчивается
- 136. Ответы:9.4 часа дня.
- 137. В прошлом году Наташа была на пол
- 138. Ответы:Сережа.Сумма четных чисел.
- 139. Расстояние от пункта А до пункта Б
- 140. Ответы:В 24 раза.Одинаковы.
- 141. Блок 2. А теперь я
- 142. 9 3 8 *
- 143. Слайд 143
- 144. Блок 3.Ответьте, пожалуйста, на следующие вопросы:1.У кошки
- 145. Ответы:1. Один (слог).2. Ни за сколько, она умрет.
- 146. 3.Три спички лежат на столе. Как удалить
- 147. Ответы:3. Надо передвинуть любую крайнюю.4. 3 метра5. 1 и 5 рублей.
- 148. 6.Имеются песочные часы на 3 и 7
- 149. Ответы:6.Опрокинуть и те, и
- 150. 8.В прямоугольном треугольнике один из углов равен
- 151. Ответы:8. 90 и 50 градусов9. Отрезок, процент.10. Острые.
- 152. 11.Сумма углов треугольника равна…12.Углы измеряются в…13.Существуют ли
- 153. Ответы:11. 180 градусам.12. Градусах.13.
- 154. 15.Назовите первые «вычислительные устройства», которыми пользовались в
- 155. Ответы:15. Пальцы рук.16. Грош, полушка.17. 11.
- 156. 18.Какой цифрой заканчивается произведение
- 157. Ответы:18. 0.19. Пифагор.20. Верста.
- 158. 21.В русских арифметиках 17 века употреблялись такие
- 159. Ответы:21. Тьма.22. Штоф, ведро.
- 160. Знаете ли вы?До Фалеса никто в Древней
- 161. В 1685 году в Париже было напечатано
- 162. При взвешивании на Руси пользовались весами двух
- 163. Иногда о росте человека говорят: «От горшка
- 164. Днем рождения первого кроссворда считается 21 декабря
- 165. Кроссворды очень быстро распространились по
- 166. Уже 27 сентября 1924 года
- 167. На сегодняшний день никто не ошибется,
- 168. Всем ясно, что всякого рода учет материальных
- 169. «Мерила торговли» включали в себя:
- 170. Знаете ли вы, что в старину большие
- 171. А эстонские моряки измеряли большие расстояния трубками
- 172. Известно, что в римской числовой системе ноль
- 173. Слово «геометрия» греческого происхождения. «Гео – земля,
- 174. Во се века математики знакомили друг друга
- 175. На протяжении веков почти в каждой стране
- 176. Например, дюйм – это длина 3
- 177. Слайд 177
Тематика.1. Найди закономерность.2. Задания занимательного характера.3. Проверьте свою сообразительность.4. Математическая разминка.5. Логические связи.6. Занимательная математика.7. Знаете ли вы?
Слайд 1«Развитие интеллектуальных способностей учащихся младшего школьного возраста на уроках математики». Учитель начальных
Слайд 2Тематика.
1. Найди закономерность.
2. Задания занимательного характера.
3. Проверьте свою сообразительность.
4. Математическая разминка.
5.
Логические связи.
6. Занимательная математика.
7. Знаете ли вы?
6. Занимательная математика.
7. Знаете ли вы?
Слайд 3 Найди закономерность.
1.Перед вами ряды букв, слов и чисел.
Подумайте какие из них выпадают из общего ряда, и объясните почему.
а) Р, А, Б, Ж, М, Щ.
а) Р, А, Б, Ж, М, Щ.
Слайд 6 Ответ:
Выпадает
число 14, т.к. каждое последующее число отличается от предыдущего на 2. Надо написать число 13.
Слайд 32 Ответы:
/б, в, г- состоят
из 3-х элементов/
/а, б, в, е- построение из прямых линий/
/б, в, е- квадраты/
/а, д- одиночные/
/г, д- круглые, дугообразные/
/а, б, в, е- построение из прямых линий/
/б, в, е- квадраты/
/а, д- одиночные/
/г, д- круглые, дугообразные/
Слайд 33
7. Вот два слова: КИТ и НЕБО.
Надо найти связывающее
их слово, т.е. такое понятие, которое подходило бы и к КИТУ и к НЕБУ.(это слово голубой)
Словом крепкий связываются такие далекие по смыслу слова, как ОРЕШЕК и ХАРАКТЕР.
Словом зеленый связываются слова КУЗНЕЧИК и ПОМИДОР, ЛЕС и ГЛАЗА.
Словом крепкий связываются такие далекие по смыслу слова, как ОРЕШЕК и ХАРАКТЕР.
Словом зеленый связываются слова КУЗНЕЧИК и ПОМИДОР, ЛЕС и ГЛАЗА.
Слайд 34
Найдите связывающие слова для понятий:
а)КОТЁНОК и ЧЕЛОВЕК
б)ЛЮБОВЬ и МОРЕ
в)ПОВОРОТ, РАЗГОВОР и
ВОПРОС
г)НОЧЬ и ТУШЬ
д)ОВРАГ и МЫСЛЬ
г)НОЧЬ и ТУШЬ
д)ОВРАГ и МЫСЛЬ
Слайд 37Натуральные числа и
действия над ними.
1. Найди число, у которого:
а) цифра
десятков больше цифры единиц в 5 раз.
б) цифра единиц на 9 меньше цифры десятков.
б) цифра единиц на 9 меньше цифры десятков.
Слайд 40
Из цифр 3, 5, 8 можно составить трехзначное число
583. В этом числе каждая цифра используется по одному разу. Какие еще трехзначные числа можно составить из данных цифр?
Какое из составленных чисел будет:
А) наибольшим,
Б) наименьшим?
Какое из составленных чисел будет:
А) наибольшим,
Б) наименьшим?
Слайд 42
3. Уловите закономерность в следующих рядах чисел и допишите по 2
числа в каждом ряду:
1) 2, 4, 6, 8, . . .
2) 1, 10, 100, . . .
3) 1, 3, 5, 7, . . .
4) 1, 2, 4, 8, . . .
1) 2, 4, 6, 8, . . .
2) 1, 10, 100, . . .
3) 1, 3, 5, 7, . . .
4) 1, 2, 4, 8, . . .
Слайд 43Ответы:
1) 2, 4, 6, 8, 10, 12
2)1, 10, 100, 1000, 10000
3)
1, 3, 5, 7, 9, 11
4) 1, 2, 4, 8, 16, 32
4) 1, 2, 4, 8, 16, 32
Слайд 46
2) Представьте число 36 в виде суммы:
а) двух равных слагаемых,
б) двух
неравных слагаемых,
в) трех равных слагаемых,
г) трех неравных слагаемых.
в) трех равных слагаемых,
г) трех неравных слагаемых.
Слайд 50
5. Степа Смекалкин записал в тетради двузначное число. Потом, переставив в
нем в нем цифры местами, получил еще одно число.
Затем он нашел разность этих чисел. В ответе получился нуль. Не могли бы вы назвать число, обладающее таким же свойством?
Затем он нашел разность этих чисел. В ответе получился нуль. Не могли бы вы назвать число, обладающее таким же свойством?
Слайд 52
6. Степа Смекалкин задумал число. Потом он умножил это число на
19 и к произведению прибавил 19. В ответе у него тоже получилось 19. Какое число задумал Степа?
Слайд 54
7. Степа Смекалкин задумал число. Потом он умножил это число на
23 и от произведения отнял число 23. В ответе у него получился 0. Какое число задумал Степа?
Слайд 56
8. Подставьте вместо звездочек такие знаки действий, чтобы равенства были верными:
А)
4 * 4 * 13=13
Б) 21 * 8 * 8=21
Б) 21 * 8 * 8=21
Слайд 58
9. Игровой момент.
Я задумала некоторое натуральное число, а вы должны
отгадать его.
Для этого один из вас называет любое число. Например 11. Я это число прибавлю к задуманному, либо отниму от задуманного числа и сообщу вам результат. На доске пишу: 11 25.
Для этого один из вас называет любое число. Например 11. Я это число прибавлю к задуманному, либо отниму от задуманного числа и сообщу вам результат. На доске пишу: 11 25.
Слайд 59
Скажите, какое число я могла задумать? Да я могла
задумать либо 14, либо 36. Чтобы вы точно узнали задуманное число, еще один ученик называет число, например 7. На доске я пишу: 7 21. Какое число я могла задумать? 14 или 28?
Слайд 61
10.Учитель предложил Вите Верхоглядкину решить следующую задачу: «Купили 20
тетрадей по 5 тенге за штуку и 2 линейки по 10 тенге за штуку. Сколько стоит вся покупка?»
Решая эту задачу, Витя составил числовое выражение: 5*20-10*2=80.
Получилось 80 тенге.
Согласны ли вы с его решением? Что вычислил Витя?
Решая эту задачу, Витя составил числовое выражение: 5*20-10*2=80.
Получилось 80 тенге.
Согласны ли вы с его решением? Что вычислил Витя?
Слайд 63
2 задача.
Купили 20 тетрадей по 3 тенге и 30
карандашей по 2 тенге. Сколько стоит вся покупка?
Витя составил числовое выражение:
3*20-2*30=0. Получился 0. Что вычислил Витя?
Витя составил числовое выражение:
3*20-2*30=0. Получился 0. Что вычислил Витя?
Слайд 65
11. Поставьте вместо звездочек такие знаки действий, чтобы выполнялся
порядок действий, указанный римскими цифрами. Можно пользоваться скобками.
I II I II III
А) 15 * 3 * 2 = 7 В) 64 * 8 * 4 *2 =4
II I
Б) 48 * 9 * 3 = 45
I II I II III
А) 15 * 3 * 2 = 7 В) 64 * 8 * 4 *2 =4
II I
Б) 48 * 9 * 3 = 45
Слайд 67 Проверьте
свою сообразительность.
1.Вы пошли в темную кухню, где есть свеча, газовая плита и керосиновая лампа. Что вы зажжете в первую очередь?
Слайд 79
7.Банка с широким горлом закрыта тонкой пробкой, слегка утопленной
в нем. Как вытащить пробку рукой?
Слайд 81
8.Можно ли так бросить мяч, чтобы он, пролетев некоторое
расстояние, остановился и начал двигаться в обратном направлении.
Слайд 82 Ответ:
Можно. Если бросить вертикально.
Мяч, поднявшись на высоту, остановится, после чего двигается обратно.
Слайд 83
9. а) Через 4 точки, как бы вершины квадрата, проведите 3
прямые линии, не отрывая карандаша от бумаги.
б) соедини 9 точек 4 прямыми.
б) соедини 9 точек 4 прямыми.
Слайд 85
10.Два путника подошли к реке и просят у бакенщика лодку, чтобы
переправиться. Тот выдвигает условие: переплывать по одному а затем лодку поставить на место. Как это сделать?
Слайд 87
11.Вам нужно из круглого листа фанеры вырезать квадрат. Как
это сделать, если у вас нет никаких измерительных инструментов, но у вас есть круг из листа бумаги.
Слайд 88Ответ:
Надо круг согнуть сначала вдвое, получится угол
180° , затем вчетверо, получится угол 90°- прямой угол.
Слайд 89
12.Спичку можно зажечь не только о спичечный коробок, но и
о стекло, дерево, бумагу, керамику и пр. А как с помощью воды зажечь спичку и не только спичку, даже развести костер?
Слайд 93
14.Даны весы, гири, пробка, свечка, спички, 2 дощечки, ножницы, умывальник. Как
сделать так, чтобы минуту весы находились в равновесии, а потом нарушить их равновесие, не прикасаясь к ним и к тому что есть на их чашках? Никакие другие предметы брать нельзя.
Слайд 94Ответ:
Надо поставить на чашку весов свечку, уравновесить
их гирями, а потом зажечь. Сгорев, она нарушит равновесие.
Слайд 95
15.В каждой строчке должно получится слово.
ИКС + Р
ИКС + РА
ИКС +
РА + Т
ИКС + РА + ТА
ИКС + РА + ТА + Н
ИКС + РА + ТА + НА
ИКС + РА + ТА
ИКС + РА + ТА + Н
ИКС + РА + ТА + НА
Слайд 96
Из двух слов – третье.
Путем перестановки букв
составить третье, новое слово – имя существительное. Все буквы должны быть использованы. Например, из слов ЕЛИ и МАЯК = КАМЕЛИЯ
Слайд 98
КАРАТ + СПИНА =
ВИЛКА + АРЕСТ =
СИЛОК + ПУНШ =
БУМ +
АРА =
РИС + КАТ =
ВОДА + СОРОК =
ШАР + ЧАД =
ВАЛ + САН =
РИС + КАТ =
ВОДА + СОРОК =
ШАР + ЧАД =
ВАЛ + САН =
Слайд 100Математическая разминка
Блок 1.
1.В Москву из Киева в одно и то же время прибыли «Волга» и «Жигули». «Волга» ехала медленнее, чем «Жигули». Какая машина выехала раньше из Киева?
1.В Москву из Киева в одно и то же время прибыли «Волга» и «Жигули». «Волга» ехала медленнее, чем «Жигули». Какая машина выехала раньше из Киева?
Слайд 102
2.В обувном шкафчике Мальвины 3 пары туфелек. В темноте она наугад
берет 4 туфельки. Окажется ли при этом вытянутой пара одинаковой обуви?
Слайд 104
3.Сколько нужно взять одинаковых цифр, чтобы соединить их знаком + и
получить сумму, равную шести?
Слайд 108
5.У девочки столько сестер, сколько братьев. А ее брат сказал, что
у нее 3 сестры. Сколько детей в семье?
Слайд 112
7.Стол отстоит от шкафа на 4 метра. Сколько метров будет между
ними, если шкаф передвинуть вправо на 2 метра, а стол влево на столько же?
Слайд 114
8.На скамейке вечерком сидели 5 мальчиков и 3 девочки. После предложения
мамы одного из ребят пойти в кино Света, Алена и Марина ушли. Сколько мальчиков и сколько девочек остались болтать на скамейке?
Слайд 116
Блок 2.
1.Предмет для демонстрации симметрии.
2.Цифровой знак, обозначающий отсутствие величины.
3.Чему равен вес соли, которую надо съесть, чтобы хорошо узнать человека?
4.Приплюснутый круг.
5.Какой параметр нужно знать, чтобы найти площадь круга?
1.Предмет для демонстрации симметрии.
2.Цифровой знак, обозначающий отсутствие величины.
3.Чему равен вес соли, которую надо съесть, чтобы хорошо узнать человека?
4.Приплюснутый круг.
5.Какой параметр нужно знать, чтобы найти площадь круга?
Слайд 117
6.Английская мера длины, давшая имя героине известной сказки.
7.Последовательница нуля.
8.Параллелограмм с равными
сторонами.
9.Сера земельной площади, являющаяся анаграммой слова РАК.
10.Заменитель числа 1 при счете.
9.Сера земельной площади, являющаяся анаграммой слова РАК.
10.Заменитель числа 1 при счете.
Слайд 118
11.Шесть квадратов на двенадцати ребрах.
12.Между плюсом и минусом.
13.Единица измерения углов.
14.Целеустремленный
отрезок.
15.Дуэт в кубе.
15.Дуэт в кубе.
Слайд 120
Блок 3.
1.Линейка, которой любой угол по плечу?
2.Когда 25 километров умещаются в одном сантиметре?
3.Эта геометрическая фигура в цирке становится гимнастическим снарядом.
4.Нахождение неизвестного.
5.Сколько граней у шестигранного карандаша?
1.Линейка, которой любой угол по плечу?
2.Когда 25 километров умещаются в одном сантиметре?
3.Эта геометрическая фигура в цирке становится гимнастическим снарядом.
4.Нахождение неизвестного.
5.Сколько граней у шестигранного карандаша?
Слайд 121
6.Единица со свитой из шести нулей.
7.Эту неотъемлемую часть геометрической фигуры можно
превратить в полезное ископаемое при помощи мягкого знака.
8.На геометрическом теле этой формы стоит девочка на известной картине Пикассо. Какую скорость во время полета развивает птица эму?
9.Где сумма углов больше: в квадрате или в ромбе?
8.На геометрическом теле этой формы стоит девочка на известной картине Пикассо. Какую скорость во время полета развивает птица эму?
9.Где сумма углов больше: в квадрате или в ромбе?
Слайд 122
10.Из проволоки сложили квадрат со стороной 3 сантиметра, затем проволоку разогнули
и составили из нее треугольник. Чему равна длина всех его сторон? А одной стороны, если он будет равносторонним?
11.Что такое жидкий килограмм?
12.Наименьшее четырехзначное число.
13.Вопрос для решения.
11.Что такое жидкий килограмм?
12.Наименьшее четырехзначное число.
13.Вопрос для решения.
Слайд 124 Логические связи.
Языковые пропорции.
- дом
/ крыша = человек / …
- турнир / медаль = … / премия
- камень / гора = слово / …
- бумага/рисунок = /отражение
- автомобиль/шины = конь/…
- рыба/аквариум = тигр/…
- верблюд/горб = …/сумка
- человек/пища = машин
- школа/буфет = дом/…
- турнир / медаль = … / премия
- камень / гора = слово / …
- бумага/рисунок = /отражение
- автомобиль/шины = конь/…
- рыба/аквариум = тигр/…
- верблюд/горб = …/сумка
- человек/пища = машин
- школа/буфет = дом/…
Слайд 125
Объединение в 2 группы.
- трамвай, электричка, автобус, троллейбус, мотоцикл, автомобиль.
- берлога, хата, гнездо, нора, юрта, сакля.
- роза, василёк, ромашка, гладиолус, ландыш, астра.
- свинья, олень, корова, овца, лиса, волк смородина.
- Незнайка, Тимур, Гек, Тюбик, Чук, Шпунтик.
- мама, сын, свекровь, тесть, папа, тётя.
- лимон, яблоко, груша, слива, мандарин, апельсин.
- трамвай, электричка, автобус, троллейбус, мотоцикл, автомобиль.
- берлога, хата, гнездо, нора, юрта, сакля.
- роза, василёк, ромашка, гладиолус, ландыш, астра.
- свинья, олень, корова, овца, лиса, волк смородина.
- Незнайка, Тимур, Гек, Тюбик, Чук, Шпунтик.
- мама, сын, свекровь, тесть, папа, тётя.
- лимон, яблоко, груша, слива, мандарин, апельсин.
Слайд 126
Логические ошибки.
- На
автобусной остановке стояли люди, старики, дети.
- Дела его бизнеса шли хорошо.
- Я не знаю, какую профессию выбрать- стюардессы или бортпроводницы.
- Лётчик - это пилот авиалайнера.
- Мне досталась лишь одна пара из двух сапог.
- Дела его бизнеса шли хорошо.
- Я не знаю, какую профессию выбрать- стюардессы или бортпроводницы.
- Лётчик - это пилот авиалайнера.
- Мне досталась лишь одна пара из двух сапог.
Слайд 127 Тренируем быстроту реакции
1.Выполните математические действия
и прочитайте слова:
А) ПРИ + С – РИ + ЦЕ – П + НА =
Б) СОК + ИЛ – СО + ЬКУ – У + А =
В) ПЕРО + СИ – РО + НО – И + Я =
Г) АК + ПУ – АП + ДРА + Г – Д + А =
Д) СУД + ФЕЯ – ДЕ + ЛЁ – Я + РЕ – Е =
А) ПРИ + С – РИ + ЦЕ – П + НА =
Б) СОК + ИЛ – СО + ЬКУ – У + А =
В) ПЕРО + СИ – РО + НО – И + Я =
Г) АК + ПУ – АП + ДРА + Г – Д + А =
Д) СУД + ФЕЯ – ДЕ + ЛЁ – Я + РЕ – Е =
Слайд 129
2.Сосчитайте в уме и быстро ответьте на вопросы:
А)Во сколько раз
25 меньше 100?
Б)На сколько нужно умножить 39, чтобы получить 156?
В)Чему равно частное от деления 1656 на 8?
Г)На сколько 100 больше чем, 37?
Д)Какую часть от часа составляют 5 минут?
Б)На сколько нужно умножить 39, чтобы получить 156?
В)Чему равно частное от деления 1656 на 8?
Г)На сколько 100 больше чем, 37?
Д)Какую часть от часа составляют 5 минут?
Слайд 131
3.Как можно быстрее в каждом ряду подчеркните все числа, кратные тому,
которое стоит в конце строчки:
17 32 16 22 9 5 12 28 4
28 12 10 37 42 61 63 14 7
19 13 36 72 21 14 54 17 9
25 17 21 45 19 31 51 10 3
17 32 16 22 9 5 12 28 4
28 12 10 37 42 61 63 14 7
19 13 36 72 21 14 54 17 9
25 17 21 45 19 31 51 10 3
Слайд 132 Ответы:
17 32 16 22 9 5 12
28 4
28 12 10 37 42 61 63 14 7
19 13 36 72 21 14 54 17 9
25 17 21 45 19 31 51 10 3
28 12 10 37 42 61 63 14 7
19 13 36 72 21 14 54 17 9
25 17 21 45 19 31 51 10 3
Слайд 133
4.В этом задании перед вами 20 чисел. Постарайтесь разбить их на
10 пар так, чтобы сумма чисел каждой пары равнялась 83. Например, 50 + 33 = 83. Эту работу вы должны выполнять в уме, записывая лишь ответы. Подумайте, как устроить выполнение этой работы? Как действовать наиболее рационально?
30 44 27 12 49 35 53 21 6 62
56 48 71 58 65 39 77 18 25 34
30 44 27 12 49 35 53 21 6 62
56 48 71 58 65 39 77 18 25 34
Слайд 135Занимательная
математика
Блок 1.
Запишите двузначное число. Которое заканчивается цифрой 0 и делится на
5 без остатка. Сколько всего таких чисел?
– Который час? – спросила дочь у мамы.
– Давай посчитаем вместе: 10 часов тому назад от начала суток прошло столько же времени, сколько останется до конца суток через 2 часа. Так который час?
– Который час? – спросила дочь у мамы.
– Давай посчитаем вместе: 10 часов тому назад от начала суток прошло столько же времени, сколько останется до конца суток через 2 часа. Так который час?
Слайд 137
В прошлом году Наташа была на пол года моложе Сережи. Кто
из них будет старше в следующем году?
Что больше и на сколько: сумма всех четных или сумма всех нечетных чисел от 1 до 10?
Что больше и на сколько: сумма всех четных или сумма всех нечетных чисел от 1 до 10?
Слайд 139
Расстояние от пункта А до пункта Б самолет пролетает за 5
часов, а поезду для этого требуется 5 суток. Во сколько раз быстрее можно преодолеть путь А – Б на самолете?
Что больше: половина четверти какого-либо числа или четверть его половины?
Что больше: половина четверти какого-либо числа или четверть его половины?
Слайд 141
Блок 2.
А теперь я хочу предложить вам задание
из серии «Сбежали цифры».Внимательно посмотрите на следующие примеры и , пожалуйста, постарайтесь выявить закономерность в «убегании цифр». Проанализировав ситуацию, восполните пробелы в записи(математических действиях и цифрах). Подумайте, с чего надо начинать выполнение задания и почему.
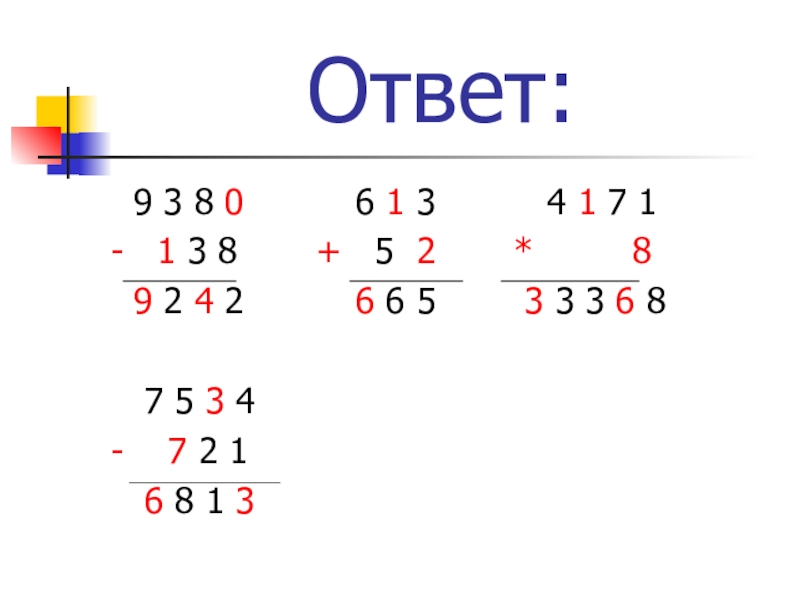
Слайд 143 Ответ:
9 3 8
0 6 1 3 4 1 7 1
- 1 3 8 + 5 2 * 8
9 2 4 2 6 6 5 3 3 3 6 8
7 5 3 4
- 7 2 1
6 8 1 3
- 1 3 8 + 5 2 * 8
9 2 4 2 6 6 5 3 3 3 6 8
7 5 3 4
- 7 2 1
6 8 1 3
Слайд 144
Блок 3.
Ответьте, пожалуйста, на следующие вопросы:
1.У кошки их два, у собаки
и коровы – три, а сколько их у дога?
2.Известно, что гусеница живет не более суток, а затем превращается в кокон. Одна гусеница с 6 часов утра до 6 часов вечера забирается на двенадцатиметровое дерево до отметки 5 метров, а за ночь спускается на 2 метра. Через сколько дней при таком движении оно достигнет верхушки дерева?
2.Известно, что гусеница живет не более суток, а затем превращается в кокон. Одна гусеница с 6 часов утра до 6 часов вечера забирается на двенадцатиметровое дерево до отметки 5 метров, а за ночь спускается на 2 метра. Через сколько дней при таком движении оно достигнет верхушки дерева?
Слайд 146
3.Три спички лежат на столе. Как удалить среднюю спичку из середины,
не трогая ее?
4.Расстояние между столом и креслом – 3 метра. Сколько метров будет между ними, если и стол, и кресло передвинуть на 2 метра вправо?
5.У Сережи в кармане две монеты на сумму 6 рублей. Одна из монет не пятирублевая. Какие это монеты?
4.Расстояние между столом и креслом – 3 метра. Сколько метров будет между ними, если и стол, и кресло передвинуть на 2 метра вправо?
5.У Сережи в кармане две монеты на сумму 6 рублей. Одна из монет не пятирублевая. Какие это монеты?
Слайд 148
6.Имеются песочные часы на 3 и 7 минут. Надо опустить яйцо
в кипящую воду ровно на 4 минуты. Как это сделать при помощи имеющихся часов?
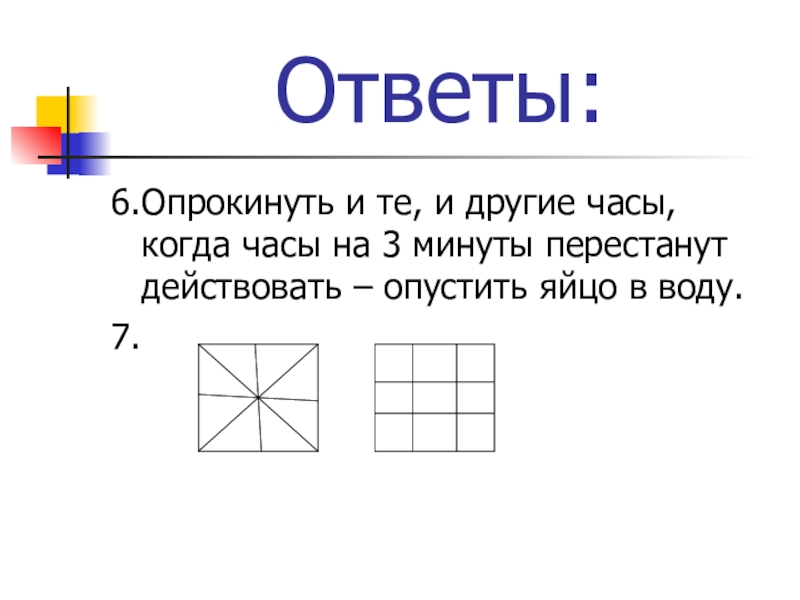
7.На сколько равных частей можно разделить квадрат четырьмя прямыми линиями?
7.На сколько равных частей можно разделить квадрат четырьмя прямыми линиями?
Слайд 149 Ответы:
6.Опрокинуть и те, и другие часы, когда часы
на 3 минуты перестанут действовать – опустить яйцо в воду.
7.
7.
Слайд 150
8.В прямоугольном треугольнике один из углов равен 40 градусам, чему равны
два других угла?
9.Как это называется:
– часть прямой, соединяющая две точки?
– сотая часть числа?
10.Один из углов треугольника тупой. Каковы остальные?
9.Как это называется:
– часть прямой, соединяющая две точки?
– сотая часть числа?
10.Один из углов треугольника тупой. Каковы остальные?
Слайд 152
11.Сумма углов треугольника равна…
12.Углы измеряются в…
13.Существуют ли треугольники с двумя прямыми
углами?
14.На памятнике древнегреческому математику Диофанту имеется надпись: «Прохожий! Под этим камнем покоится прах Диофанта, умершего в старости. Шестую часть его жизни заняло детство, двенадцатую – отрочество, седьмую – юность. Затем он женился, и через пять лет у него родился сын, который прожил вдвое меньше отца. Четыре года, до самой своей кончины, Диофант оплакивал сына». Сколько лет жил Диофант?
14.На памятнике древнегреческому математику Диофанту имеется надпись: «Прохожий! Под этим камнем покоится прах Диофанта, умершего в старости. Шестую часть его жизни заняло детство, двенадцатую – отрочество, седьмую – юность. Затем он женился, и через пять лет у него родился сын, который прожил вдвое меньше отца. Четыре года, до самой своей кончины, Диофант оплакивал сына». Сколько лет жил Диофант?
Слайд 153 Ответы:
11. 180 градусам.
12. Градусах.
13. Нет.
14. Он прожил 84
года. Если принять всю жизнь Диофанта за X, то нужно решить следующее уравнение:
(X/6 + X/12 + X/7) + 5 + X/2 + 4 = X
(X/6 + X/12 + X/7) + 5 + X/2 + 4 = X
Слайд 154
15.Назовите первые «вычислительные устройства», которыми пользовались в древности люди.
16.В старину на
Руси пользовались монетами достоинством меньше одной копейки. Как называлась половина копейки и четвертая часть?
17.Найдите наименьше число, которое при делении на 2 даст в остатке 1, при делении на 3 – в остатке 2, при делении на 4 – в остатке 3?
17.Найдите наименьше число, которое при делении на 2 даст в остатке 1, при делении на 3 – в остатке 2, при делении на 4 – в остатке 3?
Слайд 156
18.Какой цифрой заканчивается произведение
13*14*15*16*17?
19.Как звали древнегреческого математика и философа, которому приписывают создание учения о числах четных и нечетных, простых и составных? Он доказал теорему, носящую его имя, о соотношении длин сторон прямоугольного треугольника.
20. Как называлась русская мера длины, равная 1,0668 км? Эта мера упоминалась в стихотворении А. С. Пушкина «Зимняя дорога».
19.Как звали древнегреческого математика и философа, которому приписывают создание учения о числах четных и нечетных, простых и составных? Он доказал теорему, носящую его имя, о соотношении длин сторон прямоугольного треугольника.
20. Как называлась русская мера длины, равная 1,0668 км? Эта мера упоминалась в стихотворении А. С. Пушкина «Зимняя дорога».
Слайд 158
21.В русских арифметиках 17 века употреблялись такие наименования для больших чисел:
1
000 – тысяща
10 000 – ?
100 000 – легион
Как же назывались 10 000?
22.Как назывались:
– старорусская мера объема жидкости, равная 1,23 литра, или 10 чаркам;
– старорусская мера жидкостей, равная 12,3 литра?
10 000 – ?
100 000 – легион
Как же назывались 10 000?
22.Как назывались:
– старорусская мера объема жидкости, равная 1,23 литра, или 10 чаркам;
– старорусская мера жидкостей, равная 12,3 литра?
Слайд 160Знаете ли вы?
До Фалеса никто в Древней Греции серьезно геометрией не
занимался, и у геометрических фигур не было названий. Греки стали называть фигуры словами, обозначавшими окружающие их предметы похожей формы. Так, например, для прокатки белья женщины применяли скалку, которая по-гречески называлась каландер (kylinde – с греч. катаю, вращаю). Поэтому все вытянутые тела с округлыми сечениями получили название ЦИЛИНДР.
Слайд 161В 1685 году в Париже было напечатано руководство по коммерческой арифметике
Де ла Порта. Наборщик ошибся и вместо латинского слова «cto» напечатал % ( в рукописях pro centum заменяли cento – сто и писали сокращенно cto ). На основании этого места в книге авторы стали употреблять знак % для обозначения процентов, и с середины девятнадцатого века он получил всеобщее признание.
Слайд 162При взвешивании на Руси пользовались весами двух типов. Весы с подвижной
точкой опоры и неподвижной гирей называли безменом. А в Новгороде чашечные весы называли скалвой. Известно, что немецкие купцы, торговавшие с Новгородом, требовали, чтобы все товары взвешивали на скалве. Не потому ли сегодня человека, готового на ссору из-за мелких расчетов, называют сквалыгой?
Слайд 163Иногда о росте человека говорят: «От горшка два вершка». А что
такое вершок? Это 4,45 см. Два взвешивания золота применяли золотники, составляющие одну девяносто шестую долю фунта. Отсюда происходит поговорка «Мал золотник да дорог».
Слайд 164Днем рождения первого кроссворда считается 21 декабря 1913 года, когда автору
этого вида головоломок – американскому журналисту Артуру Уинну, в свое время эмигрировавшему из Ливерпуля в Америку, было поручено к рождественским праздникам подготовить развлекательное приложение «Fan» к газете «New-York World». Первый кроссворд представлял собой ромб размером 13х13 клеток с центральной выемкой 5х5 клеток и использовал 32 слова.
Слайд 165 Кроссворды очень быстро распространились по миру и стали чрезвычайно
популярным времяпровождением множества людей. Событием стал выход в 1923 году в США первого сборника кроссвордов, изданного тиражом в 750 тысяч экземпляров и раскупленного буквально за несколько дней.
Слайд 166 Уже 27 сентября 1924 года члены «Американской лиги любителей
кроссвордов» сформулировали основные правила составления кроссвордов, которые действуют в основном и по ныне.
Слайд 167 На сегодняшний день никто не ошибется, если скажет, что кроссворды
являются самым популярным видом словесных развлечений практически во всем мире. Во многих странах даже проводятся чемпионаты по кроссвордам.
Слайд 168Всем ясно, что всякого рода учет материальных ценностей нуждается в стандартных
мерах измерения. И русские люди неоднократно разрабатывали такие эталоны.
Так, в 1136 году новгородский князь Всеволод Мстиславич утвердил устав «О церковных судах и людях и о мерилах торговли». Предварительно этот документ обсуждался представителями духовных и светских властей Господина Великого Новгорода.
Так, в 1136 году новгородский князь Всеволод Мстиславич утвердил устав «О церковных судах и людях и о мерилах торговли». Предварительно этот документ обсуждался представителями духовных и светских властей Господина Великого Новгорода.
Слайд 169 «Мерила торговли» включали в себя: «пуд медовый, гривну рублевую,
локоть еваньский». Всем торговым людям предписывалось «торговые весы и мерила блюсти без пакости», за нарушения предусматривались наказания вплоть до «предания смерти». Сами эталоны хранились в церкви Евань (Ивана) на окопах. Таким образом, храм этот использовался(помимо молитв) и в качестве палаты мер и весов.
Слайд 170Знаете ли вы, что в старину большие расстояния измеряли днями передвижения
или переходами? Так, например, в рассказе Джека Лондона «Белое безмолвие» один из индейцев, на вопрос о том, сколько еще осталось проехать, ответил: «Едешь десять снов, двадцать снов…»
Слайд 171А эстонские моряки измеряли большие расстояния трубками (то есть расстояние, за
которое можно выкурить набитую табаком трубку). В Японии же единицей измерения пути был башмак, заменявший в этой стране подкову (путь, который до полного износа подковы могла пройти лошадь).В Испании же мерой расстояния по аналогии со сказанным была сигара.
Слайд 172Известно, что в римской числовой системе ноль отсутствовал. Его ввели индийские
математики примерно в 600 году до н.э. Понятие «отрицательное число» первым использовал итальянский купец Пизано в 1202 году, обозначая им свои убытки и долги. Знакомые нам математические знаки «плюс» и «минус» впервые появились в учебнике «Правила алгебры» (1486 г.) чешского математика Яна Видмана. До этого действия сложения и вычитания обозначались начальными буквами от латинских слов «PLUS» и «MINUS».
Слайд 173Слово «геометрия» греческого происхождения. «Гео – земля, «метрео» – измеряю. Зародилась
геометрия в Древнем Египте около 2000 лет до н.э., то есть четыре тысячи лет назад. Египетский фараон разделил землю, дав каждому египтянину небольшой участок, и фараону платили налог за землю. Но так как река Нил, часто выходя из берегов, заливая участки, фараон посылал землемеров, чтобы установить, насколько уменьшился участок и какой теперь брать налог. Так в Египте возникла геометрия. Позднее о ней узнали в Древней Греции.
Слайд 174Во се века математики знакомили друг друга с условиями доказанных ими
теорем, прежде чем опубликовать доказательства для общего сведения. Это считалось данью уважения к равному или старшему.
Архимед поддерживал переписку со многими учеными и , по обычаю того времени, посылал им для доказательства свои новые теоремы. Но, судя по различным источникам, ни один из них не смог повторить его открытий.
Архимед поддерживал переписку со многими учеными и , по обычаю того времени, посылал им для доказательства свои новые теоремы. Но, судя по различным источникам, ни один из них не смог повторить его открытий.
Слайд 175На протяжении веков почти в каждой стране возникали и существовали самостоятельные
единицы измерения. Их просто-напросто назначил очередной фараон, князь, король или царь, который объяснил, что отныне его подданные должны измерять длину по размеру его руки или ноги. Такая имперская система мер хранит много любопытных сведений о произвольно выбранных единицах измерения.
Слайд 176 Например, дюйм – это длина 3 ячменных зернышек, уложенных концами
друг к другу; ярд – расстояние от носа короля Генри 1 до кончиков его царственной длани; миля – расстояние, которое проходит римский легион, делая 1000 двойных шагов. Тысячи лет люди строили дома, соборы, мосты, дороги, используя меры, происходившие от частей человеческого тела: фут (стопа), локоть, пядь и другие.
Декрет о введении метрической системы мер появился 7 апреля 1791 года во Франции. За единицу длины был принят метр (от греч. «метрон» – мера) – десятимиллионная часть одной четверти длины парижского меридиана.
Декрет о введении метрической системы мер появился 7 апреля 1791 года во Франции. За единицу длины был принят метр (от греч. «метрон» – мера) – десятимиллионная часть одной четверти длины парижского меридиана.