Ивановна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по черчению Графические построения
Содержание
- 1. Презентация по черчению Графические построения
- 2. Деление отрезков прямых на равные части 1
- 3. Деление отрезков прямых на равные части 2
- 4. Деление углов на 2 равные частиДля того
- 5. Деление прямого угла на три частиДеление прямого
- 6. Деление окружности на 3 частиСтавим ножку циркуля
- 7. Деление окружности на 4 и 8 частейДва
- 8. Деление окружности на шесть частейРаствором циркуля, равным
- 9. Деление окружности на двенадцать частейРаствором циркуля, равным
- 10. Домашнее заданиеСредний уровень «3» балла Выполнить задание
- 11. Домашнее задание Достаточный уровень «4» балла
- 12. Домашнее заданиеВысокий уровень «5»
Деление отрезков прямых на равные части 1 способ Разделить отрезок пополам можно при помощи циркуля, построив срединный перпендикуляр . Для этого берём радиус размером более половины длины отрезка и из его концов по обе стороны проводим
Слайд 1ГРАФИЧЕСКИЕ ПОСТРОЕНИЯ
Подготовила учитель черчения
Муниципальной общеобразовательной организации
« Харцызская средняя школа №5»
Жовтобрюх Светлана
Слайд 2Деление отрезков прямых на равные части
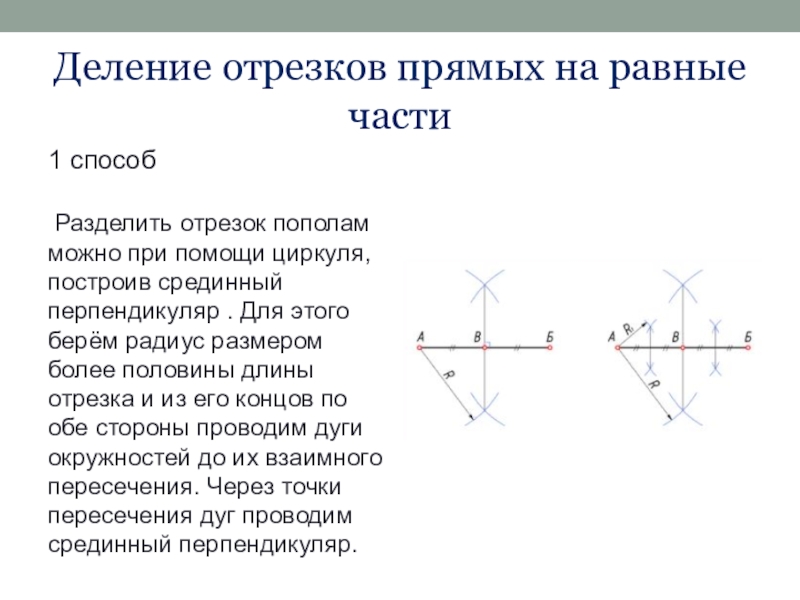
1 способ
Разделить отрезок пополам
можно при помощи циркуля, построив срединный перпендикуляр . Для этого берём радиус размером более половины длины отрезка и из его концов по обе стороны проводим дуги окружностей до их взаимного пересечения. Через точки пересечения дуг проводим срединный перпендикуляр.
Слайд 3Деление отрезков прямых на равные части
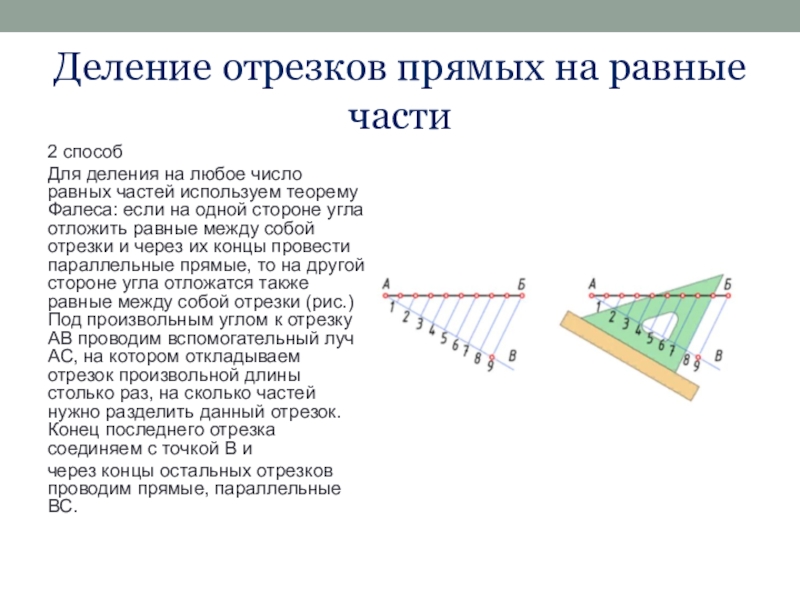
2 способ
Для деления на любое
число равных частей используем теорему Фалеса: если на одной стороне угла отложить равные между собой отрезки и через их концы провести параллельные прямые, то на другой стороне угла отложатся также равные между собой отрезки (рис.) Под произвольным углом к отрезку АВ проводим вспомогательный луч АС, на котором откладываем отрезок произвольной длины столько раз, на сколько частей нужно разделить данный отрезок. Конец последнего отрезка соединяем с точкой В и
через концы остальных отрезков проводим прямые, параллельные ВС.
через концы остальных отрезков проводим прямые, параллельные ВС.
Слайд 4Деление углов на 2 равные части
Для того чтобы разделить угол АВС
пополам нужно провести биссектрису из вершины угла. Построение биссектрисы выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К;
Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.
Из вершины угла проводят дугу окружности произвольного радиуса r до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги радиусом R, величина которого больше половины длины дуги DF, до взаимного пересечения в точке К;
Прямая проходящая через вершину В и точку К - биссектриса данного угла т.е. делит угол на две равные части.
Слайд 5Деление прямого угла на три части
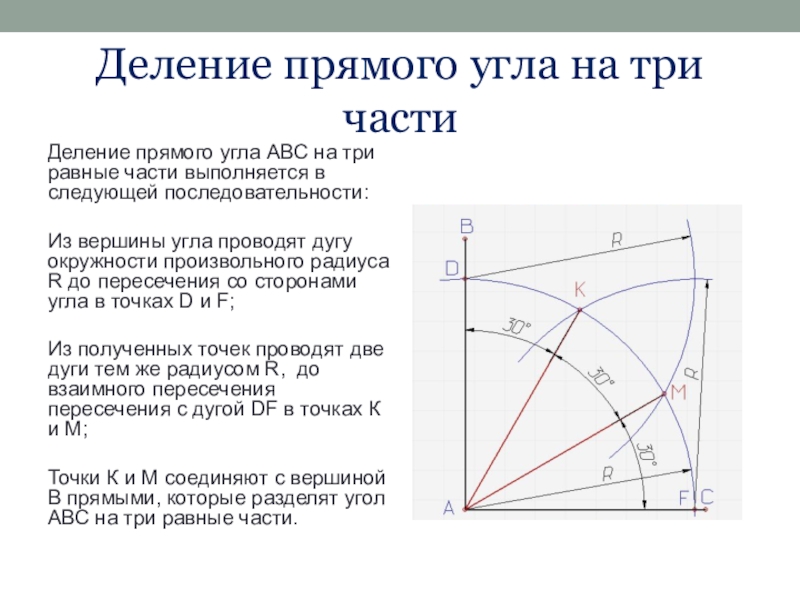
Деление прямого угла АВС на три
равные части выполняется в следующей последовательности:
Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.
Из вершины угла проводят дугу окружности произвольного радиуса R до пересечения со сторонами угла в точках D и F;
Из полученных точек проводят две дуги тем же радиусом R, до взаимного пересечения пересечения с дугой DF в точках К и М;
Точки К и М соединяют с вершиной В прямыми, которые разделят угол АВС на три равные части.
Слайд 6Деление окружности на 3 части
Ставим ножку циркуля в один из концов
взаимно перпендикулярных диаметров окружности. Раствором циркуля, равным радиусу окружности, делаем засечки на ней по обе стороны от этого конца диаметра. Получаем две вершины правильного треугольника. Третьей вершиной является противоположный конец диаметра.
Слайд 7Деление окружности на 4 и 8 частей
Два взаимно перпендикулярных диаметра делят
окружность на четыре равные части. Если через центр окружности провести прямые под углом 45ᵒ к осям, то они также разделят окружность на четыре равные части. Стороны вписанного квадрата будут параллельны осям окружности. Вместе эти два квадрата разделили окружность на восемь равных частей.
Слайд 8Деление окружности на шесть частей
Раствором циркуля, равным радиусу окружности, делаем засечки
из обоих концов одного и того же диаметра в обе стороны от них. Получаем четыре вершины правильного шестиугольника. Двумя другими вершинами являются концы диаметра, из которых сделаны
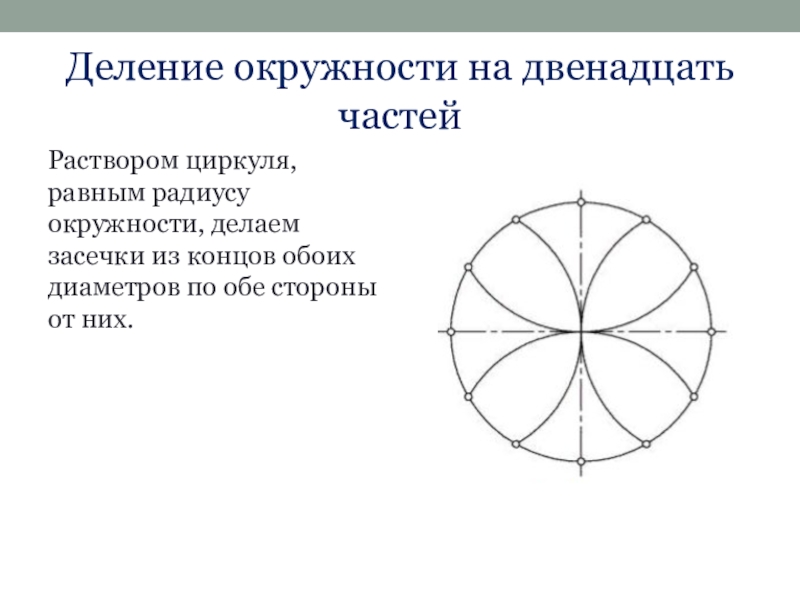
Слайд 9Деление окружности на двенадцать частей
Раствором циркуля, равным радиусу окружности, делаем засечки
из концов обоих диаметров по обе стороны от них.