- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку в 10-11 кл. Генетическое равновесие в популяциях
Содержание
- 1. Презентация к уроку в 10-11 кл. Генетическое равновесие в популяциях
- 2. Содержание Введение…………………………………………………………………………..…….…..2-31. Личности ученых……………………………………………..............4-52. Условия выполнения закона Харди-Вайнберга…........6-73.
- 3. Введение.Популяция — совокупность особей одного вида, занимающих определенный
- 4. С помощью закона Харди-Вайнберга можно вычислить степень
- 5. Личности ученых.Годфри Харолд Харди (1877–1947) – английский
- 6. Вильгельм Вайнберг (1862–1937) – немецкий врач. Изучал
- 7. Условия выполнения закона Харди-Вайнберга.Скрещивание в популяции
- 8. Эти положения вестественных условияхнарушаются:Мутации происходят всегда.Существуют миграции
- 9. Закон Харди-Вайнберга ― основной закон популяционной генетики.Закон
- 10. Пересчет на число особей.Если известны относительные частоты
- 11. Пример применения закона.Предположим, что в популяции лисов
- 12. Решетка Пеннета.11
- 13. 12
- 14. Слайд 14
- 15. Те же самые расчеты можно произвести, не
- 16. Основные положения.Частоты аллелей не изменяются от поколения
- 17. Практическое значение закона Харди-Вайнберга.В здравоохранении – позволяет
- 18. Альбинизм – это аутосомно-рецессивное заболевание. В большинстве
- 19. 18
- 20. Заключение. С помощью формулы Харди-Вайнберга можно определить ожидаемые
- 21. Спасибо за внимание!
- 22. Список использованной литературы.1. Айала Ф., Кайгер Дж. Современная
Слайд 1
УЧИТЕЛЬ: ЕГОРОВА Т.В.
ГБОУ ШКОЛЫ № 578
САНКТ-ПЕТЕРБУРГ
2014 Г.
Генетическое равновесие популяций.
Закон
Слайд 2Содержание
Введение…………………………………………………………………………..…….…..2-3
1. Личности ученых……………………………………………..............4-5
2. Условия выполнения закона Харди-Вайнберга…........6-7
3. Закон Харди-Вайнберга ― основной
4. Основные положения………………………………………...…….....15
5. Практическое значение
закона Харди Вайнберга…………………………………….....14-18
Заключение……………………………………………………………………………………19
Список использованной литературы...........................................21
1
Слайд 3Введение.
Популяция — совокупность особей одного вида, занимающих определенный ареал обитания, свободно скрещивающихся
Генетическая структура популяций определяется соотношением аллелей и генов, естественным отбором и факторами эволюции, влияющих на это соотношение.
2
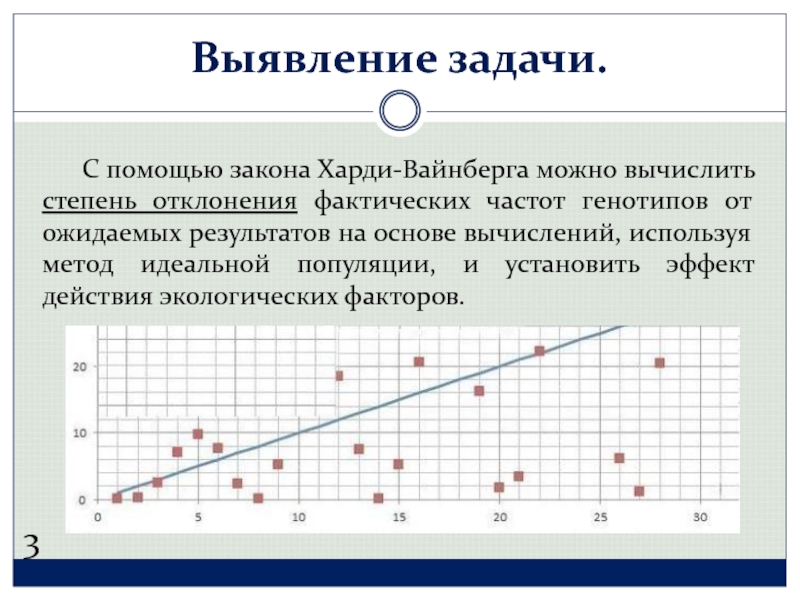
Слайд 4 С помощью закона Харди-Вайнберга можно вычислить степень отклонения фактических частот генотипов
Выявление задачи.
3
Слайд 5Личности ученых.
Годфри Харолд Харди (1877–1947) – английский математик, известный своими работами
Самую большую известность Харди принесли совместные работы с Джоном Идензором Литлвудом и с индийским математиком Cриниваса Рамануджаном.
4
Слайд 6Вильгельм Вайнберг (1862–1937) – немецкий врач. Изучал медицину в Тюбингене и
Большую часть жизни провел в изучении медицинской статистики и генетики человека, включая проблемы изучения близнецов, мутаций, и приложения законов наследования в популяциях.
Личности ученых.
5
Слайд 7Условия выполнения закона
Харди-Вайнберга.
Скрещивание в популяции случайно.
Не должно быть естественного отбора.
Не должно быть мутаций.
Не должно быть миграций как в популяцию, так и из нее.
Популяция должна иметь большую численность.
6
Слайд 8Эти положения в
естественных условиях
нарушаются:
Мутации происходят всегда.
Существуют миграции – поток генов.
Популяция состоит
В популяции существует избирательность при образовании
брачных пар, при встрече гамет и образования зигот.
Всегда существуют различия в приспособленностях и способности к выживанию.
7
Слайд 9Закон Харди-Вайнберга ― основной закон популяционной генетики.
Закон Харди-Вайнберга гласит, что в
(pA + qa)2 = р2АА + 2рq Aa + q2aa = 1
где буквам обозначены :
р – частота встречаемости аллеля А;
q – частота встречаемости аллеля а;
q2 – частота встречаемости генотипа аа;
р2 – частота встречаемости генотипа АА;
рq – частота встречаемости генотипа Аа.
8
Слайд 10Пересчет на число особей.
Если известны относительные частоты аллелей p и q
p2AA · Nобщ + 2pqAa · Nобщ + q2aa · Nобщ = Nобщ
В данном уравнении:
p2 AA · Nобщ – ожидаемая абсолютная частота (численность) доминантных гомозигот АА
2·p·q Aa · Nобщ – ожидаемая абсолютная частота (численность) гетерозигот Аа
q2 aa · Nобщ – ожидаемая абсолютная частота (численность) рецессивных гомозигот а
9
Слайд 11Пример применения закона.
Предположим, что в популяции лисов частота встречаемости аллелей А,
рА = 0,9 ,
а частота встречаемости аллелей а, обуславливающих черно-бурую окраску равна
qа = 0,1.
Слайд 15Те же самые расчеты можно произвести, не составляя таблицы, по закону
(0,9 + 0,1)2 = 0,81 + 0,18 + 0,01 = 1
или в пересчете на число особей:
(0,9 · 100 + 0,1· 100)2 = 81 + 18 + 1 = 100
14
Слайд 16Основные положения.
Частоты аллелей не изменяются от поколения к поколению.
Равновесные частоты
Равновесные частоты генотипов достигаются за одно поколение. Какими бы они не были, частоты генотипов потомков будут р2, 2рq , q2 .
15
Слайд 17Практическое значение закона Харди-Вайнберга.
В здравоохранении – позволяет оценить популяционный риск генетических
В селекции – позволяет выявить генетический потенциал исходного материала (популяций, сортов и пород селекции). [18]
В экологии – позволяет выявить влияние факторов на популяции по отклонениям фактических частот генотипов от расчетных величин. (При этом нужно соблюдать принцип единственного различия).
16
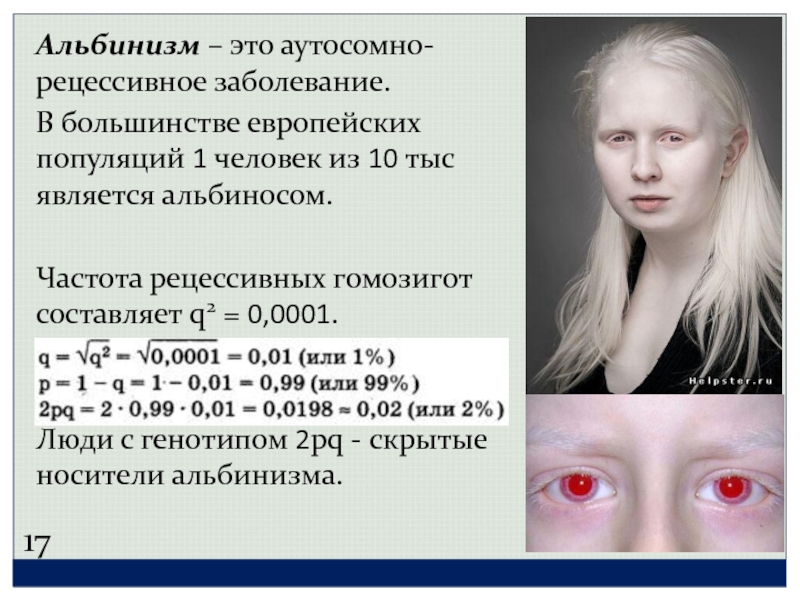
Слайд 18Альбинизм – это аутосомно-рецессивное заболевание.
В большинстве европейских популяций 1 человек
Частота рецессивных гомозигот составляет q2 = 0,0001.
Люди с генотипом 2pq - скрытые носители альбинизма.
17
Слайд 20Заключение.
С помощью формулы Харди-Вайнберга можно определить ожидаемые частоты генотипов и фенотипов
Расчеты показывают, что в последующих поколениях в популяции сохраняется равновесное распределение частот генов.
Правило Харди-Вайнберга указывает на существующие в популяции возможности для ее стабильности, которая нарушается факторами природной среды.
19
Слайд 22Список использованной литературы.
1. Айала Ф., Кайгер Дж. Современная генетика: В 3-х т.
2. География и мониторинг биоразнообразия. Коллектив авторов. М.: Издательство Научного и учебно-методического центра, 2002. – 432 с.
3. Грант Верн. Эволюционный процесс. – М.: Мир, 1989.
4. Равич-Щербо И.В., Марютина Т.М., Григоренко Е.Л. Психогенетика: Уч. Для вузов. – М.: Аспект Пресс, 2000. – 447 с.
5. Словарь терминов по генетике. http://www.glossary.ru
6. Фогель Ф., Мотульски А. Генетика человека: В 3-х т. Т.1: Пер. с англ. – М.: Мир, 1989. – 312 с.
7. Афонин А. А. , Доктор с.-х. наук, профессор Брянского государственного
университета ,Зав. лабораторией популяционной цитогенетики НИИ ФиПИ БГУ
:Общая и теоретическая биология: генетика, эволюция, цитология, экология
учебно-методический комплекс (УМК)
8. Т. Л. Богданова "Пособие для поступающих в вузы"
9. http://bono-esse.ru/blizzard/A/Posobie/Ecol/Genetik/zakon_HV.html
10. http://www.kazedu.kz/referat/141652
11. http://afonin-59-bio.narod.ru/2_heredity/2_heredity_lec/her_lec_11.htm
21















![Презентация к уроку в 10-11 кл. Генетическое равновесие в популяциях Практическое значение закона Харди-Вайнберга.В здравоохранении – позволяет оценить популяционный риск генетических Практическое значение закона Харди-Вайнберга.В здравоохранении – позволяет оценить популяционный риск генетических заболеваний. [17]В селекции – позволяет выявить](/img/thumbs/f6d4c8b0a72b49511aa7d92d2921ed31-800x.jpg)