Презентация, доклад на тему Задачи с параметрами

t2 + (а-1) t+ а-2а2=0 – квадратное уравнение относительно переменной t.
Способ первый. Находим корни квадратного уравнения и определяем, при каких значениях параметра корни положительные.
Имеем: D = (a-1)2 -4(а-2а2) = (3а-1)2, откуда t1 = а , t2 = 1-2а. Для того, чтобы исходное уравнение имело два действительных различных корня, необходимо потребовать от корней квадратного уравнения выполнения условия:

Таким образом, получаем окончательный ответ: при 0 < а < 1/3 или 1/3 < а < ½ уравнение 36х+(а-1)6х+а-2а2=0 имеет два действительных различных корня. Такой способ решения эффективно применять при условии «хорошего» дискриминанта. Рассмотрим другой способ решения задачи 1. А именно, применим теорию расположения корней квадратного трехчлена.

36х+(а-1)6х+а-2а2=0
Пусть 6х = t, где t > 0, тогда уравнение примет вид: t2 + (а-1) t+ а-2а2=0 – квадратное уравнение относительно переменной t.
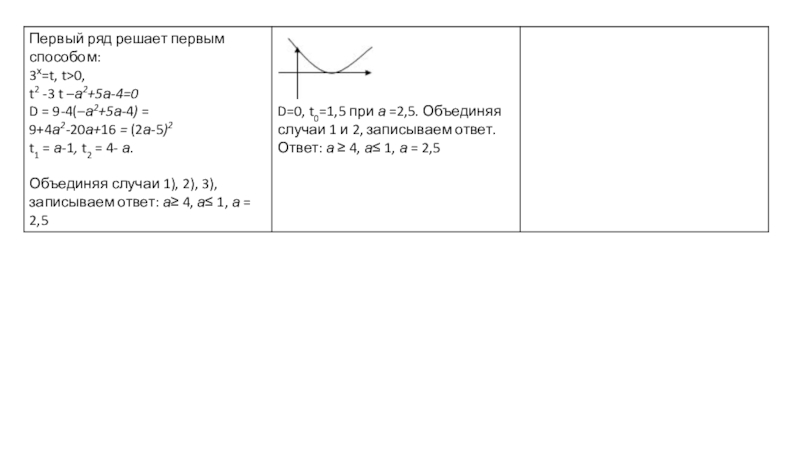
Корни квадратного уравнения t2 + (а-1) t+ а-2а2=0 являются нулями соответствующей квадратичной функции у = t2 + (а-1) t+ а-2а2 . Для того чтобы исходное уравнение имело два различных действительных корня необходимо наличие положительных нулей у функции у = t2 + (а-1) t+ а-2а2. Изобразим геометрическую модель задачи (наличие положительных нулей квадратичной функции)

Теперь осталось «зафиксировать» параболу (ветви направлены вверх, так как первый коэффициент положительный и равен 1) системой алгебраических условий.
Имеем: 1) D > 0 (парабола пересекает ось Оt – условие наличия корней); 2) у(0) > 0 и t0 > 0 (нули функции расположены правее нуля, т. е положительные) Таким образом необходимо решить следующую систему алгебраических неравенств:

Решение системы приводит к ответу: 0 < а < 1/3 или 1/3 < а < ½. Такой способ решения задачи возможен, когда корни квадратного уравнения иррациональны (дискриминант квадратного трехчлена не является
полным квадратом), так как во втором случае мы работаем только с коэффициентами квадратного уравнения.

или

Применение теоремы Виета и ей обратной.
Для того чтобы корни квадратного уравнения имели одинаковые по знаку корни необходимо и достаточно выполнения соотношений

При этом корни будут положительными, если

и отрицательны, если

Кроме этого полезно помнить, что квадратное уравнение имеет корни разных знаков при условии t1 * t2 = с/а < 0 (при этом дискриминант автоматически принимает положительные значения). В нашем случае, исходное уравнение 36х+(а-1)6х+а-2а2=0 имеет два действительных различных корня при условии

Имеем: t2 + (а-1) t+ а-2а2=0 , по теореме Виета (теорема предполагает наличие корней, т.е. D ≥ 0)
t1 * t2 = а-2а2, t1+ t2 = -(а-1). Решая систему неравенств:

приходим к ответу: 0 < а < 1/3 или 1/3 < а < ½.
Легко заметить, что система, составленная с опорой на т. Виета содержит такие же неравенства, как и система, составленная во втором способе решения задачи.

При каких значениях параметра а, уравнение 9х -3x+1 –а2+5а-4=0 имеет единственное решение?

18 — При каких a система неравенств

Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y = |x| – a, причём последний есть график функции y = |x|, сдвинутый вниз на а. Решение данной системы есть пересечение множеств решений каждого из неравенств.
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.

из прямых наклонена к осям под углом 45°. Значит, треугольник PQR – прямоугольный равнобедренный. Точка Q имеет координаты (0, а), а точка R – координаты (0, –а). Кроме того, отрезки PR и PQ равны радиусу окружности, равному 1. Значит,