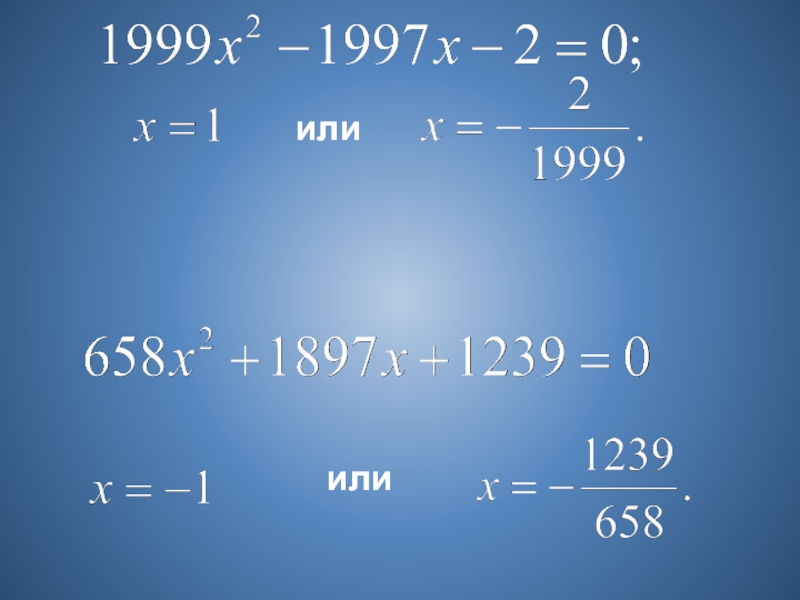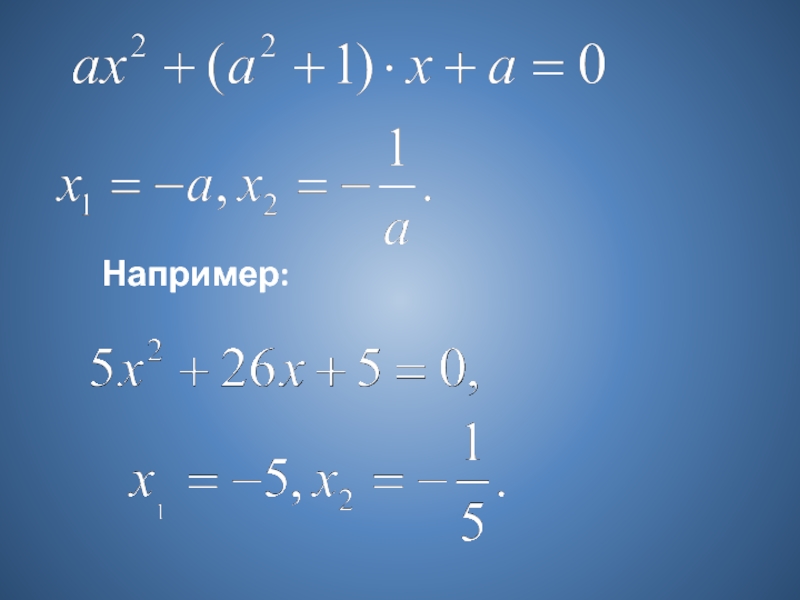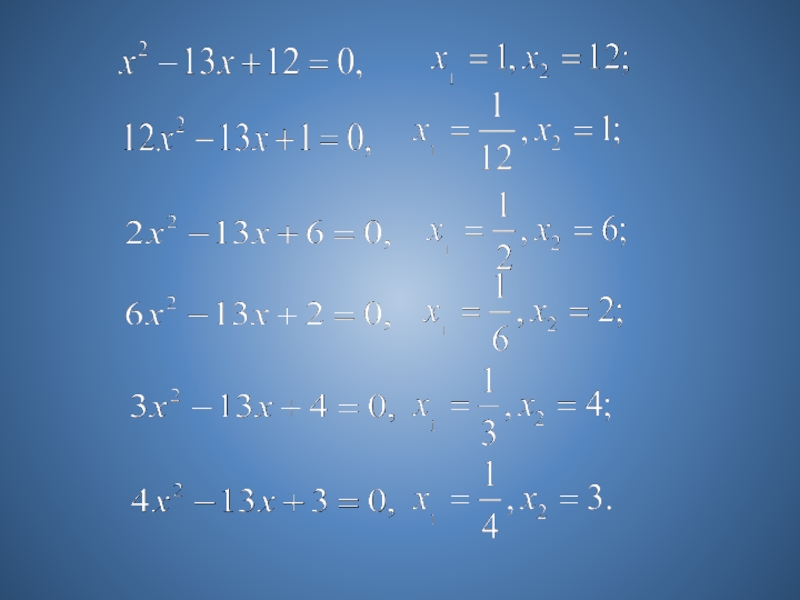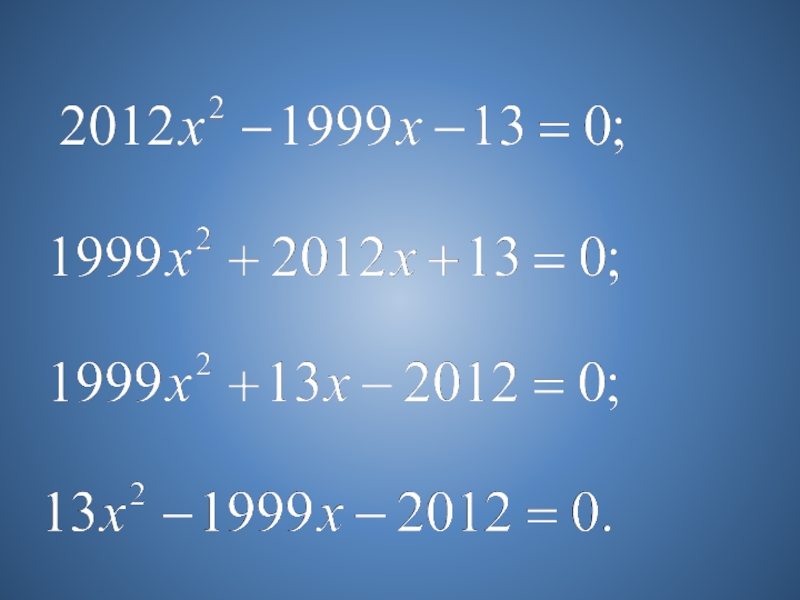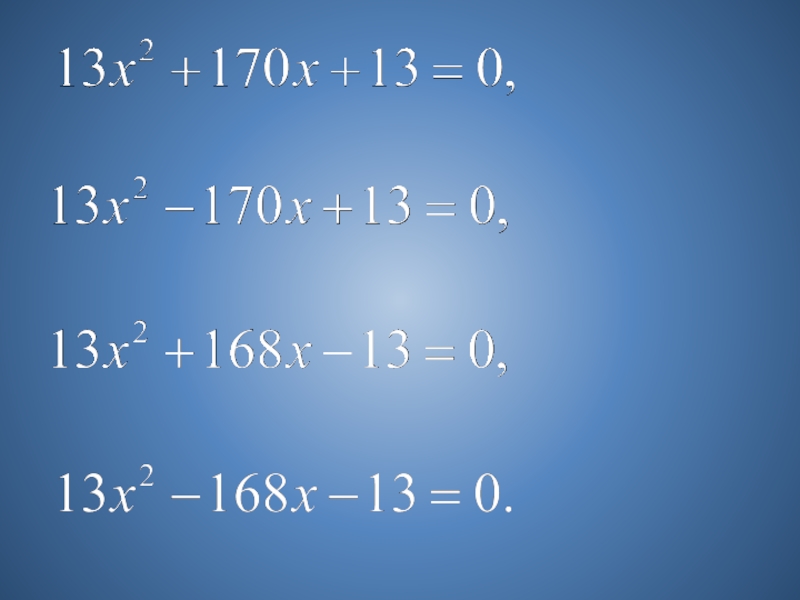- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок-конференция по теме: Методы решения квадратных уравнений
Содержание
- 1. Урок-конференция по теме: Методы решения квадратных уравнений
- 2. «Человеку, изучающему алгебру, часто полезнее решить одну
- 3. Задачи проектаРассмотреть устные способы решения квадратных уравненийИзучить
- 4. В школьном курсе математики изучают
- 5. Уравнение вида
- 6. Из школьного курса нам известны формулы:И теорема
- 7. 1) Если а+в+с=0, то 2) Если а
- 8. Докажем одно из утверждений. Доказательство:В уравнение ах2+вх+с=0
- 9. Используя новые устные приемы , можно решать уравнения легко и просто!
- 10. илиили
- 11. Уравнение вида:имеет корни:
- 12. Доказательство:По формуле I найдем:
- 13. Например:
- 14. Уравнение вида:имеет корни:Например:
- 15. Уравнение вида:имеет корни:Например:
- 16. Уравнение вида:имеет корни:Например:
- 17. Но это еще не все открытия ,
- 18. Замечаем, что при переброске одного из
- 19. Например: уравнение имеет корни так как а+в+с=0,
- 20. Используя рассмотренные приемы, можно придумывать уравнения с
- 21. Слайд 21
- 22. корнями которого будут числа 1 и 20.
- 23. Проверь себя!
- 24. Слайд 24
- 25. Слайд 25
- 26. Источник знанийЭнциклопедический словарь юного математикаЖурнал «Математика в
- 27. Спасибоза внимание
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается
Слайд 2«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу
тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
Уолтер Варвик Сойер
Уолтер Варвик Сойер
Слайд 3Задачи проекта
Рассмотреть устные способы решения квадратных уравнений
Изучить теоретический материал по данной
теме
Выделить различные способы решения уравнений
Показать применение данных способов при решении уравнений с большими коэффициентами
Подобрать тренировочные задания для отработки изученных приемов
Научиться устно решать квадратные уравнения
Выделить различные способы решения уравнений
Показать применение данных способов при решении уравнений с большими коэффициентами
Подобрать тренировочные задания для отработки изученных приемов
Научиться устно решать квадратные уравнения
Слайд 4 В школьном курсе математики изучают формулы корней квадратных уравнений,
с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Разберём некоторые из них.
Слайд 5Уравнение вида
где -переменная,
- некоторые числа,
, называется квадратным уравнением.
Примеры:
Примеры:
Слайд 6Из школьного курса нам известны формулы:
И теорема обратная теореме Виета, которая
позволяет устно подбирать корни приведенного квадратного уравнения:
Если числа m и n таковы, что m+n=-p, а mn=q, то:
Слайд 71) Если а+в+с=0, то
2) Если а + с = в,
то
Мы заметили, что
Назвали это:
Приёмом «Коэффициентов»:
Слайд 8Докажем одно из утверждений. Доказательство:
В уравнение ах2+вх+с=0 подставим
в = а
+ с, получим
ах2+(а + с)х+с=0 , преобразуем:
(ах2+ах) + (сх+с)=0 ,
ах(х+1)+с(х+1)=0,
(х+1)(ах+с)=0,
х+1=0 или ах+с=0,
откуда х=-1 или х=-с/а.
ах2+(а + с)х+с=0 , преобразуем:
(ах2+ах) + (сх+с)=0 ,
ах(х+1)+с(х+1)=0,
(х+1)(ах+с)=0,
х+1=0 или ах+с=0,
откуда х=-1 или х=-с/а.
Слайд 17Но это еще не все открытия , связанные с коэффициентами квадратного
уравнения. Пусть в уравнении
свободный член c = m·n.
Тогда его можно записать в виде :
(1)
Сравним корни уравнения (1) с корнями уравнения
(2).
Слайд 18 Замечаем, что при переброске одного из множителей свободного члена к
старшему коэффициенту дискриминант не изменяется,
то есть
Корни уравнения (1) вычисляются по формуле
а уравнения (2) по формуле:
Делаем вывод, что корни уравнения (2) получаются делением корней уравнения (1) на переброшенный множитель.
Слайд 19Например:
уравнение
имеет корни
так как а+в+с=0, а значит уравнение
имеет
корни .
Уравнение
имеет корни
Слайд 20Используя рассмотренные приемы, можно придумывать уравнения с рациональными корнями.
Свободный член
12 делится на 1,2,3,4,6 и 12. Отсюда уравнения:
Например, возьмем уравнение:
корни которого мы уже
нашли : 1 и 12.
Слайд 22корнями которого будут числа 1 и 20.
Решим уравнение:
Разделим найденные
корни на старший коэффициент число 4, получим корни исходного уравнения (1) :
Получим уравнение:
переброска
Слайд 26Источник знаний
Энциклопедический словарь юного математика
Журнал «Математика в школе»№6 2008 год
Садыхов С.Н.,
Попов В.В. Развитие творческой активности учащихся в процессе решения заданий с использованием устных приемов решения квадратных уравнений. М.: НИИ школ, 2004.
