- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Учебная презентация по теме Квадратный трёхчлен
Содержание
- 1. Учебная презентация по теме Квадратный трёхчлен
- 2. I. Повторениеx -10 -8
- 3. 2. Решите уравнение х3 – 6х2
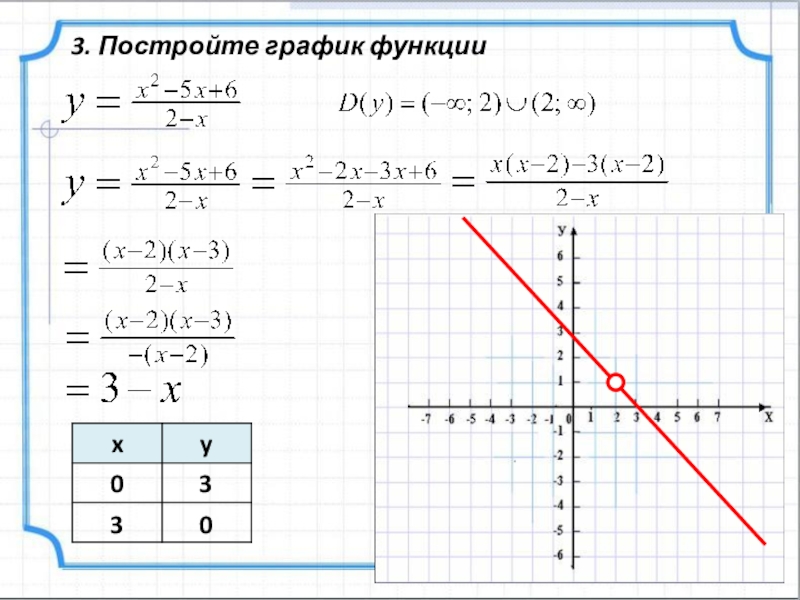
- 4. 3. Постройте график функции0330
- 5. II. ОпределениеКвадратный трехчлен (КТ) –Многочлен вида ах2
- 6. Задача №1Найдите корни квадратного трёхчлена 3х2 –
- 7. III. Выделение квадрата двучлена из КТПредставление КТ
- 8. Задача №3Докажите, что из всех прямоугольников с
- 9. Классная работа:№ 64 (а, в)№ 65 (а, в)№ 66 (а, в)№ 68
- 10. IV. Разложение КТ на множителиЧто называют разложением
- 11. Теорема 1.Если х1 и х2 - корни
- 12. Теорема 2.Если квадратный трехчлен не имеет корней,
- 13. Задача №5Разложите на множители КТ 2х2 +
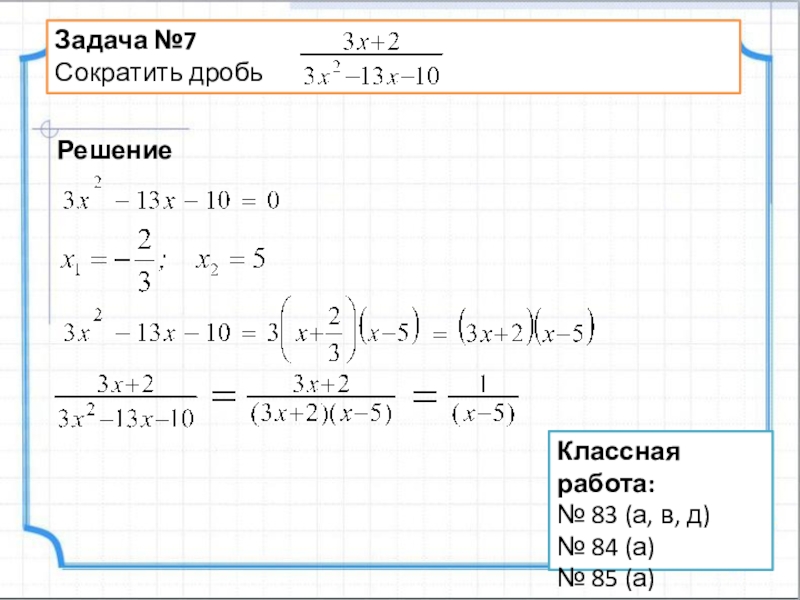
- 14. Задача №7Сократить дробьРешениеКлассная работа:№ 83 (а, в, д)№ 84 (а)№ 85 (а)
- 15. Домашнее задание§2, п.3, п.4№ 56 (б, г),
Слайд 1Задача, которую вы решаете, может быть очень скромной, но если она
Слайд 2I. Повторение
x
-10 -8 -6
8
6
4
2
-2
-4
-6
Область определения
D(f)=[- 8; 6]
Значение функции
при значении аргумента равного 2
Значение аргумента,
при котором значение функции равно - 3
Нули функции
Промежутки знакопостоянства
Промежутки возрастания и убывания
Область значений
Е(f)=[-5; 4]
Слайд 32. Решите уравнение х3 – 6х2 – 4х + 24 =
Решение:
(х3 – 6х2 ) – (4х – 24 ) = 0;
х2(х – 6 ) – 4(х – 6 ) = 0;
(х2 – 4 ) (х – 6 ) = 0;
х2 – 4 = 0 или х – 6 = 0;
Ответ: -2; 2; 6
Слайд 5II. Определение
Квадратный трехчлен (КТ) –
Многочлен вида ах2 + bх + c,
Корень многочлена –
Значение переменной, при котором многочлен обращается в нуль.
Найти корни КТ ах2 + bх + c
Решить квадратное уравнение ах2 + bх + c = 0
D = b2 – 4ac – дискриминант КТ
D > 0 –КТ имеет два корня
D = 0 –КТ имеет один корень
D < 0 –КТ не имеет корней
Слайд 6Задача №1
Найдите корни квадратного трёхчлена 3х2 – 2х – 5.
Решение
Ответ:
Классная работа:
№
№ 59 (а, в, д)
№ 60 (а, в)
Слайд 7III. Выделение квадрата двучлена из КТ
Представление КТ ах2 + bх +
Задача №2
Выделите из трёхчлена 3х2 – 36х + 140 квадрат двучлена.
Слайд 8Задача №3
Докажите, что из всех прямоугольников с периметром 20 см наибольшую
X см
10 – Х см
Выделим квадрат двучлена
a = -1, b = 10, c = 0
Все стороны по 5 см прямоугольник квадрат
ЧТД
Слайд 10IV. Разложение КТ на множители
Что называют разложением многочлена на множители?
Представление
Какие способы разложения многочлена на множители вам известны?
Вынесение множителя за скобку
Способ группировки
Использование формул сокращенного умножения
Задача №4. Разложить на множители 3х2 – 21х + 30
Решение:
3х2 – 21х + 30 = 3(х2 – 7х + 10) = 3(х2 – 2х – 5х + 10) =
3((х2 – 2х) – (5х – 10)) = 3(х(х – 2) – 5(х – 2)) = 3(х – 2)(х – 5)
Гипотеза: ах2 + bx + c = а(х – х1)(х – х2)
Слайд 11Теорема 1.
Если х1 и х2 - корни квадратного трехчлена ах2 +
Доказательство
(Теорема Виета)
ЧТД
Слайд 12Теорема 2.
Если квадратный трехчлен не имеет корней, то его нельзя разложить
Доказательство (метод от противного)
Пусть КТ можно представить в виде произведения многочленов 1-ой степени:
ах2 + bx + c = (kx + m)(px + q)
где k, m, p, q – некоторые числа, k 0 и p 0.
Найдем корни многочлена:
(kx + m)(px + q)= 0
Противоречие:
По условию этот трехчлен корней не имеет.
ЧТД
Слайд 13Задача №5
Разложите на множители КТ 2х2 + 7х – 4
Решение
2х2 +
x1 = ½; x2 = -4
2х2 + 7х – 4 = 2(x – ½)(x + 4)
= (2x – 1)(x + 4)
Задача №6
Разложите на множители -4х2 + 24х – 36
Решение
-4х2 + 24х – 36
x1 = x2 = 3
-4х2 + 24х – 36 = -4(x – 3)(x – 3) = -4(x – 3)2
Классная работа:
№ 76 (а, в, д, ж, и)
№ 77 (а, в)
№ 78 (а, в)
Слайд 15Домашнее задание
§2, п.3, п.4
№ 56 (б, г), № 59 (б, г,
№ 64 (б, г), № 65 (б, г), № 66 (б, г), № 69
№ 76 (б, г, е, з), № 77 (б, г), № 78 (б, г)
№ 83 (б, г, е), № 84 (б), № 85 (б)