- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тригонометрические функции
Содержание
- 1. Тригонометрические функции
- 2. Цель : знакомство с тригонометрическими функциями; формирование
- 3. Тема 1. Синус и косинус. Тангенс и
- 4. Отношение синуса угла α к косинусу того
- 5. Свойства синуса, косинуса, тангенса и котангенса:Свойство 1.
- 6. Свойство 3. Для любого значения t справедливы равенства:sin(t+π) =
- 7. Геометрическая иллюстрация для тангенса и котангенса.Проведём в
- 8. Аналогично можно ввести линию котангенсов — числовая прямая m с началом в точке B
- 9. Слайд 9
- 10. Тема 2. Тригонометрические функции на единичной окружности.
- 11. Важно уметь считывать с круга следующие значения синуса и косинуса:tg 0∘=0; tg 90∘ не существует;tg 180∘=0; tg 270∘ не существует;tg 360∘=0 ctg 0∘ не существует;ctg 90∘=0; ctg 180∘ не существует;ctg 270∘=0; ctg 360∘ не существует
- 12. Контрольные вопросы:Дать определение синуса.Дать определение косинуса.Дать определение тангенса.Дать определение котангенса.Назовите основные свойства тригонометрических функций.
Слайд 2Цель : знакомство с тригонометрическими функциями; формирование знаний и умений в
Задачи
1. Образовательные:
- дать определения тригонометрическим функциям;
рассмотреть основные свойства тригонометрических функций;
2. Развивающие:
- способствовать развитию умений анализировать, устанавливать связи, причины и следствия;
- предвидеть возможные ошибки и способы их устранения;
- способствовать повышению концентрации внимания, развитию памяти и речи.
3. Воспитательные:
- способствовать развитию интереса к предмету «Математика»
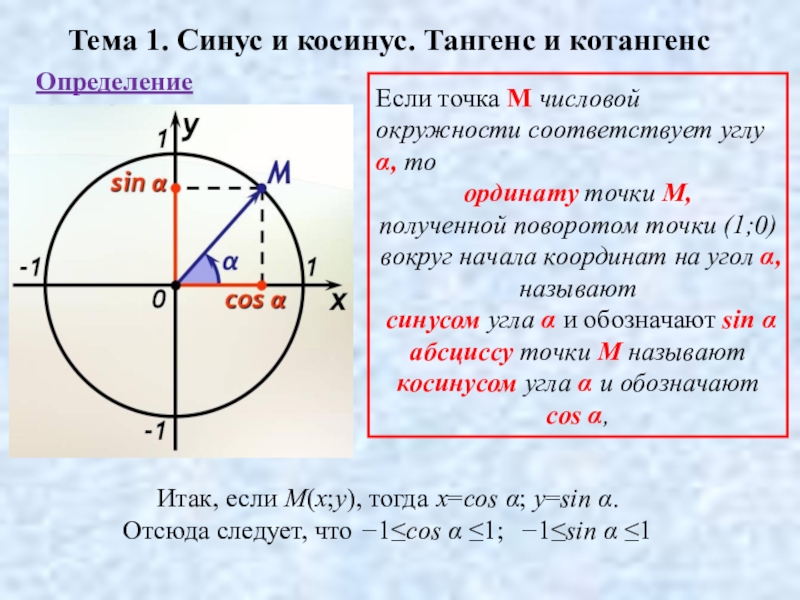
Слайд 3Тема 1. Синус и косинус. Тангенс и котангенс
Если точка M
ординату точки M,
полученной поворотом точки (1;0) вокруг начала координат на угол α, называют
синусом угла α и обозначают sin α
абсциссу точки M называют
косинусом угла α и обозначают cos α,
Итак, если M(x;y), тогда x=cos α; y=sin α.
Отсюда следует, что −1≤cos α ≤1; −1≤sin α ≤1
Определение
Слайд 4Отношение синуса угла α к косинусу того же угла называют тангенсом
Отношение косинуса угла α к синусу того же угла называют котангенсом угла α и обозначают ctg α.
Определение
Получим, что:
Из уравнения числовой окружности x2+y2=1, заменяя x и y на cos α и sin α, получаем равенство
cos2 α +sin2 α =1.
Слайд 5Свойства синуса, косинуса, тангенса и котангенса:
Свойство 1. Для любого значения t справедливы равенства:
sin(−t)
cos(−t) = cost;
tg(−t) = −tgt;
ctg(−t) = −ctgt.
Свойство 2. Для любого значения t справедливы равенства:
sin(t+2πn) = sint;
cos(t+2πn) = cost.
Слайд 6Свойство 3. Для любого значения t справедливы равенства:
sin(t+π) = −sint;
cos(t+π) = −cost;
tg(t+π) =
ctg(t+π) = ctgt.
Будут верны и такие равенства:
tg(t+πn) = tgt;
ctg(t+πn) = ctgt.
Свойство 4. Для любого значения t справедливы равенства:
sin(t+π/2) = cost;
cos(t+π/2) =−sint.
Слайд 7Геометрическая иллюстрация для тангенса и котангенса.
Проведём в координатной плоскости к числовой
Эту касательную L будем считать числовой прямой, ориентированной так же, как ось y, и с началом в точке A
Из подобия ∆ OMK и ∆ OPA следует равенство:
Т. е. PA=tg t
Числовую прямую L называют линией тангенсов.
Итак, если числу t соответствует на числовой окружности точка M, то, проведя прямую OM,
получим в пересечении её с числовой прямой L, точку P, которая имеет на числовой прямой L координату tg t.
L
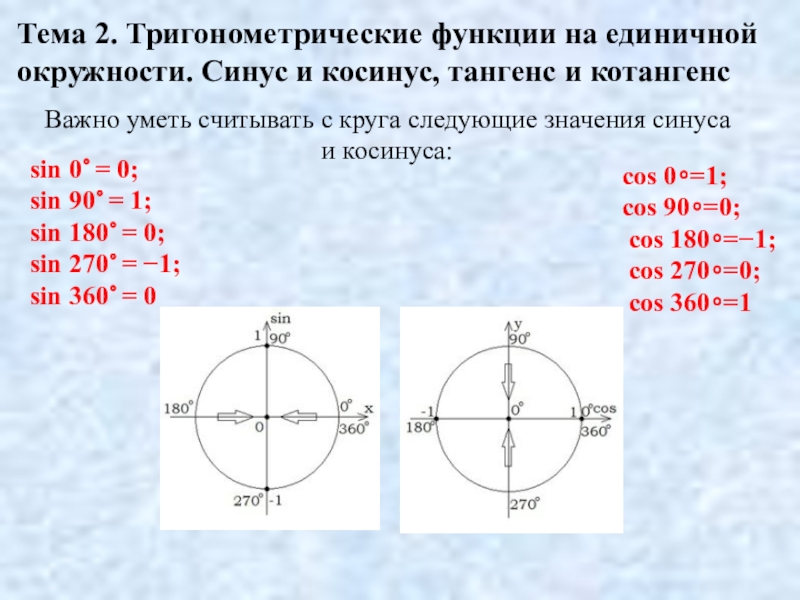
Слайд 10Тема 2. Тригонометрические функции на единичной окружности. Синус и косинус, тангенс
sin 0∘ = 0;
sin 90∘ = 1;
sin 180∘ = 0;
sin 270∘ = −1;
sin 360∘ = 0
Важно уметь считывать с круга следующие значения синуса и косинуса:
cos 0∘=1;
cos 90∘=0;
cos 180∘=−1;
cos 270∘=0;
cos 360∘=1
Слайд 11Важно уметь считывать с круга следующие значения синуса и косинуса:
tg 0∘=0;
tg 90∘ не
tg 180∘=0;
tg 270∘ не существует;
tg 360∘=0
ctg 0∘ не существует;
ctg 90∘=0;
ctg 180∘ не существует;
ctg 270∘=0;
ctg 360∘ не существует
Слайд 12Контрольные вопросы:
Дать определение синуса.
Дать определение косинуса.
Дать определение тангенса.
Дать определение котангенса.
Назовите основные
