- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Свойства функции синус и её график.
Содержание
- 1. Презентация. Свойства функции синус и её график.
- 2. Свойства функции1.D(y)2.E(y)3. Четность функции4. Периодичность функции5.Нули функции6.
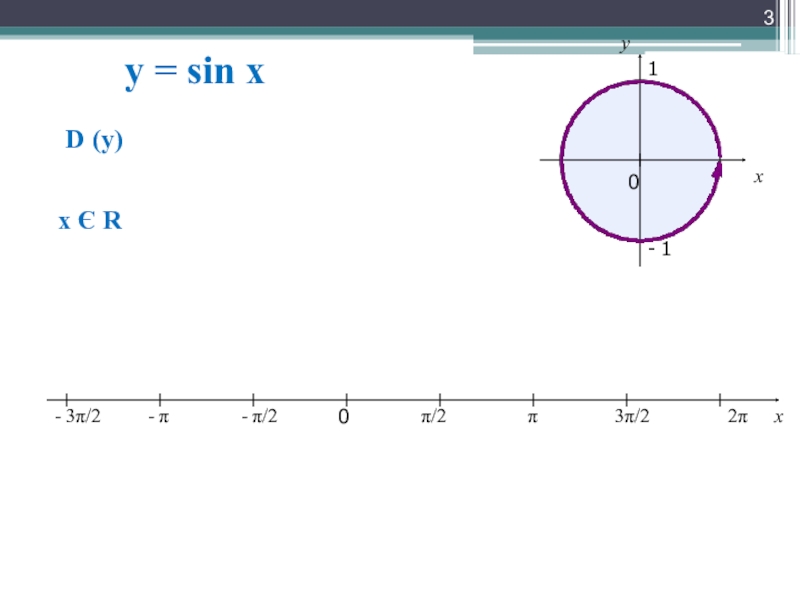
- 3. y = sin xx0π/2π3π/22π- π/2- π- 3π/2 D (y)x Є R
- 4. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/21- 10 E (y)[ -1; 1]
- 5. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π-
- 6. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/21- 10 Периодичность функцииПериод функции Т=2π,sin(x+2π)=sin x
- 7. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π-
- 8. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π-
- 9. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π-
- 10. y = sin на отрезке xy0π/2π3π/22πxy1- 1-
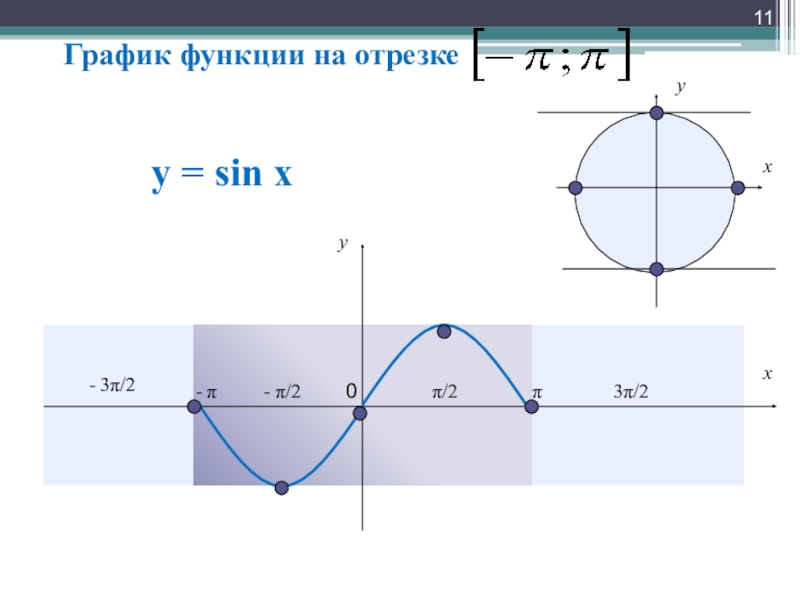
- 11. у = sin x ππ/2- π/2- π- 3π/23π/2yx0yxГрафик функции на отрезке
- 12. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/2
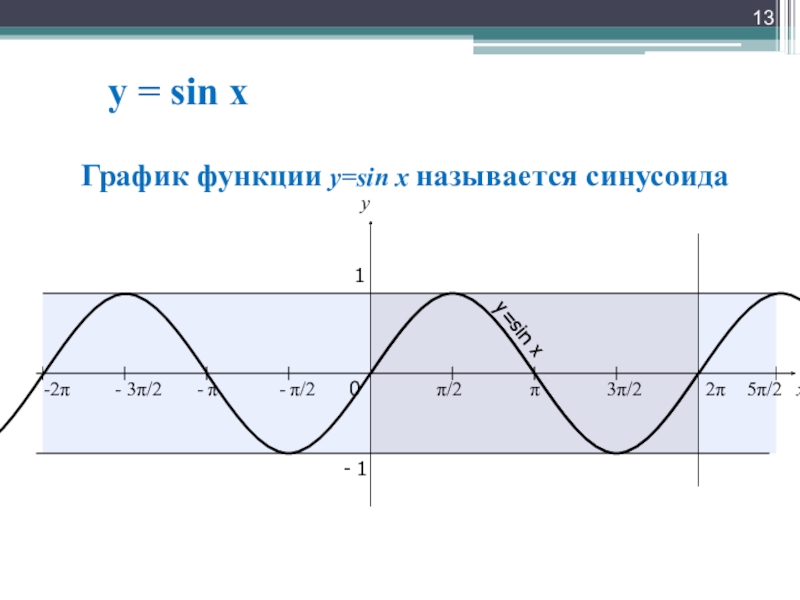
- 13. y = sin xxy0π/2π3π/22π1- 1- π/2- π- 3π/2-2π5π/2y=sin xГрафик функции y=sin x называется синусоида
- 14. y = sin x++xy0π/2π3π/22πxy1- 1 Положительные значения
- 15. y = sin x––xy0π/2π3π/22πxy1- 1 Отрицательные значения sin x
- 16. y = sin xxy0π/2π3π/22πxy1- 1 Функция возрастает- π/2- π- 3π/2на отрезке [-π/2+2πk; π/2+2πk]Промежутки возрастания
- 17. y = sin xxy0π/2π3π/22πxy1- 1 Функция убывает- π/2- π- 3π/2на отрезке [π/2+2πk; 3π/2+2πk]Промежутки убывания
- 18. Сравнить числа sin 2
- 19. УпражненияПользуясь свойствами функции у = sin x
- 20. Расположить в порядке возрастания числа sin 1.9
- 21. Используя свойство возрастания или убывания функции y=sinx, сравните числа:ииии1 вариант2 вариант
- 22. Разбить отрезок
- 23. № 722 Разбить данный отрезок на
- 24. Сдвиг вдоль оси ординат Построить график функции
- 25. Сдвиг вдоль оси абсциссПостроить график функции у=sin(х
- 26. Сжатие и растяжение к оси абсциссK >
- 27. Сжатие и растяжение к оси ординатПостроить график
- 28. Ухy = sin xПри каких значениях х
Слайд 2Свойства функции
1.D(y)
2.E(y)
3. Четность функции
4. Периодичность функции
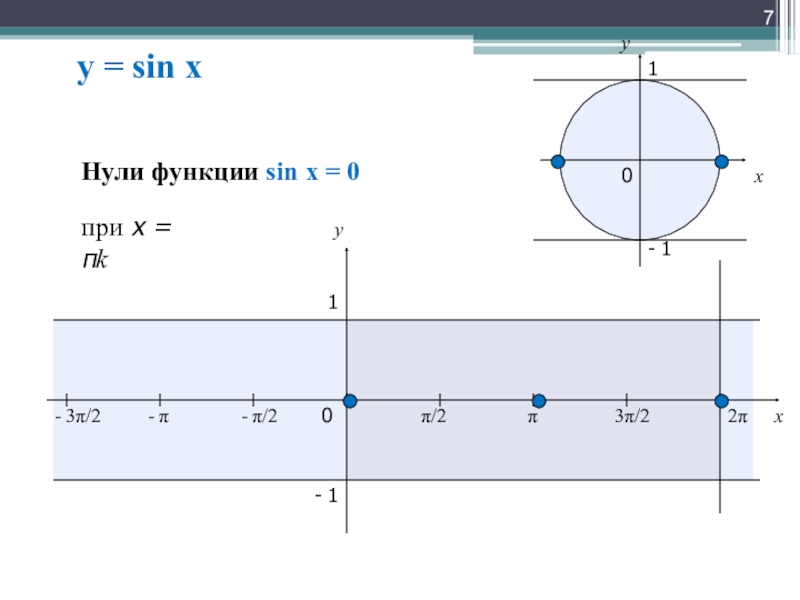
5.Нули функции
6. Наибольшее значение
7. Наименьшее значение
8.
9. Отрицательные значения
10. Возрастание функции
11. Убывание функции
Слайд 5y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
- π/2
- π
- 3π/2
1
- 1
0
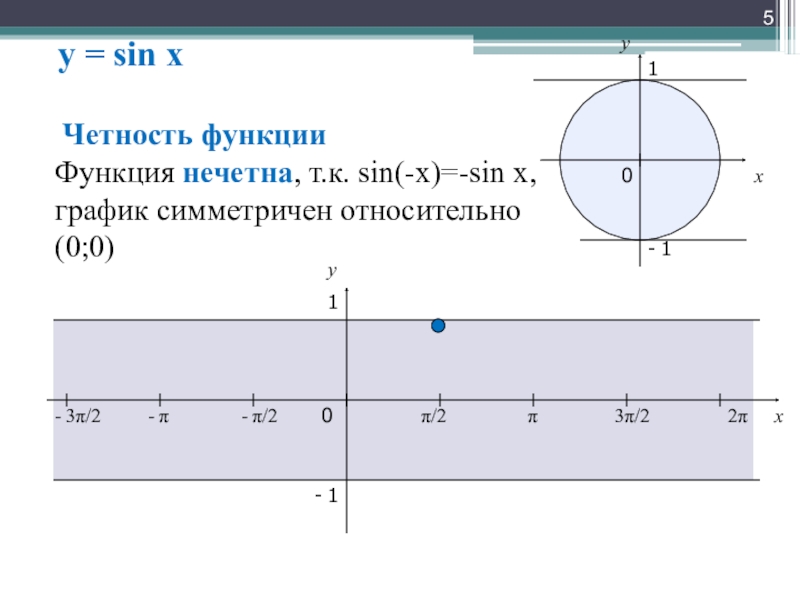
Четность функции
Функция
график симметричен относительно (0;0)
Слайд 6y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
- π/2
- π
- 3π/2
1
- 1
0
Периодичность функции
Период
sin(x+2π)=sin x
Слайд 8y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
- π/2
- π
- 3π/2
1
- 1
0
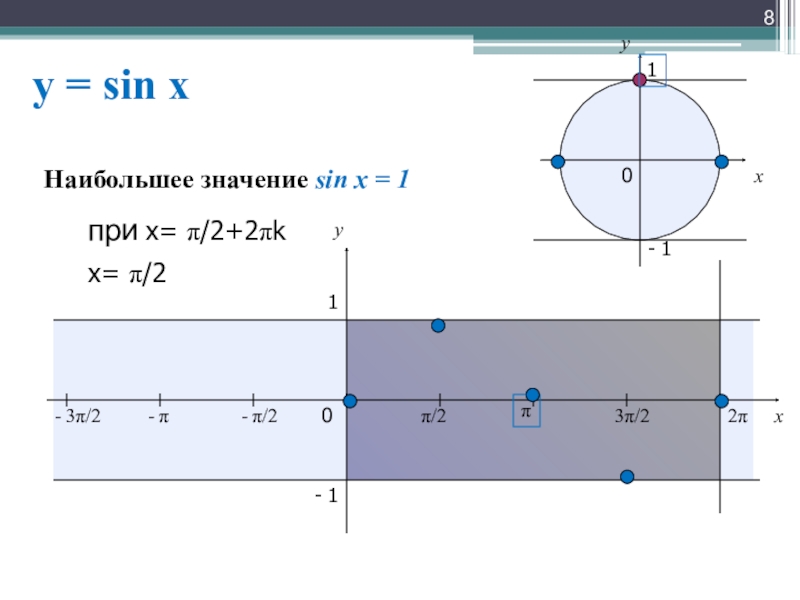
Наибольшее значение
при х= π/2+2πk
х= π/2
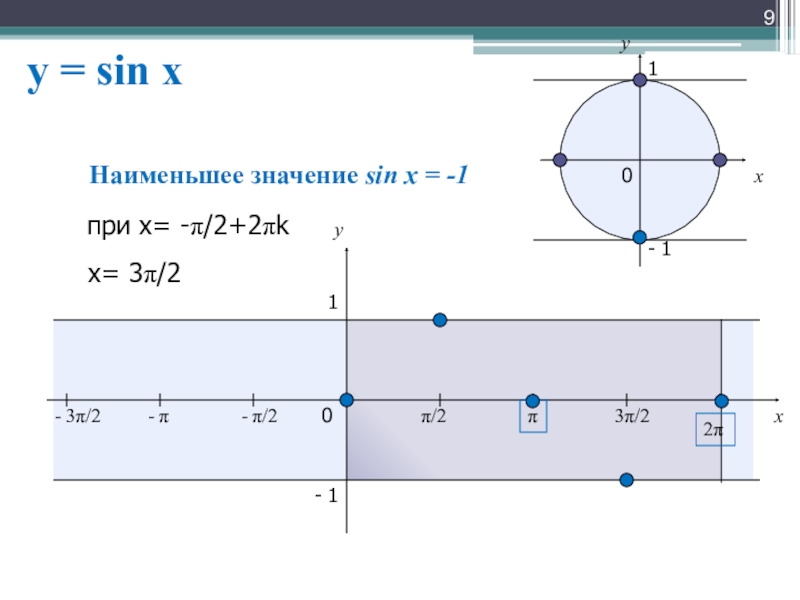
Слайд 9y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
- π/2
- π
- 3π/2
1
- 1
0
Наименьшее значение
при х= -π/2+2πk
х= 3π/2
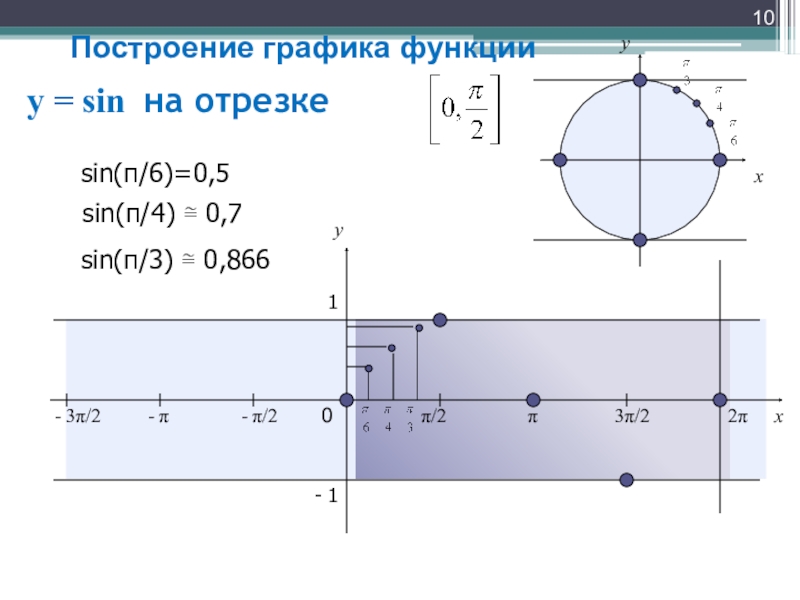
Слайд 10y = sin на отрезке
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
- π/2
- π
- 3π/2
sin(π/6)=0,5
sin(π/4)
sin(π/3) ≅ 0,866
Построение графика функции
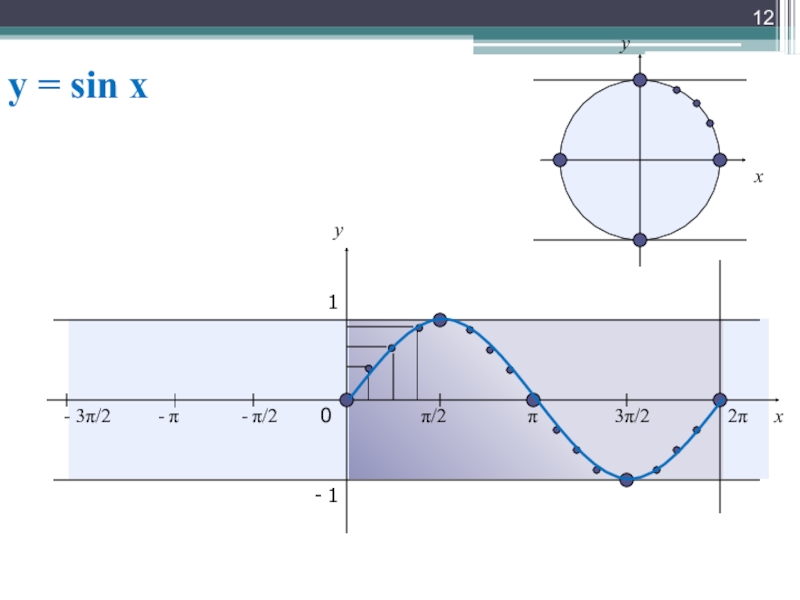
Слайд 13y = sin x
x
y
0
π/2
π
3π/2
2π
1
- 1
- π/2
- π
- 3π/2
-2π
5π/2
y=sin x
График функции y=sin
Слайд 14y = sin x
+
+
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
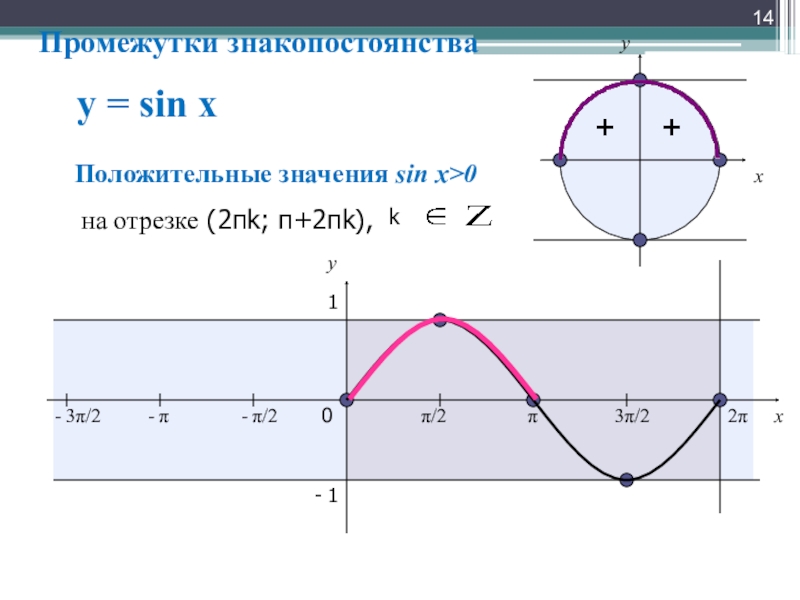
Положительные значения sin x>0
- π/2
- π
-
на отрезке (2πk; π+2πk),
Промежутки знакопостоянства
k
k
Слайд 15y = sin x
–
–
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
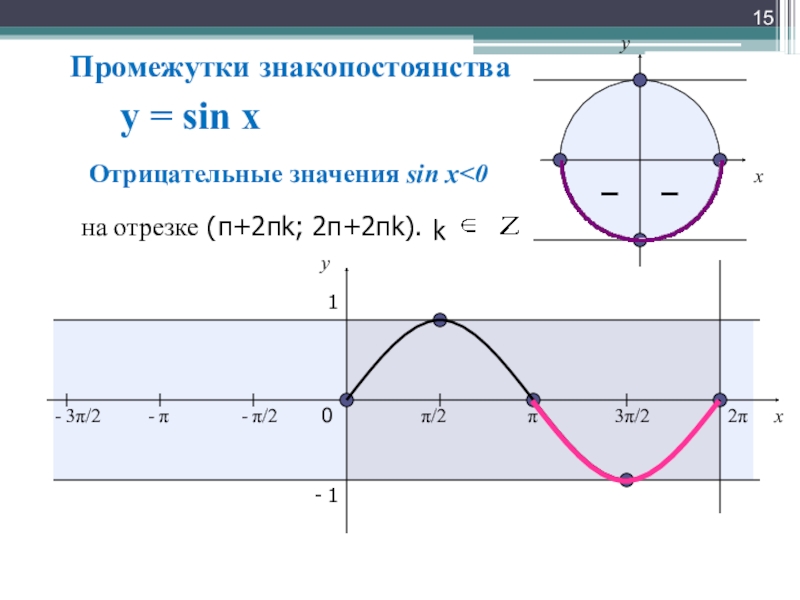
Отрицательные значения sin x
на отрезке (π+2πk; 2π+2πk).
Промежутки знакопостоянства
.
k
Слайд 16y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
Функция возрастает
- π/2
- π
- 3π/2
на отрезке
Промежутки возрастания
Слайд 17y = sin x
x
y
0
π/2
π
3π/2
2π
x
y
1
- 1
Функция убывает
- π/2
- π
- 3π/2
на отрезке
Промежутки убывания
Слайд 18Сравнить числа sin 2 и
Задача
Так как = 3,14, , то
< 2 < 3 <
Из графика видно, что на отрезке функция у=sinх убывает.
Ответ: sin 2 > sin 3.
Слайд 19Упражнения
Пользуясь свойствами функции у = sin x , сравните числа:
sin 4 и sin 2
и
Слайд 20Расположить в порядке возрастания числа sin 1.9 ; sin 3;
Числа sin 1.9 и sin 3 положительны, так как точки Р1,9 и Р3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9
Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти.
Функция у=sinх во 4 четверти возрастает..
sin(-1.5) < sin(-1.5)
Ответ:
Таким образом, в порядке возрастания эти чила располагаются так:
sin(-1.5); sin(-1); sin 3; sin 1.9.
Слайд 21Используя свойство возрастания или убывания функции y=sinx, сравните числа:
и
и
и
и
1 вариант
2 вариант
Слайд 22Разбить отрезок
Ответ; На отрезке функция у=sin х убывает,
а на отрезке функция возрастает.
Слайд 23№ 722 Разбить данный отрезок на два отрезка так, чтобы
1)
- Функция возрастает
- Функция убывает
2)
- Функция убывает
- Функция возрастает
3)
- Функция убывает
- Функция возрастает
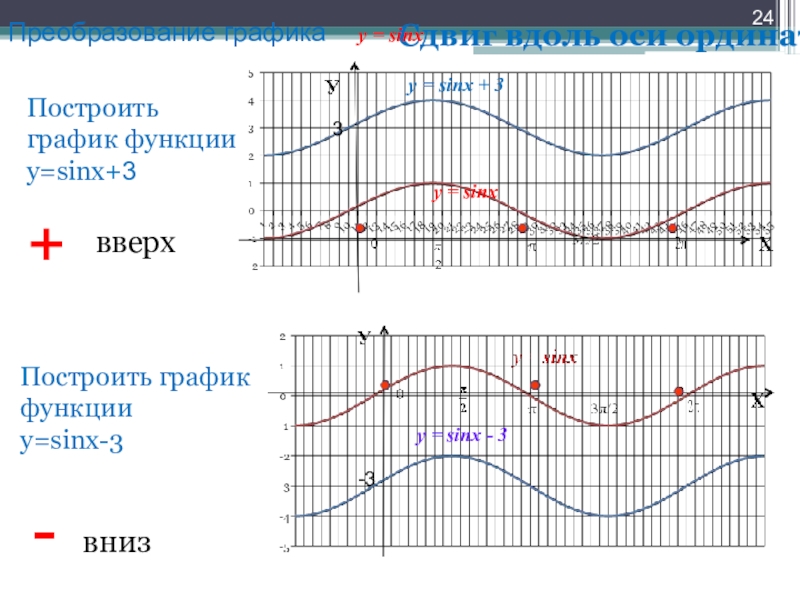
Слайд 24Сдвиг вдоль оси ординат
Построить график функции
Построить график функции у=sinх-3
+
вверх
-
вниз
y = sinx
y = sinx + 3
y = sinx
y = sinx - 3
3
-3
Преобразование графика
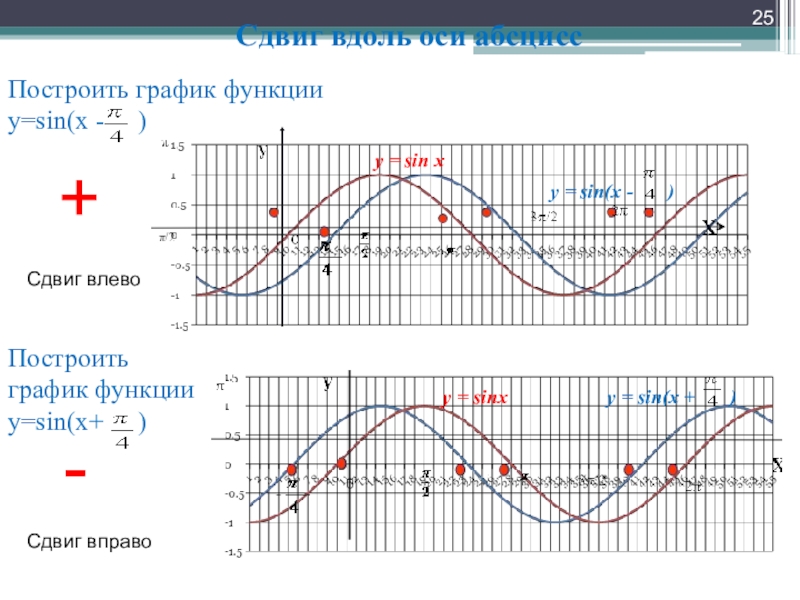
Слайд 25Сдвиг вдоль оси абсцисс
Построить график функции у=sin(х - )
Построить
+
Сдвиг влево
-
Сдвиг вправо
y = sin x
y = sin(x - )
y = sin(x + )
y = sinx
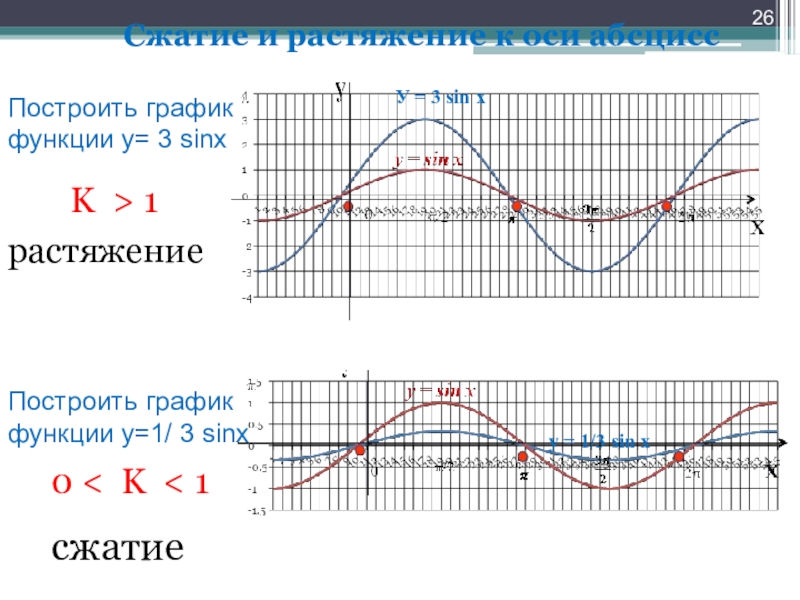
Слайд 26Сжатие и растяжение к оси абсцисс
K > 1
растяжение
0
сжатие
Построить график функции у= 3 sinх
Построить график функции у=1/ 3 sinх
У = 3 sin x
у = 1/3 sin x
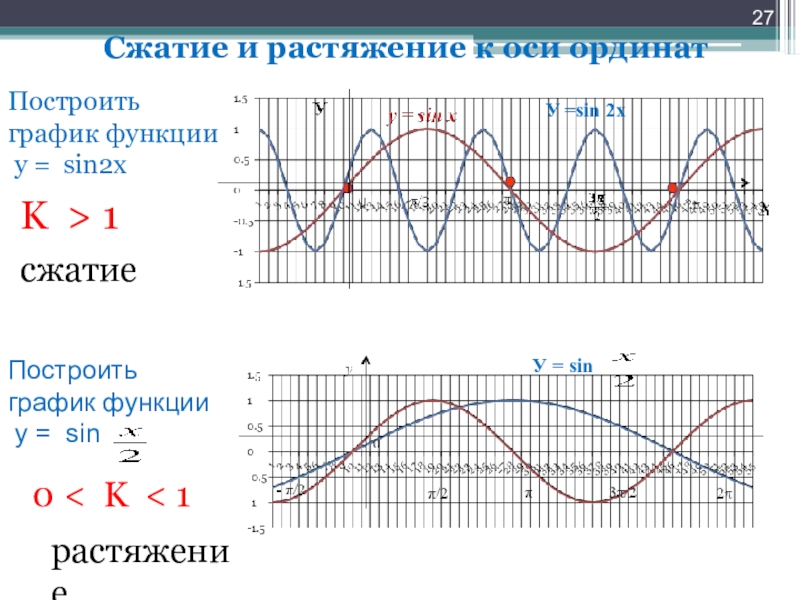
Слайд 27Сжатие и растяжение к оси ординат
Построить график функции
у = sin2х
Построить
у = sin
K > 1
сжатие
0 < K < 1
растяжение
У =sin 2х
У = sin
Слайд 28
У
х
y = sin x
При каких значениях х функция у=sinx принимает значение,
Может ли функция у=sinx принимать значение больше 1, меньше -1?
При каких значениях х функция у=sinx принимает наибольшее (наименьшее) значение?
Каково множество значений функции у=sinx?


![Презентация. Свойства функции синус и её график. y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/21- 10 E (y)[ -1; 1] y = sin xxy0π/2π3π/22πxy1- 1- π/2- π- 3π/21- 10 E (y)[ -1; 1]](/img/thumbs/b521935ca64dcab16f1c175e91d3bc16-800x.jpg)

![Презентация. Свойства функции синус и её график. y = sin xxy0π/2π3π/22πxy1- 1 Функция возрастает- π/2- π- 3π/2на отрезке [-π/2+2πk; π/2+2πk]Промежутки возрастания y = sin xxy0π/2π3π/22πxy1- 1 Функция возрастает- π/2- π- 3π/2на отрезке [-π/2+2πk; π/2+2πk]Промежутки возрастания](/img/thumbs/4a9e3a0727dae802146ae1f1f29455ea-800x.jpg)
![Презентация. Свойства функции синус и её график. y = sin xxy0π/2π3π/22πxy1- 1 Функция убывает- π/2- π- 3π/2на отрезке [π/2+2πk; 3π/2+2πk]Промежутки убывания y = sin xxy0π/2π3π/22πxy1- 1 Функция убывает- π/2- π- 3π/2на отрезке [π/2+2πk; 3π/2+2πk]Промежутки убывания](/img/thumbs/b1bd9bb17a1287f1cc2831642aaa277f-800x.jpg)