г.Ульяновска
Махмутовой Татьяны
Руководитель:
Гульнова И.Ю.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии по теме Движения
Содержание
- 1. Презентация по геометрии по теме Движения
- 2. Понятие движенияДвижение плоскости – это отображение плоскости
- 3. Осевая симметрияОсевая симметрия представляет собой отображение плоскости
- 4. Фигура называется симметричной относительно прямой а, если
- 5. Центральная симметрияЦентральная симметрия с центром в точке
- 6. Однако можно заметить, что центральная симметрия является
- 7. Буквы А, М, Т, Ш, Е имеют
- 8. Параллельный переносПараллельный переносом называют преобразование плоскости ,
- 9. Название «параллельный перенос» оправдывается тем, что при
- 10. ПоворотПоворотом на плоскости около данной точки называется
- 11. Слайд 11
Понятие движенияДвижение плоскости – это отображение плоскости на себя , сохраняющее расстояния .Примером движения могут служить :-осевая симметрия;-центральная симметрия;-параллельный перенос;-поворот.
Слайд 2Понятие движения
Движение плоскости – это отображение плоскости на себя , сохраняющее
расстояния .
Примером движения могут служить :
-осевая симметрия;
-центральная симметрия;
-параллельный перенос;
-поворот.
Слайд 3Осевая симметрия
Осевая симметрия представляет собой отображение плоскости на себя, которое сохраняет
расстояние между точками.
А
А1
В В1
С С1
а
Слайд 4Фигура называется симметричной относительно прямой а, если для каждой точки фигуры
симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.
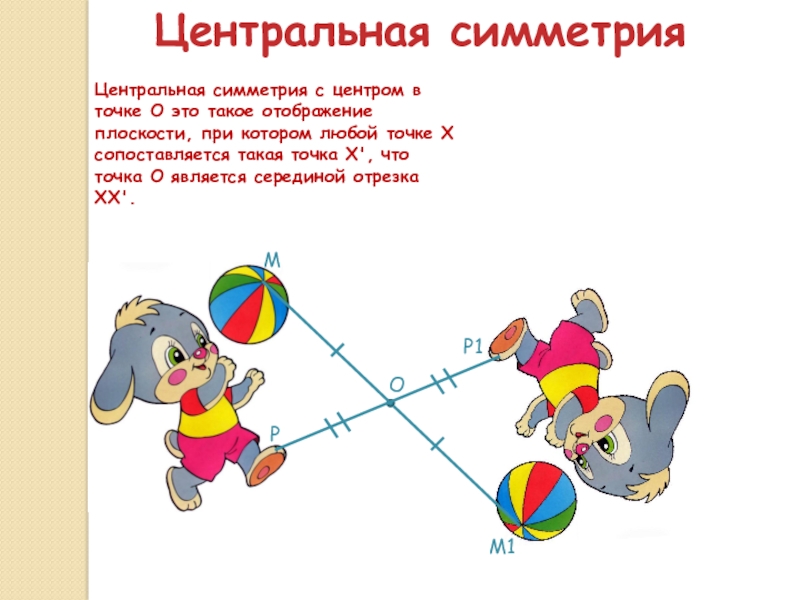
Слайд 5Центральная симметрия
Центральная симметрия с центром в точке O это такое отображение
плоскости, при котором любой точке X сопоставляется такая точка X', что точка O является серединой отрезка XX'.
О
М
М1
Р
Р1
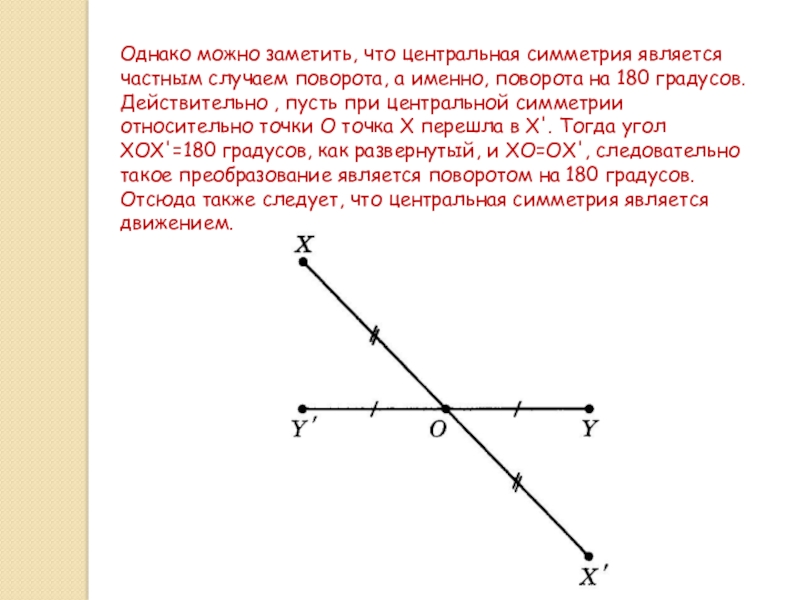
Слайд 6Однако можно заметить, что центральная симметрия является частным случаем поворота, а
именно, поворота на 180 градусов. Действительно , пусть при центральной симметрии относительно точки O точка X перешла в X'. Тогда угол XOX'=180 градусов, как развернутый, и XO=OX', следовательно такое преобразование является поворотом на 180 градусов. Отсюда также следует, что центральная симметрия является движением.
Слайд 7Буквы А, М, Т, Ш, Е имеют вертикальную ось симметрии. Буквы В,
З, К, С, Э, Е имеют горизонтальную ось симметрии..
А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии.
СИММЕТРИЯ В РУССКОМ ЯЗЫКЕ
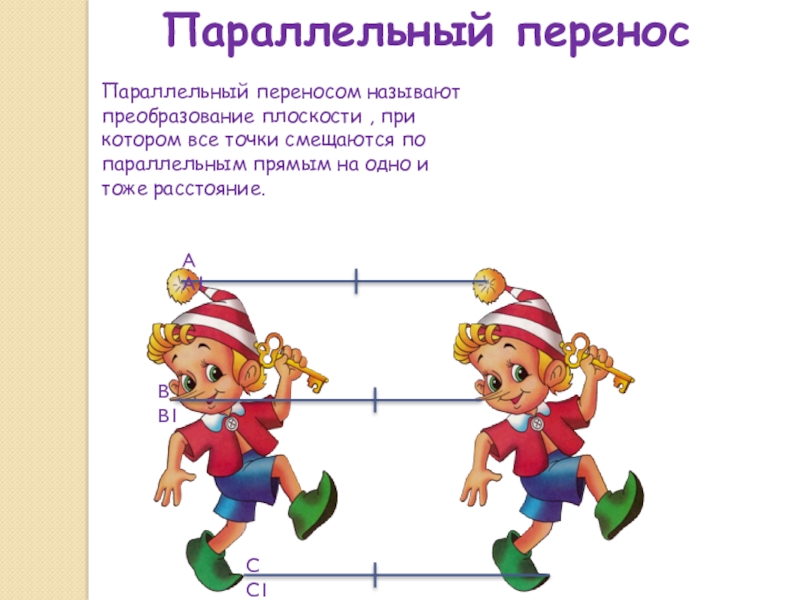
Слайд 8Параллельный перенос
Параллельный переносом называют преобразование плоскости , при котором все точки
смещаются по параллельным прямым на одно и тоже расстояние.
А А1
В В1
С С1
Слайд 9Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются
по параллельным (или совпадающим) прямым на одно и то же расстояние.
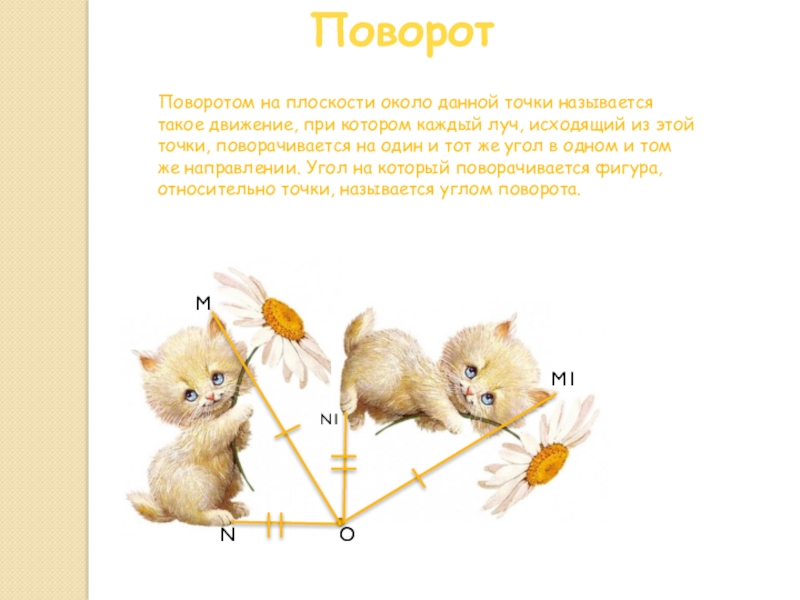
Слайд 10Поворот
Поворотом на плоскости около данной точки называется такое движение, при котором
каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Угол на который поворачивается фигура, относительно точки, называется углом поворота.
О
М
М1
N1
N
