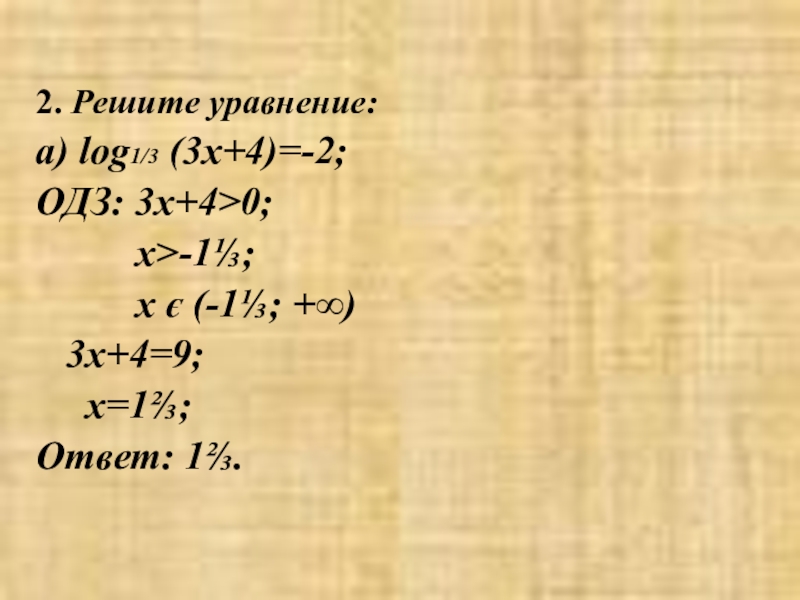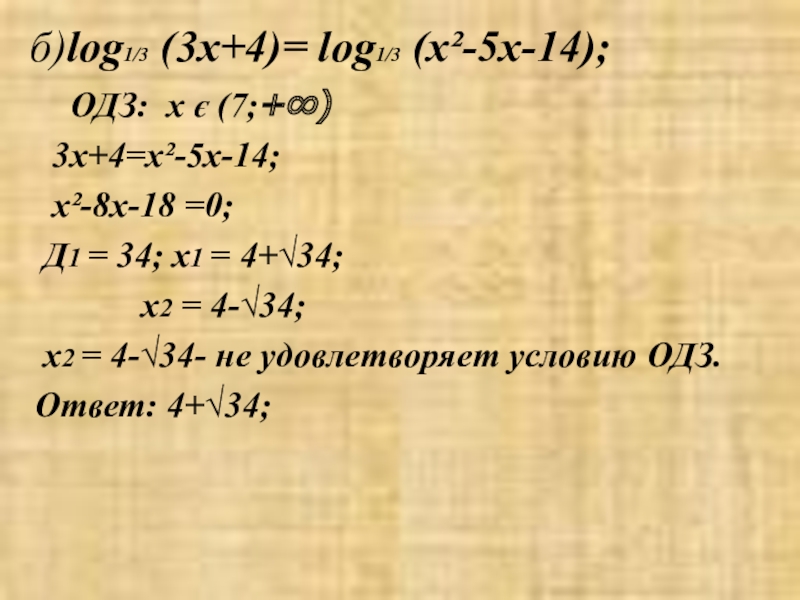ln x
log2 x log0/5 x log7 x
Логарифмы- это всё:
Музыка и звуки!
И без них никак нельзя
Обойтись в науке!
log1/8 x log6 x log2/3 x
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Обобщение и систематизация знаний по теме Логарифмическая функция. Логарифмические уравнения и неравенства
Содержание
- 1. Презентация к уроку Обобщение и систематизация знаний по теме Логарифмическая функция. Логарифмические уравнения и неравенства
- 2. Тема:
- 3. Слайд 3
- 4. Слайд 4
- 5. История возникновения логарифмов1614 год - Джон Непер
- 6. Джон Непер John Napier Дата рождения: 1550
- 7. Слайд 7
- 8. Проверка домашнего задания 1.Найти область определения функцииy=lg(x-1)
- 9. 2. Решите уравнение:а) log1/3 (3x+4)=-2; ОДЗ: 3х+4>0;
- 10. б)log1/3 (3x+4)= log1/3 (x²-5х-14);
- 11. 3. Решите неравенство:log0.9(x-4)≥ log0.9 (8-x) ОДЗ: х
- 12. Определение логарифма Логарифмом числа
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Сравните с единицей основание логарифма, если:
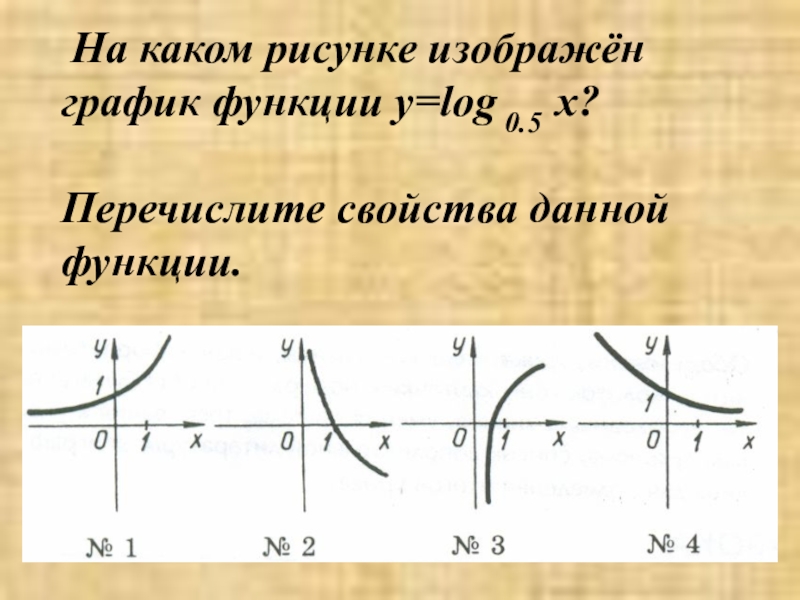
- 18. На каком рисунке изображён
- 19. 4.Какие из данных функций являются убывающими, а
- 20. Слайд 20
- 21. Слайд 21
- 22. Какие методы решения уравнений вам известны?- Решение
- 23. Решите
- 24. Физкультминутка
- 25. Слайд 25
- 26. Слайд 26
- 27. Ода логарифмической спиралиПотому-то, словно пена, Опадают наши
- 28. log3 x log1/5 x
- 29. ????? Путешествие на северо-восток Вопрос: Если
- 30. !!!!! Путешествие на северо-восток Ответ: Рано или
- 31. Уравнение логарифмической спирали Логарифмическая спираль описывается уравнением ,
- 32. Свойства логарифмической спирали Произвольный луч, выходящий из полюса
- 33. Свойства логарифмической спирали Логарифмическая спираль – кривая
- 34. Свойства логарифмической спирали Если вращать спираль вокруг
- 35. Свойства логарифмической спирали Если вращать спираль вокруг полюса против часовой стрелки, то можно наблюдать кажущееся сжатие спирали.
- 36. Знаменитости и спираль Впервые о
- 37. Слайд 37
- 38. “Логарифмы и ощущения”. Ощущения,
- 39. Слайд 39
- 40. Слайд 40
- 41. Логарифмическая спираль в природеАкулы прежде чем напасть
- 42. Логарифмическая спираль в природеНапример, раковины
- 43. Логарифмическая спираль в природеПо логарифмическим спиралям закручены
- 44. Логарифмическая спираль в природеХищные птицы кружат над
- 45. Логарифмическую спираль можно встретить и в архитектуре. Шуховская башня в Москве.
- 46. Логарифмические линии в природе
- 47. Слайд 47
- 48. Слайд 48
- 49. Спасибо за внимание!
Тема: Обобщение и систематизация знаний по теме «Логарифмическая функция. Логарифмические уравнения и неравенства»
Слайд 2
Тема: Обобщение и систематизация знаний
по теме «Логарифмическая функция. Логарифмические уравнения и неравенства»
Форма урока: Семинар-практикум
Учитель: Кущева М.Л.
Форма урока: Семинар-практикум
Учитель: Кущева М.Л.
Слайд 3 Цели урока:
- Обеспечить повторение,
обобщение и систематизацию знаний по теме;
- Способствовать формированию умений применять приёмы: сравнения, обобщения, выделения главного, перенос знаний в новую ситуацию, развитию математического кругозора;
- Создать условия для развития познавательного интереса учащихся;
- Воспитывать ответственность за качество и результаты выполняемой работы на уроке, математическую активность, общую культуру.
- Способствовать формированию умений применять приёмы: сравнения, обобщения, выделения главного, перенос знаний в новую ситуацию, развитию математического кругозора;
- Создать условия для развития познавательного интереса учащихся;
- Воспитывать ответственность за качество и результаты выполняемой работы на уроке, математическую активность, общую культуру.
Слайд 4 Задачи урока:
- Повторить теоретический
материал;
- Обратить особое внимание но ОДЗ при решении уравнений и неравенств;
- Систематизировать методы решения логарифмических уравнений и неравенств.
- Обратить особое внимание но ОДЗ при решении уравнений и неравенств;
- Систематизировать методы решения логарифмических уравнений и неравенств.
Слайд 5История возникновения логарифмов
1614 год - Джон Непер впервые пришёл
к идее логарифмических вычислений.
Термин “логарифм” означает
“искусственное число”;
1624 год - Генри Бригс создал таблицы
десятичных логарифмов;
1716 год - Леонтий Магницкий издал
семизначные логарифмические
таблицы.
Термин “логарифм” означает
“искусственное число”;
1624 год - Генри Бригс создал таблицы
десятичных логарифмов;
1716 год - Леонтий Магницкий издал
семизначные логарифмические
таблицы.
Слайд 6Джон Непер
John Napier
Дата рождения: 1550 год
Место рождения: замок Мерчистон
( предместье
Эдинбурга)
Дата смерти:4 апреля 1617
Место смерти: Эдинбург
Научная сфера: математика
Альма-матер: Сент-Эндрюсский
университет
Дата смерти:4 апреля 1617
Место смерти: Эдинбург
Научная сфера: математика
Альма-матер: Сент-Эндрюсский
университет
- изобретатель логарифмов
Слайд 8Проверка домашнего задания
1.Найти область определения функции
y=lg(x-1)
x-1>0
x>1
D(у): x є (1;+∞)
Слайд 92. Решите уравнение:
а) log1/3 (3x+4)=-2;
ОДЗ: 3х+4>0;
х>-1⅓;
х є (-1⅓; +∞)
3x+4=9;
х=1⅔;
Ответ: 1⅔.
х є (-1⅓; +∞)
3x+4=9;
х=1⅔;
Ответ: 1⅔.
Слайд 10 б)log1/3 (3x+4)= log1/3 (x²-5х-14);
ОДЗ: х
є (7;+∞)
3x+4=x²-5х-14;
x²-8х-18 =0;
Д1 = 34; х1 = 4+√34;
х2 = 4-√34;
х2 = 4-√34- не удовлетворяет условию ОДЗ.
Ответ: 4+√34;
3x+4=x²-5х-14;
x²-8х-18 =0;
Д1 = 34; х1 = 4+√34;
х2 = 4-√34;
х2 = 4-√34- не удовлетворяет условию ОДЗ.
Ответ: 4+√34;
Слайд 113. Решите неравенство:
log0.9(x-4)≥ log0.9 (8-x)
ОДЗ: х є (4;8)
x-4≤ 8-x;
x ≤6.
Учитывая ОДЗ, х є (4;6].
Ответ: х є (4;6].
Слайд 12 Определение логарифма
Логарифмом числа b по основанию а
называется показатель степени, в которую
нужно возвести основание а, чтобы получить число b.
(а>0, а≠1, b >0).
log а b = с , b = а с
Основное логарифмическое тождество:
а log а b = b
нужно возвести основание а, чтобы получить число b.
(а>0, а≠1, b >0).
log а b = с , b = а с
Основное логарифмическое тождество:
а log а b = b
Слайд 14 Устные упражнения
Найдите область определения функции:
а) y=log 2 x
б) y=log ¼ (x-3)
в) y=lg (2x+1)
г) y=log 5 (-x)
а) y=log 2 x
б) y=log ¼ (x-3)
в) y=lg (2x+1)
г) y=log 5 (-x)
Слайд 15
Вычислите:
а) log 5 125; б) log 1/2 8;
в) log √3 3; г) log 9 1/27 ;
д) log 2 16; е) log 1/9 1;
ж) log 2 ¼; з) log √5 √5.
а) log 5 125; б) log 1/2 8;
в) log √3 3; г) log 9 1/27 ;
д) log 2 16; е) log 1/9 1;
ж) log 2 ¼; з) log √5 √5.
Слайд 17 Сравните с единицей основание логарифма, если:
а)
log a 10 < log a 9
б) log a 1/2 >log a 1/ 3
б) log a 1/2 >log a 1/ 3
Слайд 18 На каком рисунке изображён график функции y=log 0.5 x? Перечислите свойства
данной функции.
Слайд 194.Какие из данных функций являются убывающими, а какие – возрастающими?
а) y=log
½ x
б) y=log 2 (x-1)
в) y=log 0.3 x
г) y=lg x
б) y=log 2 (x-1)
в) y=log 0.3 x
г) y=lg x
Слайд 20 Решите уравнения:
1. log 5
x=1; 2. ln x=1;
3. log 3 x=-1; 4. log x 16 =2;
5. log 0.5 x=3; 6. log x 5=0.5;
7. lg x=0; 8. log х 81=4;
3. log 3 x=-1; 4. log x 16 =2;
5. log 0.5 x=3; 6. log x 5=0.5;
7. lg x=0; 8. log х 81=4;
Слайд 22Какие методы решения уравнений вам известны?
- Решение уравнений по определению логарифма;
-
Решение уравнений с помощью различных свойств логарифмов;
- Решение уравнений методом подстановки;
- Решение уравнений методом потенцирования;
Решение уравнений методом логарифмирования;
- Решение уравнений графическим методом.
- Решение уравнений методом подстановки;
- Решение уравнений методом потенцирования;
Решение уравнений методом логарифмирования;
- Решение уравнений графическим методом.
Слайд 23 Решите уравнения:
1.logх (x²+4х-5) = 2;
2.
lg (3х-17) = lg (х+1);
3. log12 (х-3) + log12 (х-2) = 1;
4. log6 х =2log6 3 + 0.5log6 49 – log36 2;
5. log²2 (х-1) - log2 (х-1) -6 = 0;
3. log12 (х-3) + log12 (х-2) = 1;
4. log6 х =2log6 3 + 0.5log6 49 – log36 2;
5. log²2 (х-1) - log2 (х-1) -6 = 0;
Слайд 26 Решите неравенства:
1. log 2 (3-2x) ≤ log 2 13;
2. lg (x-1)- lg (2x-11) > lg2;
3. lоg²3 x - 3lоg3 x – 4 ≥0;
2. lg (x-1)- lg (2x-11) > lg2;
3. lоg²3 x - 3lоg3 x – 4 ≥0;
Слайд 27Ода логарифмической спирали
Потому-то, словно пена,
Опадают наши рифмы,
И величие степенно
Отступает
в логарифмы.
Борис Слуцкий
Слайд 28log3 x log1/5 x lg x
ln x
Применение логарифмов
«Логарифмическая спираль»
log3 x log1/5 x lg x ln x
Слайд 29?
?
?
?
?
Путешествие на северо-восток
Вопрос: Если идти все время на
северо-восток, то куда попадешь?
Обычно на этот вопрос отвечают так: обойду земной шар и вернусь в точку начала пути.
Но этот ответ неверен. Ведь идти на северо-восток - это значит постоянно увеличивать восточную долготу и северную широту, и вернуться в более южную точку мы не сможем.
Обычно на этот вопрос отвечают так: обойду земной шар и вернусь в точку начала пути.
Но этот ответ неверен. Ведь идти на северо-восток - это значит постоянно увеличивать восточную долготу и северную широту, и вернуться в более южную точку мы не сможем.
?
Слайд 30!
!
!
!
!
Путешествие на северо-восток
Ответ: Рано или поздно мы попадем на
северный полюс.
При этом путь, который мы пройдем, будет иметь вид логарифмической спирали.
На рисунке вы можете видеть этот путь так, как мы увидели бы его, смотря на земной шар со стороны северного полюса.
При этом путь, который мы пройдем, будет иметь вид логарифмической спирали.
На рисунке вы можете видеть этот путь так, как мы увидели бы его, смотря на земной шар со стороны северного полюса.
!
Слайд 31Уравнение логарифмической спирали
Логарифмическая спираль описывается уравнением ,
где r – расстояние от точки, вокруг которой закручивается спираль (ее называют полюсом), до произвольной точки на спирали, – угол поворота относительно полюса, а – постоянная.
Спираль называется логарифмической, т.к. логарифм расстояния (logar) возрастает пропорционально углу поворота .
Спираль называется логарифмической, т.к. логарифм расстояния (logar) возрастает пропорционально углу поворота .
Слайд 32Свойства логарифмической спирали
Произвольный луч, выходящий из полюса спирали, пересекает любой виток
спирали под одним и тем же углом.
Это свойство применяется в режущих ножах. Вращающиеся ножи имеют профиль, очерченный по логарифмической спирали
Это свойство применяется в режущих ножах. Вращающиеся ножи имеют профиль, очерченный по логарифмической спирали
Слайд 33 Свойства логарифмической спирали
Логарифмическая спираль – кривая с «твёрдым характером».Она не
изменяет своей природы при многих преобразованиях, к которым чувствительны другие кривые. Сжать или растянуть эту спираль относительно её полюса – то же самое, что повернуть ее на определенный угол.
Слайд 34 Свойства логарифмической спирали
Если вращать спираль вокруг полюса по часовой стрелке,
то можно наблюдать кажущееся растяжение спирали.
Слайд 35Свойства логарифмической спирали
Если вращать спираль вокруг полюса против часовой стрелки, то
можно наблюдать кажущееся сжатие спирали.
Слайд 36 Знаменитости и спираль
Впервые о логарифмической спирали говорится в
письме французского математика Рене Декарта в 1638 г.
Великий немецкий поэт Иоганн Вольфганг Гёте считал логарифмическую спираль математическим символом жизни.
Логарифмическая спираль так поразила математика Якоба Бернулли, что он завещал высечь её изображение на своём надгробном камне вместе с надписью на латинском «Изменённая, возрождаюсь прежней».
Слайд 38 “Логарифмы и ощущения”.
Ощущения, воспринимаемые органами чувств человека,
могут вызываться раздражениями, отличающимися друг от друга во много миллионов и даже миллиардов раз. Удары молота о скользкую плиту в сто раз громче, чем тихий шелест листьев, а яркость вольтовой дуги в триллионы раз превосходит яркость какой-нибудь звезды, едва видимой на ночном небе. Но никакие физиологические процессы не позволяют дать такого диапазона ощущений. Опыты показали, что организм как бы “логарифмирует” полученные им раздражения, т.е. величина ощущения приблизительно пропорциональна десятичному логарифму величины раздражения.
Как видим, логарифмы вторгаются и в область психологии.
Как видим, логарифмы вторгаются и в область психологии.
Слайд 41Логарифмическая спираль в природе
Акулы прежде чем напасть на свою жертву, описывают
вокруг неё кривую, похожую на логарифмическую спираль
Слайд 42 Логарифмическая спираль в природе
Например, раковины многих моллюсков закручены именно
по этой спирали, чтобы не сильно вытягиваться в длину.
Также логарифмическую спираль можно увидеть в рогах архара (горного козла).
В природе логарифмическая спираль встречается довольно часто.
Слайд 43Логарифмическая спираль в природе
По логарифмическим спиралям закручены многие галактики, в частности,
галактика, которой принадлежит Солнечная система.
В подсолнухе семечки расположены по дугам, очень близким к логарифмической спирали.
Слайд 44Логарифмическая спираль в природе
Хищные птицы кружат над добычей по логарифмической спирали.
Дело в том, что они лучше видят, если смотрят не прямо на добычу, а чуть в сторону.
Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали.
Слайд 46 Логарифмические линии в природе замечают не только математики,
но и художники. Например, этот вопрос чрезвычайно волновал Сальвадора Дали.
Его навязчивой идеей стала картина Вермеера «Кружевница», репродукция которой висела в кабинете его отца. Много лет спустя Сальвадор Дали попросил в Лувре разрешение написать копию с этой картины. Затем попросил киномеханика показать на экране репродукцию нарисованной копии. Он объяснил, что, пока не написал эту копию, в сущности, почти ничего не понимал в «Кружевнице», и ему понадобилось размышлять над этим вопросом целое лето, чтобы осознать, наконец, что он инстинктивно провёл на холсте строгие логарифмические кривые.
Его навязчивой идеей стала картина Вермеера «Кружевница», репродукция которой висела в кабинете его отца. Много лет спустя Сальвадор Дали попросил в Лувре разрешение написать копию с этой картины. Затем попросил киномеханика показать на экране репродукцию нарисованной копии. Он объяснил, что, пока не написал эту копию, в сущности, почти ничего не понимал в «Кружевнице», и ему понадобилось размышлять над этим вопросом целое лето, чтобы осознать, наконец, что он инстинктивно провёл на холсте строгие логарифмические кривые.
Слайд 47 Итог урока
Итак,
мы сегодня с вами решали логарифмические уравнения и неравенства.
Давайте обобщим: какие методы решения уравнений мы применяли?
Готовясь к ЕГЭ, никогда не думайте, что не справитесь с заданием, а, наоборот,- мысленно рисуйте себе картину успеха и тогда у вас всё получится!
Давайте обобщим: какие методы решения уравнений мы применяли?
Готовясь к ЕГЭ, никогда не думайте, что не справитесь с заданием, а, наоборот,- мысленно рисуйте себе картину успеха и тогда у вас всё получится!
Слайд 48 Домашнее задание: -
уч. Г.П. Бевз «Математика-11»,
стр.44, с/р №1;
- сб. А.Г.Мерзляк,стр.82,
к.р.№4(1-6);
- сб. А.М.Чекова, стр.143-146.
